基于调制光频梳的薄膜铌酸锂波导超连续谱研究

黄毅，吴侃，肖泽宇，李铁映，蔡明璐，陈建平

（上海交通大学 电子信息与电气工程学院 区域光纤通信与新型光通信系统国家重点实验室，上海 200240）

0 引言

光学频率梳是一种频率谱线间间隔均匀且相干的多波长激光源。最近光学频率梳在不同领域的应用在不断拓宽，例如可以应用在光谱学［1］、原子钟［2］、光通信［3］和微波光子学［4］等中。产生光学频率梳的方法一般有三种：1）基于锁模激光器产生固定重复频率的光频梳［5］，这种方法由于激光器性能限制，难以集成化［6］；2）基于克尔非线性，在片上的高Q值微环或微腔中产生光学频率梳［7-8］，该方案较难在微环或微腔内同时实现超宽谱（如覆盖倍频程）且具有较小梳齿间隔的光频梳；3）利用电光效应进行电光调制产生光频梳［9-10］，这种方法可以获得重频大范围可调的光频梳，但产生的光谱宽度通常有限。过去的电光调制往往是利用非集成的铌酸锂调制器，近年来薄膜铌酸锂调制器受到了广泛的关注，相比于非集成的铌酸锂调制器，薄膜铌酸锂调制器可以达到更低的半波电压（2～2.5 V）［11］，因此使用薄膜铌酸锂调制器可以达到更大的调制深度，从而产生更宽光谱的电光频梳。

另一方面，将飞秒脉冲输入高非线性的波导，经波导介质的非线性效应，可以得到超宽的光谱展宽，即超连续谱产生［12-13］。特别地，为了实现光频梳的自参考锁定，需要将光谱展宽到覆盖倍频程。同时还需要将输入光谱做倍频，利用倍频信号与超连续光谱在光谱上的拍频，来提取出所需的载波包络频率。实现倍频的传统方式是利用周期性极化的晶体或者直波导［14］。最近，在氮化硅波导与氮化铝波导中已经实现了覆盖倍频程的超连续光谱和二次谐波产生，但这两种材料的倍频效率都比较低，氮化硅χ(2)=0.5 pm/V［15］、氮化铝χ(2)=1 pm/V［16］，因此在这两种波导中产生超连续光谱和二次谐波所需的能量为纳焦耳量级。

铌酸锂材料因其有较强的线性电光效应和较强的二阶、三阶非线性一直以来都受到广泛关注。近年来，薄膜铌酸锂的出现更是将铌酸锂的研究推向了高峰。通过将光场局域在很小的薄膜铌酸锂波导内，电光效应和非线性效应都得到了大幅增强。目前已经有论文报道了基于薄膜铌酸锂的高速光调制器、二次谐波产生以及超连续谱产生［17-21］。

本文仿真研究了基于薄膜铌酸锂调制器的电光频梳和飞秒脉冲产生，并利用该飞秒脉冲在一段薄膜铌酸锂波导中实现覆盖倍频程的超连续谱产生和倍频信号产生。通过级联铌酸锂调制器进行电光调制，产生了一个180 fs 的超短脉冲。接着使用该脉冲作为输入源输入一段薄膜铌酸锂波导，当输入能量达到126.4 pJ时，波导内产生的超连续谱达到倍频程并与倍频信号重叠，可用于实现f～2f的自参考锁频。本文还对脉冲的参数优化进行了分析，提出了较优的参数选取方案。

1 系统与原理

仿真系统框图如图1（a），其中CW 为连续光激光器输入，经过铌酸锂强度调制器（Intensity Modulator，IM）和铌酸锂相位调制器（Phase Modulator， PM）输出得到电光梳，然后利用一段色散补偿光纤（Dispersion Compensate Fiber， DCF）对信号的时域进行压缩，得到窄脉宽的脉冲信号，最后将这个脉冲信号输入铌酸锂波导通过超连续展宽得到倍频程的宽带光谱，并同时在波导中实现倍频信号的产生。

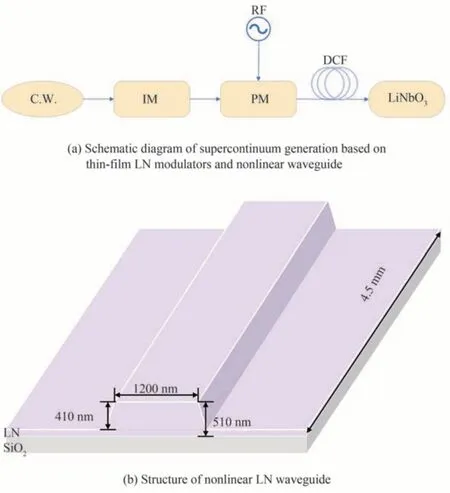
图1 仿真的实验设置图与薄膜铌酸锂波导的结构Fig.1 Setup and structure of thin film lithium niobate waveguide in simulation

对于通过级联调制器产生电光频梳和超短脉冲，已有较多文献研究。本文采用已有文献中的参数，即30 GHz 的调制频率下，单个铌酸锂相位调制器可以达到的最大调制深度为7.8π，其所需的射频功率为3.8 W［11］。图1（b）为仿真所用到的非线性铌酸锂波导示意。采用的是长为0.45 cm 的薄膜铌酸锂波导，铌酸锂波导厚为510 nm，刻蚀深度为410 nm，梯形波导的角度为75°，使用二氧化硅作为下包层，空气作为上包层，这样设计的波导在1 550 nm 附近的色散参数接近于零色散。

在铌酸锂波导中，需要考虑铌酸锂波导的χ(2)非线性和χ(3)非线性，因此利用非线性薛定谔方程对光场在薄膜铌酸锂波导中的传播演化进行数学建模［22-23］

式中，α为传播损耗，βn为n阶色散系数，ω0中心频率，c为真空中的光速，ε0为真空中介电常数，n0为中心波长处的折射率，表示光的自陡峭效应，τ=t−β1z为快变时间，PNL=ε0(χ( 2)E2+χ( 3)E3)为总的非线性极化。仿真中考虑了二阶和三阶非线性效应，高阶色散和光的自陡峭效应，并采用分步傅里叶算法对式（1）求解。为了验证仿真系统的可行性，采用文献［23］的参数进行仿真验证，图2（a）为输入脉冲在一段长为5 mm 的铌酸锂波导中传播时频谱的演化过程。输入的脉冲信号的能量为107 pJ，中心波长为1 560 nm，脉冲的脉宽为90 fs，重复频率为250 MHz。在频谱中，能观察到二次谐波信号出现在780 nm处，并且随着传播距离的变长，信号的频谱因其自相位调制效应逐渐展宽。在传输距离超过4 mm 后，在波长840 nm 附近出现了色散波。

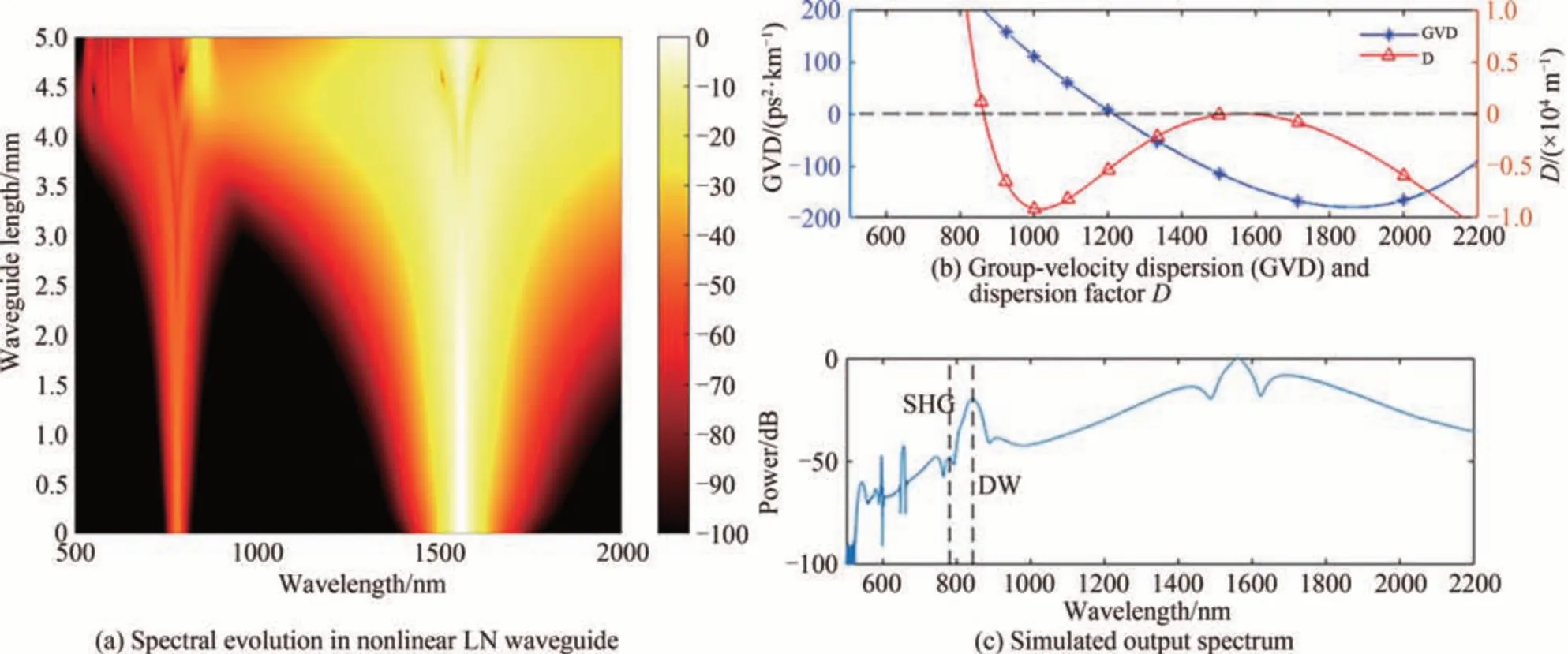
图2 光谱在铌酸锂波导中的演化过程和波导的色散参数以及波导输出的光谱Fig.2 Evolution of spectrum in lithium niobate waveguide， dispersion parameters of waveguide and output spectrum of waveguide

图2（b）为仿真中所用波导的群色散速度（Group Dispersion Velocity， GVD）和色散因子D在不同波长处的数值，其中色散因子［24］，其中心波长为1 560 nm。图2（c）为仿真中波导处的输出信号的频谱，其中色散波产生的位置所对应的是色散因子的零点的位置。仿真结果与文献［23］结果有着很好的一致性，证明了仿真系统的正确性。

2 仿真与分析

仿真系统中，主要考虑采用单频的连续光激光器作为输入源，选择30 GHz 作为射频调制频率，利用铌酸锂强度调制器产生初级梳，然后利用铌酸锂相位调制器调制得到电光频率梳。为了得到更大的调制深度与更窄的脉冲宽度，采用了级联多个相位调制器的设计。在级联相位调制器系统中，总的调制深度达到28π，经过色散补偿模块后，输出的脉冲信号的脉宽可以达到180 fs，其光谱的10 dB 带宽为5.5 THz，输出脉冲波形与光谱如图3。

图3 电光调制产生的时域波形和频谱Fig.3 Temporal waveform and spectrum based on electro-optic modulation

图4（a）为仿真中使用的铌酸锂的波导的群速度色散GVD（蓝色）和色散因子D（红色）。图4（b）是对应的仿真输出光谱，输入脉冲能量为126.4 pJ。在780 nm 附近，可以观察到二次谐波，同时在对应色散因子D为零的地方，可以发现与色散因子对应的色散波。在仿真中，研究并分析了铌酸锂波导在相等的脉冲宽度和不同的输入能量下对光谱的展宽作用，结果如图4（c），图中由上往下输入的脉冲能量依次由63.2 pJ 增大至126.4 pJ。当输入能量为63.2 pJ 时，能观察到中心频率处的光谱有了一定的展宽，在780 nm 处出现了与中心频率对应的二次谐波，并且在1 050 nm 处出现了一个色散波，其对应的是色散因子为零的波长。根据色散因子的定义，当只考虑二阶色散与三阶色散时，色散因子D可表示为

图4 仿真中波导的色散参数和在不同脉冲能量下的波导输出的光谱Fig.4 The dispersion parameters of the waveguide and the spectrum of the waveguide output at different pulse energies in the simulation

由于铌酸锂相位调制器的调制深度直接决定了压缩后光脉冲的脉宽，分别分析了调制深度为14π、21π和28π 的情况下，不同能量的输入脉冲在铌酸锂波导中的光谱演化。图5（a）展现了当调制深度为14π，脉冲信号脉宽为322 fs，10 dB 光谱宽度为2.89 THz 时，不同输入能量下的光谱演化图。其中从左往右输入脉冲的能量依次增加，当光谱产生超连续展宽时，所需的脉冲能量为1 102.2 pJ。图5（b）、（c）展示了调制深度为21π 与28π 时的光谱演化过程，此时输入铌酸锂波导的脉冲脉宽分别为230 fs 和180 fs，其得到的10 dB光谱宽度为4.1 THz 和5.5 THz，在这两种调制深度下，产生超连续展宽所需的脉冲能量分别为410.8 pJ 和126.4 pJ。

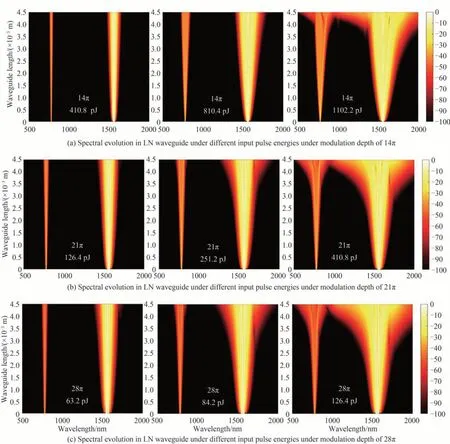
图5 不同输入能量、不同调制深度时，光谱在波导中的演化Fig.5 Spectral evolution in the LN waveguide under different input pulse energies， and different modulation depths

作为对比，还对调制深度为21π 与调制深度为28π 时光谱超连续展宽进行了分析。发现脉冲宽度越宽，即光谱的10 dB 带宽约窄，其产生超连续光谱所需的能量越高。调制深度为21π 时的电光梳光谱宽度大约为调制深度为28π 时的75%，其脉冲宽度约为调制深度为28π 的1.25 倍。但是经过同样一段波导后，要产生覆盖倍频程的超连续光谱，所需的能量却几乎为调制深度为28π 时的3 倍。因此，脉冲宽度或初始电光梳光谱的宽度，对超连续光谱展宽的影响比输入的脉冲的能量的影响更显著。

为了验证脉冲宽度与脉冲能量对光谱演化的影响，对不同调制深度下的演化情况进行了仿真分析。仿真参数与结果如表1，表中最右列为在当前的调制深度下，产生倍频程超连续谱所需的输入脉冲能量。图6为脉冲宽度与倍频程的超连续谱产生时所需能量的关系图。可以观察到，随着调脉冲脉宽的增加，超连续展宽所需的能量近似呈现平方变化。因此当脉冲宽度不断增加时，即光谱的带宽不断变窄时，在同样一段波导中，产生超连续所需要的能量会呈现近似平方的增加。

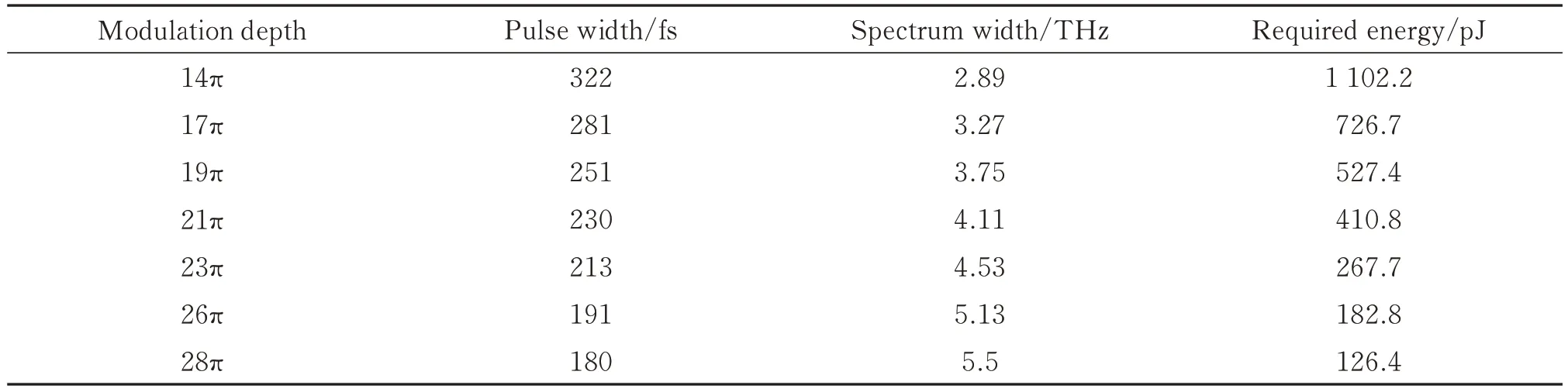
表1 不同调制深度时，产生倍频程超连续谱所需的脉冲能量Table 1 Required pulse energy to generate octave supercontinuum under difference modulation depth

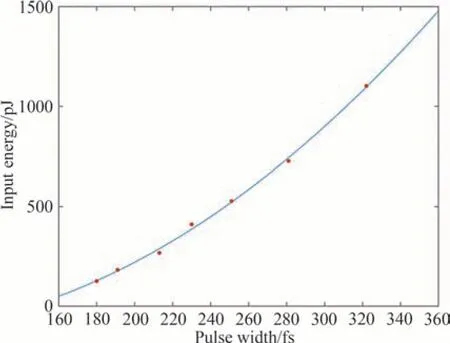
图6 脉冲宽度与产生倍频程超连续谱时输入能量Fig.6 The relationship of pulse width and input energy when supercontinuum spectrum of octave band generated

最后，在输入脉冲峰值功率固定的情况下探究了该系统对调制频率的调谐性的关系，结果如图7，图中展示了调制频率分别为20 GHz、25 GHz 与30 GHz，调制深度均为28π，脉冲的峰值功率均为700 W 时薄膜铌酸锂波导中的光谱的演化情况。因为调制频率的不同，电光调制产生的脉冲的脉宽也不同，在三种调制频率下的脉冲信号的脉宽分别为270 fs、220 fs 和180 fs，在这三种调制频率下，光谱产生倍频程超连续展宽所需要的波导距离是不同的。在20 GHz、25 GHz 和30 GHz 时产生倍频程的超连续展宽所用的波导长度分别为5.5 mm、5.2 mm 和4.5 mm。因此在相同的调制深度与输入脉冲的峰值功率下，随着调制频率的增加，输入信号光谱的非线性展宽效果就越好，产生覆盖倍频程的超连续谱展宽所需要的波导长度也就会更短。

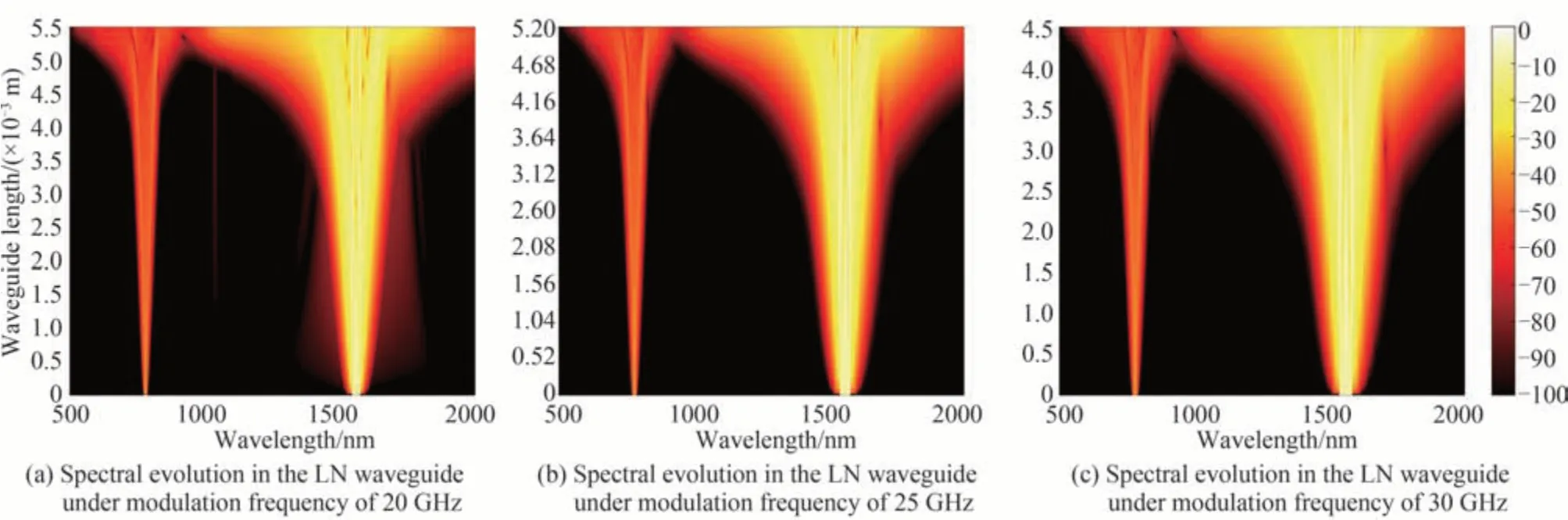
图7 不同调制频率时波导中光谱的演化过程Fig.7 Spectral evolution in the LN waveguide under different modulation frequencies

3 结论

本文仿真研究了基于薄膜铌酸锂调制器的电光频梳和飞秒脉冲产生，并利用该飞秒脉冲在一段薄膜铌酸锂波导中实现覆盖倍频程的超连续谱产生和倍频信号产生。利用对片上薄膜铌酸锂调制器的仿真，在30 GHz 的调制频率下，产生了180 fs 的电光调制信号，脉冲信号的能量为126.4 pJ，利用该信号在一段薄膜铌酸锂波导中产生了覆盖倍频程的超连续光谱。还探究了脉冲的脉宽与能量对覆盖倍频程的超连续谱产生的影响，并针对不同的脉冲脉宽提出在此脉宽下产生覆盖倍频程的超连续谱所需的能量，并分析了脉冲脉宽和能量在覆盖倍频程的超连续谱产生时的对应关系。最后，探究了在不同的调制频率下，薄膜铌酸锂波导中光谱演化的不同过程，为实现基于片上调制光梳在薄膜铌酸锂波导中产生倍频程的超连续光谱奠定了基础。