光纤离轴抛物面反射准直器的准直误差特性分析
唐靓,叶慧琪,郝志博,肖东,3
(1 中国科学院国家天文台南京天文光学技术研究所,南京 210042)(2 中国科学院天文光学技术重点实验室 南京天文光学技术研究所,南京 210042)(3 中国科学院大学,北京 100049)
0 引言
对于需要保持长期稳定的光学系统来说,采用光纤输入输出结构可以很好地将光路固化,实现可重复插拔工作,实现对仪器主体部分的高稳定环境控制。对于需要实现宽光谱波段工作的光谱系统来说,采用离轴抛物面(Off-Axis Parabolic,OAP)反射准直器对光纤端面输出光进行准直,由于其焦距不随入射光波长变化,可以在较大的波长跨度内实现无色差工作。然而实际情况下,光纤出射面并不完全等效于点源。不同光纤出射端面尺寸、远近场能量分布、定位误差情况均可能对出射光束的准直情况产生影响。从几何上来看,与透射式光纤准直器相比,反射式离轴抛物面准直器对于各类焦点定位误差的响应特性更为复杂。有研究人员对经离轴抛物面镜聚焦后的激光光斑进行了特性研究[1-2],发现此类反射镜对于入射角失准的敏感度极高,数毫弧度的偏斜即可导致焦面处峰值光强的大幅下降。也有研究人员对大孔径离轴抛物反射式准直仪的离轴量等参量和准直性能间的关系进行了研究[3],对理想情况和实际应用中需要考虑的干扰因素进行了讨论。
以高精度视向速度天文光谱定标用法布里-珀罗(Fabry-Perot,FP)定标源为代表的一些应用,对于照明角度能量分布具有高敏感性,同时又对照明稳定性有很高的要求。视向速度法通过对天体光谱中的特征吸收线波长位置随时间的变化进行测量,来了解其在视线方向上的运动情况,是进行系外行星探测的重要手段[4]。要实现宜居带内系外行星的探测,需要通过与高精度定标源进行实时同步对比等手段来实现米/秒级以上精度的视向速度探测[5]。基于法布里-珀罗标准具的宽光谱照明高精度法布里-珀罗定标源,具有覆盖光谱范围广、谱线分布均匀、可长期连续工作、可靠性高等优点,与钍氩灯等传统定标源配合使用,可显著提高高分辨率天文光谱仪的波长定标精度[6-9]。然而这要求定标源系统出射谱峰的自身稳定性能够维持在很高的水平(1 m/s 变化即对应于3.3×10−9谱线线心分数漂移)。面对高精度视向速度测量的宽工作波段、极高光谱稳定性挑战,需要对核心法布里-珀罗标准具腔体进行高稳定环境控制,这就要求在尽可能紧凑的尺寸限制下,实现无色差的高稳定光纤输入耦合和准直。基于离轴抛物面反射镜的反射式光纤准直器,结构紧凑、安装方便,可以实现无色差的光纤出射光准直,是用于此类宽波段法布里-珀罗天文光谱定标系统的理想输入结构。然而,目前为止,尚缺乏对光纤定位误差导致输入耦合准直偏差特性进行针对性研究的相关文献报道。
本文面向新型天文光谱定标用法布里-珀罗定标系统的应用需求,结合实验手段对输入光纤和离轴抛物面反射式光纤准直器进行联合建模,以对其准直效果和误差特性进行计算分析,结果将为不同光学系统应用下的OAP 准直器参数选择提供参考。
1 高精度法布里-珀罗定标源的照明敏感性
由于法布里-珀罗标准具的透射极大峰由多光束干涉形成,用作滤光器件,理想平行光入射时,不同的入射倾角对应于不同的干涉极大波长位置。而非理想平行光入射时,出射谱峰极大位置和谱线形状则与入射光束的角度能量分布相关[10]。因此,法布里-珀罗定标源系统的输入角度能量分布和角度稳定性对于其输出定标光的谱峰形状、分布和稳定度有显著影响[11],进而关系着能够实现的整体仪器定标精度。从实际的系统结构来看,输入光纤芯径及定位误差,以及所采用的准直器焦距等因素对于出射定标光的谱线分布情况有明显的影响。图1 比较了理想点源和实际光纤输入情况下,法布里-珀罗标准具透射谱峰的归一化曲线,可以看到相对理想曲线,实际的出射谱峰极大位置有所偏移,并且可能产生明显的展宽和偏斜。图2 展示了采用2.16 米望远镜高分辨率光纤光谱仪(High-Resolution Spectrograph,HRS)拍摄的三种不同耦合情况下同一法布里-珀罗标准具的透射光谱,图2 中,从上到下依次为较短准直焦距、较粗光纤,较短准直焦距、较细光纤,较长准直焦距,较粗光纤三种情况,可以看到谱线宽度和形态出现了明显的变化。
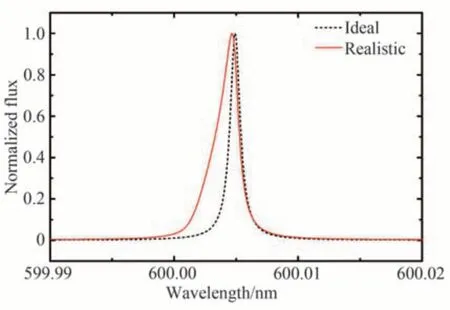
图1 法布里-珀罗标准具的理想(虚线)和实际(实线)透射谱峰Fig.1 The ideal (dotted line)and realistic (solid line)transmission peak of an FP Etalon

图2 2.16 米望远镜HRS 光谱仪拍摄的不同耦合情况下同一法布里-珀罗标准具的透射谱图Fig.2 Spectral images taken by the 2.16-HRS spectrograph of the same FP etalon under different illumination
不同种类和尺寸光纤的出射光远近场分布和稳定性有明显的差异,由此产生的准直误差将对出射定标光产生不可忽略的影响,有必要对其进行深入的分析研究。除了固定条件下的谱线宽度和形态外,光机系统的机械形变或蠕变引入的照明变化,将可能引入虚假的视向速度信号,因此还有必要对不同OAP 条件下的耦合照明变化引起出射角度能量分布变化的敏感程度进行研究。本文采用光线追迹法,对光纤输入OAP反射式准直器的准直特性进行深入分析,从而为OAP 光纤准直器在要求高精度、高稳定性的天文光谱定标系统中的应用提供参考。
2 仿真方法
2.1 光纤出射
不同光纤具有不同的出射特点,分析使用的光纤出射参数详见表1。分别拍摄相同数值孔径(Numerical Aperture,NA)入射情况下200 μm 芯径多模光纤(Multimode Fiber,MMF)、100 μm 芯径多模光纤和模场直径为4.2 μm 的单模光纤(Single-Mode Fiber,SMF)的近场和远场图像,对其能量分布进行分析计算,从而获得近场和远场径向能量分布情况。之后根据特定光纤的远近场分布曲线生成用于计算的初始入射网格。

表1 仿真分析中使用的光纤出射参数Table 1 Fiber output parameters used in the simulation
2.2 离轴抛物面反射
如图3 所示,O为原点,F为焦点,E、D、A、A′分别为主面和探测平面与y轴、主光轴的交点,OO为反射镜中心点。OAP 反射镜的抛物面方程可写为

图3 离轴抛物面反射准直器示意图Fig.3 Illustration of the off-axis parabolic reflective collimator
式中,fP为OAP 反射镜的母焦距(Parental Focal Length,PFL),与反射焦距(Reflective Focal Length,RFL)fR、离轴角θ存在关系
仿真中假设OAP 有效孔径足够大,所使用的具体参数列表详见表2。假设光线由RO(x0,y0,z0)点出射,其单位方向向量为rin(a,b,c),所在的直线方程可写为

表2 仿真分析中使用的离轴抛物面参数Table 2 Off-axis parabolic mirror parameters used in the simulation
通过式(1)和(3),可以求出光线在抛物面上的入/反射点坐标RP(xp,yp,zp)和反射单位向量rout(a′,b′,c′),从而获得出射光线在探测面处的位置坐标RD(xd,yd,zd)和单位向量rD(a′,b′,c′)。
2.3 光纤定位误差
在表征光纤定位误差时,首先假设存在如图4 所示的坐标关系,其中Off为光纤出射端面中心点,fff为出射光轴的指向单位向量,与zf轴重合。Rff为光纤端面上的出射点,rff为单位出射向量。光纤的定位误差通过绕zf轴、yf轴、xf轴的旋转误差(yaw,pitch,roll)和沿xf轴、yf、zf轴的位移误差(Δx,Δy,Δz)确定,所用的具体参数数值见表3。

表3 仿真分析中使用的光纤定位误差参数Table 3 Fiber positioning error parameters used in the simulation

图4 光纤定位示意图Fig.4 Illustration of fiber position
2.4 计算方法
所用仿真计算方法流程如图5 所示,首先根据所选的光纤参数和远、近场分布图获得远近场径向分布曲线,之后根据分布生成光纤输出格点数据,每个格点数据包括出射点坐标R(xf,yf,zf)、出射单位方向向量r(af,bf,cf)、出射光强I,其中出射光强的总积分值为100,代表总能量的100%。之后通过坐标变换,加入光纤定位误差,再将光纤坐标系中的入射网格格点位置坐标和方向向量坐标变换到OAP 坐标系内,形成抛物面入射格点数据。最后计算获得经OAP 反射镜反射后的出射光线角度和能量分布情况。
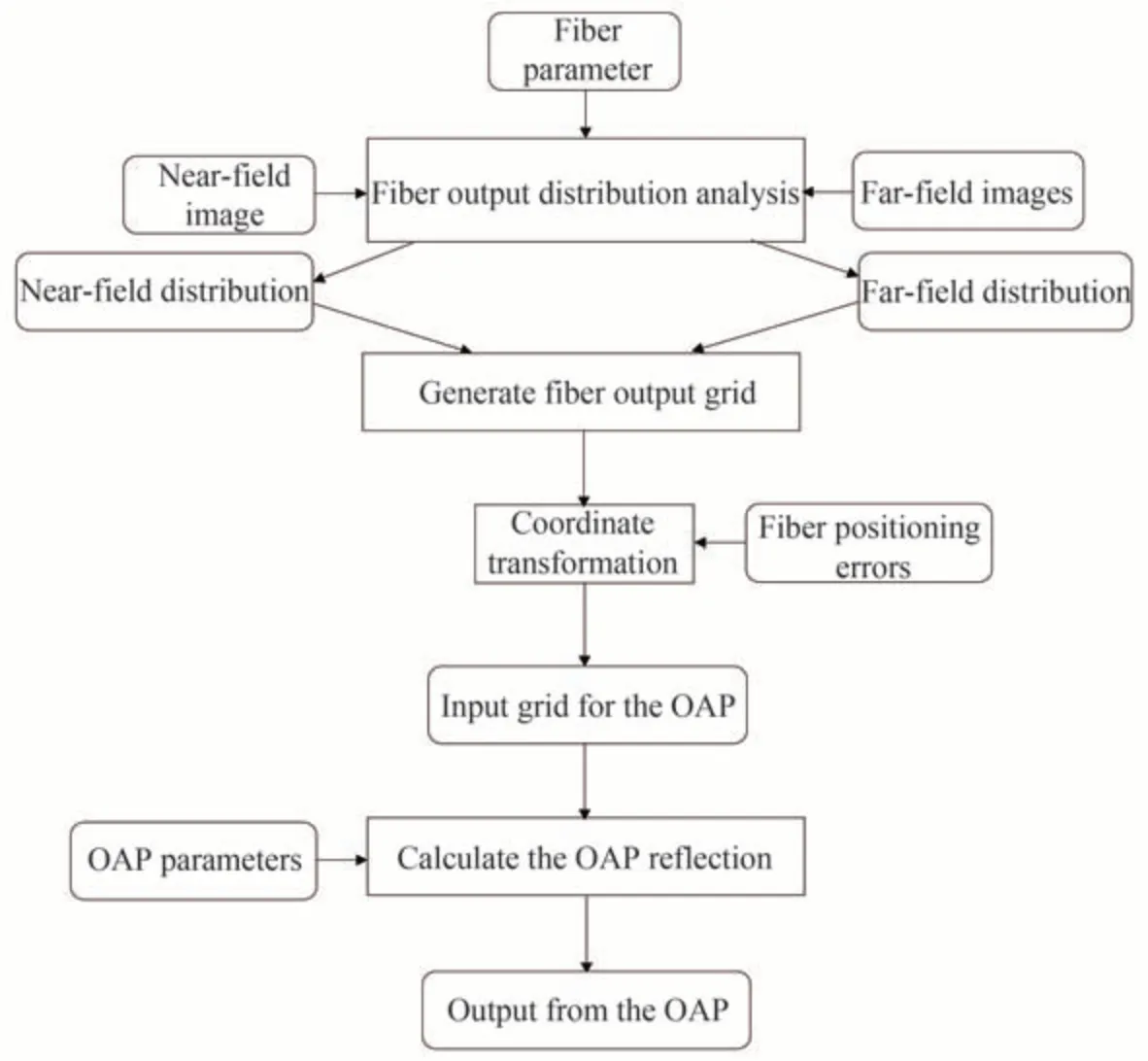
图5 仿真过程流程Fig.5 Flow chart of the simulation process
3 结果分析与讨论
3.1 光纤芯径及离轴抛物反射面参数对准直特性的影响
不同的输入光纤和反射镜参数均会对OAP 准直器的准直效果产生影响。为对比不同类型光纤经OAP准直器准直后的出射效果,首先对具有90°、45°、15°离轴角,16.5 mm 母焦距的光纤准直器,采用不同输入光纤,无任何定位误差时的出射场进行计算,结果如图6 所示。各子图中,上图为沿y轴观察时的出射光能量分布情况及角度质心位置的坐标(xbarycenter,zbarycenter),主要反映出射光束的中心指向;下图为以y轴为基准的出射光发散角能量分布统计图,以及能量加权平均后的发散角位置及角度标准差,主要反映出射光束能量的角度分布情况。可以看到,输入光纤的纤芯尺寸越粗,出射光的发散角越大,能量分布越分散,且峰值及平均能量位置向较大发散角处迁移;出射光束角度质心指向基本与y轴平行,随光纤纤芯的增粗,出射质心沿z轴正方向略有偏移,45°离轴角情况下,偏移最为明显。而同样的光纤输入下,相同的准直器抛物面母焦距,离轴角越小,准直效果越差,出射光束发散角范围越大,能量越向大发散角处偏移。
图7 比较了具有90°离轴角和与图6(a)~(c)相比更短(7.5 mm)、更长(25.4 mm)母焦距光纤准直器,以及与后者具备同样反射焦距(50.8 mm)的45°离轴角、43.4 mm 母焦距光纤准直器,无任何定位误差时的准直效果。结果显示,相同的90°离轴角情况下,母焦距越短,出射质心沿z轴正方向偏移越明显,偏移量与母焦距间存在关系。与此同时,出射光束发散角范围越大,能量越向大发散角处偏移,准直效果越差。同样的反射焦距下,大离轴角(90°)短母焦距(25.4 mm)情况下的出射质心沿z轴偏移,相对较小离轴角(45°)长母焦距(43.4 mm)情况下更为明显(纤芯直径200 μm 时前者约为1.89×10−3mrad,后者约为9.18×10−4mrad;纤芯直径100 μm 时前者约为4.75×10−4mrad,后者约为2.30×10−4mrad),即出射光束指向偏离光轴更为显著。相反地,大离轴角(90°)短母焦距(25.4 mm)情况下(加权平均发散角和标准差约为1.299 mrad 和0.468 mrad(200 μm 芯径),0.652 mrad 和0.235 mrad(100 μm 芯径)及2.07×10−2mrad 和8.88×10−3mrad(单模光纤))的出射光束能量角度分布相较小离轴角(45°)长母焦距(43.4 mm)情况下(加权平均发散角和标准差约为1.295 mrad 和0.460 mrad(200 μm 芯径),0.650 mrad 和0.230 mrad(100 μm 芯径)及2.06×10−2mrad 和8.81×10−3mrad(单模光纤))更为集中,准直效果相对更好。

图7 准确定位时OAP 准直器对应出射光角度能量分布情况(相同离轴角、不同母焦距以及不同离轴角、相同反射焦距)Fig.7 Angular energy distribution of the output beam without any fiber positioning error (OAP collimators with the same off-axis angle and different PFL, or different off-axis angle and the same RFL)
3.2 光纤旋转定位误差对准直特性的影响
上节分析了理想情况下,不同输入光纤芯径和反射面参数情况下OAP 反射准直器的准直效果。然而在实际应用中,无法完全保证光纤端面的准确定位。此时,各类光纤定位误差都可能对出射光束特性造成影响,进而对光学系统输出结果造成影响。
只存在旋转误差时,由于光纤绕光轴(zf轴)的对称特性,仅考虑绕yf轴和xf轴的旋转误差。为方便描述,以90°离轴角,16.5 mm 母焦距OAP 准直器为基准进行计算。图8、图9 展示了不同光纤绕yf轴或xf轴存在10 mrad 旋转误差的情况下,出射光的角度能量分布变化情况。各子图中,上图为沿y轴观察时的出射光能量分布情况及角度质心位置坐标;中图为以y轴为基准的出射光发散角能量分布统计图,以及能量加权平均后的发散角位置及角度标准差;下图则统计了相对无光纤定位误差情况下(即图6(a)~(c))出射光不同发散角区间内能量百分比变化,主要展示了引入光纤定位误差所导致的对应出射能量的角度分布转移变化情况,正结果代表此角度区间内能量分布上升,负结果代表区间内能量分布下降。
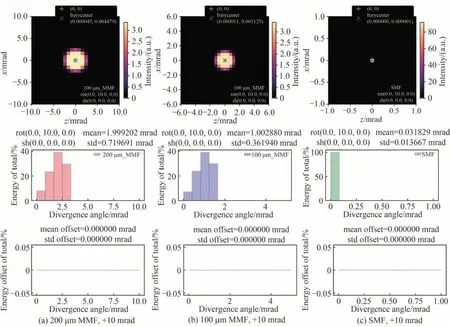
图8 ±10 mrad 绕yf轴旋转的光纤旋转误差(pitch)对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.8 Influence of ±10 mrad rotation fiber positioning error around the yf-axis (pitch)on the angular energy distribution of the output beam (OAP collimator with 90o off-axis angle, 16.5 mm PFL)
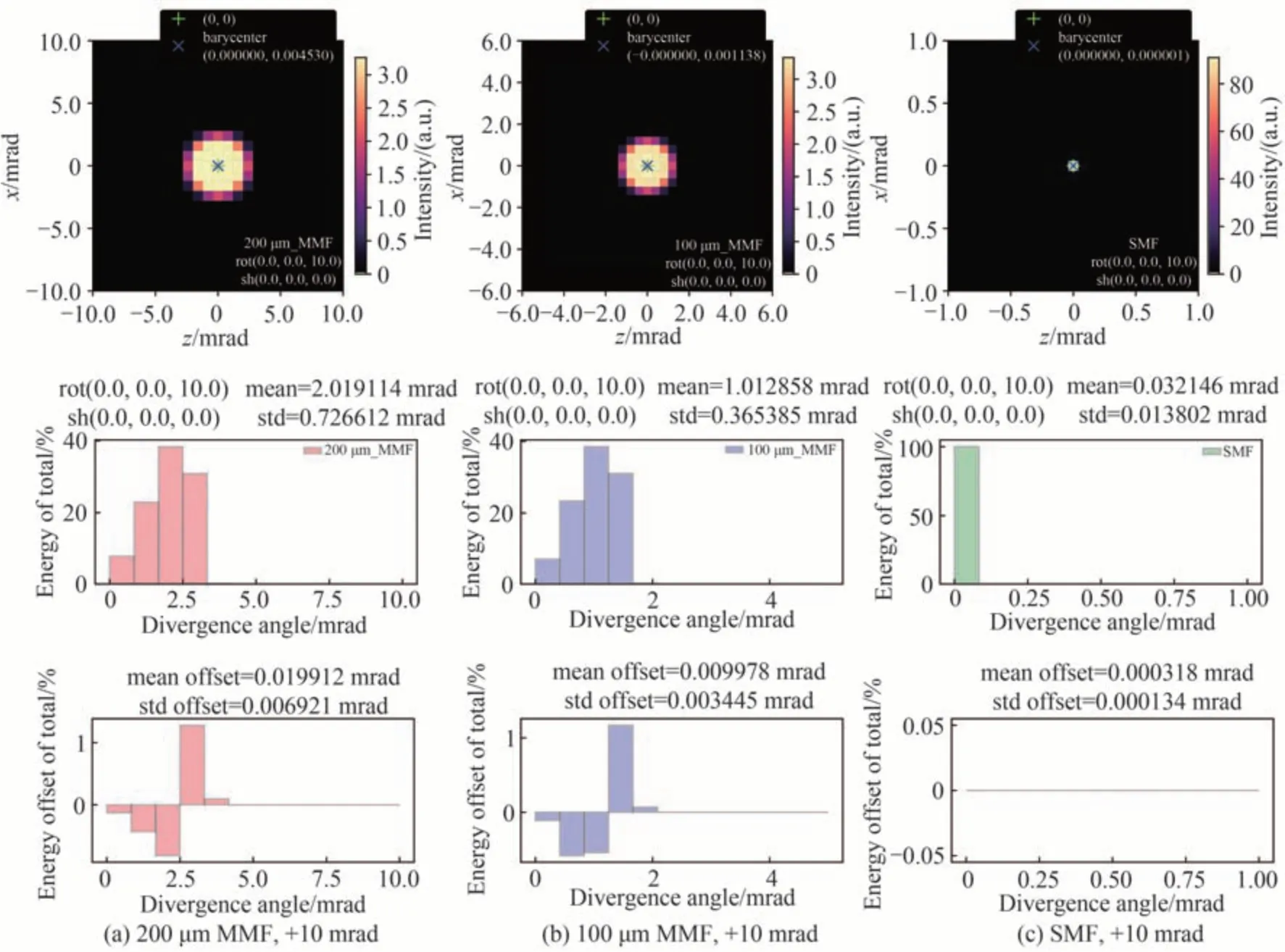
图9 ±10 mrad绕xf轴旋转的光纤旋转误差(roll)对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.9 Influence of ±10 mrad rotation fiber positioning error around the xf-axis (roll)on the angular energy distribution of the output beam (OAP collimator with 90o off-axis angle, 16.5 mm PFL)
图8 中可以看到,绕yf轴的旋转误差(pitch 误差)对出射角度能量统计分布和质心z坐标没有明显影响,会使出射光束质心沿x轴方向发生微小偏移。同样的pitch 误差下,光纤芯径越粗,偏移量越大(纤芯直径200 μm 时偏移量绝对值约为4.5×10−5mrad,100 μm 时约为1.1×10−5mrad,单模光纤时约为0),偏移量与pitch 误差符号相同,呈正相关。
图9 显示,绕xf轴的旋转误差(roll 误差)对质心x坐标没有明显影响,会使出射光束质心沿z轴方向发生微小偏移(纤芯直径200 μm 时偏移量绝对值约为5.15×10−5mrad,100 μm 时约为1.3×10−5mrad,单模光纤时约为0),偏移量同样与pitch 误差符号相同,呈正相关。另外可以发现,roll 误差对出射角度能量分布的影响相较同样幅度的pitch 误差更为显著,其加权平均角和角度标准差均与误差值呈正相关,即存在正误差时出射光束发散程度相对增大,存在负误差时出射光束发散程度相对减小。光纤纤芯尺寸越小,出射光束角度能量分布受旋转误差影响越小,单模光纤情况下受影响最小。10 mrad 绝对值的roll 误差下,纤芯直径200 μm时的加权平均发散角变化量绝对值约为1.99×10−2mrad,角度标准差变化量绝对值约为6.92×10−3mrad;纤芯直径100 μm 时分别为9.98×10−3mrad 和3.45×10−3mrad;单模光纤时则仅为3.18×10−4mrad 和1.34×10−4mrad。
3.3 光纤位移定位误差对准直特性的影响
图10、图11、图12 分别展示了只存在沿xf轴、yf轴、zf轴的10 μm 位移误差时不同光纤的出射光角度能量分布及变化情况。可以看到,位移误差对于出射光束的质心坐标和角度能量分布均有较明显的影响。

图10 ±10 μm 沿xf 轴平移的光纤位移误差(Δx)对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.10 Influence of ±10 μm shift fiber positioning error along the xf-axis( Δx)on the angular energy distribution of the output beam( OAP collimator with 90o off-axis angle, 16.5 mm PFL)

图11 ±10 μm 沿yf轴平移的光纤位移误差(Δy)对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.11 Influence of ±10 μm shift fiber positioning error along the yf-axis (Δy)on the angular energy distribution of the output beam (OAP collimator with 90o off-axis angle, 16.5 mm PFL)

图12 ±10 μm 沿zf轴平移的光纤位移误差(Δz)对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.12 Influence of ±10 μm shift fiber positioning error along the zf-axis (Δz)on the angular energy distribution of the output beam (OAP collimator with 90o off-axis angle, 16.5 mm PFL)
从出射光束的质心坐标来看,沿xf轴的Δx误差会造成质心x坐标偏移,偏移量与Δx呈负相关,即正误差导致负向偏移(所有光纤芯径下,偏移量绝对值均在约0.252 mrad 左右);对质心z坐标有较微弱影响,无论正负Δx,均使其发生沿z轴正方向的偏移(无论光纤芯径,均在约7.65×10−5mrad 左右)。沿yf轴的Δy误差,则对质心x坐标无明显影响;对出射光束质心z坐标有较明显影响,同样呈负相关关系,即正误差造成负向偏移(所有光纤芯径下,偏移量绝对值同样在约0.252 mrad 左右)。沿zf轴的Δz误差,对出射光束质心的x坐标无明显影响;会造成出射光束质心的z坐标的小量偏移,同样与误差呈负相关,且偏移量绝对值大小与光纤直径相关,纤芯直径100 μm 时最大(约3.05×10−3mrad),单模光纤时最小(约1.4×10−3mrad),纤芯直径200 μm 时介于两者之间(约2.41×10−3mrad)。
从出射光束的角度能量分布情况来看,无论Δx、Δy、Δz,无论正负,只要存在位移误差,就会导致出射光束发散程度增大,使得OAP 反射准直器准直效果变差。Δx、Δy误差对出射角度能量分布的影响要强于Δz。对于不同光纤来说,纤芯直径越细,其加权平均发散角对平移误差的敏感程度越高;相同的误差量下,单模光纤的平均发散角变化最大。单模光纤输入情况下,<10 μm 量级的Δx、Δy误差足以使出射光与无误差状态相比出现100%的能量角度转移。绝对值为10 μm 的Δx误差,出射光束的加权平均发散角增加量和角度标准差增加量分别可达到1.53×10−2mrad 和2.09×10−2mrad(200 μm 芯径),3.03×10−2mrad 和3.94×10−2mrad(100 μm 芯径),0.272 mrad 和1.48×10−2mrad(单模光纤)。正负Δy、Δz误差对出射角度能量分布的影响存在一定不对称性,光纤纤芯越粗不对称性越明显。+10 μm 的Δy误差导致的出射光束的加权平均发散角增加量和角度标准差增加量分别可达到1.44×10−2mrad 和1.96×10−2mrad(200 μm 芯径),2.99×10−2mrad 和3.88×10−2mrad(100 μm 芯径),0.272 mrad 和1.48×10−2mrad(单模光纤);−10 μm 的Δy误差导致的出射光束的加权平均发散角增加量和角度标准差增加量分别可达到1.62×10−2mrad 和2.21×10−2mrad(200 μm 芯径),3.08×10−2mrad 和3.99×10−2mrad(100 μm 芯径),0.272 mrad 和1.48×10−2mrad(单模光纤)。+10 μm的Δz误差导致的出射光束的加权平均发散角增加量和角度标准差增加量分别为1.38×10−4mrad 和9.8×10−5mrad(200 μm 芯径),3.63×10−4mrad 和2.61×10−4mrad(100 μm 芯径),4.51×10−3mrad 和3.81×10−3mrad(单模光纤);−10 μm 的Δz误差导致的出射光束的加权平均发散角增加量和角度标准差增加量分别为1.45×10−4mrad 和1.38×10−4mrad(200 μm 芯径),3.68×10−4mrad 和2.86×10−4mrad(100 μm 芯径),4.51×10−3mrad 和3.81×10−3mrad(单模光纤)。负Δy误差、负Δz误差引起的变化略强于正Δy误差、正Δz误差所引起的出射角度能量分布变化。
3.4 光纤组合定位误差对准直特性的影响
实际系统中,旋转误差和位移误差通常同时存在。图13、14、15 分布绘出了几种不同光纤旋转误差分别和Δx、Δy、Δz位移误差相组合下的角度能量分布和指向变化情况,各子图中上图为出射光束加权平均发散角变化情况,中上图为标准差变化情况,中下图为出射光束角度质心x坐标变化情况,下图为质心z坐标变化情况。可以看到,无论在何种位移误差基础上叠加pitch 误差,对出射光的角度能量分布变化规律的影响均不显著,但对于出射光束的质心指向变化规律有较明显的影响。相对地,在位移误差的基础上叠加roll 误差,则对出射光束指向变化规律无明显影响,而对其角度能量分布变化规律影响较大。
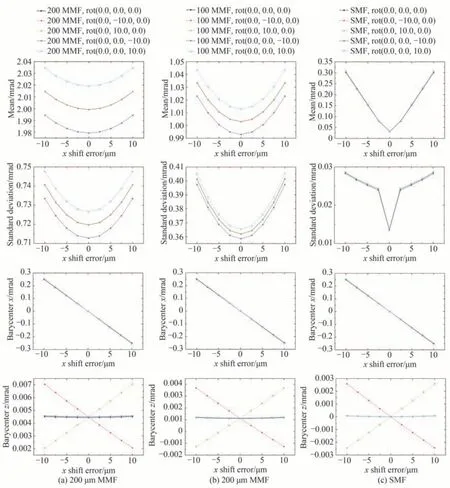
图13 光纤旋转与Δx 位移组合误差对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.13 Influence of rotation + Δx shift fiber positioning errors on the angular distribution of the output beam (OAP collimator with 90o off-axis angle, 16.5 mm PFL)
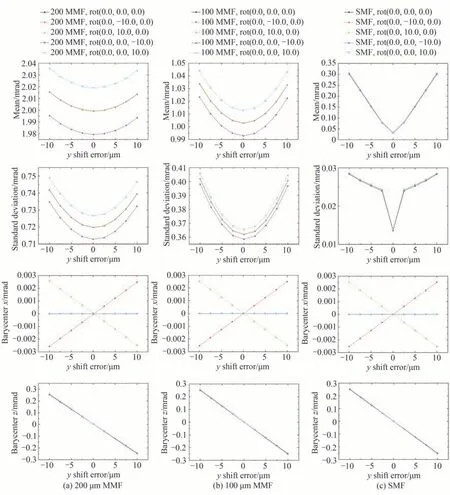
图14 光纤旋转与Δy 位移组合误差对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.14 Influence of rotation + Δy shift fiber positioning errors on the angular distribution of the output beam(OAP collimator with 90o off-axis angle, 16.5 mm PFL)

图15 光纤旋转与Δz 位移组合误差对出射光角度能量分布情况的影响(OAP 准直器离轴角90°,母焦距16.5 mm)Fig.15 Influence of rotation + Δz shift fiber positioning errors on the angular distribution of the output beam(OAP collimator with 90o off-axis angle, 16.5 mm PFL)
出射光束的加权平均发散角和标准差随位移误差的变化曲线基本以零位移误差点为底呈U 型,叠加正roll 误差时曲线发生向上偏移,而叠加负roll 误差时曲线发生向下偏移。纤芯直径越大,叠加偏移量越大。
从出射光束指向来看,质心x、z坐标随位移误差的变化曲线基本呈现线性关系。Δx位移误差叠加旋转误差时,质心x坐标与Δx位移误差变化呈负斜率关系,受pitch、roll 误差的叠加影响,斜率有不明显的微小变化。质心z坐标与Δx位移误差变化的关系则在叠加roll 误差时变化不大,基本维持水平直线状态;在叠加正pitch 误差时,质心z坐标与Δx位移误差变化关系将变为正斜率关系,在叠加负pitch 误差时,则变为负斜率关系。Δy位移误差叠加旋转误差时,质心z坐标与Δy位移误差变化呈负斜率关系,斜率在叠加的旋转误差作用下仅产生微小变化。质心x坐标与Δy位移误差变化的关系则在叠加roll 误差时变化不大,基本维持水平直线状态;在叠加正pitch 误差时,质心x坐标与Δy位移误差变化关系将变为负斜率关系,在叠加负pitch误差时,则变为正斜率关系。Δz位移误差叠加roll 旋转误差时,质心x坐标与Δz位移误差变化基本呈不变的水平直线关系,叠加正pitch 误差时变为正斜率关系,叠加负pitch 误差时则变为负斜率关系。质心x坐标与Δz位移误差变化则在叠加pitch 误差时维持与无旋转误差时相同的负斜率关系;这一斜率绝对值在叠加正roll 误差时有所增大,而在叠加负roll 误差时逐渐降低并向正斜率关系转变。
3.5 离轴抛物反射面参数对光纤定位误差敏感度的影响
由前文分析可以看到,OAP 光纤准直器的光纤定位相关准直误差相对光轴存在一定的不对称性,这是由OAP 本身的几何结构决定的,与其母焦距和离轴角存在一定对应关系。为进一步明确离轴抛物反射面参数对准直器的准直特性影响程度,表4 给出了具有相同反射焦距,但离轴角和母焦距不同的两种OAP 反射准直器在部分光纤定位误差组合情况下的出射光角度能量分布变化情况。可以看到,同样的光纤定位误差下,大离轴角(90°)、短母焦距(25.4 mm)情况下的出射质心变化小于小离轴角(45°)、长母焦距(43.4 mm)情况下的出射质心变化;而小离轴角、长母焦距情况下的出射角度能量分布变化则小于大离轴角、长母焦距情况下的出射角度能量分布变化。即:大离轴角、短母焦距情况下的OAP 反射准直器出射光束指向更稳定,小离轴角、长母焦距情况下的OAP 反射准直器出射光束的角度能量分布更稳定。
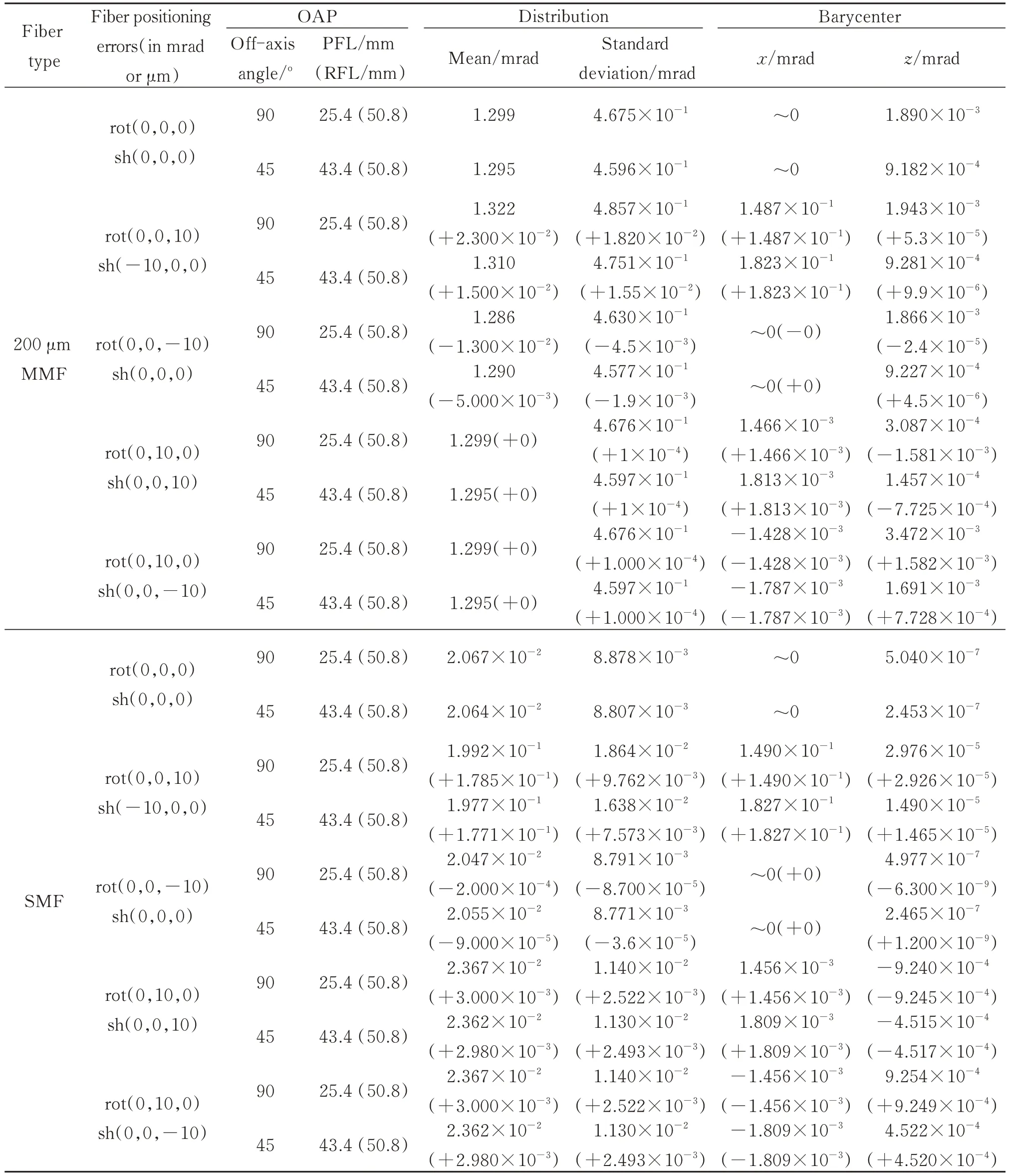
表4 相同反射焦距、不同离轴角和母焦距OAP 准直器部分光纤定位误差组合下的出射光角度能量分布变化情况Table 4 Angular energy distribution variation under different combinations of fiber positioning errors for OAP collimators with the same RFL, different off-axis angle and PFL
4 结论
本文对光纤种类及定位误差对于离轴抛物面光纤准直器准直效果的影响进行了仿真分析,主要可以得出以下几个结论:1)在不考虑光纤定位误差的情况下,OAP 准直器参数相同时,输入光纤纤芯直径越细,准直效果越好;2)在不考虑光纤定位误差的情况下,反射焦距相同时,在准直效果上大离轴角、短母焦距的OAP 准直器准直效果优于小离轴角、长母焦距的OAP 准直器;在出射光束指向偏离光轴的角度定位上,小离轴角、长母焦距的OAP 准直器定位准确度优于大离轴角、短母焦距的OAP 准直器;3)从准直效果来看,同样的OAP 准直器参数下,输入光纤纤径越粗,对旋转定位误差越敏感;输入光纤纤径越细,对位移定位误差越敏感;4)从出射光束指向来看,同样的OAP 准直器参数下,输入光纤纤径影响不大,主要受光纤端面定位误差的影响;5)反射焦距相同时,叠加同样的光纤定位误差,大离轴角、短母焦距情况下的OAP 反射准直器出射光束指向更稳定;小离轴角、长母焦距情况下的OAP 反射准直器出射光束的角度能量分布更稳定。
对于实际应用来说,还需要考虑系统的尺寸、通光孔径限制、加工和装配误差以及具体的应用需求。对于一些对出射光平行度和指向稳定度要求更高的应用来说,在反射焦距一定的情况下,应当尽可能采用大离轴角的OAP 准直器。而对于一些对出射光角度能量分布稳定性要求更高的应用来说,例如法布里-珀罗光谱定标系统,则应当在尺寸和结构允许的范围内,选择小离轴角、长母焦距的OAP 反射准直器,并且对光机结构的稳定性提出较高要求。

