星光成像的大气影响研究(Ⅲ):大气折射
陶志炜,戴聪明,武鹏飞,任益充,梅海平,冯云松,饶瑞中,魏合理
(1 中国科学院合肥物质科学研究院 安徽光学精密机械研究所 中国科学院大气光学重点实验室, 合肥 230031)(2 国防科学技术大学 电子对抗学院 红外与低温等离子体安徽省重点实验室, 合肥 230037)(3 先进激光技术安徽省实验室, 合肥 230037)(4 合肥工业大学 物理学院, 合肥 230601)
0 引言
人类利用恒星来进行导航,最早可追溯到古代人们通过北极星来确定方位。直到20 世纪50年代,星敏感器的横空出世,大大提升了恒星导航的精度。星敏感器是一种高精度的姿态敏感测量仪器,它通过成像系统对星空成像,测量恒星矢量在星敏感器坐标系中的分量,利用已知的恒星精确位置来确定载体相对于惯性坐标系的三轴姿态[1]。星敏感器导航技术的高精度、抗干扰性强、可不依赖其它系统进行独立导航等优点在近地空间各类机载、舰载、车载平台上有着广泛的应用[2]。
早期,星敏感器应用于卫星平台,承担了卫星姿态测量的任务,是卫星平台不可或缺的测量设备。由于大气层外可近似看成是真空环境,因此,星载星敏感器在工作时几乎不受大气的影响,其测姿精度通常可达到角秒级甚至亚角秒量级。随着空天观测平台的发展以及大气层内星敏感器观测高度的降低,大气对恒星探测的影响愈发显著,星敏感器在成像时不可避免的会受到地球大气背景辐射、湍流、折射等因素的影响。白天大气分子与气溶胶粒子会对太阳光产生散射,使得天空产生复杂的背景光,对星敏感器在白天观星时产生极大的干扰,严重降低成像的信噪比,使得恒星目标湮没在背景中,无法识别[3]。另一方面,大气分子与气溶胶粒子的存在会使得星光传输产生衰减,再加上大气本身存在折射率起伏,还会影响光波的相位,并对振幅产生调制,引发星光的闪烁和抖动[4-10]。由于大气折射率随高度存在一定变化,因此当星光经过大气传输时,大气折射会延长星光的传输路径,改变星光的传输方向,严重影响星光导航的精度。
为了定量评估大气对星光成像的影响,本系列文章Ⅰ、Ⅱ着重研究了背景辐射导致星光“看不见”以及大气湍流导致星光“看不准”这两个重要问题。为了进一步精确获取恒星的位置,采用星敏感器进行定位和导航,本文针对导致星光“看不准”中另一重要因素大气折射展开深入的研究。关于星光大气折射影响的研究最早可追溯到大气折射计算模型[11],该模型中大气折射使天体的表面位置向天顶移动。随后,国内外相关学者提出了众多模型用于星光大气折射的计算[12-18],并划分了几个使用不同星光折射计算方法的区域[19]:当观测天顶角小于70°时,计算仅需要温度,压力和湿度等参数便可获得较为不错的精度。当观测天顶角大于70°且在地平线的20°和5°之间时,温度梯度成为主导因素,计算需要使用文献[20]的方法,并使用标准大气的温度梯度和观测者的测量条件进行数值积分。当观测角度在更接近地平线的地方,需要在数值积分中使用局部温度梯度随高度变化的实际测量值进行计算。
本文是星光成像大气影响三部分研究(背景辐射、湍流及折射)的第三部分,目标在于选取最佳的星光折射计算数理模型,并针对我国幅员辽阔特点,选取典型地区,不断获取测试数据,优化完善我国典型区域星光折射的数据模型。首先,通过美国标准大气的温压数据,结合Ciddor 折射率模型,从计算精度、迭代次数以及计算速度三个方面对比分析了不同折射计算模型的优缺点,选取了最佳折射计算模型。其次,采用Ciddor 折射率模型计算得到的我国典型地区的折射率廓线数据,结合最佳折射计算模型,研究了星光折射引起的折射角、色散角、横向位移以及路径延长因子和延时等物理量的变化规律,并深入分析了输入参数不确定性对大气折射角计算的影响。本文的研究成果有望为实现星敏感器的准确观测,星光导航定位的精确校正提供理论和数据支撑。
1 理论模型
1.1 折射率模型
为了准确描述大气引起的折射和色散现象,建立准确的折射率模型是必要的。2014年,BARRELL H等比较了最常见的折射率模型,以评估光学设计软件Zemax OpticStudio 中的大气表面模型的准确性[21]。与此同时,作者还证实了OpticStudio 使用了Barrell&Sears 折射率模型[22]中的一个过时的方程式。与CIDOR P E 的最新工作相比[23],在I 波段(800~934 nm)和天顶角为30°的情况下,色散角可能存在0.8 mas 的差异。另一方面,若将Ciddor 模型与Birch&Downs 模型[24]和Bonsch&Potulski 模型[25]相对比,此时误差可能会缩小到0.2 mas 左右。本文选取Ciddor 模型作为计算折射率计算中最为精确的模型,因为其被国际大地测量学协会认为是计算大气折射率最为标准的方程[26]。除此之外,该模型对于本文的计算波段范围内的温度、湿度、压强都是准确的。其基本原理是假设大气折射率n与大气密度ρ存在Lorentz-Lorenz 关系,即[23,27],通过将n和ρ换算成一组参考条件,计算出感兴趣的大气条件的折射率。关于Ciddor 模型介绍读者请详见文献[23],这里不做过多的介绍。若考虑更长波段,例如中红外波段,或者OH和H2O 吸收线开始影响折射率变化的情况,这时采用Mathar 模型[28]可能是不错的选择,关于Mathar 模型的实际检验,可见SKEMER A J 等在中红外天空中的测试[29]。
1.2 折射计算模型
星光大气折射计算的精度不仅取决于折射率计算模型的精度,同时也依赖于折射计算模型的准确性。本节将构建星光成像大气折射影响的折射角和色散模型,大气折射角引起的横向位移模型以及路径延长模型等等。
1.2.1 折射角和色散
折射角和色散的计算依赖于模型几何和大气参数的选取。针对不同的模型几何,可将地球大气分为平面平行大气和球形大气。如图1 所示,平面平行大气通常是假设天顶角z0≈η。该模型仅对于z0→0 的情况下成立,随着z0的增大,折射角计算引起的误差也越大。平面平行大气条件下折射角和色散角的计算公式表示为[30]
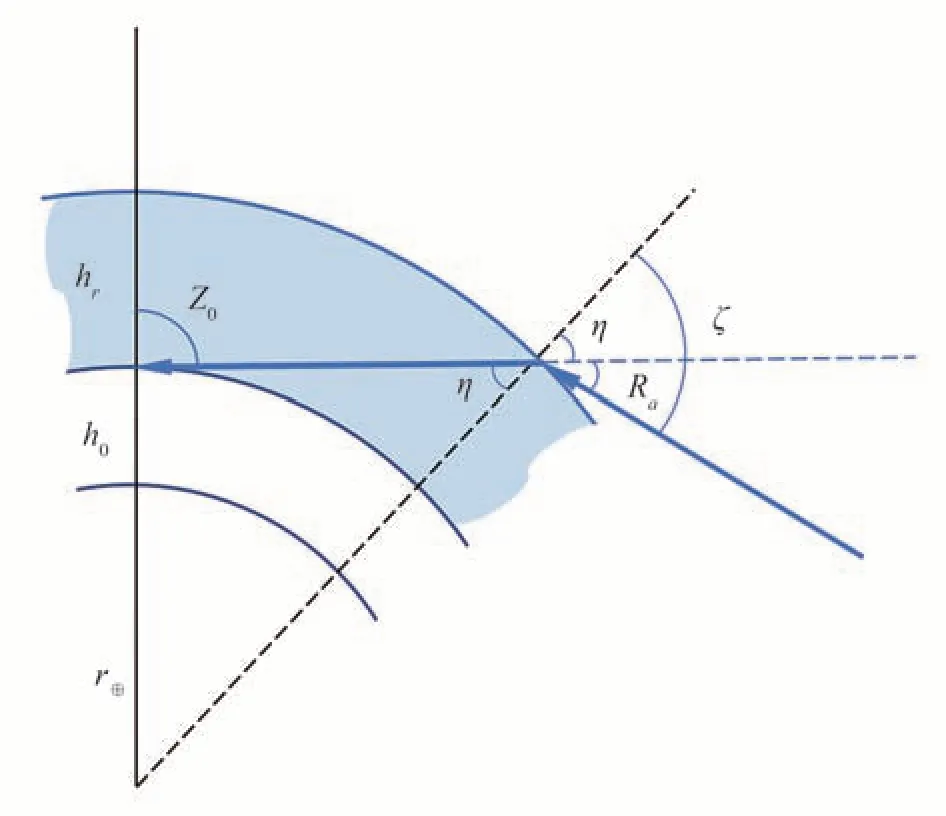
图1 各向同性球形整层大气折射示意图Fig.1 Diagram illustrating refraction in a homogeneous spherical whole-layer atmosphere
式中,ζ代表光线折射前的角度,n0代表对应观测高度的大气折射率,λ代表波长。值得注意的是,λ对于折射角和色散角的影响由折射率模型决定。针对球形大气,国内外学者提出众多模型和计算方法,例如Cassini模型[31],Corbard 误差函数模型[32-34],Mathar 气压指数模型[35],Oriani 定理[36]以及基于SLALIB 包的计算方法[37]等等,下面将主要介绍Cassini 模型(原因见模型精度小节中算法速度分析),其余模型详见附录。
当z0≈η不成立时,各向同性球形大气条件下折射角计算公式为
式中,r⊕代表折算地球半径,r⊕的大小由纬度和海拔高度共同决定(具体计算方法可参考文献[38,39]),hr则代表折算高度。在各向同性大气中,仅需要观测高度所对应的大气密度和压强数据便可计算出hr,表示[30]为
式中,p0和ρ0分别代表观测高度处对应的大气压强和密度,g代表重力加速度。若考虑等温大气,hr通常由式(4)决定[30]。
式中,kb代表Boltzmann 常数,T0代表观测高度对应处的温度,m代表空气分子的平均质量。
值得注意的是,上述介绍的折射角和色散计算模型无论对于哪种模型,都是将大气看成整层来进行处理,实际上,这种处理方法一定程度上会丧失计算精度,因此,下面我们介绍两种折射角计算方法,他们通常是将大气划分成若干层来进行计算的,其在计算速度上稍有欠缺(更多关于算法精度和速度的比较见下一小节)。一般而言,大气分层的个数是不确定的,一般以前后两次折射角的差值小于0.01″作为终止迭代的标准[40]。考虑到低层大气对于折射计算贡献较大,因此每层大气所对应高度一般采用式(5)进行计算[41]。
式中,ri代表每一层的厚度,t=i/N,i=1,2,…,N代表节点数,N代表总层数,r′⊕=r⊕+h0,h0代表观测高度,A=r′⊕sinz0。若假设划分为若干层后的大气每一层的折射率以及折射率梯度(等同于光线曲率)为常数,将计算方法划分为等折射率光线追迹法和等曲率光线追迹法[40]。对于等折射率光线追迹法而言,通常是假设光线是在每一层的边界处发生偏折,通过Snell 折射定律,特别地,对于第i层和第i+1 层,满足ni(hi+r⊕)sinθi=ni+1(hi+1+r⊕)sinθi+1,其中hi+1=hi+ri,如图2(a)所示,建立相邻两层的折射角度变化关系。当上述关系遍历所有层后,得到折射角计算公式[42]
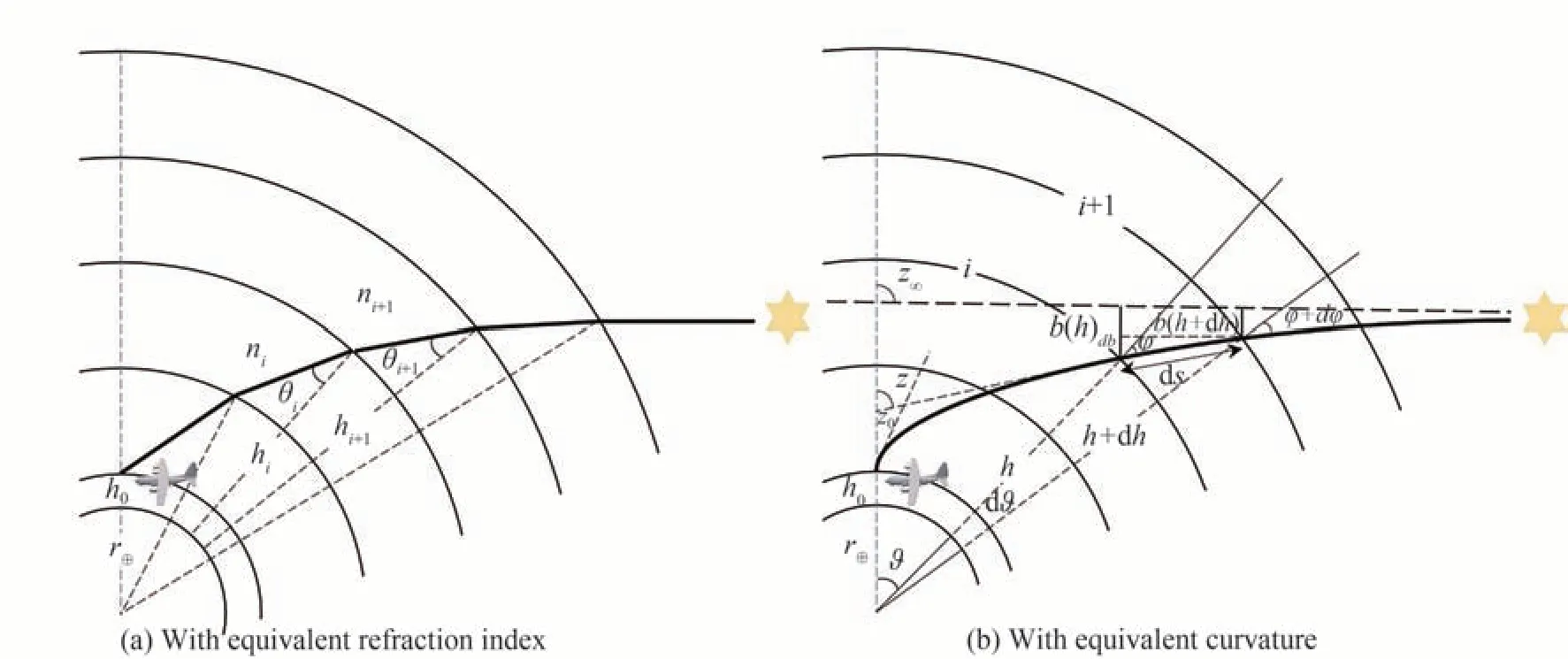
图2 球形多层大气折射示意图Fig.2 Diagram illustrating refraction in a spherical multiple-layer atmosphere
对于等曲率光线追迹法,通常是假设在每一层内折射率梯度为常数,即曲率半径在每一层的边界处发生变化,特别地,如图2(b)所示,对于第i层而言,曲率半径满足1/ki=−sinφidni/nidhi,其中ki代表第i层的曲率半径,φi代表光线沿第i层传播方向与该层半径矢量方向的夹角。一般地,曲率半径还可表示为微分方程[40,43]
除此之外,通过图2(b)中的几何关系,还可得到微分方程组[43]
式中,ϑ和dϑ的定义详见图2(b)。结合等式(7)和等式(8),通过图2(b)中的几何关系设置初值,使用四阶Runge-Kutta 法便求解上述一阶非线性微分方程组,得到光线发生折射前入射角度z∞。至此,等曲率光线追迹法计算得到的折射角可表述为
1.2.2 横向位移
上节我们通过求解微分方程组获得了光线经过大气折射后所产生的折射角和色散角。一般地,若要通过星敏感器确定恒星位置,通常可以通过恒星视在位置和真实位置所产生的折射角进行弥补。进一步,若要通过星敏感器确定大气中其他目标时,特别地当目标位置处于地球表面和低仰角时,若此时按原有方法计算其位置便会产生一定的误差,使得定位的精度产生偏差,因此有必要计算该误差,以弥补和精准确定目标所在位置[43]。以光线入射到大气层前的方向为基准,当目标位于一定高度时,真实光线方向与折射前光线方向存在一定的距离偏差,我们将此位移称为横向位移b,如图2(b)所示。通过图中的几何关系可得到微分方程[43]
结合式(7)、式(8)和式(9),通过图2(b)中的几何关系设置初值,其中ϑ∞,φ∞代表根据上小节设置的初值求解得到的大气最外层的ϑ,φ,使用四阶Runge-Kutta 法便可求解上述一阶非线性微分方程组,得到任意观测高度的横向位移b(∞)(h0)。
1.2.3 路径延长因子和路径延时
如图2 所示,星光经过大气传输后光线会因大气折射现象发生弯曲,延长了星光的传输路径,造成一定程度的路径延时[44]。本小节将通过等折射率光线追迹法构建星光传输的几何模型,计算星光经大气传输后的实际路径长度,给出大气折射引起的路径延长因子的计算公式。如图3 所示,大气按照式(5)被划分为若干层,以星光真实位置点S为起点,观测者位置O为终点连线,两者之间的距离代表星光的斜程距离,可通过式(11)得到。
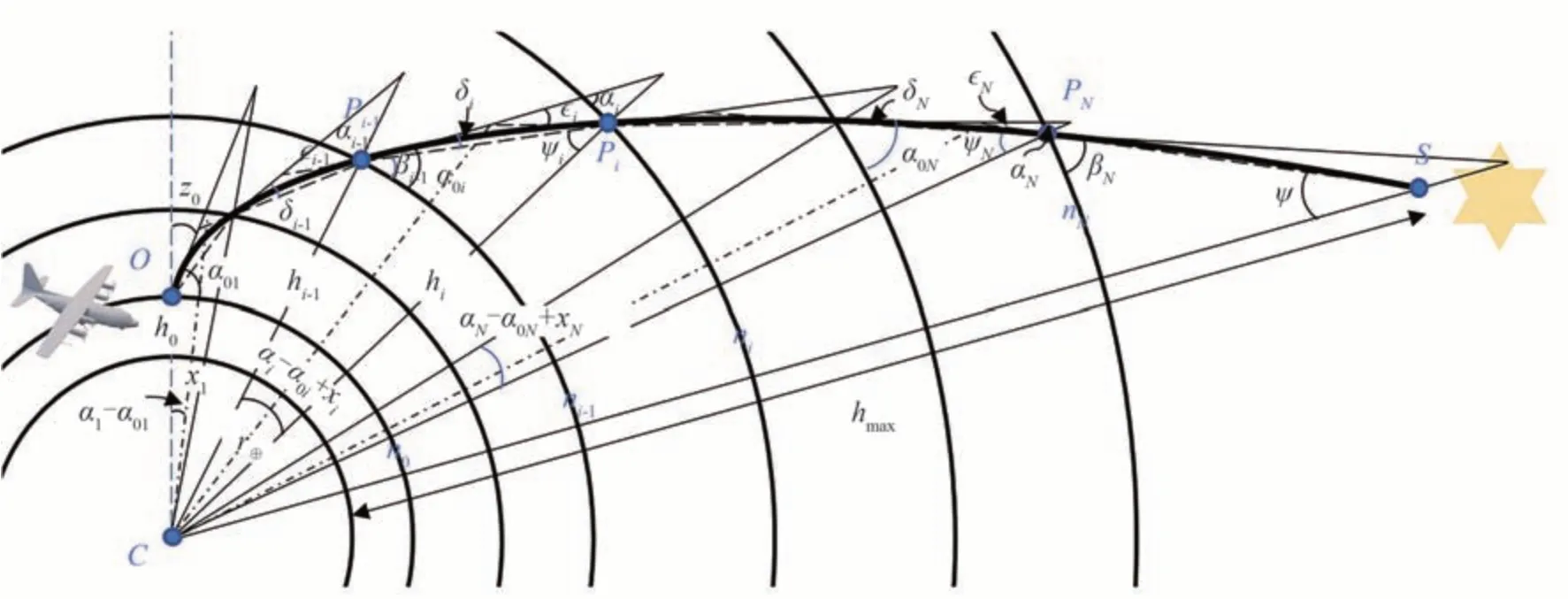
图3 大气折射引起的星光路径延长示意图Fig.3 Diagram illustrating the elongation of the optical ray trajectory caused by atmospheric refraction
根据图3 中给出的几何关系并结合正弦定律、Snell 折射定律,可得到
式中,Ci和Cmax表示为
δi和δN表示为
ϵi代表第i−1 层大气到第i层之间的折射角,根据直接积分法,ϵi可近似解析表示为[45]
结合式(12)、(15),对图3 中的三角形△CPi−1Pi,△CPN S使用余弦定律可得大气每一层的光线路径长度
根据式(16)、(17)可计算出光线经大气传输后的实际路径长度为,因此,星光经过大气折射后所产生路径延长因子和路径延时分别可表示为
式中,c代表光速,c=299 792 458.0 m/s。
1.3 模型精度
1.3.1 美国标准大气
地球的大气层可以看作是一个球状分层的介质,在不同高度层上有特定的折射率值分布。为了获得Ciddor 模型下的折射率分布并通过该分布对比不同折射计算模型的精度,首先使用美国标准大气模型进行计算。一般来说,美国标准大气是一个理想化的稳定状态的代表,它给出了大气压强、温度和其他参数随高度的变化情况,其中最大高度可达1 000 km[44]。美国标准大气假设温度随高度是满足线性分布的,而压强随高度的变化可以通过气体定律和流体静力学方程中获得[46],图4(a)、(b)给出了美国标准大气0~86 km 情况下的温度廓线和压强廓线,根据Ciddor 模型,可计算得到美国标准大气折射率(图4(c))及折射率梯度(图4(d))随高度的变化曲线。根据上节的大气折射计算模型,计算得到美国标准大气下不同模型的折射角随天顶角的变化情况,从图4(e)可以看到折射角总体是随着天顶角的增大而不断变大,当观测仰角较小时,此时大气折射的影响最为显著。需要指出的是,不同模型计算的折射角差异在图中并不显著,不同模型的计算精度需放大对比。最后,图4(f)和(g)还计算了美国标准大气下星光经大气产生的横向位移、路径延长因子和路径延时,这都为计算我国典型地区不同时间段所对应的大气折射参数提供了参考。
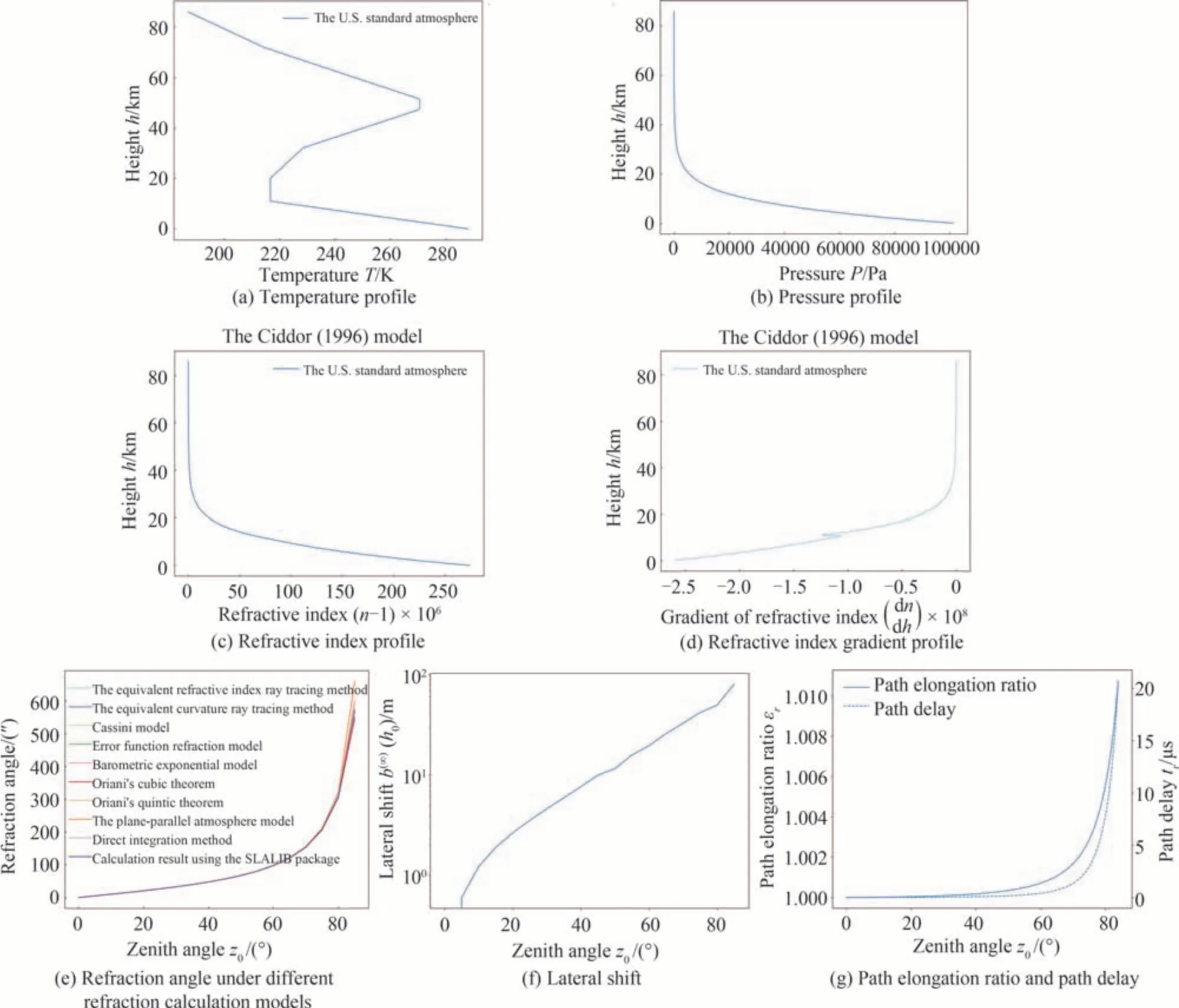
图4 美国标准大气下的大气参数廓线和折射计算结果Fig.4 Atmospheric parameter profiles and refraction calculations in the U.S.standard atmosphere
1.3.2 计算精度
图5 是不同折射计算模型计算的折射角(包括等折射率光线追迹法、等曲率光线追迹法、Cassini 模型、Corbard 误差函数模型、Mathar 气压指数模型、Oriani 定理、平面平行大气模型以及基于SLALIB 包计算结果)与直接积分法[31,45,47]计算结果偏差随天顶角的变化情况。这里以直接积分法作为基准进行比较是因为在美国标准大气下使用直接积分法获得折射角可近似替代Pulkovo 折射表[48]给出的折射角的标准值[49]。当越小,说明此时采用的折射计算模型与标准值越接近。如图5 所示,平面平行大气模型计算得到的折射角与标准值相差最大,说明使用该模型计算折射角和色散所产生的误差也最大。除此之外,还可以看出当天顶角较小时,使用Oriani 三次方定理和五次方定理计算得到折射角与标准值相差最小,此时选取Oriani 定理计算星光经大气所产生的折射角最为准确。另外,相比于Oriani 定理, 天顶角较小时Cassini 模型和等折射率光线追迹法计算结果也表现出较为精确的结果。当天顶角位于45∘附近时,使用Cassini 模型计算得到的结果最为精确,此时,与Oriani三次方定理相比,五次方定理表现出明显的优势。然而,当天顶角不断增大时,这时使用Oriani 定理计算大气折射角将较Cassini 模型和等折射率光线追迹法产生较大的误差。与Cassini模型相比,虽然在大天顶角时使用等曲率光线追迹法、Corbard 误差函数模型以及SLALIB 包计算将取得更为精准的计算结果,但其上述三种模型在天顶角较小将引入较大的计算误差。综上所述,若选取等折射率光线追迹法和Cassini模型来计算星光大气折射所产生的折射角和色散角,可获得较为不错的计算精度。

图5 美国标准大气下不同折射模型计算的折射角与直接积分法计算结果的偏差随天顶角的变化曲线Fig.5 The deviation of the refraction angle calculated by different refraction models and the direct integration as a function of zenith angle in the U.S.standard atmosphere
1.3.3 迭代次数
为了进一步从迭代次数角度对比多层大气折射计算模型(等折射率光线追迹法和等曲率光线追迹法)之间的区别,图6 给出了在天顶角为85°情况下使用的等折射率、等曲率光线追迹法计算的折射角随大气层数的变化情况(这里选取85°进行计算,是因为在美国标准大气下根据这两种大气折射计算模型得到折射角与标准值误差基本一致,因此排除了计算误差的影响)。需要说明的是,图6 的计算是在假设hmax= 86 km 的基础上进行的,由式(7)和(8)可以看出,若要使用等曲率光线追迹法求解折射角和色散角,通常需要折射率和折射率梯度曲线随高度变化的函数关系的。为此,尽管本文的验证计算只使用了86 km 以下的大气作为折射影响的主要因素,但在等曲率光线追迹法的计算当中仍使用美国标准大气下1 000 km 以下的数据作为生成n(h)和dn( )h/dh函数的来源。从图6(a)中可以看出,随着大气层数的不断增大,使用两种多层大气折射计算得到折射角逐渐趋于常数,相比于等折射率光线追迹法,等曲率光线追迹法收敛的速度较快。与等折射率光线追迹法不同的是,当大气层数较小时,等折射率计算结果随着层数的增大单调递增,而等曲率法计算结果却出现明显的振荡,这可能是由于数值求解微分方程组带来的计算误差导致的。若考虑两者的迭代误差,如图6(b)所示,等曲率法较等折射率法而言,在大气层数较小时,其迭代误差就基本趋向于0,说明等曲率光线追迹法在迭代次数方面较等折射率法表现出明显的优势。然而,值得说明的是,等曲率光线追迹法依赖折射率梯度的精度,需要超过最大观测高度以上的折射率和折射率梯度的数据(通常采用指数拟合,但会影响折射角计算的精度,最好有实测数据),另一方面,等曲率光线追迹法在处理实测数据时,需要对观测高度以下的折射率梯度数据进行分段平均,这时采用的平均方法(分段平均,滑动平均)也将很大程度决定折射计算的精度,但好处是相对于等折射率光线追迹法而言,大气分层个数较少,需要的迭代次数也较少。总体来看,如图5 所示,两种算法计算精度基本接近,尽管等曲率光线追迹法需要较少的大气分层便能获得不错的结果,但由于其不确定性因素较多且计算较为复杂,因此采用等折射率光线追迹法进行计算依然是最佳的选择。
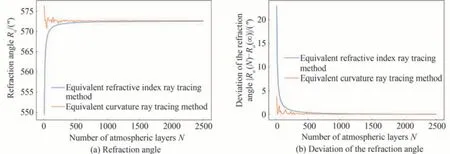
图6 等折射率、等曲率光线追迹法计算的折射角随大气层数的变化曲线Fig.6 The variation curve of refraction angle as a function of the number of atmospheric layers, which is calculated by the method of the equivalent refractive index ray tracing and the equivalent curvature one
1.3.4 算法速度
第一小节从计算精度的角度对比了不同整层大气折射模型和多层大气折射模型的计算精度,然而面对多经纬度、多时段、多个观测仰角情况下折射和色散计算的应用场景时,选取一个速度较快且精度较高的计算方法对于实现实时星光导航尤为重要。因此,图7 左图对比了不同折射计算模型的运算时间随计算天顶角个数的变化情况。可以看到,随着计算天顶角个数的不断增加,运算时间不断增加,其中多层大气折射计算模型运算时间较其他模型较长,这可能是由于多层大气折射模型的多次迭代计算造成的。对比等折射率法,可以发现等曲率法运算时间更长,这说明使用4 阶Runge-Kutta 的计算程序仍有待优化,后续可考虑使用Pytorch 库[50]在GPU 上进行运算来提升求解方程组的计算速度。与多层大气折射模型相比,基于SLALIB包计算速度相比其他解析模型最慢,这可能因为SLALIB 包计算需要从python 中不断调用Fortran 代码导致的[37]。图7 右图给出了不同解析折射计算模型在计算91 个天顶角后的运算时间对比,可以看到Cassini 模型和平面平行大气模型相比其他计算模型速度最快,而Mathar 气压指数模型相比其他模型速度最慢,Oriani三次方定理和五次方定理计算速度基本一致。因此,综合计算精度、计算速度和迭代次数,本文选取等折射率光线追迹法和Cassini 模型作为折射计算的模型。
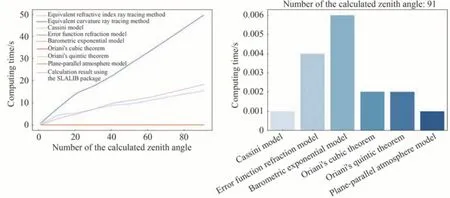
图7 不同折射计算模型的运算时间随天顶角个数的变化和91 个天顶角情况下不同理论折射计算模型的时间直方图Fig.7 The variation curves of the calculation time of different refraction calculation models as a function of the number of zenith angles and the time histograms of different theoretical refraction calculation models in the regime of calculating 91 zenith angles
2 我国典型区域折射计算结果
前一节我们介绍了不同的折射率模型以及折射计算模型,并分析和对比了不同折射计算模型的精度和速度,本节使用上一节选取的折射率模型以及折射计算模型来计算我国典型地区不同时刻、不同观测高度、不同观测天顶角以及不同波长下大气折射引起的折射角、色散角、横向位移、路径延长因子以及路径延时等物理量,为了解我国典型地区不同时刻的大气折射规律,实现星敏感器的准确观测、星光导航定位的精确校正提供数据支持。图8 是我国西北地区(以大柴旦为典型代表,90°10′ E~96°22′ E, 37°35′ E~39°12′ E,海拔2 829~5 655 m)和东南沿海(以台州为典型代表,124°34′ E, 28°50′ N,海拔162 m)某一天早晨和夜晚的实时观测数据绘制的大气温度、压强以及湿度随着高度的变化曲线,可以看到西北地区和东南沿海大气温度随高度整体呈现先降低后升高,且温度转折点通常位于对流层顶。另一方面,还可以发现早晨温度廓线明显小于夜晚温度廓线。除此之外,从图8 可以看到两地大气压强随高度整体呈现单调指数递减趋势,且早晚大气压强无明显差别,但相比于西北地区,东南沿海大气压强要高于西北地区。最后,从图8 最右侧一列,可以看出东南沿海大气湿度随高度整体呈现不断变小趋势,然而大柴旦早晚的湿度廓线并无明显规律,这可能是由于当日实测过程中天气变化所致,导致大气湿度在对流层出现反常增大。图9 是根据Ciddor 模型计算得到的折射率和折射率梯度的廓线,相比于美国标准大气,实测数据计算得到的梯度曲线抖动更加剧烈,为此我们对两地折射率梯度廓线进行分段平均处理。

图8 西北地区、东南沿海某天早晨和夜晚的大气温度廓线、压强廓线、相对湿度廓线Fig.8 Atmospheric temperature profile, pressure profile and relative humidity profile in the morning and night of a day of the northwest area and southeast coast of China

图9 根据Ciddor 模型计算的西北地区、东南沿海某天早晨和夜晚的折射率廓线,折射率梯度廓线Fig.9 Refractive index profiles, refractive index gradient profiles calculated from the Ciddor model in the morning and night of a day of the northwest area and southeast coast of China
2.1 折射角
2.1.1 不同观测高度
图10 是使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同观测高度情况下(即0 km,1.5 km,3 km,4.5 km,6 km ,7.5 km,9 km 和10 km,这里指的是相对于海平面以上的观测高度)折射角随天顶角的变化情况,本节计算在λ=0.9 μm 的基础上进行的。可以看到不同模型、不同地区和不同时间段折射角整体随天顶角的增加而不断变大,且Cassini 模型和等折射率光线追迹法的计算结果基本一致,仅仅在西北地区7.5 km~9 km 处出现几个微角秒的偏差,这可能是由于计算误差造成的。对比不同地区折射角的计算结果,可以看出东南沿海折射角明显大于西北地区,但整体变化趋势基本一致。进一步,对比两地不同时刻的折射角差异,还可以看到随着天顶角的增大,早晨和夜晚折射角出现明显的差异,这种差异的变化范围大约在5~10 个微角秒的数量级上变化。最后,我们还可看出西北地区早晚折射角差异要略大于东南沿海,但这种差异随着观测高度的增大逐渐消失,随着观测高度的增加,早晚折射角以及折射角差异随天顶角的变化也将逐渐减小,这是因为随着观测高度,光线因大气折射所走过的路径长度和弯曲程度不断变小,从而导致折射角逐渐减小导致的。

图10 使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同观测高度情况下折射角随天顶角的变化曲线Fig.10 The variation curve of refraction angle as a function of zenith angle for different observation altitudes in the morning and night of a day of the northwest area and southeast coast of China using the Cassini model and the equivalent refractive index ray tracing method
2.1.2 不同波长
图11 是使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同波长情况下(即0.9 μm,1 μm,1.1 μm,1.2 μm,1.3 μm,1.4 μm,1.5 μm 和1.65 μm)折射角随天顶角的变化情况,本节计算的观测高度为3 km。可以看到不同波长情况下使用Cassini 模型和等折射率光线追迹法计算的折射角基本无偏差。除此之外,还可以看到相比于西北地区,东南沿海的折射角要略大,不同波长下早晚折射角差异随天顶角的增大不断增大,且西北地区早晚折射角之差略大于东南沿海,这与上小节的规律基本一致。对比不同观测波长折射角随天顶角的变化曲线,可以看出折射角随观测波长在角秒量级无明显变化,需进一步调整变化单位进行比较。图12 是使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的折射角偏差随天顶角的在微角秒量级上变化情况(其中λ1=1 μm,1.1 μm,1.2 μm,1.3 μm,1.4 μm,1.5 μm 和1.65 μm,λ2=0.9 μm),可以看到不同波长下两波长折射角偏差随天顶角的增加不断增大,且相比西北地区而言,东南沿海在不同波长下的折射角偏差较西北地区偏大。除此之外,从图12 中可以明显的看到随着波长的增大,不同波长计算得到折射角差异也逐渐变大,但这种变化是在微角秒量级,这可能是因为波长对折射角的影响是通过折射率间接影响而导致的。

图11 使用Cassini模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同波长下折射角随天顶角的变化曲线Fig.11 The variation curve of refraction angle as a function of zenith angle for different values of wavelength in the morning and night of a day of the northwest area and southeast coast of China using the Cassini model and the equivalent refractive index ray tracing method
2.2 输入参数不确定性对折射角计算的影响
由前文的分析的可知,折射计算的准确性和精度不仅取决于折射率模型和折射计算模型的准确性,同样取决于输入数据的精度和准确度,然而在实际大气中进行探测测量时,所得的大气参数廓线将不可避免地受到随机噪声的影响,从而影响最终折射计算的准确度。为了定量分析大气参数廓线随机噪声误差对实际折射计算的影响,精确计算折射角计算误差和随机噪声之间的关系,本小节分别温度、压强、相对湿度、CO2浓度以及波长等角度计算了输入参数不确定对折射角计算的影响。图13~16 分别给出了使用Cassini模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同参数对应的不同输入参数误差情况下折射角误差随天顶角的变化情况。需要说明的是,本节计算假设温度、压强和相对湿度廓线所带来的误差满足高斯随机的正态分布,这也满足实际测量中大气参数廓线所附加的误差类型。
对比图13~16 中Cassini 模型和等折射率光线追迹法的计算结果,可以看出,使用Cassini 模型和使用等折射率光线追迹法计算得到输入参数不确定性对折射角的影响规律基本一致,只有在计算不同压强误差对折射角的影响表现出异常,可以看到使用Cassini 模型计算得到折射角误差明显高于等折射率光线追迹法,且误差是后者的好几倍。除此之外,对比图13 和图14 西北地区早晚折射角的误差数据,可以看出在较大的天顶角时,输入温度参数不确定性对早晨折射角计算影响偏大,输入相对湿度参数不确定性对夜晚折射角计算的影响偏大。另一方面,对比图15 和图16 东南沿海早晚折射角的误差数据,可以看出输入相对湿度参数不确定性对早晨折射角计算的影响偏大。总体而言,输入参数误差对西北地区折射计算的影响要明显小于东南沿海。最后,从图13~16 整体折射角误差的变化情况可以看到,随着观测天顶角和输入参数误差(包括温度、压强、相对湿度、CO2浓度以及波长)的增加,折射角计算所带来的误差也逐渐增加,这一点是不言而喻的。
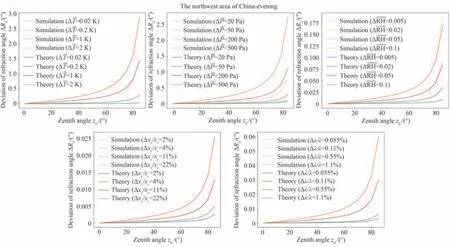
图14 使用Cassini 模型和等折射率光线追迹法计算的西北地区夜晚不同参数对应的不同输入参数误差情况下折射角误差随天顶角的变化曲线Fig.14 The variation curve of refraction angle error as a function of zenith angle under different input parameter errors corresponding to different parameters in the evening of the northwest area of China calculated using the Cassini model and the equivalent refractive index ray tracing method

图15 使用Cassini 模型和等折射率光线追迹法计算的东南沿海早晨不同参数对应的不同输入参数误差情况下折射角误差随天顶角的变化曲线Fig.15 The variation curve of refraction angle error as a function of zenith angle under different input parameter errors corresponding to different parameters in the morning of the southwest coast of China calculated using the Cassini model and the equivalent refractive index ray tracing method

图16 使用Cassini 模型和等折射率光线追迹法计算的东南沿海夜晚不同参数对应的不同输入参数误差情况下折射角误差随天顶角的变化曲线Fig.16 The variation curve of refraction angle error as a function of zenith angle under different input parameter errors corresponding to different parameters in the evening of the southwest coast of China calculated using the Cassini model and the equivalent refractive index ray tracing method
2.3 色散
图17 是使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同观测高度情况下(即0 km,1.5 km,3 km,4.5 km,6 km,7.5 km,9 km 和10 km,这里指的是相对于海平面以上的观测高度)色散角随天顶角的变化情况。需要说明的是,本节计算的0.9 μm 和1.65 μm 之间的色散现象。从图中可以看出东南沿海不同观测高度层早晚的色散情况要明显大于西北地区,另一方面,随着观测高度的增加,两地不同时刻的色散现象明显减弱,这与上一小节折射角的变化规律是一致的。除此之外,从图中还可以看出,不同高度层西北地区的早晚色散角差异要大于东南沿海,且随着观测高度的增加,这种趋势逐渐丧失。最后,与不同地区早晚折射角差异随观测高度变化规律一致的是,观测高度越低,两地早晚色散差异越大,这可能是由于色散差异随着传输路径增大不断累积导致的。


图17 使用Cassini 模型和等折射率光线追迹法计算的西北地区、东南沿海早晨和夜晚不同观测高度情况下色散角随天顶角的变化曲线Fig.17 The variation curve of dispersion angle as a function of zenith angle for different observation altitudes in the morning and night of a day of the northwest area and southeast coast of China using the Cassini model and the equivalent refractive index ray tracing method
2.4 横向位移
2.4.1 不同观测高度
第2 节介绍了星光经大气折射后产生横向位移的概念,表明了确定横向位移的大小有利于更精确的使用星敏感器定位大气层内的目标位置。本文将基于我国典型地区的一次探空数据,计算不同观测高度情况下星光折射横向位移的大小。图18 给出了西北地区和东南沿海早晨和晚上不同观测高度下横向位移b(∞)(h0)随天顶角的变化情况。在给出计算结果之前,需要说明的是,由式(7)、(8)和(10)可以看出,使用微分方程组求解横向位移时,需要折射率和折射率梯度曲线随高度变化的函数关系。为此,尽管横向位移的计算只使用西北地区和东南沿海30 km 以下的实测数据作为折射影响的主要因素,如图9 所示,但在使用四阶Runge-Kutta 法计算横向位移时通常需要高度超过30km 的数据作为生成n(h)和dn(h)/dh函数的来源。因此,在本节计算过程中,当h<30 km 时,我们使用实测气象探空数据根据Ciddor 模型计算得到的折射率和分段平均后折射率梯度曲线的线性插值函数作为生成n(h)和dn(h)/dh函数的来源(不同平均方法影响计算精度,经计算分段平均计算得到的折射角较滑动平均更接近直接积分法得到的结果);当h>30 km 时,由于折射率和折射率梯度随高度变化通常满足指数衰减规律,因此本文采用h<30 km 时折射率和分段平均后的折射率梯度曲线的指数拟合函数作为生成n(h)和dn(h)/dh函数的来源(在美国标准大气的验证计算中,我们使用了1 000 km 以下数据作为生成梯度函数的来源,这时计算的折射角更为接近标准值,这也是使用微分方程组进行折射计算的弊端,它通常需要更多的实测数据才能获得更高的精度)。除此之外,由图9(d)可以看出,东南沿海夜晚的折射率梯度曲线在2 km 高度以下存在数值跃变,因此在对东南沿海夜晚折射率梯度数据进行拟合时,采用了2 km 以上的数据进行指数拟合,此时计算得到折射角与Cassini 模型给出的结果基本接近,验证该方法的可行性。

图18 西北地区和东南沿海早晨和晚上不同观测高度下横向位移随天顶角的变化曲线Fig.18 The variation curves of lateral shift as a function of zenith angle under different observation heights in the morning and evening of the northwest area and southeast coast of China
从图18 中可以看出西北地区和东南沿海早晚不同观测高度下的横向位移整体与天顶角呈现正相关关系,且随着天顶角的增大,横向位移增加的速率也不断变大,尤其当天顶角为85°时,横向位移呈现量级上的增长。与此同时,通过对比西北和东南沿海两地横向位移的大小,可以发现西北地区折射引起横向位移的大小较东南沿海地区偏大。另一方面,对比不同高度层(即0 km,1.5 km,3 km,4.5 km,6 km,7.5 km,9 km、10 km 和15 km,这里指的是相对于海平面以上的观测高度)的观测结果,可以发现两地观测的横向位移的大小随着观测高度的增加不断减小,这也是合乎情理的,因为观测高度越高,星光因折射而产生的弯曲效应也越小。值得注意的是,当天顶角较小时,观测高度从0 km~15 km 变化时横向位移基本减小了一个数量级。除此之外,对比两地不同高度下早晚横向位移随天顶角的变化规律可以看出,夜晚相比早晨折射产生的横向位移偏大,随着观测高度的增大,早晚两时横向位移产生的偏差逐渐减小,且当天顶角较小时,早晨的横向位移会逐渐大于夜晚的结果。
2.4.2 不同波长
图19 是西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的横向位移偏差随天顶角的在微米量级上变化情况(其中λ1=1 μm,1.1 μm,1.2 μm,1.3 μm,1.4 μm,1.5 μm 和1.65 μm,λ2=0.9 μm,且本节计算在观测高度为3 km 的基础上进行的),可以看到不同波长下西北、东南两地早晨和夜晚的两波长横向位移偏差整体随天顶角的增加而不断变大。除此之外,对比两地早晨和夜晚的两波长位移偏差数据可以看出当天顶角较大时,夜晚较早晨而言两波长横向位移的偏差更大。另一方面,对比西北地区和东南沿海的结果,可以看到西北地区波长引起的横向位移偏差要大于东南沿海,说明西北地区波长对横向位移的影响更大。最后,通过对比不同波长下两波长产生的横向位移偏差,可以看到随着波长的增大,不同波长计算得到横向位移差异也逐渐变大,且当天顶角较小时,这种差异较为明显。值得注意的是,这种变化是在厘米量级进行的,这可能也是由于波长对折射角的影响是通过折射率间接影响导致的。
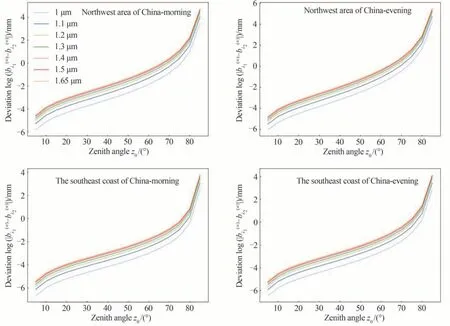
图19 西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的横向位移偏差随天顶角的变化曲线Fig.19 The deviation of lateral shift calculated at two wavelengths as a function of zenith angle under different values of wavelength in the morning and night of the northwest area and southeast coast of China
2.5 路径延长因子和路径延时
2.5.1 不同观测高度
大气折射使得光线经过大气传输产生弯曲现象,延长了光线传输的路径,增加了光束信号的延时,是星光导航定位技术的主要误差来源之一,为此,本小节针对我国典型地区不同时段,不同观测高度计算了大气折射引起的路径延长因子以及路径延时,并针对不同区域、时间和高度下路径延长因子给出了拟合得到的多项式函数。图20 给出了西北地区、东南沿海早晚不同观测高度层下路径延长因子和路径延时随天顶角的变化情况,通过计算得到的数据,给出了两地不同高度层下早晚路径延长因子随天顶角变化的多项式拟合函数(以西北地区早晨和东南沿海地区夜晚观测高度为3 km 时的数据为例)。

图20 西北地区、东南沿海早晚不同观测高度层下路径延长因子和路径延时随天顶角的变化曲线Fig.20 The variation curves of path elongation ratio and path delay as a function of zenith angle under different observation heights in the morning and evening of the northwest area and southeast coast of China
西北地区早晨3 km时的拟合函数为
东南沿海夜晚3 km时的拟合函数为
由图20 可以看出路径延长因子和路径延时随天顶角的增大不断增大,当天顶角较大时,这种增大最为剧烈。除此之外,路径延时基本在微秒量级上变化,且西北地区和东南沿海不同高度下早晨和夜晚和路径延长因子和路径延时基本完全重合,通过早晚路径延长因子和延时偏差随天顶角的变化曲线可以看出,随着天顶角的增加,延长因子和延时的偏差整体不断增加。另一方面,可以看到延长因子的变化主要在10−8数量级以下范围内变化,而延时主要在纳秒量级左右上下波动,并且这种变化随着观测高度的增加量级上将变得更小,因此,可以指出不同高度下两地早晚的延长因子和延时的差异可以几乎忽略不计。对比西北地区和东南沿海的计算结果,可以看出东南沿海大气折射造成的路径延长比和路径延时相比与西北地区较大。最后,还可以看出随着观测高度的降低,不同天顶角下延长因子和延时整体逐渐减小,这与之前折射角和横向位移得到的结论是一致的。
2.5.2 不同波长
图21、22 是西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的路径延长因子偏差和延时偏差随天顶角的变化情况(其中λ1=1 μm,1.1 μm,1.2 μm,1.3 μm,1.4 μm,1.5 μm 和1.65 μm,λ2=0.9 μm,且本节计算在观测高度为3 km 的基础上进行的),可以看到不同波长下西北、东南两地早晨和夜晚的两波长延长因子和延时的偏差整体随天顶角的增加而不断变大,且不同波长下两波长延长因子偏差主要在10−10以下范围进行波动,延时偏差主要在纳秒量级上左右波动,因此可以认为波长对路径延长因子和路径延时的影响可以忽略不计。除此之外,还可看出两地早晨和夜晚的两波长延长因子和延时的偏差基本一致,这说明不同时段波长对延长因子和延时的影响并不差别。最后,从图20 还可以看出东南沿海地区两波长路径延长因子偏差较西北地区偏大,这说明东南沿海波长对延长因子的影响更大,但由于波长对延长因子和延时的影响几乎可以忽略不计,因此这种影响并不重要。
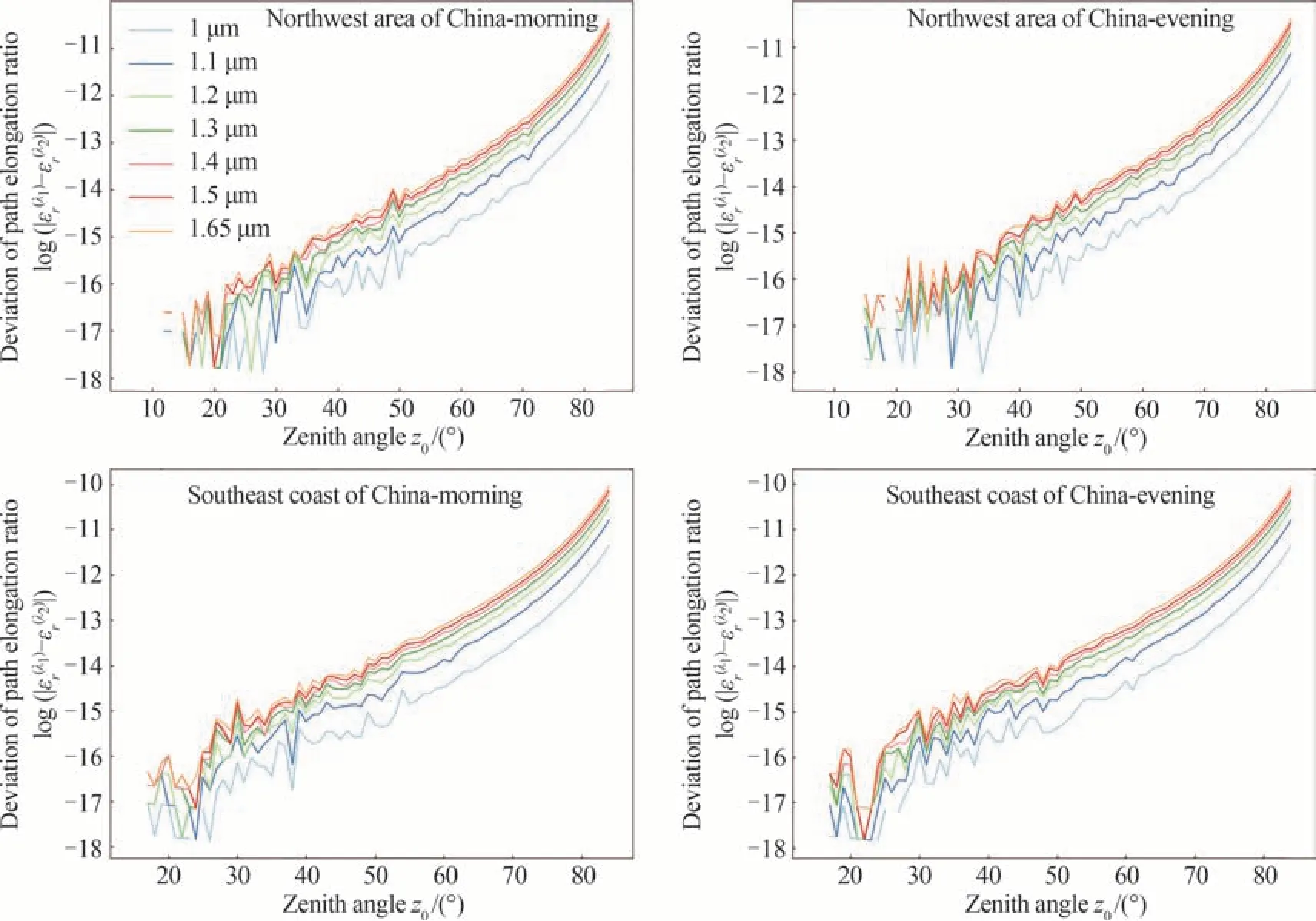
图21 西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的路径延长因子偏差随天顶角的变化曲线Fig.21 The deviation of the path elongation ratio calculated at two wavelengths as a function of zenith angle under different values of wavelength in the morning and night of the northwest area and southeast coast of China
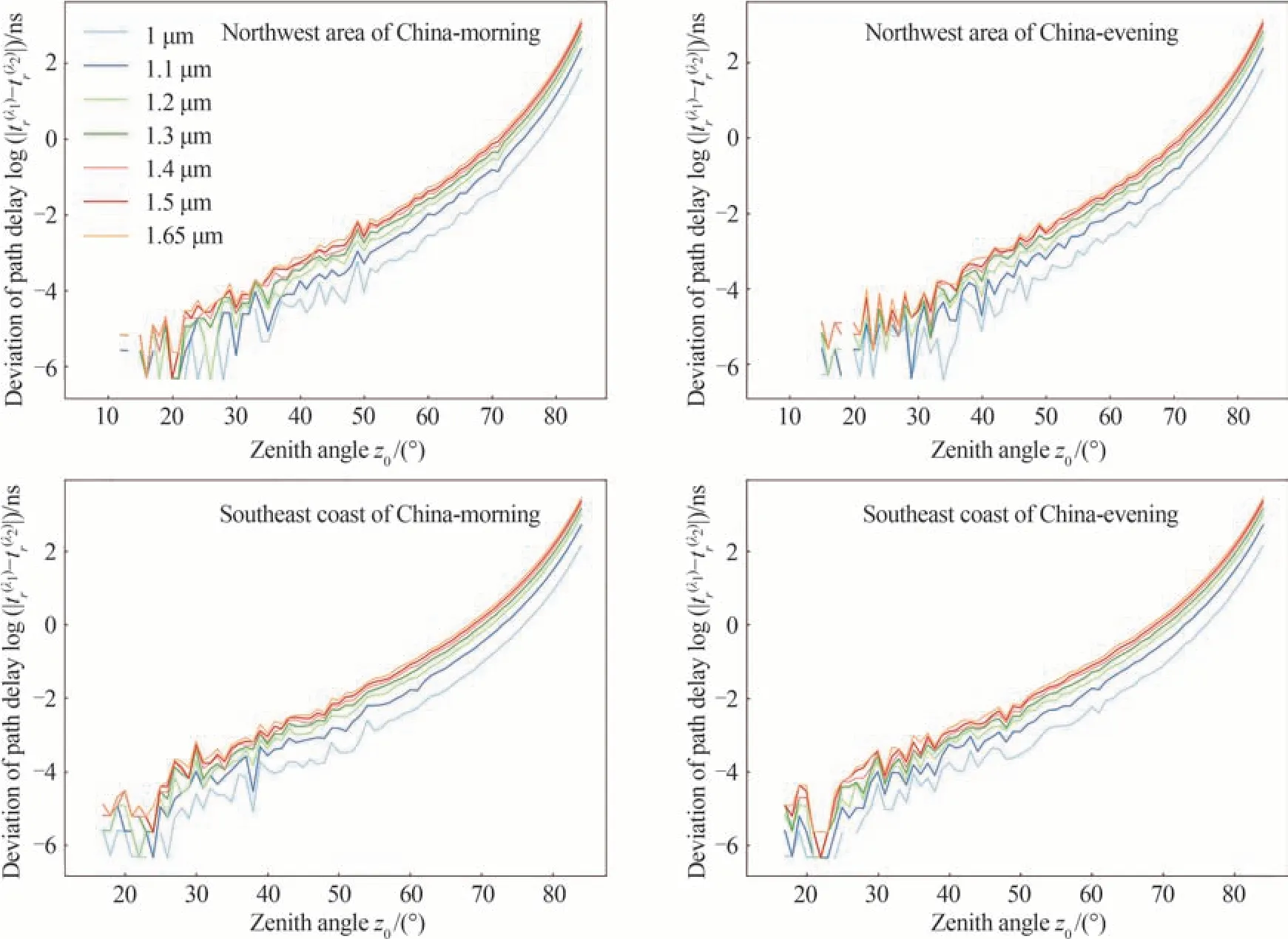
图22 西北地区、东南沿海早晨和夜晚不同观测波长下两波长计算的路径延时偏差随天顶角的变化曲线Fig.22 The deviation of the path delay calculated at two wavelengths as a function of zenith angle under different values of wavelength in the morning and night of the northwest area and southeast coast of China
3 结论
本文选取最佳的星光大气折射模型,着重研究了大气折射对星光成像的影响。根据美国标准大气给出的大气参数廓线数据,计算了平面平行大气、整层球形大气以及多层球形大气模型下的折射角的变化特性,对比分析了不同折射计算模型的计算精度和计算速度,选取了精度和速度最佳的折射计算模型。与此同时,针对多层球形大气折射模型,研究了计算结果与迭代次数(即大气层数)之间的关系,计算了美国标准大气情形下大气折射产生的横向位移、路径延长因子和路径延时,验证了多层球形大气折射模型的可靠性和普适性。结合典型地区不同时段实测的大气参数廓线数据,计算了不同观测条件以及不同波长情况下的折射角、色散、横向位移、路径延长因子以及路径延时的变化情况,评估了不同大气参数由于输入参数的不确定性对折射计算的影响。研究发现:1)使用Ciddor 折射率模型并结合Cassini 折射计算模型或等折射光线追迹法计算得到的折射角最为准确;2)相比于改变观测波长而言,提升星敏感器的观测高度或减小星敏感器的观测天顶角能极大程度上减轻星光成像的大气折射影响;3)当不同输入参数存在噪声和不确定性时,温度参数不确定性对折射计算的影响最大。因此,为了能一定程度上减轻折射计算的误差,有效提高温度的测量精度相比修正其他参数的不确定性而言更为重要。
附录
A.1 Corbard 误差函数模型
Corbard 误差函数模型假设大气密度随高度呈现指数衰减,表示为
式中,δn0=n0−1,t=hr/r⊕,为式(3)或(4)给出的大气折算高度与地球半径(为海平面观测点对应的地球的曲率半径)的比值,
A.2 Oriani 定理
Oriani 定理也称为Oriani 三次方定理
式中,A和B分别代表常数。若对等式(A1)中的Ψ(x)采用Laurent 级数进行展开,可得到关于大气折射角计算的另一个等式,即Oriani 五次方定理
A.3 Mathar 气压指数模型
Mathar 气压指数模型通过折射率(磁化率)随高度呈指数衰减的大气模拟望远镜位置上方的折射率,它通常指的是将折射角的直接积分公式Taylor 展开成奇数阶的tanz0的函数
式中,σi(i=1,3,5,…)可根据磁化率随高度呈指数衰减的假设计算得到
式中,μ0=n20−1,代表磁化率。

