基于高精度卫星激光测距数据的漂移误差分析与研究
李知非,汤儒峰,翟东升,3,4,李祝莲,3,4,伏红林,4,黄凯,曹进,,李语强,3,4
(1 中国科学院云南天文台,昆明 650216)
(2 中国科学院大学,北京 100049)
(3 中国科学院空间目标与碎片观测重点实验室,南京 210023)
(4 云南省太阳物理与空间目标监测重点实验室,昆明 650216)
(5 乐山师范学院 数理学院,乐山 614000)
0 引言
卫星激光测距(Satellite Laser Ranging, SLR)是通过精确测定激光脉冲从地面观测站发送到卫星的往返时间间隔来测量观测站与卫星距离的技术,其测距精度可达厘米级。SLR 主要应用于精密确定卫星轨道、精确测量地球自转参数、精密建立地球参考系等[1]。这些科学应用也推动着SLR 技术向获得高质量、高精度的数据发展。
目前,国内外大多数激光测距站采用的探测器是单光子雪崩二极管(Single Photon Avalanche Diode,SPAD)[2-5]。SPAD 量子效率高,时间响应快速,且灵敏度高,可以探测到最少为单光子量级的激光脉冲回波[1],这对于回波微弱但又需要获得高精度数据的SLR 来说十分合适,所以在SLR 系统中得到了广泛的应用。但由于SPAD 的探测特性,其在工作时会在测距结果中引入漂移误差(Walk Error)[6],该误差会对激光测距的精度产生影响。针对漂移误差,国内外科研人员已经做了诸多研究。2010年,OH M S 等对基于SPAD 的激光雷达做了探测概率模型描述,并对基于SPAD 的激光雷达测量结果中的漂移误差进行分析与改正[7]。2013年,徐璐等针对基于SPAD 的激光雷达系统提出了一种新的回波信号处理方法来抑制漂移误差[8]。2015年,OTSUBO T 等对于激光测距不同回波光子数对质心修正的影响做了统计,其中也包含了对漂移误差抑制方法的讨论[9]。2018年,黄科等利用SPAD 的探测概率模型计算漂移误差,并对激光测距结果进行了修正[10]。
目前国内外的研究主要针对基于SPAD 探测器的激光雷达,从探测器的探测模型出发对漂移误差进行分析与研究,但对于卫星激光测距领域的漂移误差分析较少,对于实际测距数据在漂移误差分析与研究中的应用也较少,且目前结合实测数据对漂移误差的研究较少,缺乏针对性。在卫星激光测距精度向毫米级甚至亚毫米级进军的今天,这个问题需要被考虑和讨论。对于实际测距数据进行针对性分析,可以更准确地减小测距数据中的漂移误差,从而进一步提高测距数据的质量。本文将对卫星激光实际测距数据的分析加入到漂移误差的补偿过程中,通过实际测距数据与仿真模型相结合,有效减小卫星激光测距数据中的漂移误差,从而提高数据质量,提高测距精度。
1 理论分析
1.1 漂移误差产生的原因
在卫星激光测距测量处在某一特定位置的目标时,由于人为因素或者环境因素,回波能量会产生波动,测量数据所对应的距离值分布也会随之波动,这些波动会导致测量距离出现误差,即漂移误差。漂移误差产生的根本原因在于回波能量的波动,所以首先推导出由实际测距数据计算回波能量,即回波光子数的方法。
1.1.1 平均回波光子数的计算方法
卫星激光测距数据接收端常用的探测器SPAD 无法直接测量到平均回波光子数,但是其探测概率计算公式中包含平均回波光子数,所以可以通过统计实际测距数据结果得到探测概率,再由探测概率反推平均回波光子数,进一步可以计算得到漂移误差。对于SPAD 探测器来说,当平均回波光子数为n0时,探测器探测到n个光电子的概率为[11]
由于对SPAD 来说,当光电子的数量不为0 时即为被触发状态,所以探测器被触发的概率即为n≥1 的概率,而探测器不被触发的概率即为n=0 的概率。设信号到来前噪声回波光子数量为nn1,那么探测器被噪声触发的概率Pfa(噪声触发概率)为
设在回波持续时间内,信号回波光子数量为ns,噪声回波光子数量为nn2(ns远大于nn2),那么探测器在该段时间被触发的概率Ps(信号触发概率)为
因为在一个距离门时间内,SPAD 只能被触发一次,故信号探测概率Pe应为
所以,对实测数据进行统计,得到信号到来前的噪声触发概率为Pfa,信号探测概率为Pe时,可反推信号回波光子数ns为
同理,噪声回波光子数nn1为
因为噪声进入到探测器在时间上为均匀分布,所以,若第一段时间长度为Tn,第二段时间长度为Ts,则第二段时间的噪声回波光子数nn2为
由以上分析可知,对卫星激光测距结果进行统计,就可以反推出平均回波光子数,进一步可以通过仿真计算对应的漂移误差,修正误差项,进而提高卫星激光测距的数据质量和精度。
1.1.2 仿真不同回波光子数的探测概率分布情况
将式(1)进一步写为[12]
式中,P(m;ti,tk)表示在ti到tk这段时间内探测器触发了m个光电子的概率,m表示在这段时间内触发光电子的数量,M(ti,tk)表示在ti到tk这段时间内进入到探测器内的光子数量。那么在一个距离门的时间内,如果探测器在第j个时隙被触发,那就要求在前j−1个时隙内不被触发。故探测器在第j个时隙被触发的概率为
这样可以计算出在一个距离门事件内,探测器在每个时隙的触发概率,从而得到探测概率曲线;改变平均回波光子数量,就可以得到不同平均回波光子数对应的探测概率曲线。由1.1.1节的计算方法可得,卫星激光测距的平均回波光子数为0~10个,则仿真得到该范围内不同平均回波光子数的探测概率分布情况如图1所示。
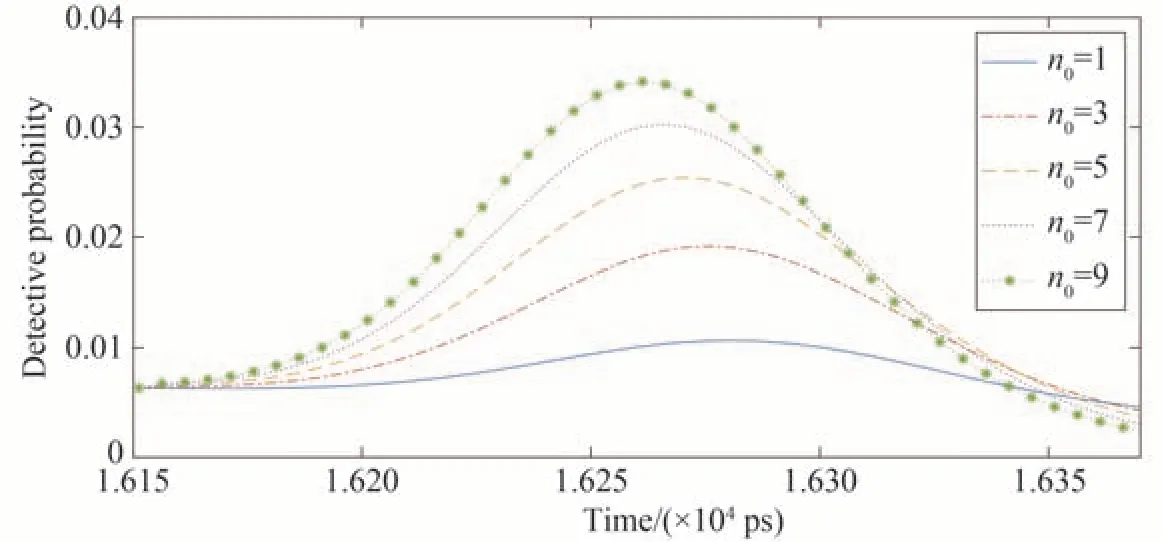
图1 不同回波光子数对应的探测概率分布Fig.1 Detection probability distribution of different echo photon numbers
由图1 可知,当回波光子数增加时,探测概率的峰值前移,意味着测量数据分布中,更近的位置将会有更多的探测点,导致卫星激光测距的解算距离更近。
1.2 漂移误差的仿真计算方法
当对接收到的信号进行分析、解算距离时,所依赖的正是基于探测概率所得到的探测情况。由探测概率解算激光飞行距离Rc的计算公式为
式中,0~T为信号回波持续的时间段长度,p(t)为该时间段内信号的探测概率,r(t)为该时间段内每一个探测概率所对应的距离值。用此式(10)计算出加权平均值作为探测概率解算距离值。设目标实际距离值为R,则漂移误差Rw的计算公式为
因卫星激光测距的平均回波光子数为单光子量级,故对0.1~10 个回波光子进行仿真计算,解算得到的激光飞行距离如图2 所示,漂移误差如图3 所示。
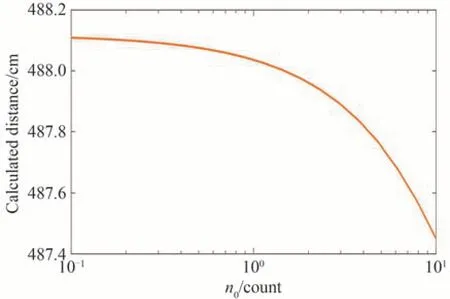
图2 解算得到的激光飞行距离与平均回波光子数的关系Fig.2 Relationship between calculated distance and average echo photon number
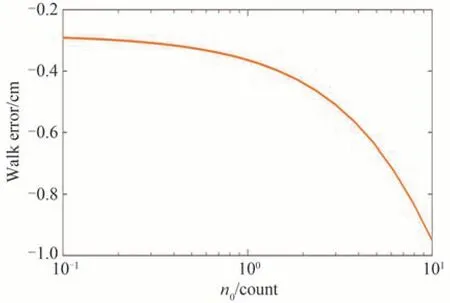
图3 漂移误差与平均回波光子数的关系Fig.3 Relationship between walk error and average echo photon number
1.3 常规测距系统中系统时延标校过程中的漂移误差分析
卫星激光测距过程通常会采用地靶测量的方法标校系统延时[13]。在进行地靶测量时,往往会人为衰减激光能量,这是为了将地靶回波信号能量大小尽可能与卫星回波信号能量大小相匹配,从而减少两者的漂移误差差值。但由于对激光能量无法做到精细控制,所以漂移误差在激光测距中仍然存在。由激光雷达方程估算测量LAGEOS 卫星和地靶时的回波光子数[14]为
式中,Nr为脉冲平均回波光子数,E0为每一束激光脉冲的能量,N为每焦耳能量激光包含的光子数,Te为发射系统光路的透过率,Am为目标的横截面积,ρ为目标的反射率,Ar为接收望远镜的有效接收面积,Tr为接收系统的光学效率,η为探测器的量子效率,Ta为单程大气透过率,Ω为激光反射发散角,θe为激光出射发散角,D为激光发射的光束的直径。按照表1 的参数,计算测量LAGEOS 卫星和地靶时的回波光子数,再将计算结果输入到探测概率公式(9)和漂移误差计算公式(11)中,计算漂移误差情况,结果如图4 所示。可知,由于两者的回波光子数不同,所以漂移误差有区别,在这种情况下,如果直接使用地靶测量结果去修正卫星测量结果,势必会引起误差,使测距数据质量下降。

表1 53 cm 双筒激光测距系统参数Table 1 53 cm binocular laser ranging system parameters
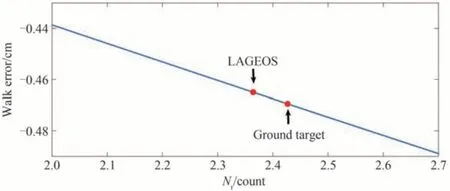
图4 LAGEOS 卫星和地靶的回波光子数差导致的漂移误差差值示意图Fig.4 The difference of walk error caused by the difference of echo photon number between LAGEOS satellite and ground target
2 卫星激光测距实测数据结合理论模型的漂移误差补偿方法
基于理论分析提出一种卫星激光测距中由实际测距数据结合理论模型的漂移误差补偿方法。
2.1 地靶测量数据处理
首先,对地靶测量数据进行信号识别[15],识别结果如图5 所示。再结合标称值计算地靶系统延迟;统计信号光子数与信号到来前的噪声光子数,结合测量时间计算噪声触发概率与信号探测概率,进而计算得到信号触发概率,由概率计算出地靶平均回波光子数以及测量地靶对应的漂移误差。设由地靶测量数据的识别结果计算得到系统延迟为Δ,进而得到的地靶漂移误差为Rwalk_error(ntb)。

图5 地靶信号识别结果Fig.5 Identified data of ground target
2.2 卫星测量数据处理
其次,对卫星测量数据进行处理。将计算得到的系统误差加入到卫星测距数据中,对卫星测距数据进行信号识别,识别结果如图6 所示。由识别结果计算卫星测量距离;统计信号光子数与信号到来前的噪声光子数,结合测量时间计算噪声触发概率与信号探测概率,进而计算得到信号触发概率,由概率计算出卫星平均回波光子数以及该测量时段对应的漂移误差。设由卫星测量数据计算所得的卫星测量距离为R,卫星漂移误差为Rwalk_error(nsat)。

图6 卫星信号识别结果Fig.6 Identified data of satellite
2.3 漂移误差补偿
最后,将计算得到的地靶漂移误差和卫星漂移误差加入卫星信号识别后解算的卫星测量距离结果中进行漂移误差补偿,得到修正后的距离结果。修正结果为
3 回波时变下卫星激光测距漂移误差的补偿
3.1 回波时变下卫星激光测距漂移误差补偿方法
在卫星激光测距的每一圈测距数据中,也存在着回波能量随时间波动的情况,所以对每一圈数据,将其中的信号划分为10 s 一段的片段进行光子数统计以及漂移误差的计算和补偿工作;在做该数据分析时,由于卫星和测站之间的距离是在时刻变化的,所以不能直接对计算出来的标准点数据(Normal Point, NP)进行计算判断,而是将标准点数据去势后进行计算。对于一圈数据所有划分的片段,计算其去势标准点数据修正前和修正后的均方根(Root Mean Square,RMS)来说明数据质量的提高。
3.2 方法应用实例
对2019年1月18日KOMPSAT-5 卫星的测距原始数据进行分段计算,并补偿测距数据中的漂移误差,得到结果如图7 所示。图7 中每一个数据点均为去趋势后的标准点数据,可以看到经过漂移误差补偿后,整个数据的RMS 降低,说明数据离散程度更低,数据波动更小。这表明数据中因漂移误差导致的距离值波动经过处理后变小,数据质量有所提高。

图7 减小漂移误差对卫星激光测距数据的影响Fig.7 SLR data with the influence of walk error reduction
3.3 批量数据处理结果分析
对2017年至2022年间持续观测的6 个目标卫星:Ajisai、Jason-3、KOMPSAT-5、LARES、Stella、Swarm-B 的部分激光测距数据进行补偿漂移误差处理,得到结果如图8。

图8 减小漂移误差前后的卫星激光测距数据对比结果(2017年—2022年)Fig.8 Comparison results of satellite laser ranging data before and after walk error reduction (2017—2022)
由图8 可以看出,经过补偿漂移误差后的数据,去势标准点的RMS 都有所降低,反映出数据中由于能量变化带来的波动被有效降低,数据质量有所提高。对于不同卫星来说,修正量最多的为Swarm-B 卫星,平均修正量为450.7 ps,这是由于Swarm-B 卫星轨道高度低(460 km),运行速度快,在进行常规卫星观测时,望远镜会为了跟上目标而快速移动,导致激光光束无法时刻对准卫星,使回波能量变化比较大,数据中的漂移误差也就比较大。而轨道较高的目标,例如Jason-3 卫星(轨道高度1 336 km),其运行速度较慢,过境时间长,望远镜比较容易锁定目标,回波信号能量大小比较稳定,数据中的漂移误差也就比较小,平均修正量为28.5 ps。所以,对于轨道高度较低的目标,漂移误差对数据的影响较大,如果能够对其测距数据中的漂移误差进行有效减小或降低,将会显著提升数据质量。
4 结论
本文利用中国科学院云南天文台53 cm 双筒激光测距系统的实际测距数据和仿真,对卫星激光测距数据中存在的漂移误差进行了分析与补偿。研究结果表明:在卫星激光测距中,能量波动会导致数据中存在漂移误差,这些漂移误差能够通过计算得出,将对该误差的补偿加入到数据处理过程后,测距数据质量会得到提升。本方法将卫星激光测距的实测数据加入到补偿过程中,与单纯考虑模型相比能够更有针对性、更准确且实时地对漂移误差进行抑制,也在一定程度上弥补了现有的对卫星激光测距数据处理方面的不足,能为卫星激光测距的数据处理过程提供参考。但本文通过仿真计算出的漂移误差没有经过实验验证,为理论上的计算值。后续工作中,可以通过实验计算数值,以更精确地确定漂移误差数值,更大程度地减小漂移误差对实际测距数据的影响。

