基于滑模控制器的四旋翼飞行器控制方法

王 磊,刘尧林,张 伟,贾梦梦,孟瑞锋

(1.陆装航空军代局驻景德镇地区航空军事代表室,江西 景德镇 333002;2.陆军装备部航空军事代表局,北京 100080;3.内蒙古工业大学,内蒙古 呼和浩特 010051)

0 引言

在飞行过程中,四旋翼飞行器各通道间耦合性很强,具有典型的非线性特性。未知的外界干扰和模型参数偏差等问题的存在,会影响控制器对四旋翼飞行器的控制精度。

针对上述问题,本文采用反步法的思路设计滑模控制器。首先从一个高阶系统的内核开始,保证内核系统的稳定性,设计虚拟控制律;然后对虚拟控制律进行修正,完成系统控制器的设计。因为滑动模态运动和系统的不确定性及系统所受的干扰不存在依赖性,具有较好的鲁棒性,所以采用滑模控制算法设计控制器,能对全系统控制调节,达到预期性能,工程中也易于实现,已经在很多领域中得到广泛应用。

1 系统模型的状态空间描述

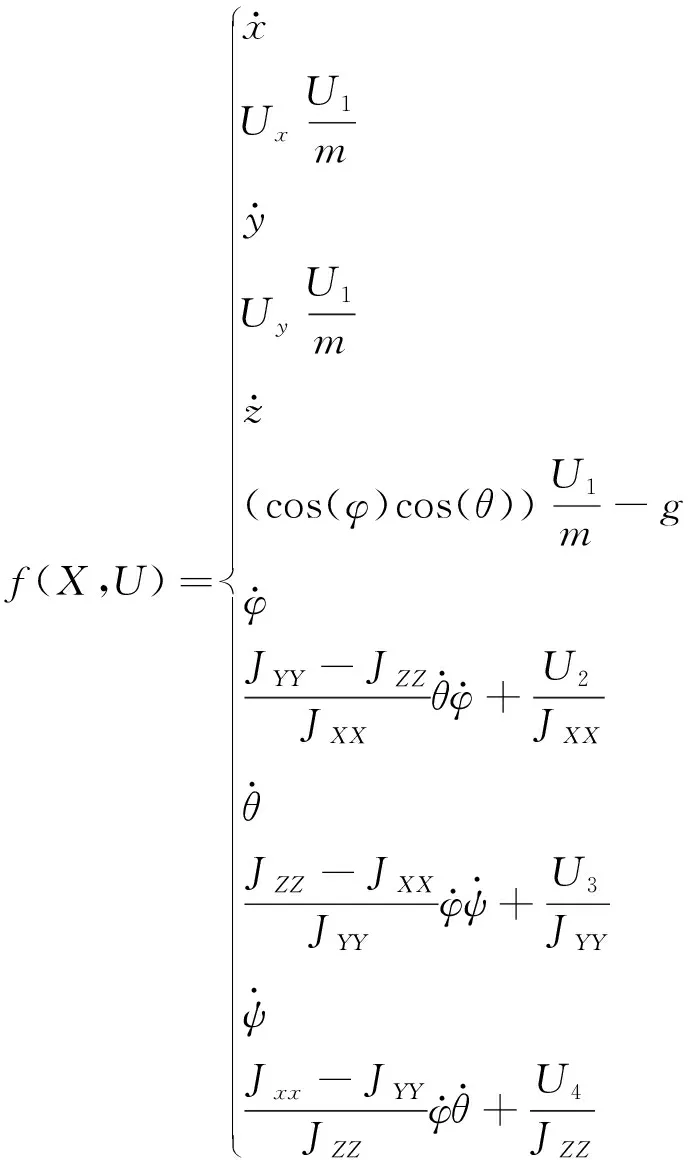
(1)

其中

利用高为炳教授提出的大系统思想,设置六个子系统解耦四旋翼飞行器系统。在建立完成的每个子系统中,已知其他变量,只研究一个输出量和一个输入量的变化[1]。从滑模控制框图1中可以看出,其他变量由其他的子系统调整后的值输入进来。

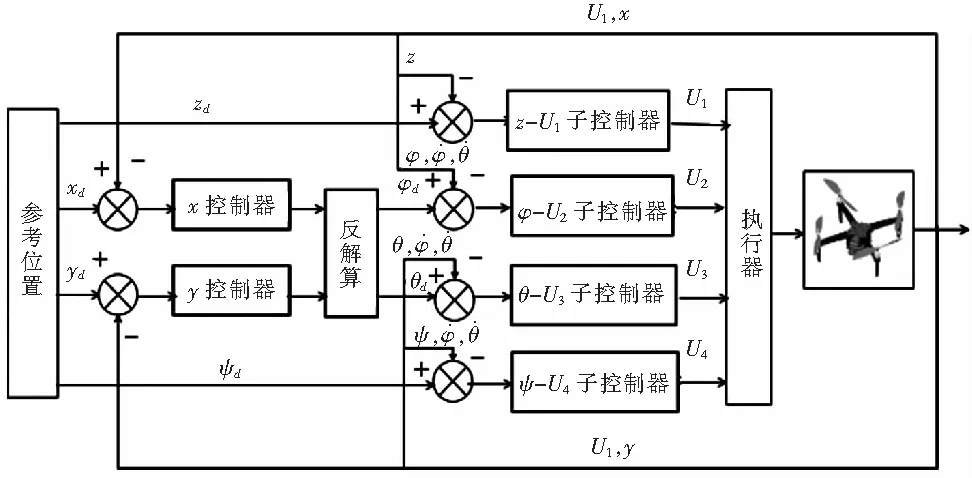
图1 四旋翼飞行器滑模控制框图

2 利用反步法设计滑模控制器

2.1 姿态角子系统控制器设计

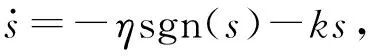
选择俯仰角θ和偏航角ψ的滑模面:

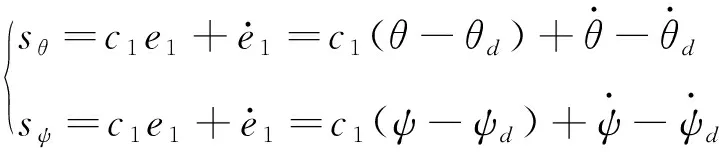
(2)

按照同样步骤,推导出U3和U4:

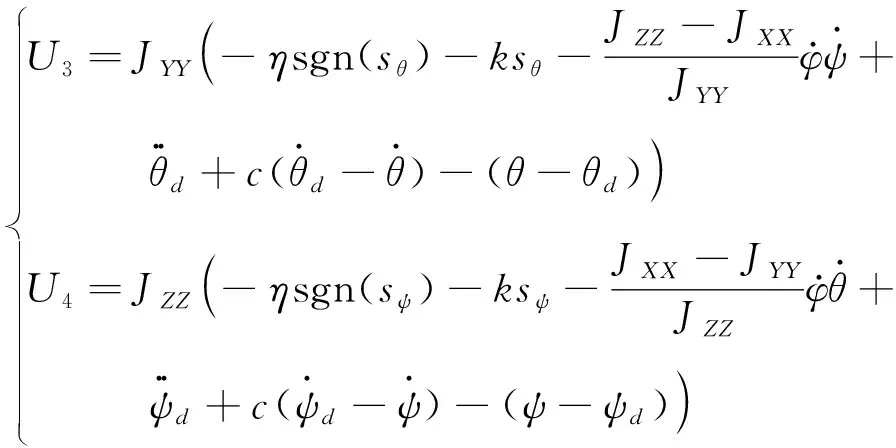
(3)

2.2 位置子系统控制器设计

1) 设计水平面x轴和y轴的滑模控制算法,根据以上子系统控制器设计的步骤选择滑模面:

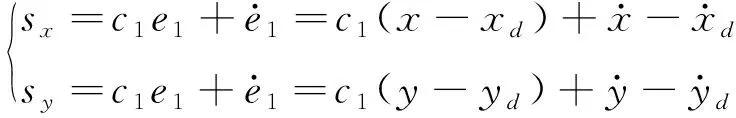
(4)

同理,推导出x轴和y轴的控制律Ux和Uy:

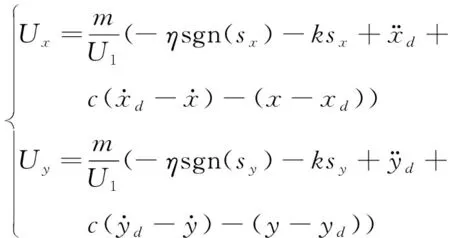
(5)

由状态空间方程,反解算出内环姿态控制的目标输入量θd和φd,得出下列方程:

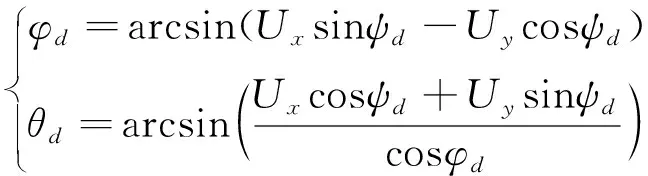
(6)

2)z-U1的控制器设计

系统各个子系统的控制律整理如下式:

(7)

2.3 未知扰动下的自适应滑模控制

提出自适应的方法去估计未知扰动,并根据估计出的未知扰动,设计相应的控制器。参考文献[4]-[8],控制器设计如下。

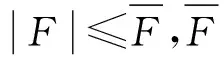
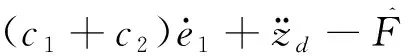
(8)

自适应律设计为:

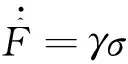
(9)

求得:

-eTQe-η|σ|≤0

(10)

其中,

(11)

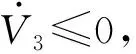
3 仿真试验

3.1 滑模控制器在无扰动下的仿真

当给定位置信息时,内环的输入目标值,通过外环的位置控制回路反结算,算出内环的输入量。

根据滑膜控制仿真框图(图2),选取目标值(x,y,z)为(1,1,2),偏航角为1,也就是飞行器从坐标系原点(0,0,0)到(1,1,2)的飞行过程中,进行滑模动态的控制效果验证。选取控制器的相关系数如表1。

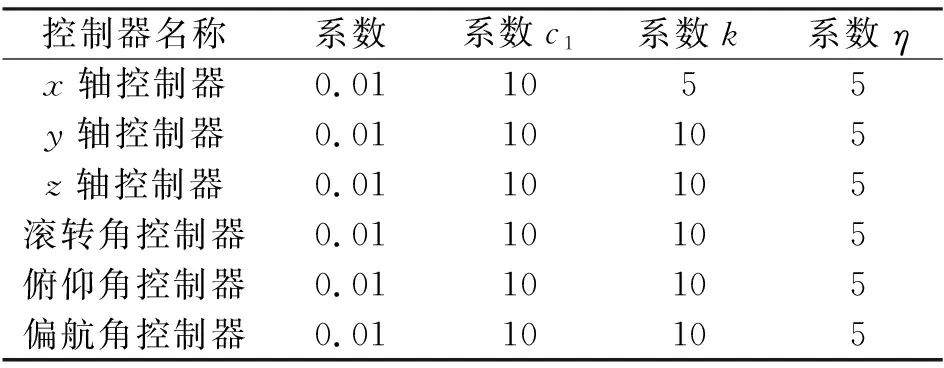
表1 滑模控制器相关参数

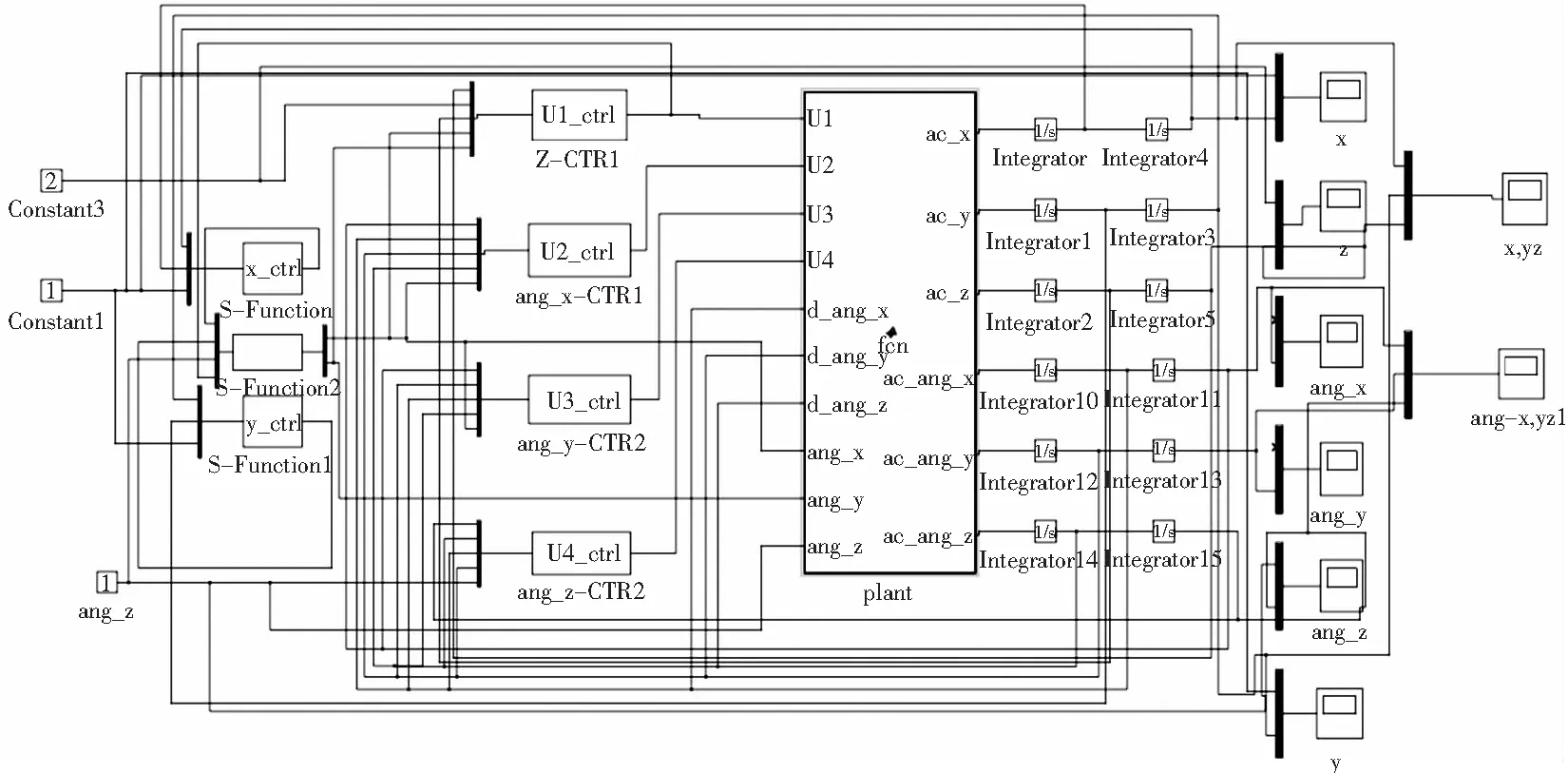
图2 滑模控制仿真框图

将表1的系数输入对应的控制器中,可以看到趋近速度系数k不同时,响应的速度也不同,造成传入内环输入量的快慢也不同,进而,内环的响应速度也不同,在图3和图4中,都可以看出。

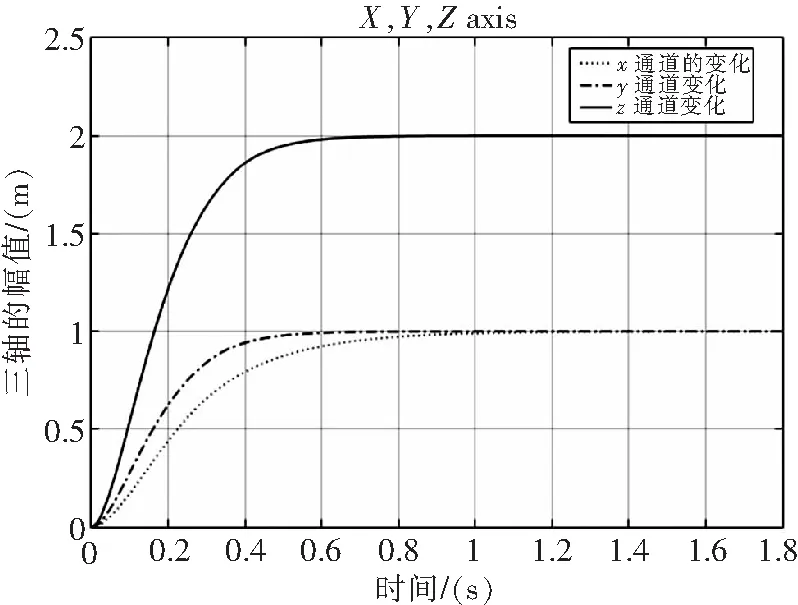
图3 位置响应曲线

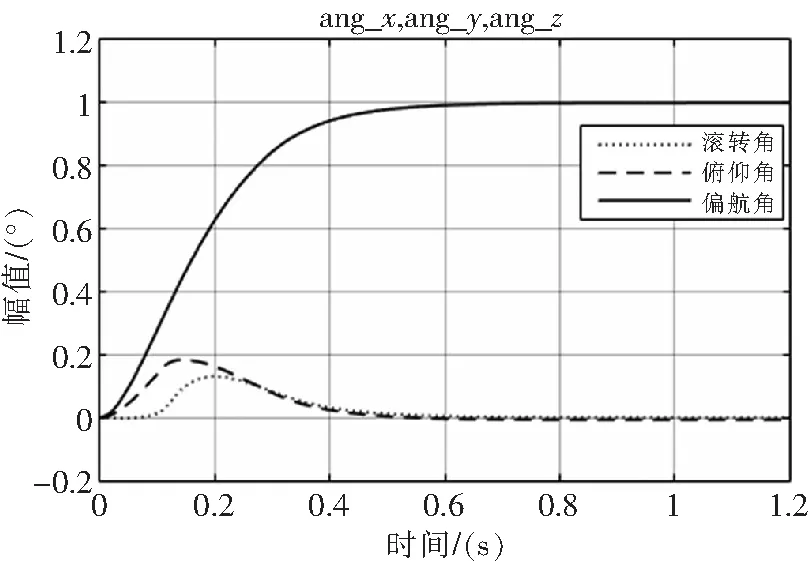
图4 姿态角响应曲线

通过图3和图4位置和姿态角响应曲线的分析,位置和姿态角都在0.8 s到达稳定。

3.2 滑模控制器在有界扰动下的仿真分析

滑模控制器对有界扰动有很好的鲁棒性,本节通过输入两种外部扰动信号给z轴通道的模型,验证其效果。输入扰动信号dt=5sint给飞行器z轴通道的模型,效果如图5;输入扰动信号dt=20sint给z轴通道的模型,效果如图6。

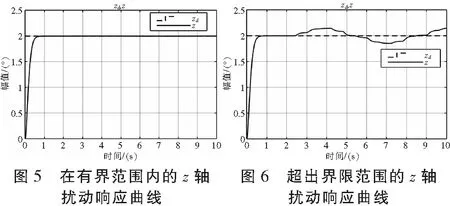
从图5分析可知,当扰动dt=5sint时,|dt|≤η,扰动设置为1.8 s后输入。可以看出,系统的稳定性较好,说明在原有的滑模控制器不变的情况下,对有界扰动具有很好的鲁棒性。由图6分析可知,当超出系统可承受的界限就出现巨大抖动,系统的稳定性变差。

3.3 未知扰动下的自适应滑模控制

系数δ=0.01,k=4,c1=2.5,γ=12,η=0.15,c2=2.5,代入满足矩阵Q正定,则F的估计值和F的输入值如图7-图8。

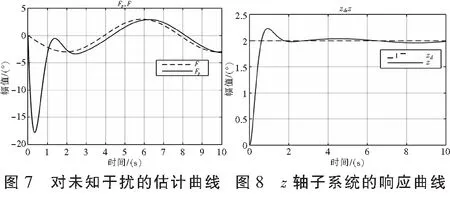
当输入的未知扰动信号F(t)=-3sin(0.8t),从图中可以看出,在0到1 s处,出现较大的抖动。分析可知,开始时,在未知扰动F作用下,z轴的实际值与z轴目标值偏差较大,在γ的作用下放大12倍;随着时间推移,通过自适应滑模控制律的调节,偏差逐渐缩小。从图中可以看出,z轴子系统的z轴实际值在这个估计值Fp的作用下,通过调节偏差,在2 s后到达滑模面,可以使系统达到稳定。由于自适应滑模控制律中含有符号函数的缘故,到达滑模面之后会出现抖振,可以通过滤波方法、观测器方法等控制方法来削弱抖振[9]。

4 结论

本文针对四旋翼非线性的数学模型,借助李雅普诺夫稳定性定理构造反步法滑模控制器。控制器设计完成之后,需要对其进行李雅普诺夫稳定性定理的验证,证明其系统的稳定性。仿真试验验证了控制器的效果。最后对滑模控制算法特有的优点进行了理论分析,并进行仿真试验,验证其对有界扰动具有很好的鲁棒性。