基于超单元法的无铰式旋翼桨毂动力学等效参数计算方法

邱志祥,喻国瑞,王伟特

(中国直升机设计研究所,江西 景德镇 333001)

0 引言

旋翼动力学分析中的动力学参数即为结构的力学参数。将旋翼简化为梁模型的经典气弹分析方法中,需输入桨叶剖面特性、桨毂剖面特性和操纵线系刚度等参数。

无铰式旋翼动力学特性对桨毂剖面特性较为敏感,同时桨毂支臂中多采用金属轴承,包含复杂的接触和约束问题,旋翼动力学建模时采用面积分的桨毂结构剖面特性参数会造成旋翼动力学计算结果偏差较大。国外在处理类似桨毂支臂梁模型参数时,通过引入三维有限元思想,获取桨毂支臂等效刚度特性[1]。

本文提出一种计算桨毂等效动力学参数的计算方法:首先对静力缩聚超单元法等效计算桨毂支臂动力学参数开展理论分析,推导等效刚度计算公式和误差;其次基于实际模型,对桨毂支臂进行三维有限元建模,给出轴承的简化处理办法,开展模态分析,验证静力缩聚超单元法的可行性;最后对桨毂支臂进行三维有限元静力分析,根据分析结果,对三维结构进行缩减,获取桨毂支臂挥舞刚度和摆振刚度两个动力学参数。旋翼旋转动特性试验结果表明,该等效方法计算精度满足工程所需。

1 超单元基本理论推导

超单元法是将各子结构内部自由度缩聚到边界自由度上,然后将子结构的独立边界自由度进行组合求解。常用的超单元法分为三种:静力变换超单元法、定频动力变换超单元法、模态综合超单元法[2-3]。其中,静力变换超单元法强制忽略了内部自由度,会导致高阶振动分析产生较大误差。当关注的频率成分远小于子结构模态频率,静力变换超单元法可大大降低模型分析的复杂度。图1为子结构示意图。

图1 子结构示意

如图1,假设子结构1是复杂结构,内部多路传力,且包含非线性接触约束,不能直接看成单梁结构。使用有限元技术,将结构离散,设总共有N个自由度。将N个自由度进行区分,分成子结构1边界上的自由度(下标m)和非边界上的自由度(下标s)。则可以将子结构1的动力学方程写为:

⑴

对上述时域方程做傅里叶变换,可写为频域传递矩阵表达式:

(2)

根据上式有:

DsmXm+DssXs=0

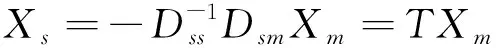
(3)

将式(3)带回式(2),可得

(Dmm+DmsT)Xm=Fm

令:P=Dmm+DmsT

由此可将式(1)变换为

PXm=Fm

(4)

上述为超单元法的基本理论,式(4)称为超单元方程,P为超单元动力矩阵。根据该基本理论,为完全等效不具有梁特性的子结构1(桨毂),就需要通过桨毂的三维实体,建立有限元模型,再生成2节点超单元梁模型即可。

将超单元方程转换至模态坐标系(Φ为模态振型,ξ为模态坐标),此时子结构动力学方程如下:

ΦT(K-ω2M)Φξ=ΦTFm

(Kdiag-ω2Mdiagξ=Fξ

(5)

结构固有频率

(6)

最终动力学方程描述如下

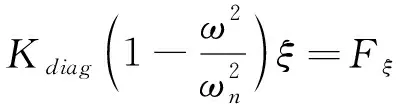
(7)

本文所采用的静力缩聚超单元法,是在局部柔性不突出的情况下,子结构最低阶模态固有频率远大于外载激励最高频率。此时P可退化成刚度等效矩阵,因此超单元法的实现流程可转化为对桨毂支臂整体静刚度的等效过程。图2给出了基于上述超单元法理论制定的获取桨毂动力学参数的技术路线。

图2 桨毂动特性参数获取技术路线

2 桨毂支臂三维有限元分析

图3给出了某万向铰旋翼桨毂支臂示意图,桨毂支臂由桨叶连接件、轴颈螺母、三组轴承和桨毂中央件组成。离心力沿桨叶连接件、轴套螺母、铰接触轴承3、推力轴承2、深沟球轴承1、轴颈螺母、中央件支臂路径传递(图中轴承区域,黑色代表滚珠,同色两部分结构分别代表轴承内外圈)。弯矩传递路径有两条:一是通过轴承1和轴承3的剪力承担,二是通过轴承2轴向非均布压力承担。

2.1 三维有限元建模

经过分析桨毂支臂传力路径方式,保留其承力主体结构,包括桨毂中央件、桨叶连接件、三个轴承以及相应两端的紧固件。

实际轴承包含内圈、外圈、滚动体等承力组件,滚动体和内外圈之间满足Hertz接触理论,可通过三维有限元建立轴承详细分析模型[4-5]。但上述轴承模型复杂,不适合桨毂支臂整体分析。本文关注桨毂支臂整体刚度特性,不关注轴承局部受力情况,为提升建模和计算效率,给出了一种轴承简化处理办法。图4给出了轴承简化模型,滚动体简化为圆柱形实体结构,圆柱侧面积为轴承滚道投影区域。根据轴承传力特征,滚动体等效结构一侧与轴承内圈或外圈融合,另一侧设置摩擦接触约束。图5给出了轴承内外圈与桨毂支臂内部其他相邻结构的约束关系,根据传力特征分别选择Tie约束或者接触摩擦约束。在桨叶连接件衬套孔中心施加弯矩,固支约束桨毂中心,最终有限元模型如图6。

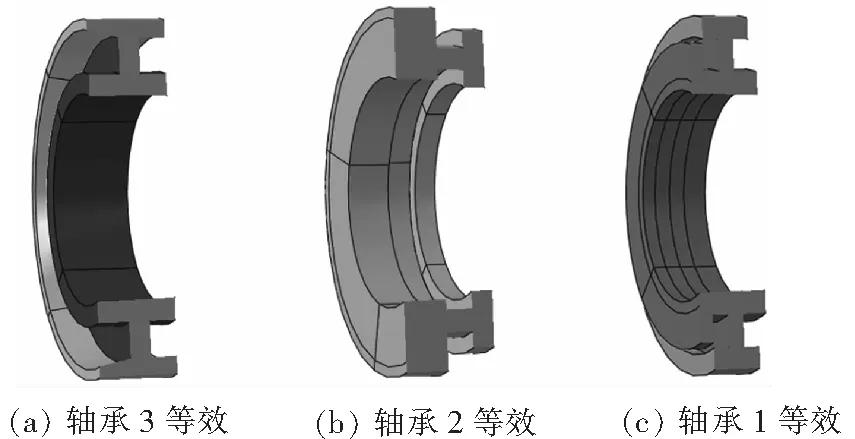
图4 桨毂支臂内部轴承等效建模

图5 桨毂支臂内部接触约束示意图

图6 桨毂三维有限元模型

2.2 固有频率计算

图7给出了上述桨毂支臂三维有限元模型模态分析结果,挥舞一阶频率24.92Ω,摆振一阶频率32.67Ω。

图7 桨毂支臂模态分析结果

旋翼动力学设计关注前8阶谐波影响。固支边界条件下,将桨毂支臂整体静刚度等效为动力学参数,子结构简化分析误差:

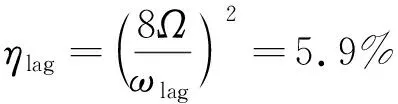
(8)

计算结果表明,挥舞一阶频率最低,等效刚度最大误差为10.3%。

2.3 静力分析和动力学参数等效

在上述桨毂支臂三维有限元模型的基础上,对桨毂支臂进行静刚度分析,计算出桨叶连接位置加载点处的变形θflap和θlag。采用静力缩聚超单元法计算出的桨毂支臂等效挥舞刚度与摆振刚度如下:

(9)

图8给出了传统面积分法和静力缩聚法得到的桨毂刚度对比。可以看出,由于面积分是简单将剖面各结构的刚度叠加,类似将结构视为并联传力,其计算的剖面刚度远远大于静力缩聚计算结果。

图8 面积分法(实线)和静力缩聚(虚线)得到的桨毂刚度对比

3 旋转动特性试验验证

3.1 旋翼动特性计算

建立旋翼CAMRAD II计算模型,开展动特性计算。为简化模型以适用于工程设计,将万向铰模型的桨根约束边界等效为固支边界和铰边界,前者对应挥舞集合型模态,后者对应挥舞周期型模态。对于3片桨叶万向铰旋翼,挥舞集合型模态避开3、6、9……等桨叶片数整数倍谐波频率,挥舞周期型模态避开1、2、4、5、7、8……等非桨叶片数整数倍谐波频率[6]。

表1是中立总距、额定转速状态各阶模态频率比。计算结果表明,除挥舞周期型耦合一阶相近,静力缩聚法得到的其他各阶模态频率比都明显小于面积分法。图9是挥舞周期型共振图。结果表明,两种方法挥舞周期型耦合二阶模态与2Ω的共振点分别为85% RPM和63% RPM。

表1 中立总距状态,旋翼动特性计算结果

图9 孤立旋翼动特性(挥舞周期型)

3.2 旋转动特性试验

开展旋转动特性试验,通过发动机启停识别工作状态主旋翼模态[7]。图10给出了桨叶不同剖面站位处挥舞贴片信号中二阶谐波成分随转速的变化规律,结果表明在65%额定转速附近存在共振。结合图11挥舞周期型耦合二阶桨叶振型图以及旋翼共振图,判断该共振为挥舞周期型耦合二阶与2Ω重合导致。试验结果与静力缩聚计算结果(63%额定转速)吻合,说明了使用静力缩聚计算桨毂动力学参数的有效性。

图10 旋翼桨叶不同剖面挥舞信号二阶谐波幅值随转速变化

图11 挥舞周期型耦合二阶桨叶振型图

4 结论

本文给出了无铰式桨毂支臂动力学参数的一种基于超单元法的静力缩聚等效计算方法。核心是当桨毂支臂局部模态频率远大于关注的外载激励最高频率时(弹性力影响远大于惯性力),可将结构刚度阵近似为超单元动力矩阵。该方法可以将包含复杂摩擦、接触问题的三维桨毂支臂,通过三维有限元分析等效为一维梁,快速得到满足工程使用的桨毂动力学参数。

该方法还可推广至无轴承旋翼桨毂和其他类似非单梁复杂传力构型桨毂上,为获取更加准确的桨毂动力学参数提供了一种新思路。