智能旋翼H∞与CTHHC减振控制算法对比研究

朱棣文,胡和平, 张仕明

(中国直升机设计研究所 直升机动力学全国重点实验室,江西 景德镇 333001)

0 引言

直升机的振动直接影响飞行员、机组人员和乘客的舒适度,并对机械、结构和电子部件的疲劳寿命有很大的影响。因此,直升机振动的抑制问题一直是直升机技术研究的重点[1-3]。

旋翼是直升机振动的主要来源。主动控制后缘襟翼(ACF)技术是通过驱动靠近桨尖位置的后缘襟翼偏转来产生附加的非定常气动载荷,结合一定的控制律,改变桨叶上的气动升力和力矩,从而抵消旋翼本身的激振力,达到减振降噪的效果。ACF具有高带宽、驱动功率小、输出位移大、质量轻及体积小等优势。此外,后缘小翼控制系统与自传倾斜器完全分开来,即使失效也不会明显影响直升机的适航性。

控制算法是主动控制技术的核心之一,好的算法是实现主动控制技术不可缺少的一部分。基于1972年McCloud和Kretz[4]等人提出的旋翼系统响应是线性、准静态的概念,发展出了早期主动控制DTHHC控制算法[5-11]。MIT的Steven Hall[12-13]通过简单地消除采样和保持结构,即可得到连续时间域控制器。CTHHC作为一种连续时域控制算法,可大幅加快控制更新速率,具有更佳的控制性能,并可以提升减振控制器对直升机飞行状态变化的适应性。欧洲直升机公司和斯图加特大学飞行力学和飞行控制研究所[14](IFR)选择采用半经验时域控制和H∞控制执行减振和提高旋翼稳定性等同步控制任务作为研究方向,并在2005-2006年在EC-145上进行了两次飞行试验,实现了4Ω桨毂载荷的显著降低。

国内主要是南航和中国直升机设计研究所[15-18]在进行相关方面的研究,但大多数集中在模型旋翼试验研究阶段。随着计算机计算能力、仿真验证以及控制方法的发展,现在也衍生出了更多种类的控制算法,而不同控制算法的优缺点也成为了研究人员们关注的焦点。

1 控制模型

验证不同控制算法的控制效果首先要确定一个控制模型。针对控制仿真,首先建立智能旋翼的参数化系统模型。为得到模型,首先计算得到4 m直径智能旋翼幅频响应特性数据,随后在MATLAB中辨识得到面向仿真的控制模型传递函数。表1给出了智能旋翼的基本参数。

表1 旋翼基本参数

表2 不同K值下满足要求的时间

可得系统传递函数格式如下:

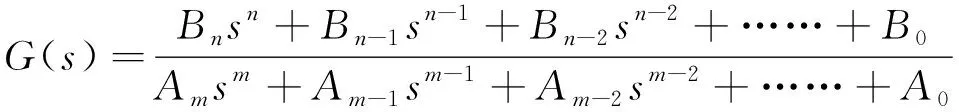
(1)

其中,n和m分别为传递函数分子和分母的阶数。

通过设置襟翼偏转角度,在专用计算软件CAMRADII中获取对应的桨毂载荷作为需要抑制的控制扰动。这里只选取垂向力Fz(所有数据计算均在前飞配平状态下完成)。

图1为频响数据与辨识的参数化模型的拟合程度。由图可见,拟合程度达到86.84%,验证了参数模型的可靠性。

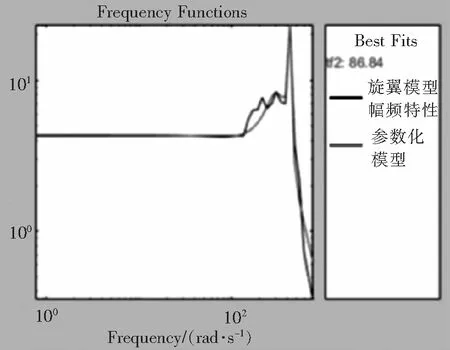
图1 辨识Fz数据结果的拟合程度

2 主动控制算法

2.1 H∞控制算法

在H∞控制方法中,所有的鲁棒控制问题可以表示为如图2形式。

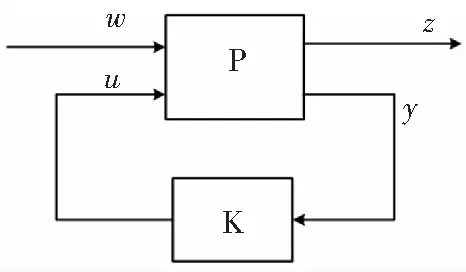
图2 标准H∞控制方法框图

假设P是目标系统,y表示实际输出。K为控制器,此处代表H∞控制器,u为控制输出。上述是传统反馈控制的基本参数。w代表外部输入,表示作用于系统的扰动或参考信号,输出z是系统的外部输出。

在H∞方法中,使用的模型不再只是系统本身,而是一个扩展的模型,见图3。系统的输出不再是y,还包括控制输入u与跟踪误差e加权后的值,根据这输出来设计权重函数W1,W2,W3。

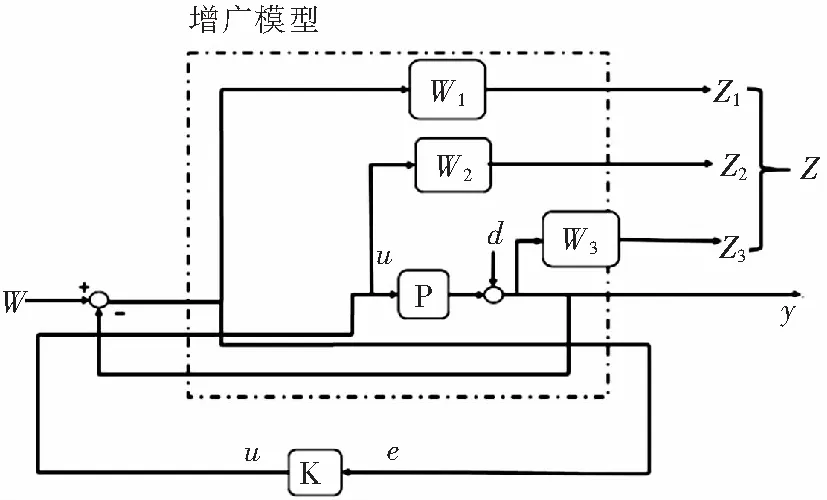
图3 混合灵敏度控制模型

[Z1,Z2,Z3]为一组,代表误差、控制输入、系统输出经过加权(W)之后的值。d代表要抑制的扰动。

对于给定的广义被控对象G(s),判定是否存在反馈控制器K(s) 。令外部输入到输出响应的传递函数表示为Fl(G,K),如果存在使得闭环传递函数内部稳定,且 ‖Fl(G,K)‖∞≤1这样的控制器,则求之,这就是一个H∞标准设计问题。若其无穷范数最小则是H∞最优,满足条件的解控制器是最优控制器,求解需要满足以下条件:

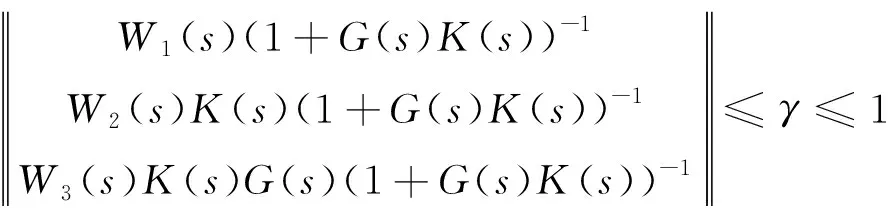
(2)

2.2 H∞最优控制具体设计

整体控制器设计与仿真流程主要步骤如图4所示。

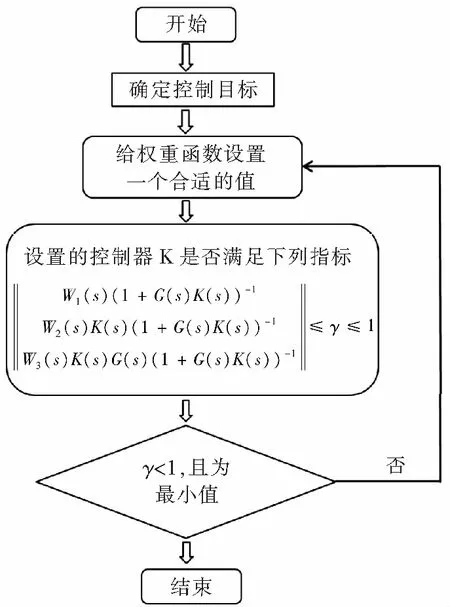
图4 H∞控制器设计流程图

最后确定的权重函数为:

W2=3

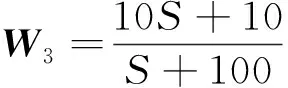
(3)

设计出的权重函数与灵敏度函数、补灵敏度函数奇异值关系如图5-图6所示。

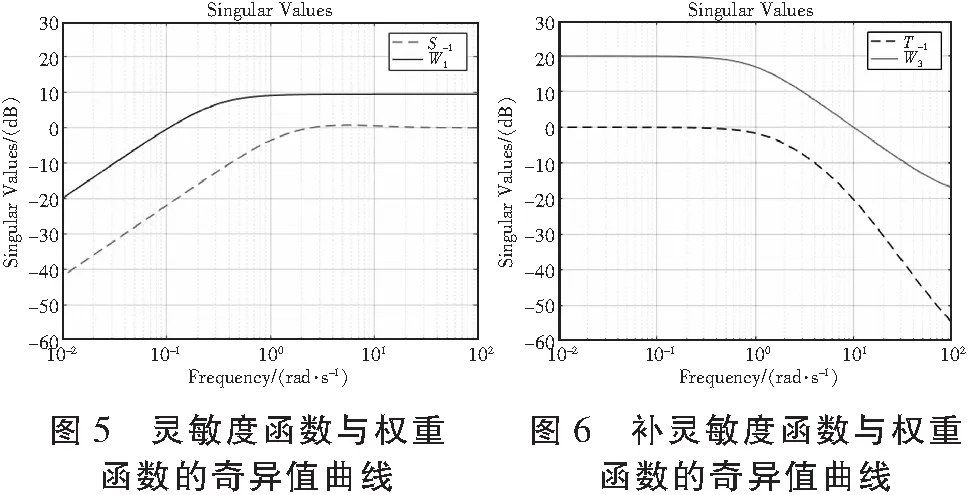
如图可以看出两者的最大奇异值:

(4)

那么可以推出满足:

(5)

则

(6)

即满足条件,设置的控制器符合要求。

2.3 CTHHC控制算法

频域HHC方法由Shaw提出,基于控制输入u消除z0的思想。由于扰动输入z0未知(很可能随时间变化),该方法采用每一时间步测量一次振动水平,调整控制输入以便刚好消除扰动。控制为(频域HHC局部模型):

zn=Tun+z0

zn+1=Tun+1+z0=0

un+1=un-T-1zn

(7)

控制响应矩阵逆,T-1为

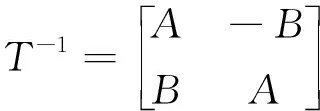
(8)

其中,

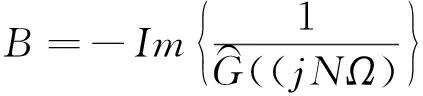
(9)

该控制律将在一个时间步完全抑制扰动。控制器框图如图7所示。前向回路包含静态对象模型T,其中一个扰动波形d(t),加入了对象输出以便得到测量的振动z(t)。测量值首先乘以N/rev频率的正弦和余弦。时变正弦、余弦分量通过一个初始条件为0的积分因子,对一个采样周期进行积分,得到振动的正弦和余弦分量Zs(t)和Zc(t)。信号通过逆矩阵T-1,得到合适的控制增量Δus(t)和Δuc(t),然后加上上一步的控制向量,得到当前采样步的控制向量。最后us和uc乘以cosNΩt和sinNΩt调节,得到控制指令:

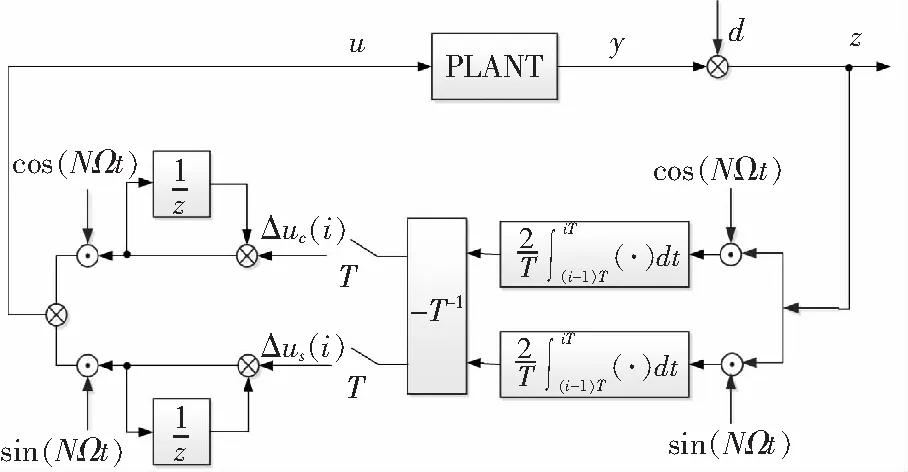
图7 Shaw提出的HHC控制系统

u(t)=uccosNΩt+ussinNΩt

(10)

通过观察,图7可简化为:

u(i)=Δu(i)+Δu(i-1)+Δu(i-2)+…=

-T-1{z(i)+z(i-1)+z(i-2)+…}=

(11)

引入积分因子,得到一个简单的控制系统结构如图8所示。

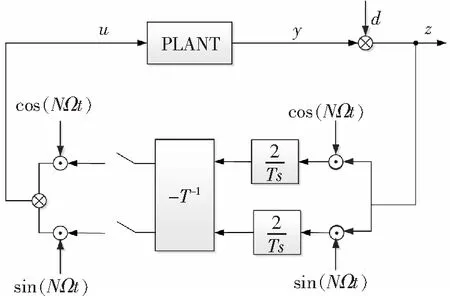
图8 HHC控制系统离散-时间表示方式

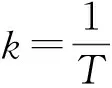
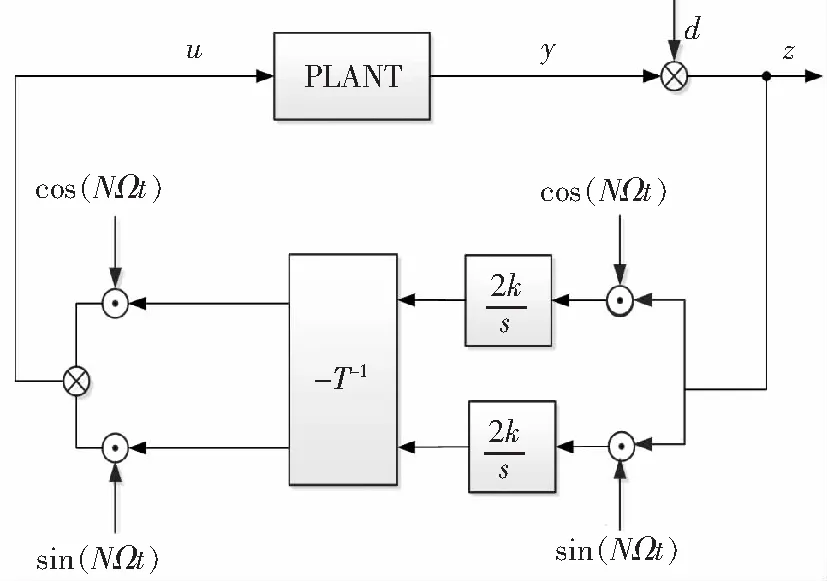
图9 高阶谐波控制连续时间方式(CTHHC)

2.4 CTHHC控制参数设置

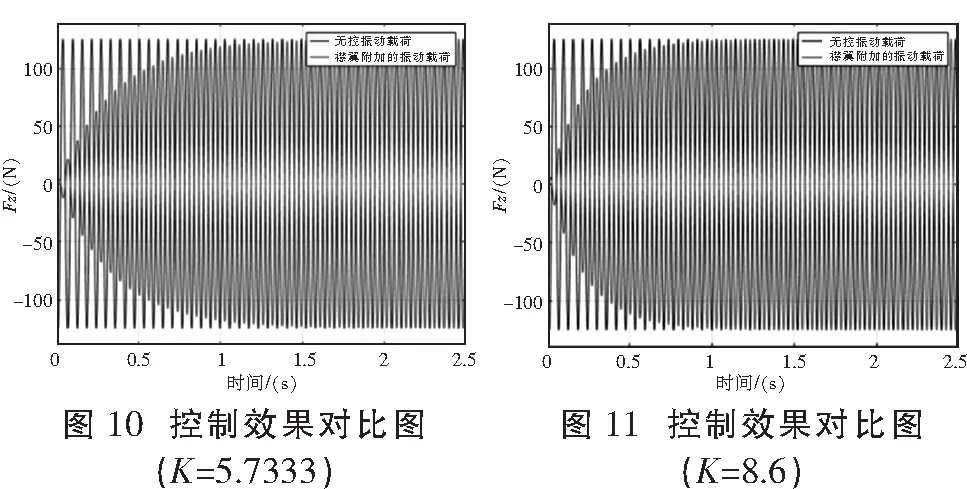
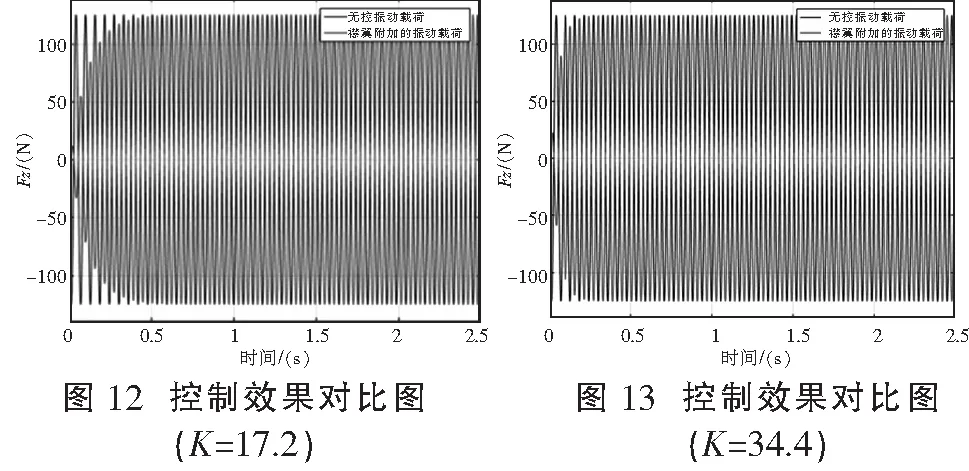
控制器控制系统的控制效果主要由增益系数k决定。令K=2k,则控制器的收敛速度与稳定裕度主要由控制参数K调节。对比不同控制参数K的取值,选取最合适控制模型减振的控制参数。

K的值通常取整周期的倍数的倒数。这里对比4个不同的K取值:

可以发现,K的取值越大则控制量通过襟翼施加的附加载荷能越快地满足对无控振动载荷同幅值反相位的要求,即更快达成控制目标。但出于系统稳定裕度的考虑,不能盲目追求更快的控制效果,故在这里取一个折中合适的参数,即K=8.6。

3 控制仿真结果对比

为了验证两种控制器设计方案的有效性,须确认仿真控制回路模型的准确性,进而对比两种不同方法的性能。因此,基于前文通过频响数据辨识出的同一个控制模型,对比针对桨毂4Ω载荷垂向力F4Z的控制效果(见图14、图15)。

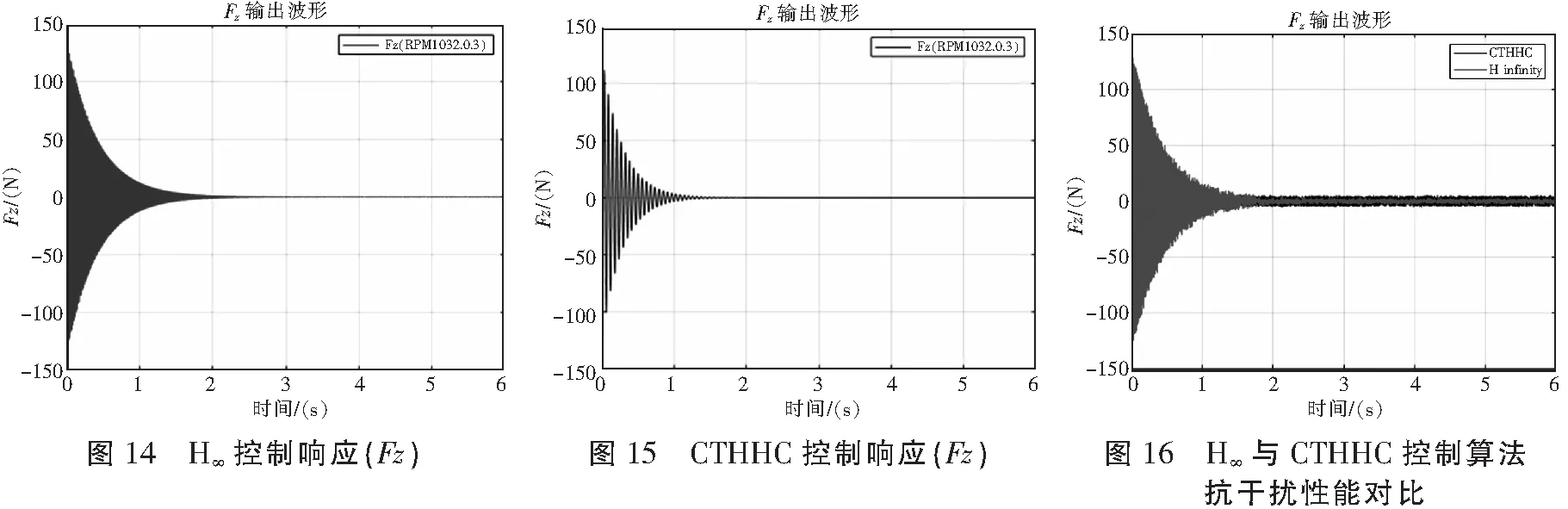
图14 H∞控制响应(Fz)

可以看到,CTHHC在1.5 s左右就已经基本收敛,而H∞控制响应要等到2.5 s左右才能基本收敛,CTHHC在控制响应速度方面的表现显著优于H∞控制。

控制器在实际运行时,不可避免地存在信号干扰。在2个不同控制器的传递框架内施加一个相同的信号干扰,对比其对于控制回路中的干扰的抑制效果,见图16。

由图可见,H∞控制与CTHHC在施加的干扰下都能很好地抑制桨毂载荷,但H∞控制对于外部扰动的抗干扰能力较强,能更好地对外界扰动做出抑制,更精确地达成控制目标。

4 结论

1)针对4 m直径ACF旋翼,在旋翼转速达到额定转速1032 r/min时,旋翼的周期转速是60/1032=0.058 s。从上述分析可以看出, CTHHC只有在取较大的K值时才能满足动态减振需求。

2)仿真结果显示出H∞控制具有优异的抗干扰性能,能更好地针对外界扰动精确达成期望的控制目标;另外,不管什么控制算法,控制参数的选取都会对控制响应结果起到决定性影响,需要在试验前提前调试,确定最优控制参数。