输入饱和下多航天器分布式固定时间输出反馈姿态协同控制

许闯，吴宝林

哈尔滨工业大学 卫星技术研究所，哈尔滨 150001

在航天器编队任务中，航天器姿态协同控制是至关重要的技术之一。航天器姿态协同控制是指通过控制使编队中的所有航天器姿态趋于一致。按航天器编队结构，航天器姿态协同控制方法可以大致分为以下几种：主从方法、虚拟结构方法和基于行为方法。主从方法结构简单，易于实施，但它是一种集中式结构，一旦主航天器出现故障，那么整个航天器编队就将无法正常工作。Dimarogonas等［1］针对多智能体或者多航天器系统，基于主从方法提出了一些姿态协同控制策略。在虚拟结构方法中，整个航天器编队将被视为一个虚拟的刚体，然后针对这个虚拟的刚体设计控制策略，最终实现控制目标［2-3］。文献［4-8］基于虚拟结构方法设计了一些航天器姿态协同控制策略。基于行为方法将根据编队控制任务的各种事件的权重，来设计控制权重函数。然后，根据这个权重函数来设计控制器。这种方法是一种分布式控制方法，比较灵活。但是，基于行为方法很难描述系统的整体行为。针对多航天器姿态存在外界干扰、模型不确定或者航天器间通信带宽受限等问题，文献［9-14］基于行为方法设计了一些航天器姿态协同控制策略。

收敛时间是系统的一个十分关键的性能指标，它们通常被用来描述系统响应的所需规格和性能要求。近年来，为了满足对系统响应时间和鲁棒性的要求，研究人员提出了很多种控制方法，例如有限时间控制方法和固定时间控制方法等。有限时间控制可以保证系统状态在一个有限的时间内到达平衡点。相比于传统的渐近稳定控制，有限时间控制具有更快的收敛速度，更快的收敛速度通常意味着闭环系统具有更好的抗扰特性［15］。因此，有限时间控制也可以提高整个控制系统的对外界干扰的抑制能力。但是，在有限时间控制中，系统收敛时间的上界不仅仅取决于系统参数，还与系统的初始状态有关。这导致当系统的初始状态远离平衡点时，有限时间控制的收敛时间可能会很长，从而无法满足任务对系统收敛时间的要求。

为了解决上述有限时间控制问题，研究人员提出了固定时间控制这一方法。固定时间控制是一种能保证系统状态在固定时间内收敛到平衡点的控制方法，其收敛时间的上限是一个只与系统参数有关的正常数［16］，与系统初始状态无关。固定时间控制与有限时间控制类似，它相当于有限时间控制的进一步延伸。与有限时间控制相比，固定时间控制的收敛时间不依赖于系统的初始状态。不管系统的初始状态如何，固定时间控制的收敛时间上界都是固定的。因此，相比于有限时间控制，即使当系统的初始状态远离平衡点时，固定时间控制的收敛速度也会很快。此外，固定时间控制方法不仅明显提高了系统收敛速度，而且还保留了有限时间控制方法的高鲁棒性，具有很高稳态精度和很强抑制干扰能力。目前固定时间控制方法可大致归类为：终端滑模方法［17-21］、加幂积分方法［22-24］和齐次性理论方法［25-28］这3种方法。终端滑模固定时间控制方法是基于Lyapunov固定时间稳定性定理得到的，设计过程简单，证明思路清晰，并且很容易与自适用控制和干扰观测器方法结合来处理存在扰动和不确定项的系统，因此这种方法应用地最为广泛。加幂积分固定时间控制方法是连续非光滑控制方法的一种，具有很好的抗干扰性能。齐次性理论固定时间控制方法是基于双极限齐次性定理来证明系统的固定时间稳定性，它的证明思路也较为清新，同样具有很好的抗干扰性能，但是证明过程相对复杂一些。因此，目前基于齐次性理论固定时间控制方法的研究成果相对较少。这3种方法在控制器设计上并无本质区别，主要区别在于系统的稳定性证明中。因此，这3种方法的控制性能相差无几。

在实际的太空应用中，航天器的姿态执行机构的输出力矩是有限的。如果在设计控制策略时没有考虑这个问题，很可能会导致系统收敛时间预估的不准确，更为严重的话甚至会导致系统失稳。此外，在航天任务中，角速度敏感器陀螺可能会出现故障。在这种情况下，系统将无法获得角速度测量值，这时基于角速度测量值的姿态协同控制策略将无法使用。据我们所知，现如今还没有同时考虑这2个约束的航天器固定时间姿态协同控制成果。因此，研究输入饱和下无需角速度测量的多航天器分布式固定时间姿态协同控制问题是很有必要的。

基于以上讨论，本文研究存在航天器执行机构饱和与无角速度测量问题下多航天器分布式固定时间姿态协同控制问题。为了解决只有部分航天器可以获得主航天器姿态和角速度状态信息问题与航天器自身无角速度测量问题，设计固定时间的主航天器状态观测器和固定时间航天器角速度观测器，来分别在固定时间内估计出主航天器状态信息和航天器自身角速度信息。然后，基于估计的主航天器状态信息和航天器自身角速度，设计了一个固定时间姿态追踪控制器，并利用齐次性理论证明了闭环系统的固定时间稳定性。此外，本文还进行了数学仿真来验证所提控制策略的有效性，主要创新点如下：

1）针对有向航天器编队通信结构，设计了一个固定时间主航天器状态观测器，来在固定时间内观测出主航天器的姿态和角速度信息，解决了航天器编队种只有一部分航天器可以获得主航天器状态信息问题。

2）设计了一个固定时间航天器角速度观测器，该观测器可以保证在固定时间内观测出航天器角速度信息。

3）提出了一种考虑输入饱和问题的固定时间航天器输出反馈姿态协同控制策略。在该策略作用下，无需角速度测量信息，所有航天器姿态可以在固定时间协同追踪上主航天器姿态轨迹。

1 基础理论

1.1 航天器姿态运动学与动力学

第i个航天器的姿态运动学与动力学方程为

式中：qi=[qi1，qi2，qi3]T∈R3为修正的罗德里格斯参数（Modified Rodrigues Parameters， MRPs）；ωi∈R3表示航天器本体坐标系相对于参考坐标系的姿态角速度；Ji∈R3×3表示航天器的转动惯量；ui=[ui，1，ui，2，ui，3]T∈R3为航天器指令力矩；

对于向量x=[x1，x2，x3]T，x×∈R3×3定义为

若将式（2）用MRPs来表示，则航天器执行机构输出力矩受限下第i个航天器姿态动力学方程可以写为

式中：

定义主航天器的姿态及其角速度分别为q0和ω0，则有

定义姿态追踪误差为

1.2 代数图论基础

本文用代数图论来描述航天器编队中航天器之间的通信拓扑结构。考虑包含n个航天器的编队，采用有向图G={N，E，A}表示各个编队成员之间的通信拓扑，其中N={n1，n2，…，nn}是一个有限非空的节点集合，E⊆N×N是由不同边组成的集合，边(ni，nj)表示节点nj可以从节点ni获得信息。A=[aij]∈Rn×n是图G的权值邻接矩阵。权值aij定义为：如果(nj，ni)∈E，则aij＞0；否则aij=0。另外，一般假设节点与自身不存在连通性，即aii=0。Ni为航天器ni的相邻航天器集合。Laplacian矩阵L=[lij]∈Rn×n定义为lii=∑j∈Niaij，

将航天器编队的参考姿态视为一个虚拟的主航天器，并标记为第0颗航天器。用图Gˉ来描述包含n个跟随航天器和一个主航天器的编队的通信拓扑结构。定义A0=diag(a10，a20，…，an0) 为图Gˉ的主航天器相对于跟随航天器的权值邻接矩阵。如果第i颗跟随航天器可以获得主航天器状态信息，则ai0＞0，否则ai0=0。

引理1［29］如果图Gˉ包含一个有向生成树并且根节点为主航天器，那么存在一个正定的对角矩阵W使得Z=WH+HTW为正定矩阵，式中：H=L+A0，[w1，w2，…，wn]T=H-T1n，W=diag(w1，w2，…，wn)。

1.3 齐次性理论

本节给出了一些关于齐次性理论的定义及引理。

定义1［30］对于向量x=[x1，x2，…，xn]T∈Rn和r=[r1，r2，…，rn]T∈Rn(ri＞0，i=1，2，…，n)定义其中ε＞0。

定义2［30］对于函数g(x)： Rn→R，如果对于任意x，r∈Rn和ε＞0恒成立，那么则称g(x)是r齐次的，并且齐次度为k。

定义3［30］如果函数f(x)=［f1（x），f2（x），…，的每一个分量fi(x)（i=1，2，…，n）都是r齐次的，且齐次度为k+ri，即对于任意ε＞0和恒成立，那么称f(x)为r齐次的，并且齐次度为k。

定义4［16］对于连续函数g(x)： Rn→R 和连续不为0的函数gp(x)，如果下述条件对于紧集C⊂Rn{0}恒成立，那么函数g(x)关于(rp，kp，gp)是p极限齐次的，其中p=0或者p=∞，rp=[rp1，rp2，…，rpn]∈R+n是权重向量，kp为齐次度，gp(x)为近似函数。

定义5［16］对于连续函数f(x)： Rn→Rn，如果对于kp+rpi＞0，fi(x)关于(rp，kp+rpi，fpi)都是p极限齐次的，则称函数f(x)关于(rp，kp+rpi，fpi)是p极限齐次的， 其中p=0或者p=∞，rp=[rp1，rp2，…，rpn]∈R+n是权重向量，kp为齐次度，fp(x)为近似函数。

定义6［16］若一个函数既是0极限齐次又是∞极限齐次的，则称该函数是双极限齐次的。

考虑如下系统：

式中：x(t)∈Rn为系统状态；f(x)：Rn→Rn为连续函数，并且f(0)=0。将系统的初始状态记为x(t0)，其中t0为系统初始时刻。

引理2［16］对于系统式（13），假设函数f(x) 关于(r0，k0，f0)和 (r∞，k∞，f∞)是双极限齐次的。如果系统ẋ=f(x)和其近似系统̇=f0(x)与̇=f∞(x)是全局渐进稳定的，并且k∞＞0＞k0，那么系统式（13）的平衡点是固定时间稳定的。

引理3［31］定义映射p：(0，∞)×Sn→Rn/{0}为那么p的逆映射q：Rn/{0}→(0，∞)×Sn定义为q(y)=p-1=(qε(y)，qx(y))，可得qε和qx在Rn/{0}上为无穷阶可微函数，并且lim||y||→0qε=0， lim||y||→0qx=∞。

1.4 其他相关引理

引理4［13］设矩阵M∈Rm×m，矩阵N∈Rn×n，那么有：

1）如果矩阵M和矩阵N是对称矩阵，那么矩阵M⊗N也为对称矩阵，⊗代表克罗内克积（Kronecker Product）。

2）设λ1，λ2，…，λm为矩阵M的特征值，μ1，μ2，…，μm为矩阵N的特征值。那么矩阵M⊗N的特征值为λiμj()i=1，2，…，m；k=1，2，…，n。

3）设m=n，并且矩阵M和矩阵N的特征值分别非负数和正数，那么矩阵M+N的特征值为正数。

引理5［18］对于xi＞0 ()i=1，2，…，n，有

引理6［32］对于x，y∈R，如果0＜r≤1，则

引理7［33］对于x，y∈R，如果r1＞0，r2＞0，p＞0，则

引理8［34］对于xi≥0 ()i=1，2，…，n，0＜α＜1＜β，α0∈(μ(1+β0)-β0，1)，β0∈(1，β]，其中μ=(α+β)/(1+β)，有下列不等式成立：

式中：r1=(α0+β0)(1+β0)≤1；r2=2β0(1+β0)≥1。

引理9［33］如果系统式（13）存在连续正定的Lyapunov函数V(x(t))满足下述条件：

1）V(x)=0⇔x=0。

2） dV(x)dt≤-αVp-βVq，其中p＜1，q＞1，α、β、p和q为正常数。

那么系统式（13）的平衡点是固定时间稳定的，其收敛时间上界为

2 主要内容

首先，介绍一些本文将用到的一些合理假设：

假设1航天器的外界干扰力矩di和转动惯量的逆Ji都是有界的，即‖‖J-1idi≤cd，式中：cd＞0为常数。

假设2主航天器姿态一阶导数q0和二阶导数是有界的，即其中cq为正常数。

假设3跟随航天器和主航天器组成的航天器编队的通信拓扑结构含有一个有向生成树，并且有向生成树的根节点为主航天器。

本文的航天器姿态协同控制问题描述如下：

问题1 对于多航天器姿态系统式（5）和式（10），在假设1～假设3基础上，设计一个考虑执行机构输出力矩受限和无航天器角速度测量情况的姿态协同控制策略，使得所有航天器的姿态和姿态角速度可以在固定时间T内跟踪上主航天器的姿态和姿态角速度，即limt→Tqei(t)=0，为控制参数相关的系统收敛时间。

为了解决问题1，本文提出了一种考虑输入饱和的分布式固定时间输出反馈姿态协同控制策略。首先，本文设计了一个分布式固定时间主航天器状态观测器来观测主航天器状态信息。接着，设计了一个固定时间航天器角速度观测器来估计航天器的角速度。然后，设计了一个固定时间滑模面。最后，基于观测器的估计值和固定时间滑模面，设计了一个固定时间输出反馈姿态追踪控制器。

2.1 固定时间主航天器状态观测器设计

在本节的控制策略中，需要用到主航天器的状态信息q0和但是，编队中只有一部分航天器可以直接获得主航天器的状态信息。为了解决这个问题，本节设计了一个分布式固定时间主航天器状态观测器来估计主航天器的状态信息q0和

关于固定时间主航天器状态观测器式（20）和式（21），可以得到以下定理。

定理1对于固定时间主航天器状态观测器式（20）和式（21），如果假设2和假设3成立，并且λ1＞cq，λ2＞cq，那么估计值p1i和可以在固定时间Tob内分别收敛到q0和，Tob为

式中：μ1、μ2、r1和r2为正常数，并且其具体的定义会在后面证明中给出。

证明首先证明估计值p1i可以在固定时间Tob内收敛到q0。

定义如下的Lyapunov函数

式中：χ1i=[χ1i，1，χ1i，2，χ1i，3]T；wi＞0为正定的对角矩阵W的对角元素；W的详细定义请参考引理1。

Lyapunov函数Vq的时间导数为

式中：sig2(χ)=sign(χ)|χ|2。

定义

将式（25）代入式（24）可得

定义

当χ1i，k＜0时，可得ni，k-≥0和ni，knj，k≥0，因此Φi，k≤0。当χ1i，k＞0时，可得ni，k-≤0和ni，k-nj，k≤0，因此Φi，k≤0。当χ1i，k=0时，可得Φi，k=0。综上可得，Φi，k≤0恒成立。

那么，式（26）变为

式中：

估计值p2i在固定时间Tob内收敛到的证明过程与p1i可以在固定时间Tob内收敛到q0的证明类似，按照第一部分类似的证明过程，可得估计值p2i在固定时间Tob内收敛到因此，估计值p1i和p2i可以在固定时间Tob内分别收敛到q0和

2.2 固定时间航天器角速度观测器设计

当航天器角速度测量模块出现故障时，航天器无法测量自身的角速度，因此，本文设计了一个航天器角速度观测器来观测航天器姿态的一阶导数

定义qi和的估计值分别为z1i和z2i。估计误差定义为基于文献［27］，固定时间航天器角速度观测器设计为

估计误差和的导数为

式中：

定义

注意到矩阵M1为Hurwitz矩阵。因此，存在一个对称正定矩阵N1满足M1TN1+N1M1=-I6。构建一个如下的径向无界的函数

根据文献［27，31］，可以得到以下性质：

性质1定义如下函数

式中：ϕ(·)∈C∞(R，R)定义为

2） 存在常数c1和c2使得对于任意

性质2定义如下函数

2） 存在常数c4和c5使得对于任意

性质3存在常数ε∈(0，1)，使得对于任意相对于扩展向量是常数σ2∈(1-ε，1)和任意向量恒成立。

性质4存在常数ε∈(0，1)，使得对于任意常数σ2∈(1-ε，1)和任意向量恒成立。

性质5相对于扩展向量是齐次的，且齐次度为2，并且其中κ2为正常数。

性质6相对于扩展向量是齐次的，且齐次度为2，并且，其中κ4为正常数。

关于观测器式（30），可以得到定理2。

定理2对于多航天器姿态控制系统式（5）与固定时间航天器角速度观测器式（30），如果假设1成立，并且初始状态zi(0)=位于下列集合内

式中：Δ为足够大的正常数，那么观测误差͂可以在固定时间内收敛到区域≤Δz͂i内，Δz͂i的详细定义请见式（51）。

证明证明分为2种情况：案例 1（Vς≥1）和案例2（Vς＜1）。

案例1构建Lyapunov函数=。由性质2，可得当Vς≥1时，≥1恒成立。的时间导数为

根据性质4可得，存在常数ε1∈(0，1)，使得对于任意常数σ2∈(1-ε1，1)和任意向量恒成立。由性质2和性质6可得，存在常数ε2∈(0，ε1)，使得对于任意常数σ1∈(1-ε2，1)和任意向量成立。那么，式（40）变为

由性质2可得，存在常数c6使得不等式恒成立。构建如下集合

当状态zi和yi均位于集合F1内时，存在常数c7使得不等式恒成立。此外，根据假设1可得，存在常数cd使得不等式成立。那么，式（41）变为

式中：参数μ0满足参数μ5满足那么，式（43）可以写为

因此，在紧集F1内，可以在时间Tso1=内收敛到区域≤1内。

由上述分析可知，紧集F1是前不变集合［35］。这意味着当 (zi(0)，yi(0))∈F1时，(zi，yi)∈F1恒成立。

案例2当Vς＜1，可知Vη＜1。构建Lyapunov函数由性质1可得，当Vη＜1时，的时间导数为恒

根据性质3可得，存在常数ε3∈(0，1)，使得对于任意常数σ2∈(1-ε3，1)和任意向量恒成立。 由性质1和性质5可得，存在常数ε4∈(0，ε3)，使得对于任意常数σ1∈(1-ε4，1)和任意向量成立。

接着，按照案例1的证明过程，可得

V1的导数为

式中：参数μ0满足

这意味着V1(͂)可以在时间Tso2=内收敛到下列区域内：

那么，ηi可以在固定时间内收敛到下列区域内：

观测误差͂可以在固定时间内收敛到下列区域内：

综上分析可得，观测误差͂可以在固定时间Tso=Tso1+Tso2内收敛到下列区域‖≤Δz͂i内。

2.3 固定时间姿态追踪控制器设计

在本文中，使用主航天器状态估计值p1i和p2i来替代主航天器状态实际值q0和使用航天器姿态一阶导数估计值z2i来替代航天器姿态一阶导数实际值

定义如式（52）～式（53）所示新的姿态追踪误差：

那么，由和表示的动力学方程为

分布式姿态协同追踪控制率设计为

式中：k1和k2为正常数。

式中：

定义

注意到矩阵M2为Hurwitz矩阵。因此，存在一个对称正定矩阵N2满足MT2N2+N2M2=-I6。构建一个如下的径向无界的函数

构建如下Lyapunov函数

可以证得，存在正常数δ1、δ2、δ3和δ4使得恒成立。

关于固定时间姿态协同控制器式（55），可以得到以下定理。

定理3对于有向通信拓扑结构下的执行机构输出力矩受限的多航天器姿态控制系统式（5），如果假设1～假设3成立，固定时间主航天器状态观测器设计为式（20）和式（21），固定时间航天器航天器角速度观测器设计为式（30），固定时间姿态协同控制器设计为式（55），航天器初始状态位于下列集合内：

式中：Δ1为足够大的正常数，那么姿态追踪误差qei和可以在固定时间内收敛到区域‖qei‖≤Δq̂i和≤Δq̂i+Δz͂i内。

证明与定理2的证明类似，该定理的证明分为2种情况：案例1 (Vς̂i＞1)和案例2 (Vς̂i≤1)。

案例1构建Lyapunov函数因此当Vς̂i＞1时，＞1恒成立。

构建如下集合

在集合F3内，Δui=Γ(ui)-ui是有界的。接着与定理2的证明类似，可得紧集F3是一个前不变集合［35］。当 (qi(0)，zi(0)，yi(0))∈F3时，可以在固定时间内收敛到区域V4()≤1内。

案例2构建Lyapunov函数=可得，当的时间导数为

与定理2的证明类似，可得存在正常数ζ4和ζ5使得式（65）成立：

式中：δ5为正常数。这意味着V3可以在固定时间内收敛到下列区域内：

那么，可以在固定时间内收敛到下列区域内：

追踪误差和可以在固定时间内收敛到下列区域内：

由定理1和定理2可知，估计值p1i和可以在固定时间Tob内分别收敛到q0和̇，观测误差͂可以在固定时间内收敛到区域内。因此，姿态追踪误差qei和可以在固定时间内收敛到下列区域内：

3 仿真结果

为了验证所提出的固定时间姿态协同控制策略的有效性，本文对所提出的控制策略进行了仿真并对仿真结果进行了分析。首先对固定时间主航天器状态观测器式（20）和式（21）进行一些数学仿真，验证了主航天器状态观测器的性能。然后，对所提出的固定时间航天器角速度观测器式（30）进行了仿真，验证了该观测器的有效性。然后，基于固定时间主航天器状态观测器和固定时间航天器角速度观测器的观测结果，对所提出的固定时间姿态协同控制器式（55）进行了仿真，验证了该控制器的有效性。

仿真考虑了由6个航天器和一个虚拟领导航天器组成的编队，航天器间的通信拓扑如图1所示，其中SC-i代表航天器i。在本节仿真中，跟随航天器的初始姿态和初始角速度、主航天器的姿态轨迹、航天器间的邻接权值矩阵、航天器的转动惯量和外界干扰力力矩设置如表1所示。固定时间主航天器状态观测器式（20）和式（21）的初值和参数设置如表2所示。固定时间航天器角速度观测器式（30）的初值和参数设置如表3所示。

表1 航天器仿真参数Table 1 Numerical simulation parameters of spacecraft

表2 主航天器状态观测器仿真参数Table 2 Numerical simulation parameters of the leader spacecraft’s attitude observer

表3 航天器角速度观测器仿真参数Table 3 Numerical simulation parameters of spacecraft state observer

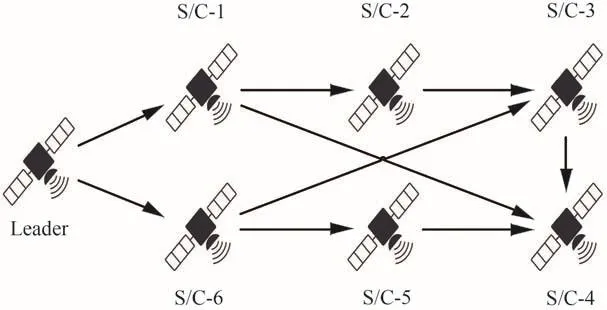
图1 航天器间通信拓扑结构Fig.1 Inter-spacecraft communication topology

固定时间主航天器状态观测器式（20）和式式（21）的观测误差p͂1i=p1i-q0和p͂2i=p2i-q̇0的响应曲线分别如图2和图3所示。由图2可以看出，观测误差p͂1i可以在2 s内收敛到原点附近。在稳定状态时，观测误差p͂1i小于4×10-4。由图3可以看出，观测误差p͂2i可以在1.5 s内收敛到原点附近。在稳定状态时，观测误差p͂2i小于2×10-6。仿真结果表明固定时间主航天器状态观测器式（20）和式（21）具有很快的收敛速度和很高观测精度。

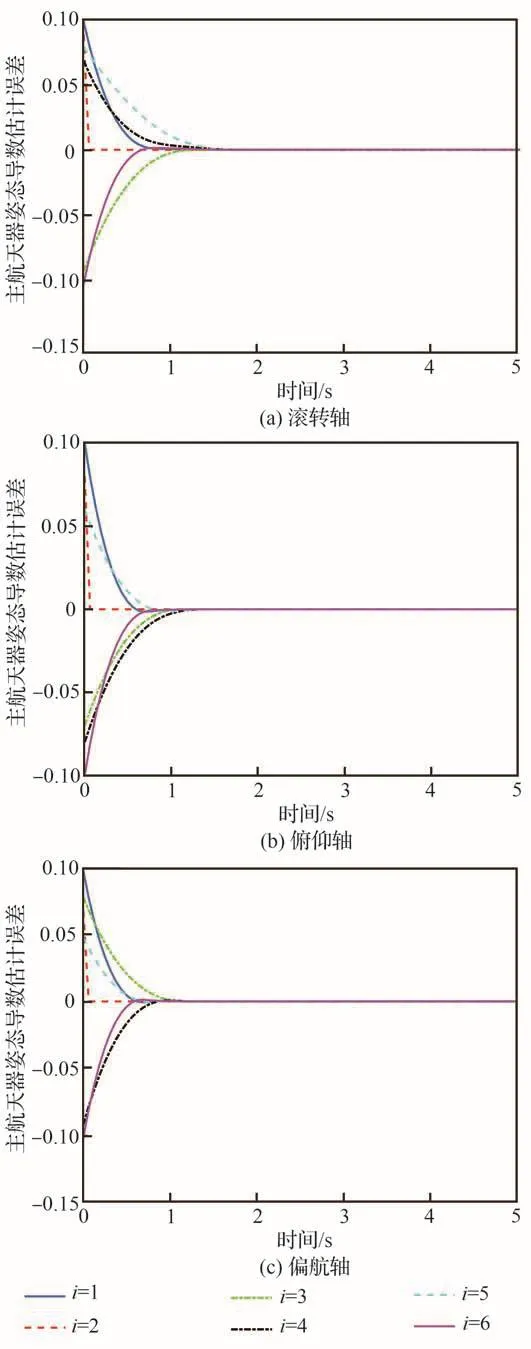
图3 观测器式（21）的误差p2i-q0Fig.3 Errors p2i-q0 by observer in Eq.（21）

图4为固定时间航天器角速度观测器式（30）的观测误差z͂2i。由图4可以看出，观测误差z͂2i可以在3 s内到达稳定状态。在稳定状态时，观测误差小于0.001。该仿真结果证明了所提出的固定时间航天器角速度观测器式（30）的有效性。

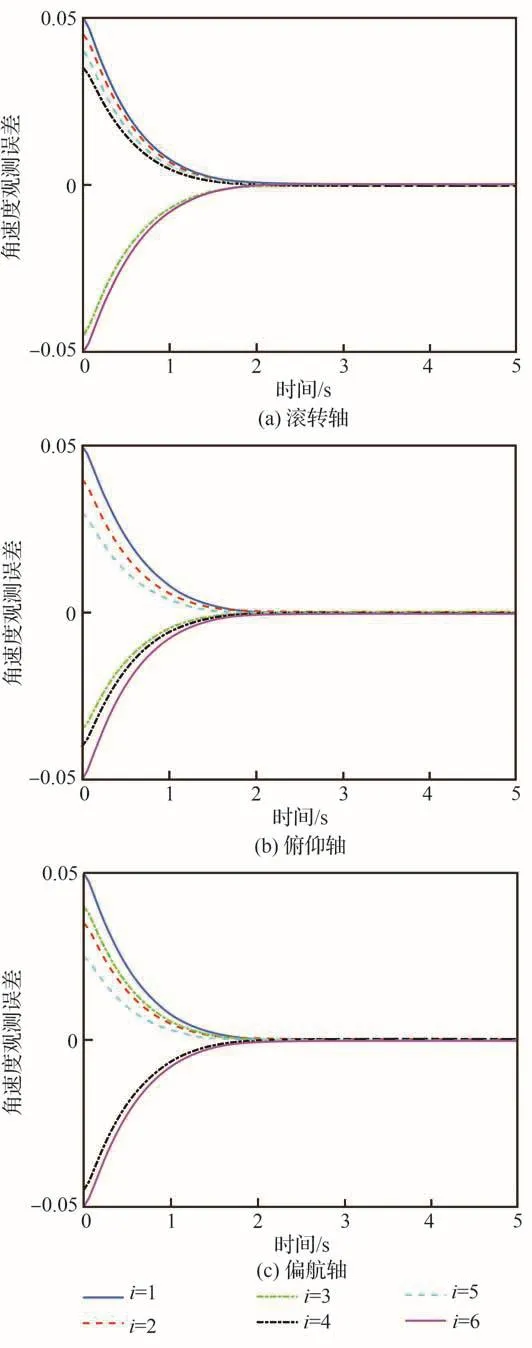
图4 固定时间航天器角速度观测器式（30）的误差Fig.4 Errors in fixed-time spacecraft angular velocity observer in Eq.（30）

在仿真中，固定时间姿态协同控制器式（55）的控制参数设置为k1=0.08，k2=0.4。图5为航天器指令力矩ui的曲线，图6为航天器姿态执行机构实际输出Γ(ui)的曲线。从图5和图6可以看到，尽管航天器指令力矩ui的大小远远超过3 N·m，但是航天器姿态执行机构实际输出Γ(ui)一直保持在3 N·m内，并且当航天器姿态达到稳定状态时，航天器姿态执行机构实际输出Γ(ui)也会相应的变得很小。图7和图8分别航天器姿态追踪误差和角速度追踪误差响应曲线。由图7和图8可以看出，航天器姿态追踪误差和角速度追踪误差可以在30 s内到达稳定状态。在控制器式（55）的作用下，航天器姿态追踪误差和角速度追踪误差的稳态误差分别为0.1°和0.003 （°）·s-1。仿真结果表明在输入饱和与无角速度测量的约束下，固定时间输出反馈姿态协同控制器式（55）仍可以实现很快的收敛速度和很高控制精度。

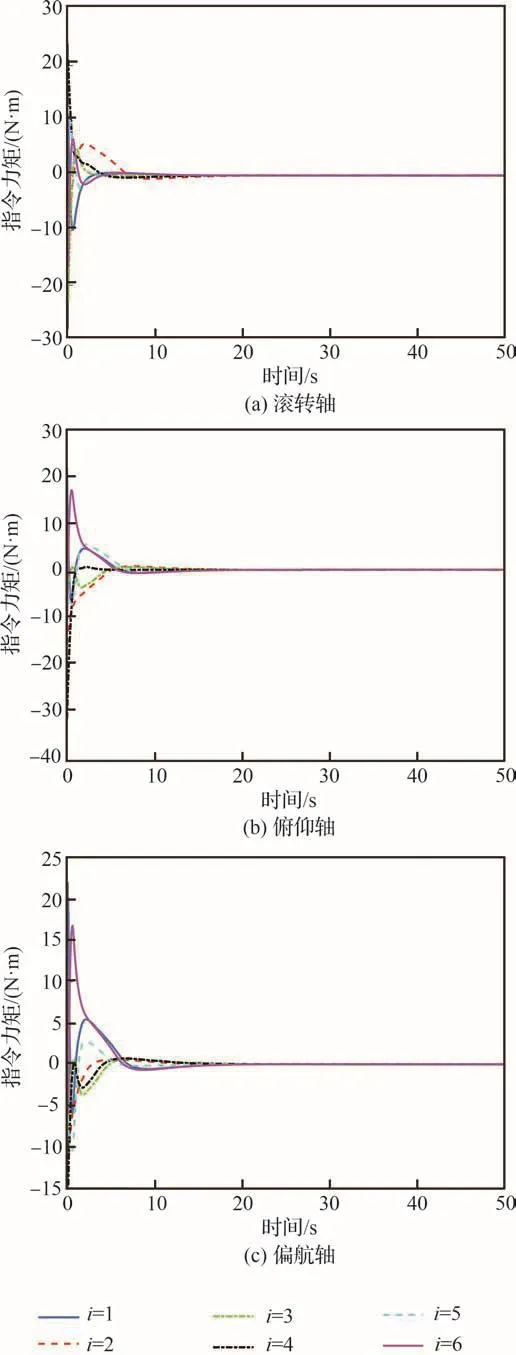
图5 航天器姿态控制指令力矩uiFig.5 Attitude command control torques ui of spacecraft

图6 航天器姿态执行机构输出力矩Γ(ui)Fig.6 Attitude actuator output torques Γ(ui) of spacecraft

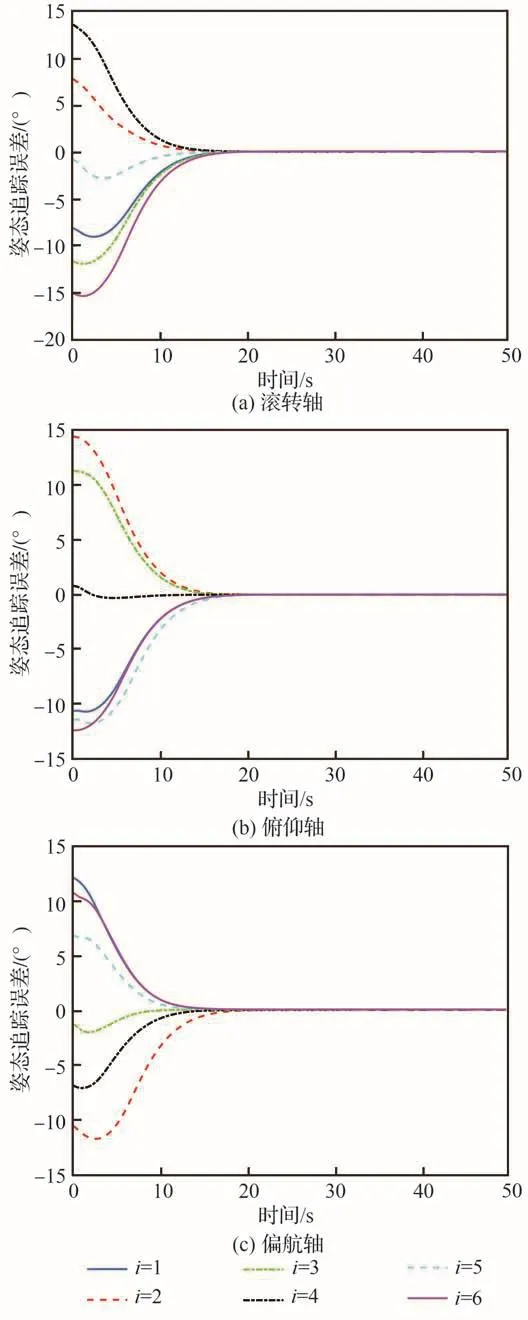
图7 航天器姿态追踪误差Fig.7 Attitude tracking errors of spacecraft

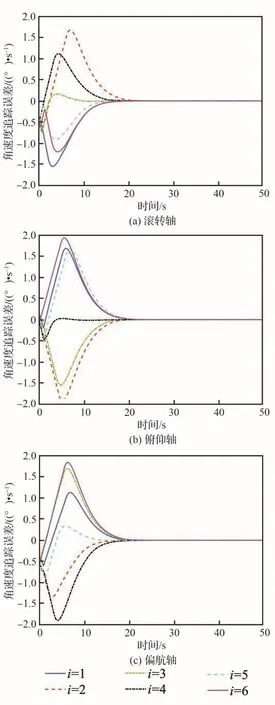
图8 航天器角速度追踪误差Fig.8 Angular velocity tracking errors of spacecraft

此外，本文还将所提出的固定时间控制策略与文献［36］中的有限时间航天器姿态协同控制方法做了对比。为了方便比较，首先定义以下变量来描述系统的控制性能。

式中：Φ(q)表示MRPs对应的欧拉角。

由图9可以看出，与文献［36］中的控制方法相比，尽管本文所提方法在控制初期所需的控制力矩更多一些，但是姿态追踪误差SKM和相对姿态误差FKM收敛速度更快。

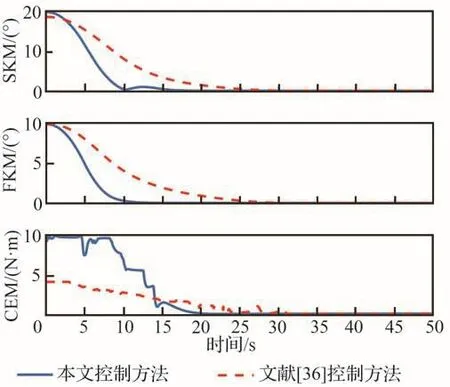
图9 对比结果Fig.9 Comparison results

4 结论

本文研究了存在航天器执行机构输出力矩饱和与无角速度测量情况下分布式多航天器固定时间姿态协同控制问题。本文首先设计了一个分布式固定时间主航天器状态观测器来估计主航天器状态信息。接着，设计了一个固定时间航天器角速度观测器。该观测器可以在固定时间内观测出航天器角速度信息。然后，基于主航天器的姿态信息的观测值和航天器角速度观测器的观测值，设计了一个固定时间航天器姿态追踪控制器，并且证明了整个航天器姿态系统在该控制器作用下是固定时间稳定的。本文还进行数学仿真来验证所提控制策略的性能。仿真结果表明，当航天器执行机构输出力矩存在饱和问题时，本章所提的控制策略可以保证所有航天器的姿态追踪误差可以在固定时间内收敛到一个与输出力矩上界有关的界内。