仿鸟扑翼飞行器气动力学建模精度测试

郑和超，王建辉，胡紫阳，张忠海，何广平，

1.北方工业大学 机械与材料工程学院，北京 100144

2.北京工业大学 材料与制造学部，北京 100124

3.北京航天测控技术有限公司，北京 100041

仿生学和空气动力学研究结果表明，扑翼飞行器在利用涡流能量方面的效果突出［1］，在降低气动噪声、仿生隐藏、抵近侦察等方面优于固定翼和旋翼飞行器，近年来得到国内外研究人员的广泛关注［2-3］。然而由于缺乏系统设计理论，目前试验样机［4-6］的设计制造还主要依靠形态仿生、直觉经验、反复试错和试验修正。关于扑翼飞行器的研究主要包括：驱动机构设计［7］与运动学优化［8］、系统控制［9］及机翼形状和结构参数对气动力特性的影响［4，10-19］等。其中，对驱动机构和机翼结构特性测试和优化是重要的设计基础。研究人员对此也进行了多种尝试，例如，机翼展弦比和偏置角［10］、展向和弦向弱刚度［4，11-16］对扑翼空气动力学的影响、扑翼气动中心的测量方法［20］、扑翼周围气流烟雾的可视化［5］。这些工作主要集中在寻找机翼参数的设计原则或设计指标，相关经验和结论可用于仿鸟扑翼飞行器的设计。

除了试验，通过数值模拟研究扑翼的气动性能也得到了较多关注。例如，Tong等［21］利用涡面场阐明了低展弦比扑翼绕流的涡动力学，并建立了用于估算尾迹中脱落涡面推力模型，但该模型仅适用于尾迹中具有离散涡面的扑翼。Yang等［1］通过数值模拟和试验研究了仿鸽扑翼飞行器的受力机理，利用数字图像动态变形数据分析气动弹性效应和计算惯性力，最终的数值仿真结果与试验结果一致性较好。Chen等［22］利用试验与准稳态和数值模拟研究了仿昆虫微型扑翼飞行器两侧机翼相位差对气动性能的影响，数值模拟结果与试验测得的力和涡量场吻合程度较高。虽然通过数值模拟方法定量预报扑翼产生的气动力，可考虑机翼周围流体状态及机翼表面和空气介质之间交互耦合的作用，但是数值模型的计算往往十分耗时，模拟结果也很难用于对扑翼飞行器的性能优化、闭环控制器设计和系统的运动稳定性分析。

针对以上问题，一些研究人员提出利用解析法预测扑翼飞行器的气动力特性。Lane等［4］采用改进的叶素动量理论方法对扑翼飞行器推力预测，但由于该建模方法未考虑机翼的刚度和材料特性，并没有正确表征机翼的运动学和几何形状，预测的平均推力仅在较高拍动频率下与试验结果基本一致。Nguyen等［10］基于齿轮齿条机构的实测推力，提出了一种预测推力经验公式。该公式考虑了机翼面积、扑动频率、扑动角和机翼展弦比等设计参数，但并未考虑机体姿态角和前向飞行速度等动态飞行参数，因此不能预报扑翼飞行器在实际飞行过程中的气动性能。基于新型测试平台，Mueller等［12］提出了一种预测扑翼飞行器升力和推力的半经验气动模型。该模型考虑了阻力和机翼柔度的影响，但预测结果仅在最低拍动频率下与实测的瞬态气动力相关性较好。年鹏等［23］提出了一种扑动轴瞬时气动载荷半经验高精度建模方法，最终模型确认系数大于0.89，但需基于风洞试验数据建立该模型，不利于扑翼飞行器的广泛研究。Jiao等［24］将一维细长体理论推广，应用于二维平板驱动器的设计，提出了一种通用扑翼周期平均推力的解析估算方法，但这种方法在预报负推力时存在较大计算偏差。

以往相关研究工作表明，在扑翼飞行器气动力预测模型中，需考虑机翼的运动学和几何形状、刚度及其弹性变形，以提高气动力预测结果的准确性。考虑预测模型对样机优化的实际意义，气动力预测模型需具有足够高的计算效率，并考虑扑翼机实际的飞行状态。针对以上问题，提出了一种预测气动力参数化解析计算模型。基于目前实验室已有设备（高速摄像机和三维力传感器），搭建了静态和动态气动力测试平台，测得试验样机在试飞前的气动性能，并明确气动力模型中的机翼几何形状、运动学、变形角、俯仰角和前向飞行速度。与风洞试验相比，该方法可以更低的成本，广泛研究扑翼机的气动性能。为进一步提高气动力预测模型的准确性，基于静态气动力测试数据，修正了传统伪稳态空气动力学的力系数。并将该模型用于预测小型仿鸟扑翼飞行器产生的动态升力，取得了较好结果。

1 弹性平板翼仿鸟扑翼飞行器的气动力学建模

1.1 扑翼机构的运动学模型

扑翼机构运动学如图1所示，“曲柄-滑块-摇杆”机构将曲柄旋转运动转化为摇杆往复摆动，左右摇杆通过齿轮啮合传递动力，与以往的研究［1，4，6，8-13，15，22-24］相比，在结构上更加紧凑，两机翼运动输出具有更好的对称性。并且摇杆输出的拍动近似为余弦运动［16］。当机翼前缘没有展向变形时，相应的拍动角φ0、角速度和角加速度可表示为

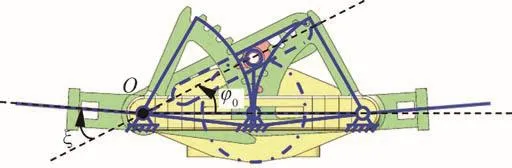
图1 扑翼机构运动学示意图Fig.1 Kinematic diagram of flapping-wing mechanism

本文研究的小型仿鸟扑翼飞行器拍动频率较高、平板翼前缘刚度较小。实际拍动角φ除包含转角φ0外，还需包含由机翼惯性力所导致的展向被动弯曲角ψs［11］。采用静力学分析方法得到弹性平板翼的惯性力FI和展向被动弯曲变形角ψs的关系为

式中：ls为机翼气动中心［9，20］距翼根的距离（见图2）；ks为机翼前缘弯曲刚度；mw为机翼质量；L为机翼前缘长度。

图2 弹性平板翼Fig.2 Elastic flat wing

当拍动振幅A=22°、偏置角ξ=12°、机翼质量mw=0.5 g、机翼前缘长度L=130 mm、平均拍动频率=15.834 7 Hz、机翼前缘弯曲刚度ks=0.3 N·m/rad时，弹性平板翼的运动学规律如图3所示。当考虑展向被动弯曲角ψs后，机翼实际拍动角φ的范围接近51°。

图3 弹性平板翼运动学（T =）Fig.3 Kinematics of elastic flat wing （T = ）

扑翼飞行器的空气动力是由扑翼与流体之间相对运动产生，要建立气动力计算模型，需分析机翼上任意一点的绝对速度［9］。弹性平板翼扑翼飞行器的坐标系如图4所示。∑I代表固定在地球上的惯性系；∑B是固定在扑翼飞行器质心上的机体坐标系；∑W表示附着于机翼根关节的动坐标系；PIC表示机翼质心在惯性系∑I中的位置矢量；PIB是机体质心在惯性系∑I中的位置矢量；PWC是机翼质心在机翼坐标系∑W中的位置矢量；轴xB指向飞行器的前方，轴yB指向机体的右侧，轴zB由左手定则确定；飞行器机体姿态定义为欧拉角α-β-γ；机翼的实际拍动角为φ；弹性平板翼在弦向方向上的扭曲变形角为ψc。为简化坐标系变换，令轴xB和xW始终平行，而当机翼拍动角φ等于0时，轴yB和yW平行。

图4 扑翼飞行器的坐标系Fig.4 Coordinate frames of flapping-wing vehicles

从∑W到∑B，以及从∑B到∑I的旋转变换矩阵分别可写为

机翼质心位置可以表示为

由于向量在机翼坐标系∑W中是不变的，即=0。线速度可表示为

1.2 气动力学建模

在伪稳态空气动力学范畴［9，25］，由流固交互作用产生的气流惯性力是仿鸟扑翼飞行器的主要动力来源，而由流固速度耦合引起的力（如离心力和哥氏力引起的摩擦力）则是次要气动力。在三维空间中，弹性平板翼气动力计算公式［9］为

式中：r为机翼单位长度，dr为沿翼展方向的位置，如图2所示；为机翼在机体坐标系∑B中的绝对线速度矢量(r)和(r)分别为空气动力在机翼坐标系∑W中的法向和切向分力，其方向总是与相反；W(r)为机翼在位置r处的弦宽；ρair=1.205 kg/m3为空气密度；ϕ为机器人的飞行迎角，定义为机翼平面与绝对线速度之间的夹角；(ϕ)和(ϕ)为机体坐标系∑B中的空气动力学系数。

对于实际的飞鸟，可通过控制羽毛姿态以调节翅膀的空气阻力系数［25］，因此即使对于恒定的迎角ϕ，空气动力学系数(ϕ)和(ϕ)通常是时变的。但是，类似昆虫的机翼结构，参考图5，对于弹性平板翼，由稳态经验得到相应的空气动力学系数［9］为

图5 三维空气动力学分析图Fig.5 Diagram for aerodynamics analysis in 3D

式中：φ为机翼的实际拍动角；ψc为机翼在弦向方向上的扭曲变形角。

而式（7）计算出的切向力dfWT(r)为机翼坐标系中表示的实际力矢量。通过式（5）和式（7），机翼的总法向力和切向力沿翼展方向积分表示为

式中：AW为机翼面积为扑翼气动中心在机体坐标系中的绝对线速度。而扑翼在机翼坐标系和惯性系中的总空气动力分别表示为

式中：FB为扑翼飞行器在机体坐标系下的总气动力为从机翼坐标系到机体坐标系的旋转矩阵为从机体坐标系到惯性系的旋转矩阵，由式（3）给出。

根据以往的研究工作［11］，发现在较高拍动频率下，机翼的弦向扭曲变形角主要由柔性机翼上的空气阻力引起。采用静力学分析方法得到弹性平板翼上法向空气动力FzW和被动扭转角ψc之间的关系。相应公式可写为

式中：lc为机翼气动中心距机翼前缘的距离（如图2所示）；kc为机翼的扭转刚度；W为机翼的弦向最大宽度。

根据以往工作测试和计算方法［20］，机翼的扭转刚度kc=0.007 8 N·m/rad。当W=95 mm、机体的俯仰角β=0°、平均前向飞行速度=0 m/s时，利用本节给出的建模方法，小型仿鸟扑翼飞行器两侧机翼在惯性系中所产生空气动力的解析计算结果如图6 所示。两侧机翼在一个拍动周期的平均升力≈-0.000 1 N，平均推力≈0.077 N。由于扑翼飞行器的对称设计，其侧向理论空气动力为0。

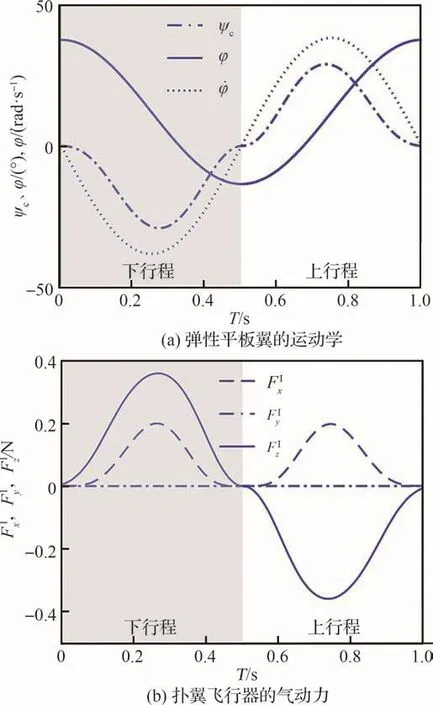
图6 小型仿鸟扑翼飞行器的运动学和气动力（T =）Fig.6 Kinematics and aerodynamic forces of small bird-scale flapping-wing vehicles（T =）

关于小型仿鸟扑翼飞行器的气动力预测和分析，本文仅对以下主要参数开展研究：空气动力学系数（(ϕ)和(ϕ)）、机翼展向的被动弯曲角ψs和弦向的被动扭转角ψc、机翼的平均拍动频率、机体的俯仰角β及平均前向飞行速度

2 扑翼气动力测试系统

2.1 扑翼飞行器及其弹性平板翼

小型仿鸟扑翼飞行器试验样机如图7所示，相应的结构参数如表1所示。为使伪稳态空气动力学模型预测的气动力更具普适性，设计了3 种刚度不同的机翼，如表2 所示。在设计制造试验机翼过程中，为避免不同机翼形状的差异性和安装精度对气动力测试结果造成影响，通过在同一个翼面上增加或者减少支撑碳杆，来保证单纯改变机翼结构的刚度［15］。另外，选用具有较高强度的10 μm厚聚亚酰胺薄膜为翼面，采用直径0.6 mm碳纤维杆作为前缘和骨架。并且碳杆、翼膜和机翼前缘之间都使用20 μm厚透明胶带高温高压粘结。最终，单个试验机翼质量被控制在0.5 g以内，以减小翅膀惯性力对气动力测试结果的影响。

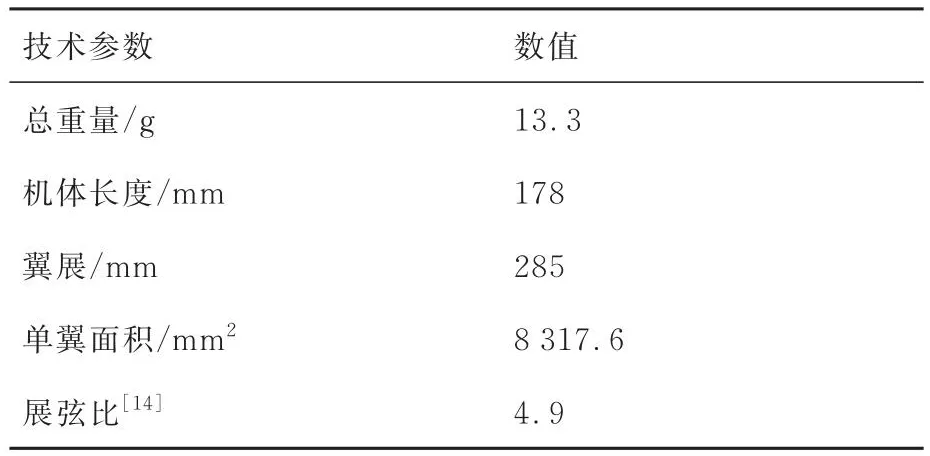
表1 小型仿鸟扑翼飞行器的结构参数Table 1 Structural parameters of small bird-scale flapping-wing vehicles

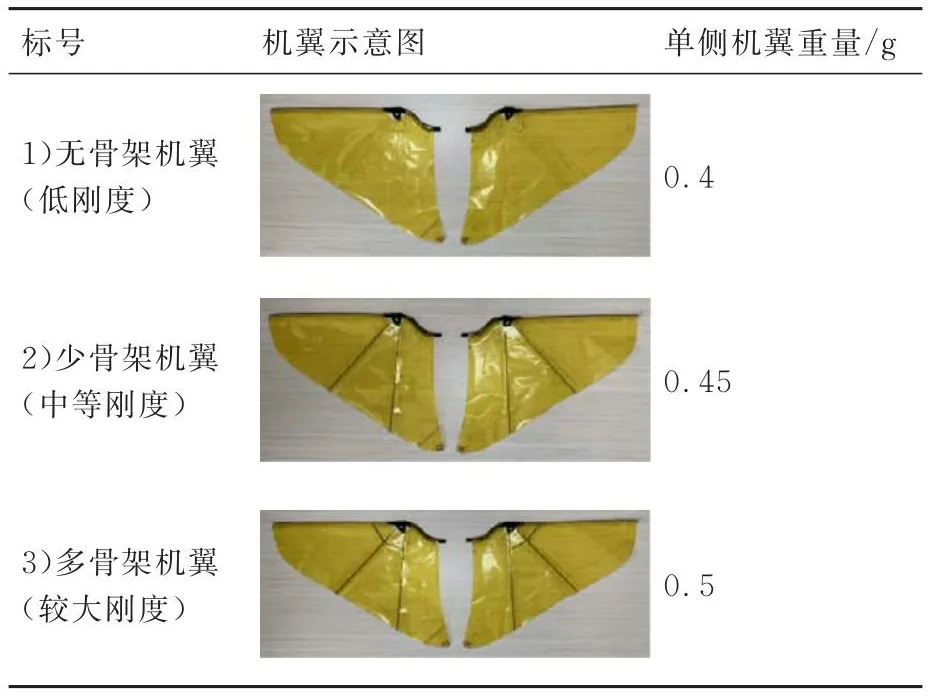
表2 机翼结构示意图Table 2 Schematic diagram of wing structure

图7 小型仿鸟扑翼飞行器试验样机Fig.7 Experimental prototype of small bird-scale flapping-wing vehicles

2.2 测试系统

静态和动态气动力测试平台如图8和图9所示。高速摄像机（i-SPEED 3）捕捉的速率500 帧/s，三轴力传感器的性能指标如表3所示。通过高速摄像机1和高速摄像机2在线捕捉机翼的瞬态变形角ψs和ψc。以机翼气动中心为特征点，通过i-SPEED Suite便可获得机翼前缘和后缘变形角的幅值和变化规律，用于伪稳态空气动力学模型预测气动力。为减小环境噪声对气动力测试结果的干扰，采用巴特沃斯低通滤波器对采集的力数据进行滤波。

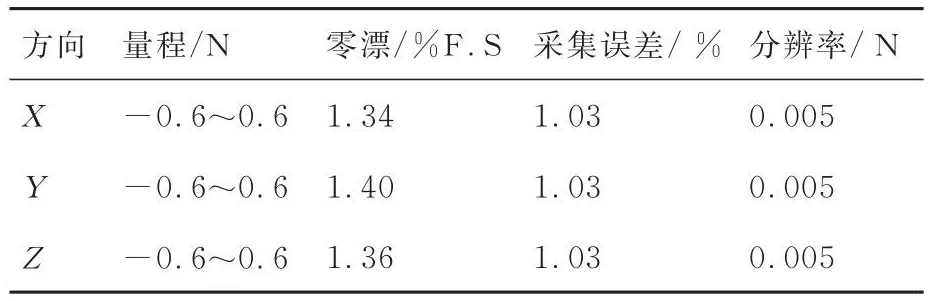
表3 三维力传感器的性能指标Table 3 Performance index of 3D force sensor

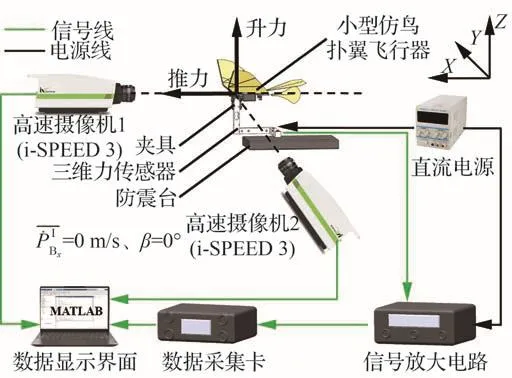
图8 静态气动力测试平台Fig.8 Test platform of static aerodynamic forces

图9 动态气动力测试平台Fig.9 Test platform of dynamic aerodynamic forces

值得注意的是，静态气动力的测试分析可以考虑扑翼机零来流速度起飞时的实际情况，相应的推力特性对提高扑翼机飞行灵活性十分重要。而在动态升力的测试分析中，飞行器主动绕旋转机构的被动转轴旋转，通过调整俯仰角调节机构，可以考虑飞行器在不同俯仰角β下的动态升力。基于高速摄像机3获得的旋转飞行周期Tr，当旋转悬臂长度为Lr时，通过式（13）可计算飞行器的平均前向飞行速度

3 扑翼气动力测试与解析模型修正

3.1 基于传统伪稳态空气动力学模型的气动力分析和预报

基于静态气动力测试平台的数据，使用第1节的气动力学模型定量预测小型仿鸟扑翼飞行器在不同平均拍动频率下的气动力。3种不同刚度机翼实测和预测气动力的比较如图10～图12所示，可看出预测气动力与实测气动力变化的趋势一致。但是在行程开始和结束阶段，实测与预测的瞬态气动力数值及其变化曲率存在一定差异。文献［5，25］研究结果也得到了佐证，这是由扑翼尾迹捕获气动力效应引起。在反转运动时，机翼与前一行程中产生的流体尾迹相互作用。机翼后面的流体由于惯性，倾向于保持其速度。当机翼改变方向时，机翼和流体之间的相对速度大于绝对速度，从而在行程开始和结束阶段会产生更大的力。而伪稳态空气动力学系数只考虑了延迟失速和旋转升力的非定常动力学效应［25］，因此在行程开始和结束阶段所预测的气动力数值和曲率存在误差。除此之外，由于弦向刚度较小，机翼后缘会高阶共振而降低后缘涡的强度，实测瞬态推力在行程中位面处的峰值不尽相同。这种现象在无骨架机翼的拍动行程中尤为明显，而解析计算模型很难考虑扑翼后缘的异常波动现象［22］。通过定量分析图10～图12的气动力数据，实测与预测的瞬态升力峰值的误差均在-21.60%～0.87%，瞬态推力峰值的误差均在-27.62%～-0.57%。

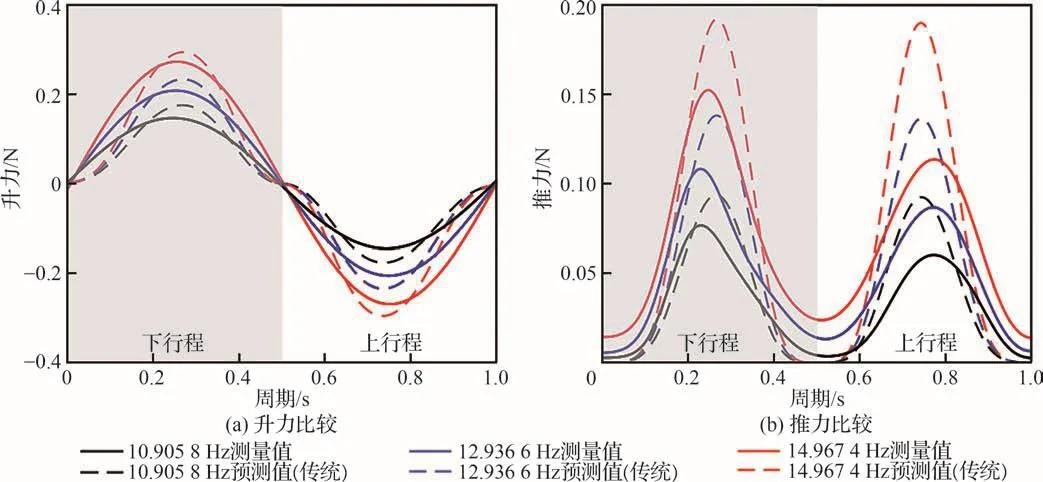
图10 无骨架机翼的实测气动力和预测气动力比较（T =）Fig.10 Comparison of measured aerodynamic force and predicted aerodynamic force of frameless wings （T =）

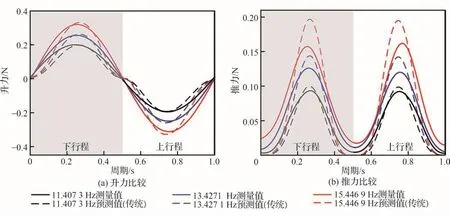
图11 少骨架机翼的实测气动力和预测气动力比较（T =）Fig.11 Comparison of measured aerodynamic force and predicted aerodynamic force of less-frame wings （T =）

图12 多骨架机翼的实测气动力和预测气动力比较（T=）Fig.12 Comparison of measured aerodynamic force and predicted aerodynamic force of multi-frame wings （T=）

为直观反映静态气动力与机翼刚度之间的

关系，定量预测试验样机在不同平均拍动频率下的平均气动力，结果如图13所示。与实际测得的平均升力相比，可明显看到预测的平均升力也几乎为0 N［1，5，17］。这符合静态测试中，飞行器的俯仰角为0°、平均前向飞行速度为0 m/s时，翅膀在上下冲程运动中产生升力相互抵消的实际情况。其次，与图14所示变形角的变化呈现相反的规律，多骨架机翼的平均推力大于少骨架机翼，而无骨架机翼的数值最小。根据第1节的理论分析发现气动力会受到展向和弦向变形的共同影响。多骨架机翼因为具有较小的展向变形和较稳定的弦向变形，使得机翼的结构变形能更稳定地向后缘方向偏转，从而释放出强大而且稳定的后缘涡，进而产生较大的推力［5，11，15，18-19］。随着平均拍动频率的增大，尽管预测的平均推力也随之增大，但是相应的误差却在-10.42%～22.87%。因此，基于1.2节介绍的各向同性气动力系数，只能定性预测扑翼机的气动力，对开展样机改进和优化，利用价值有限。

图13 测量和预测的平均气动力比较Fig.13 Comparison of measured and predicted data of average aerodynamic forces

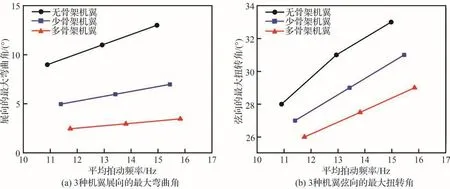
图14 3种机翼的变形角Fig.14 Deformation angles of three wings

3.2 伪稳态空气动力学模型的修正和气动力预报

为提高气动力解析计算模型的预测精度，需要对模型修正。由以往的研究工作［12-13］可知，扑翼气动力系数通常取决于相应的结构形状和流体雷诺数。对于小型低速双平板翼扑翼飞行器，各向同性气动力学系数取值方式表现出了明显的局限性。由于所研究机翼的迎角较大，由机翼表面摩擦引起的切向力分量只能起到很小的作用［25］，在保证运动学参数相同的情况下，基于图13和图14的测试数据，对式（14）所示的法向气动力系数(ϕ（)i=x，y，z）修正。而机翼表面的实际法向力主要来源于zW方向的法向气动力分量，因此本文仅对相应的气动力系数(ϕ)修正，并假定其与机翼的弦向刚度kc有关。新的气动力系数表现出各向异性特征，并呈现相同的变化规律，如式（15）所示，确定系数R2＞0.985 3，标准误差RMSE＜0.030 9，可知建立的模型具有较高的准确性和参考性。

通过采用修正后的气动力系数，3种不同刚度薄膜机翼实测与预测气动力的比较结果如图15～图17所示。与传统伪稳态空气动力学模型相比，预测的气动力峰值精度得到了改善：升力峰值的误差从-26.60%～0.87%降到了-9.83%～9.07%；推力峰值的误差从-27.62%～-0.57%降到了-9.05%～5.71%。由图18可以发现，预测的平均升力近似为0 N。相较于传统伪稳态空气动力学模型的预测结果，理论预测的平均推力误差从-10.42%～22.87%降到了-3.37%～7.36%，显示出良好的预测精度。因此，在采用修正后的气动力系数，解析计算模型的精度能够得到有效提升，可以更加准确地预测扑翼产生的静态气动力。

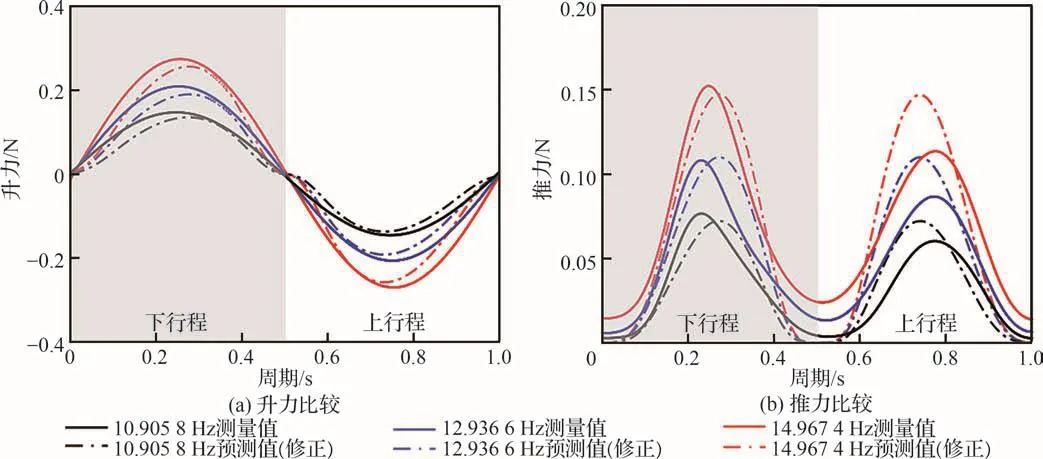
图15 无骨架机翼的实测气动力和预测气动力比较（修正）Fig.15 Comparison of measured aerodynamic force and predicted aerodynamic force of frameless wings （revised）

图16 少骨架机翼的实测气动力和预测气动力比较（修正）Fig.16 Comparison of measured aerodynamic force and predicted aerodynamic force of less-frame wings （revised）

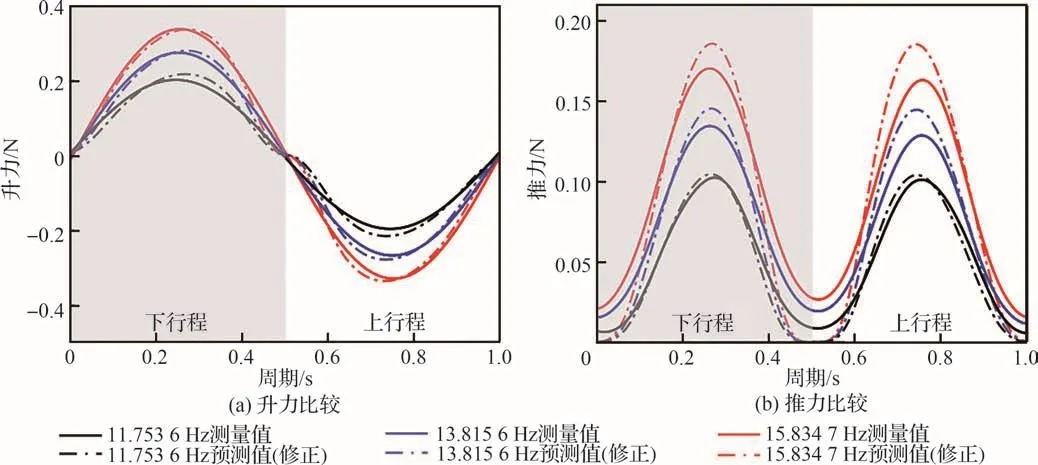
图17 多骨架机翼的实测气动力和预测气动力比较（修正）Fig.17 Comparison of measured aerodynamic force and predicted aerodynamic force of multi-frame wings （revised）

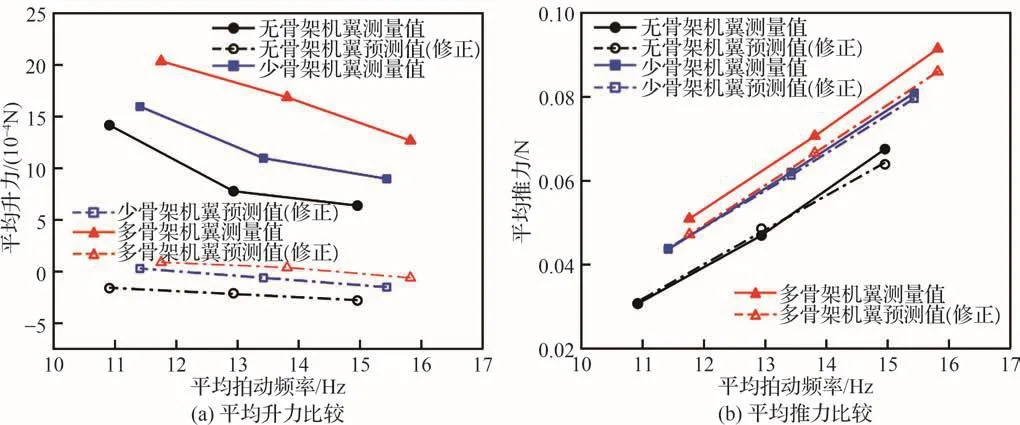
图18 测量和预测的平均气动力比较（修正）Fig.18 Comparison of measured and predicted data of average aerodynamic forces （revised）

为了使修正后的气动力系数更具普适性，如图19所示，通过观察3种不同刚度薄膜机翼的变形角和预测气动力，可以发现与传统伪稳态空气动力学模型的预测规律相同，多骨架薄膜机翼因为具有较小的展向变形和较为稳定的弦向变形，使得相应的推力峰值和平均值最大，少骨架薄膜机翼次之，无骨架薄膜机翼的推力性能最差。并且3种机翼的升力峰值也表现出相同的规律。相应的平均升力因为在上下冲程中相互抵消，与展向变形和弦向变形的关系并不明显。

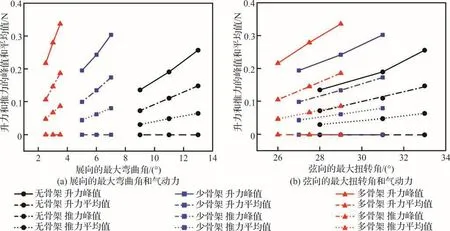
图19 预测的气动力与展向变形和弦向变形的关系Fig.19 Relationship between predicted aerodynamic force and wingspan deformation and chord deformation

4 动态气动升力的测试和预报

根据小型仿鸟扑翼飞行器静态飞行气动力测试和分析预测结果，可以发现虽然无骨架机翼和少骨架机翼的质量较小，但相应比刚度却小于多骨架机翼，这并不符合伪稳态空气动力学中的“运动刚体”对象假设，使得相应的气动性能难以达到实际飞行需求。因此基于图9测试平台，测量了装配多骨架机翼实验样机的升力，并用于验证式（14）～式（15）所示气动力系数的有效性。与传统伪稳态空气动力学模型相比，修正后的解析计算模型所预测的升力更接近测量值，结果如图20～图22所示。当俯仰角分别为5°、10°和15°时，升力峰值的误差均有所减小，分别从-23.38%～-7.48%、-19.75%～-2.55%、-30%～5.38%降到了-13.98%～-8.56%、-13.71%～-0.63%、-13.65%～1.98%。

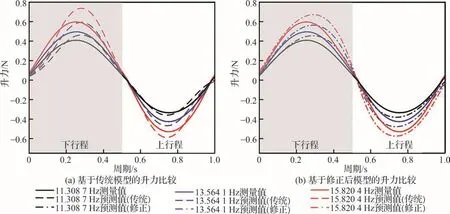
图20 俯仰角为5°时多骨架机翼的实测升力和预测升力的比较Fig.20 Comparison of measured and predicted lift of multi-frame wings at pitch angle of 5°

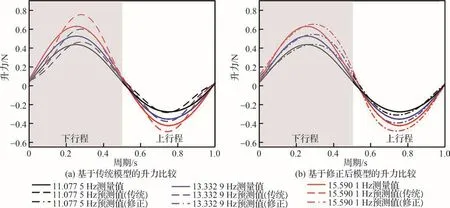
图21 俯仰角为10°时多骨架机翼的实测升力和预测升力的比较Fig.21 Comparison of measured and predicted lift of multi-frame wings at pitch angle of 10°

图22 俯仰角为15°时多骨架机翼的实测升力和预测升力的比较Fig.22 Comparison of measured and predicted lift of multi-frame wings at pitch angle of 15°

图23直观反映动态升力与俯仰角和前向飞行速度之间的关系，定量预测了扑翼机的平均升力。随着俯仰角的增大，前向飞行速度即使在一定范围内减小，机翼产生的平均升力也会增大，说明俯仰角对升力有明显的影响，这也与自然界鸟类的飞行规律相同。与实测平均升力的规律类似，随着平均拍动频率的增加，预测的平均升力也呈现近似线性增长的趋势。但是相较于传统伪稳态空气动力学模型的预测结果，由式（14）～式（15）所预测的平均升力更接近实测平均值：理论预测值与测量值之间的误差从-27.92%～-17.43%降到了-15.61%～-4.82%。因此，基于修正的气动力系数提出的解析计算模型能够较好地预测小型低速双平板翼扑翼飞行器产生的气动力，对开展仿鸟扑翼飞行器的优化设计和加快实验样机改进，有着重要的实际意义。

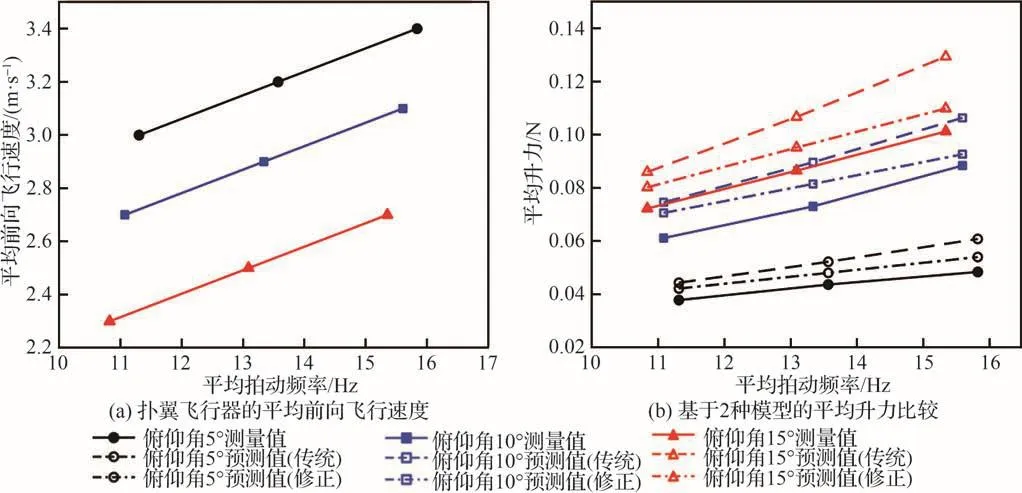
图23 小型仿鸟扑翼飞行器的平均前向飞行速度和平均升力Fig.23 Average forward flight speed and average lift of small bird-scale flapping-wing vehicles

5 结论

1） 基于飞行器机体位置固定条件下的静态扑翼气动力测试结果，对传统伪稳态空气动力学模型的气动力系数修正，表现出各向异性特征，并且修正后的公式具有相同的结构和变化规律。通过对2种模型预测结果进行对比，修正后的气动力预测模型所预测的瞬态气动力峰值和平均值更接近实测气动力：静态升力和静态推力的峰值误差由±22%和±28%均降到±10%，平均推力误差由±23%降到±8%。

2） 基于多骨架机翼动态测试数据，对比了2种模型的动态升力预测精度。测试和分析结果表明，修正后的气动力预测模型精度更高。升力峰值的误差分别从±30%降到±14%；平均升力的误差从±28%降到±16%。因此，改进后的解析计算模型能较好地预测小型低速双平板翼扑翼飞行器产生的气动力，对开展仿鸟扑翼飞行器优化设计和加快实验样机改进有着重要意义。