中等展弦比飞翼布局无人机后缘射流滚转控制

邵帅，郭正，，贾高伟，陈清阳，侯中喜，张来平

1.国防科技大学 空天科学学院，长沙 410073

2.军事科学院 国防科技创新研究院，北京 100071

中等展弦比（3＜A＜4.5，其中A为展弦比）战术级飞翼布局飞行器兼具大展弦比飞翼的高升阻比优势和小展弦比飞翼的高亚声速/跨声速飞行性能优势［1］，近年来备受军事强国青睐。代表性的技术验证机型包括法国的“神经元”，英国的“雷神”，俄罗斯的“猎人”，中国的“攻击-11”，印度的“SWiFT”，美国的“幻影雷”“X-45A”“X-47A”“X-47B”等［2］。但在机动和配平时，传统舵面的偏转将破坏飞翼布局的电磁隐身外形。同时舵面的使用增加了飞行器外模线上的开孔和狭缝，增大了电磁散射截面积［3］。

后缘环量控制作为一种典型的主动流动控制技术，在机翼后缘射出一股切向流动，在柯恩达效应作用下，射流附着于后缘凸曲面（Coanda表面），并夹带周围流动绕Coanda表面偏转。流线偏转使翼型产生气动型弯曲，改变翼型的环量，进而增大或者减小翼型升力。左右机翼后缘差动射流可实现对飞行器的滚转姿态控制，具备取代传统副翼的潜力。与传统舵面相比，除显著提升飞翼布局隐身特性外，环量控制设备还具有体积小、重量轻、可靠性高［4］和气动噪声小［5］等优点，因而受到广泛关注。

20世纪末，曼彻斯特大学研究团队开始将环量控制技术应用于飞行器姿态控制。与英国BAE系统公司联合，该团队自2005年至今试飞了6架使用环量控制技术操纵的无人机［6］。其中以2010年翼身融合布局的DEMON无人机［7］和2019年中等展弦比（47°后掠）飞翼布局的MAGMA无人机［8］的成功试飞影响最为广泛。后者使用超声速环量控制技术和射流推力矢量技术实现了完全无操纵面飞行。国内南京航空航天大学的史志伟教授团队自2014年起成功进行了使用环量控制设备代替传统舵面的常规布局［9］、鸭翼布局［10］和大展弦比（30°后掠）飞翼布局［11-12］无人机的飞行试验。小展弦比飞翼布局ICE与MAGMA同属北约AVT-239项目，安装垂直安定面后，试飞仍因横航向失稳而受挫［13］。展弦比较小的飞翼面临多种横航向失稳问题［14］，同时作为战术级飞翼平台对机动性要求更高，因此亟待开展针对中等展弦比飞翼布局的射流滚转控制研究。

此外前述飞行试验多基于风洞试验结果，相关整机数值模拟研究少见于报道。利物浦大学的Hoholis［15］和Forster［16］利用自研代码数值模拟了低速和高亚声速飞行时环量控制射流对飞翼布局SACCON的控制效果。Forster的研究［16］中滚转和偏航控制力矩以半模气动数据处理得到。国内徐悦与付志杰等［17］通过半模数值模拟确认低速来流中环量控制能够达到舵面偏转30°产生的俯仰力矩，射流入口为质量流量入口边界。射流控制飞行器的数值模拟涉及高压气室内流、飞翼布局绕流和射流与绕流的相互作用等。进行内外流耦合模拟是准确预测射流控制整机气动特性的基础。

本文首先在团队设计的中等展弦比飞翼平台上利用环量控制激励器（Circulation Control Effector， CCE）代替部分传统副翼，得到后缘射流滚转控制飞翼布局验证机。接着构建内外流耦合的整机数值模拟方案，模拟整机绕流并预测气动特性。最后在数值模拟研究的基础上，开展该型验证机的飞行试验，分析CCE对中等展弦比飞翼布局无人机的滚转控制效果。期望为射流主动流动控制无操纵面飞行器设计构建数值模拟研究基础并提供飞行试验数据参考。

1 计算方法

计算使用非结构混合网格计算流体力学仿真软件HyperFLOW。其求解器基于应用广泛的单元中心二阶精度有限体积方法，能够求解耦合多种湍流模型的三维可压缩RANS方程。在非结构混合网格上的高雷诺数亚/跨声速复杂流场数值模拟中，软件展现出良好的精度和网格收敛性［18-19］。计算中，无黏通量离散使用Roe格式、GG-Cell梯度重构，黏性项使用法向导数法离散，湍流模型采用k-ωSST两方程模型，使用LUSGS隐式格式进行时间步推进。下面将使用飞翼布局绕流算例和椭圆环量控制翼绕流算例对HyperFLOW开展验证工作。

本文使用的中等展弦比飞翼平台由MULDICON布局［20］改进而来，故这里用其验证HyperFLOW求解器对飞翼绕流问题的模拟精度。验证算例来流工况：马赫数Ma=0.4，雷诺数Re=5.6×107，攻角α=0°。计算网格为非结构混合网格，附面层为40层棱柱网格，外部空间由四面体网格填充，机身周围区域进行适当加密。图1展示了中等密度网格细节，3套网格的参数列在表1中。第1层网格厚度小于5×10-6m时，能够保证y+≈1。

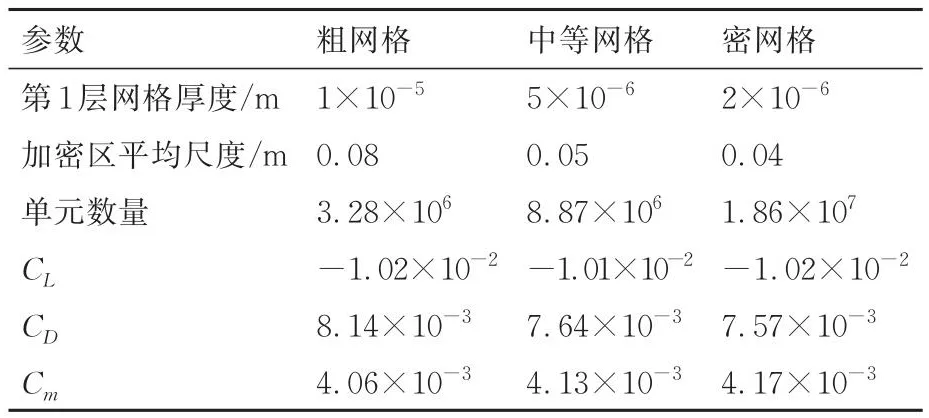
表1 网格无关性研究中网格参数和气动载荷Table 1 Details of grids for refinement study and aerodynamic loads

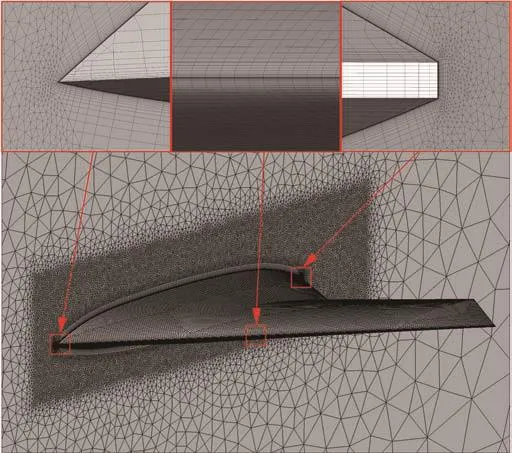
图1 MULDICON布局网格剖分Fig.1 Grid of MULDICON

表1展示了网格无关性验证结果，从中等密度网格到密网格，升力系数CL、阻力系数CD和俯仰力矩系数Cm的变化微小，故选择中等密度网格开展后续研究。图2对比了HyperFLOW与德国宇航中心（DLR）Tau求解器对MULDICON布局的气动特性预测结果，CL、CD和Cm结果均吻合良好，因此本文计算方法可以用于飞翼布局气动特性评估。

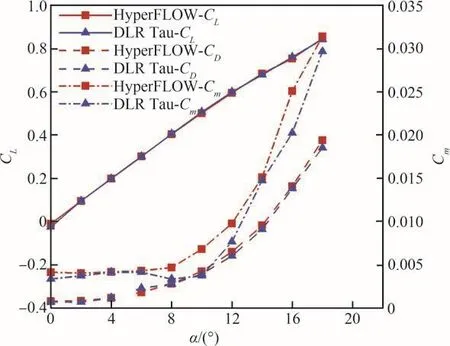
图2 MULDICON布局气动特性Fig.2 Aerodynamic characteristics of MULDICON

6%厚度椭圆环量控制翼绕流［21］是环量控制翼研究的标准验证算例之一。本文验证的来流条件为Ma=0.3，Re=1×106，α=3°。翼型剖面和风洞模型如图3所示，模型展长为弦长的2倍，更详细的模型几何信息请参考文献［21］，机翼表面和气室内部的结构网格参考文献［22］的剖分方式。机翼表面和柯恩达表面法向第1层网格厚度分别为1×10-5c和5×10-6c，以保证y+≈1。

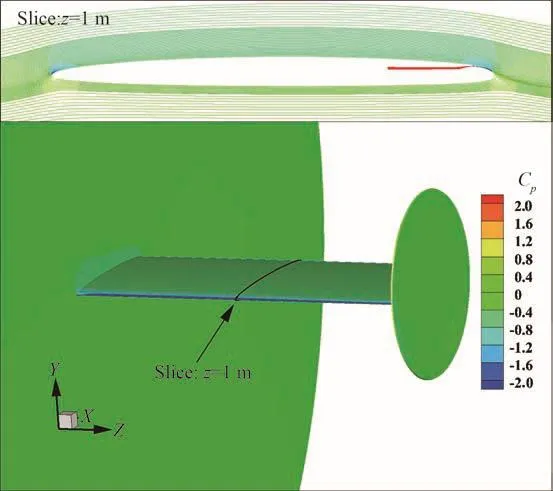
图3 椭圆环量控制翼绕流流场Fig.3 Flow field over elliptical circulation control airfoil

环量控制翼的高压气室前壁面使用压力入口边界条件，总压p0，plenum通过压比NPR=p0，plenum/p∞设置，总温T0，plenum=T∞，p∞和T∞分别为来流压强和温度，速度方向与边界面垂直。射流动量系数Cμ是环量控制的重要无量纲参数，表征射流动量与来流动压的相对大小，定义为

式中：下标b代表边界值；pc为射流动量修正的压力值。

图3展示了椭圆环量控制翼的压力系数Cp云图和展向中间截面z=1的流线图，流线用Cp着色。从截面流线可以看出，射流作用下绕流偏转显著，翼型产生气动型弯曲。图4为展向中间截面升力系数增量ΔCL计算值与试验值（Exp）［21］的对比。计算值与试验值吻合良好，因此本文的计算方法能够满足环量控制翼绕流的数值模拟需求。

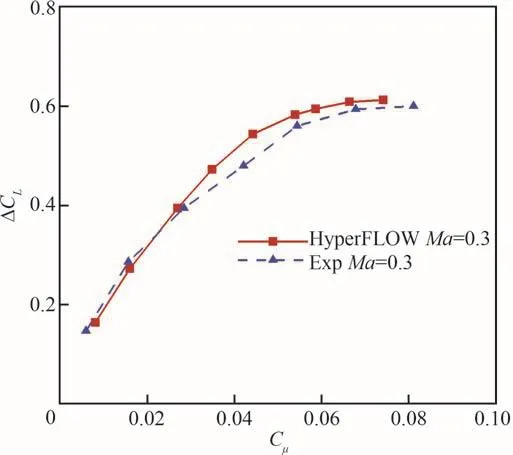
图4 展向中间截面增升效果Fig.4 Lift augmentation of midspan wing section

式中：γ为比热比；R为理想气体常数。为与风洞试验的Cμ计算方法保持一致，数值模拟中对射流出口积分得到ṁ。

压力入口边界上射流动量和压力将产生额外反作用力和力矩。在求解器后处理模块中，将射流动量等效为压力，并将气室内壁和压力入口边界视为常规壁面积分压力和黏性切应力得到整机气动力和力矩。对压力入口边界的压力修正为

2 研究对象

飞翼试验平台基于MULDICON平面形状改进而来，如图5（a）所示，具有53°前缘后掠角，翼展为b=1.5 m，参考面积为Sref=0.718 m2，展弦比为A=3.1。 整机气动力和力矩的参考长度为cref=0.587 m。力矩参考点为重心xcg，距离机身前缘点0.565 m。翼梢截面扭转7°以延迟翼尖失速。飞行试验为开环试飞，故在尾喷口两侧布置小尺寸垂尾以增强航向稳定性。外翼段后缘内侧和外侧分别布置有升降舵和副翼，环量控制激励器取代外侧1/2副翼，宽度为85 mm，后缘的几何尺寸如图5（a）所示。本文以向右滚转为例验证激励器的控制能力，故使用密封胶封闭左侧下出口和右侧上出口以实现差动射流。激励器由离心风机通过软管供气，风机安装位置的选择同时考虑机身内部空间限制和整机纵向稳定性。图5（b）中使用白色棉线指示射流轨迹，离心风机开启后，切向射流绕Coanda后缘偏转显著。

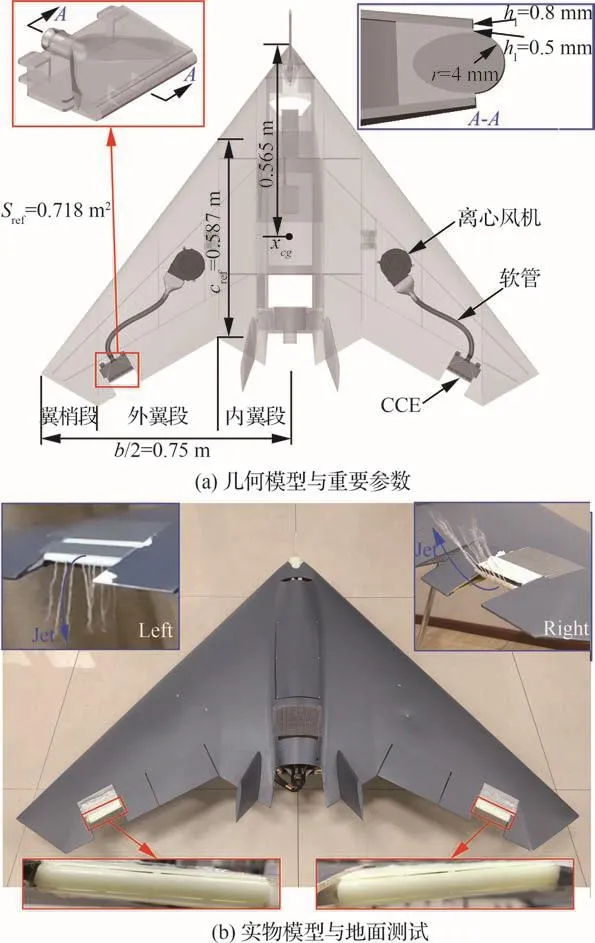
图5 射流控制飞翼布局验证机平台Fig.5 Demonstrator for flight control using jet

离心风机调速为PWM模式，控制信号的频率为500 Hz。定义1个周期内高电平持续时间为控制信号PWM数值（单位为ms）。改变PWM数值控制风机转速，进而实现对射流强度的调控。PWM=0.995 ms时，风机转速为0 m/s。PWM数值越大，风机转速越快，射流出口速度uj越大。利用热线风速仪测量CCE射流出口速度，为后续数值模拟研究提供参考，如图6所示。测量结果如表2所示，射流出口速度随控制信号呈近似线性关系（不含PWM=0.995 ms时uj=0 m/s的数据点，风机在低功率低转速下工作特性不满足线性关系）。通过最小二乘法拟合得到uj=200.5 PWM-225.45(1.19≤PWM≤1.48 ms)，拟合优度R2=0.995 5。

表2 CCE射流出口速度uj随离心风机PWM值的变化Table 2 Jet velocity uj of CCE vs PWM value of centrifugal fan control signal

图6 热线风速仪测量射流出口速度Fig.6 Measurement of jet velocity using hot-wire anemometer

3 数值模拟

本节对验证机整机绕流进行数值模拟以确定环量控制激励器的滚转控制能力。数值模拟使用的非结构混合网格如图7所示。远场边界距离机身表面100倍参考长度，压力入口边界设置在CCE入口截面。外流场非结构网格使用经过验证的MULDICON中等密度网格。不考虑大迎角飞行的情况，故附面层网格之外不再进行加密以减少计算量。CCE内部为结构化网格，射流出口长度和宽度方向分别布置71和51个节点，Coanda表面周向布置121个节点。使用传统舵面控制的验证机飞行速度约为Ma=0.1，故数值模拟算例的来流条件设置为Ma=0.1，Re=1.37×106，α=0°。机身表面和Coanda表面第1层网格厚度分别设为1×10-5和5×10-6m，保证y+≈1。网格总量为944万。

图7 验证机网格剖分Fig.7 Grid of demonstrator

为探究射流产生的控制力矩随射流强度的变化趋势，数值模拟中调整NPR数值令射流出口速度与表2中热线风速仪的测量值相等，并计算射流动量系数，相关数据列在表3中。

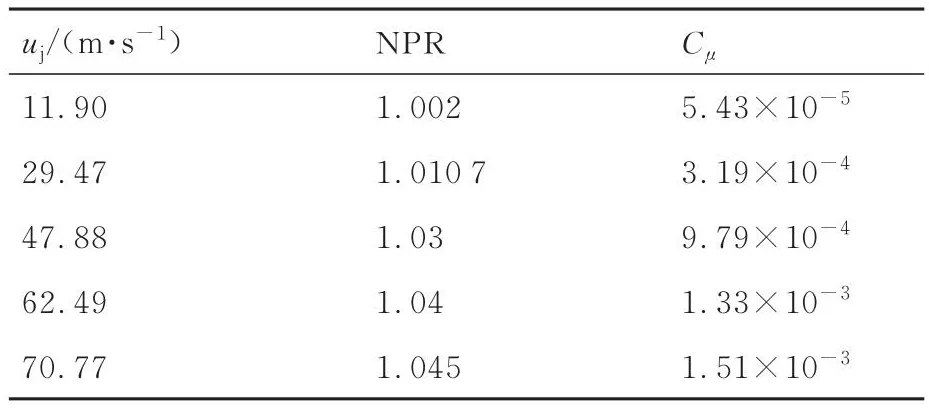
表3 射流出口速度uj对应的压比NPR和动量系数CμTable 3 NPR and Cμ at specific jet velocities uj

图8和图9分别展示了PWM=1.442 ms时，验证机表面压力分布和后缘CCE附近绕流流场，此时uj=62.49 m/s，NPR=1.04，Cμ=1.33×10-3。如图8所示，射流对机翼表面压力场的重构集中于后缘附近区域。射流对同侧机翼表面流动的剪切夹带作用使得压力显著降低，射流脱离曲面后对对侧机翼表面流动的阻滞作用使得压力升高。从z=0.5，-0.5 m截面的表面压力分布可以看出，射流增大了左侧机翼后缘局部升力，并让右侧机翼后缘产生了局部负升力。图9中后缘CCE附近的流场更直观地展示了射流对绕流的夹带作用差异。图中蓝色和红色线分别为绕流流线和射流流线。尽管CCE内部流动出现了大范围的流动分离，但出口处流动仍较为均匀。射流成功夹带绕流发生偏转，但来流的存在减弱了射流对Coanda曲面的附着能力，射流并未如图5中无来流工况下偏转显著。

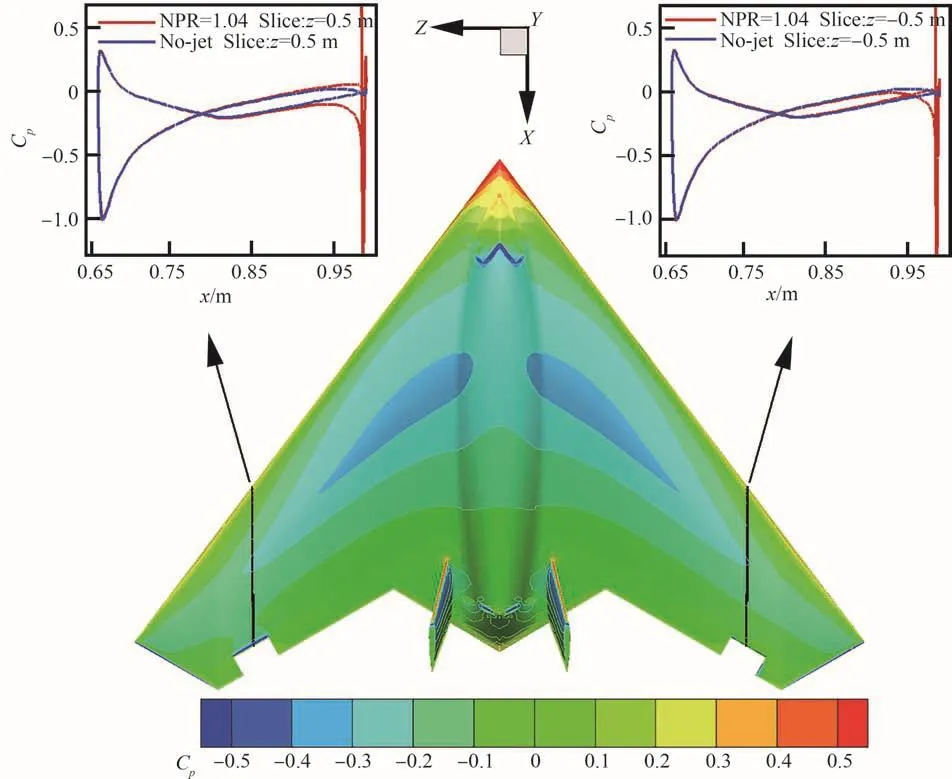
图8 验证机表面压力分布（NPR=1.04）Fig.8 Pressure distribution of demonstrator at NPR=1.04

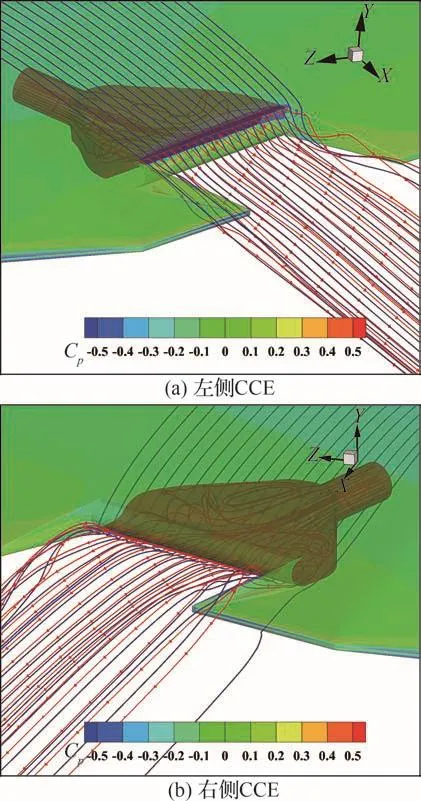
图9 CCE内外流场（NPR=1.04）Fig.9 Flow fields inside and outside of CCE at NPR=1.04

图10展示了滚转、偏航和俯仰力矩系数增量（ΔCl、ΔCn、ΔCm）随射流动量系数Cμ的变化情况。如图10（a）所示，ΔCl随Cμ近似线性增长，即环量控制产生了显著的滚转控制力矩。通过最小二乘法拟合得到ΔCl=3.158 5Cμ，拟合优度R2=0.997 4。根据环量控制中射流对Coanda表面的贴附程度以及增升效率ΔCL/ΔCμ，可将控制分为分离控制阶段和超环量控制阶段［23］。在本文研究的Cμ范围内，射流未完全附着于Coanda表面，且控制效率ΔCl/ΔCμ未发生显著变化，可认为仍处于分离控制阶段。若进一步提高射流强度进入超环量控制阶段，有望获得更强的滚转控制能力。图10（b）展示出射流滚转控制产生的耦合力矩较弱，具体来看，耦合力矩系数绝对值的最大值小于3.2×10-4。

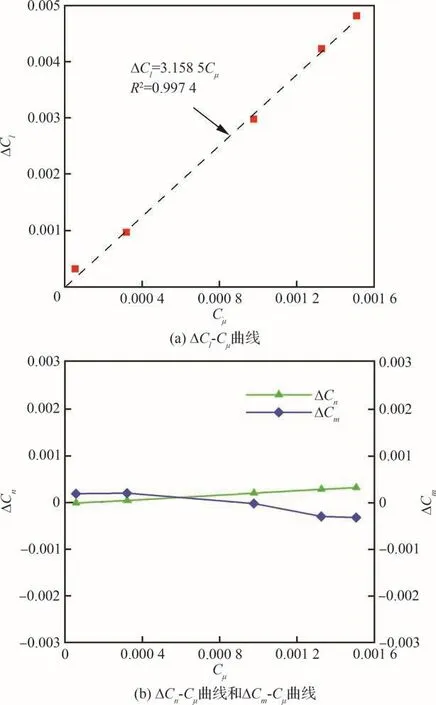
图10 射流产生的控制力矩随射流动量系数的变化曲线Fig.10 Control moments produced by jets vs jet momentum coefficients

4 飞行试验

在数值模拟研究的基础上，开展验证机的试飞工作以验证环量控制激励器的实际滚转控制效果。验证机总重5.65 kg，由90 mm电动涵道提供动力，其最大静推力为3.6 kg。

飞行中由机载自驾仪解析地面遥控信号并向离心风机输出控制信号，以开启射流控制。同时验证机的滚转角等飞行数据由自驾仪记录，着陆后读取并处理相关数据。试验流程分为3个步骤：① 1架次稳定平飞测试，手动配平无人机；② 正式射流控制飞行试验，无人机起飞后进入直线平飞状态，松开副翼操纵杆后，开启射流控制（PWM=1.442 ms），待1～2 s后，副翼介入重新控制无人机；③ 以不同航向进入直线平飞状态重复步骤②3次后降落，以排除滚转控制受当天风场作用的可能性。实际飞行速度范围为30～35 m/s。为统一表示射流和副翼控制信号，本文中将副翼控制信号（PWM=1～2 ms）映射为-1～1的无量纲控制信号，并将射流控制信号（PWM=0.995～1.995 ms）映射为0～1（仅向右滚转）的无量纲控制信号。稳定平飞测试的数据如图11所示。2次稳定平飞段中副翼控制信号维持在中立点附近，滚转角速率在零附近浮动，滚转角无大幅变化，可认为无人机在横航向已经达到配平状态。

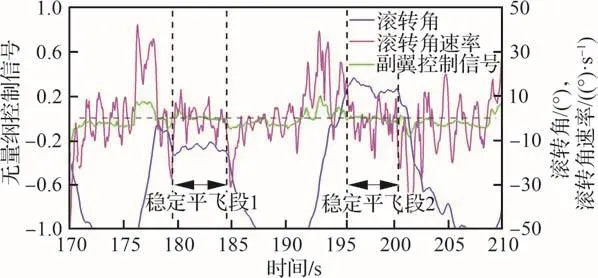
图11 稳定平飞测试数据Fig.11 Data of steady level flight test

图12展示了射流控制飞行试验的画面。在地面视角中，放开副翼操纵杆并且开启射流后，机身显著右滚，滚转角甚至超过80°。在机上视角中，贴附在右侧机翼后缘下表面的白色棉线受到射流作用向上飘动，表明机翼下表面绕流在射流的夹带作用下向上偏转。

图12 射流控制验证机试飞Fig.12 Flight test of demonstrator

试飞过程GPS航迹如图13所示，图中用彩色曲线指示出射流控制时间窗口对应的航迹，3次射流控制按照时间顺序用Jet-1～Jet-3表示。分析3次射流控制前后的航迹变化可以看出：① 射流控制开始前，无人机已经按计划进入直线平飞状态；② 射流控制过程中，无人机开始向右转弯；③ 射流控制结束后，无人机仍保持右转状态并持续一段时间。射流进行向右滚转控制时，无人机向右转弯，与预测航迹变化一致。并且Jet-1与Jet-2和Jet-3的飞行方向几乎完全相反，故可排除完全由低空风场导致无人机滚转状态变化的可能性。

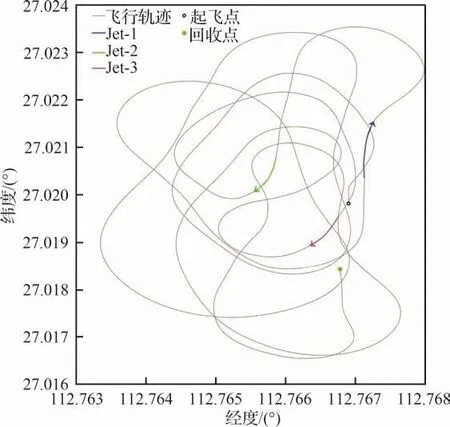
图13 GPS航迹Fig.13 GPS movement track

图14展示了滚转控制信号与横航向状态参数的时间历程曲线。如图14（a）所示，3次射流控制均为阶跃控制信号，PWM=1.442 ms。Jet-2射流的开启操作存在一定迟滞。在射流时间窗口内，副翼控制信号稳定在中立点附近，以排除副翼偏转对滚转状态的影响。在后缘射流的作用下，无人机的滚转角从0°增加到60°甚至超过80°。图14（b）给出了滚转和偏航角速率的时间历程曲线。3次射流中，滚转角速率均保持在20 （°）/s以上。同时滚转控制产生了附加偏航作用，但平均偏航角速率小于10（°）/s。

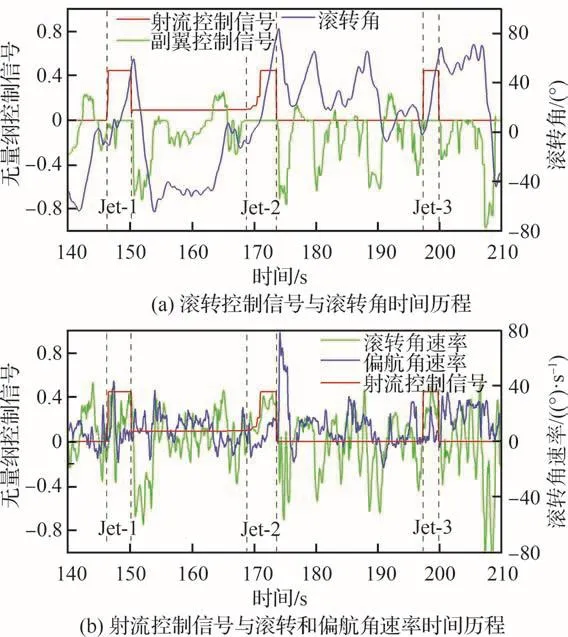
图14 滚转控制信号与横航向状态参数时间历程Fig.14 History of roll control signal and lateral status parameters

为进一步量化分析射流滚转控制效果，定义滚转状态典型参数如图15所示。射流作用时副翼控制信号仍存在轻微抖动。故选择射流开启并且副翼控制信号完全中立的时间窗口计算平均滚转角速率。由于迟滞作用，射流信号结束后滚转角继续增大到峰值后回落，定义该值为射流控制得到的最大滚转角。量化射流滚转控制效果的典型参数列在表4中。射流控制得到的最大滚转角和滚转角速率分别达到83.9°和40.1 （°）/s。在定义的时间窗口内，3次射流的平均滚转角速率范围为25.5～26.7 （°）/s，数据具有显著的一致性。Jet-2与Jet-3数值偏差极小（0.02 （°）/s），与Jet-1偏差稍大为1.2 （°）/s。可能的原因是，如图13所示，第1次与后2次射流测试时无人机航向相反，风场对反向飞行的无人机贡献了相反的滚转作用。

表4 射流控制滚转状态典型参数数值Table 4 Values of typical parameters indicating effectiveness of roll control using jet

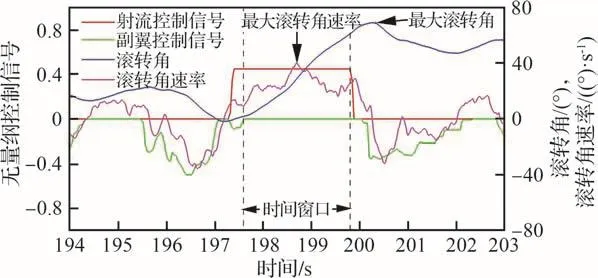
图15 射流控制滚转状态典型参数示意图（Jet-2）Fig.15 Schematic for typical parameters indicating effectiveness of roll control using jet （Jet-2）

表5列出了文献［9，12，24］中3款射流控制无人机的最大滚转角速率。其中，Ref-1和Ref-2的平台是大展弦比平直翼布局无人机，Ref-3的平台是大展弦比飞翼布局无人机，射流滚转控制激励器均布置在机翼外段。本文的激励器在中等展弦比飞翼平台上实现的最大滚转角速率显著大于Ref-1和Ref-2的结果［9，24］，在数值上更接近于Ref-3的结果［12］。但Ref-3中单侧滚转控制激励器宽度占半展长的30%。本文中激励器仅取代了副翼的一半（宽度为半展长的11.3%），若能替换整个副翼，预计将能获得更强的滚转控制效果。最后，考虑到激励器在后缘上的展向长度和具体位置不同，以及无人机平台的滚转阻尼不同，表5中不同无人机的最大滚转角速率数值仅作为参考。

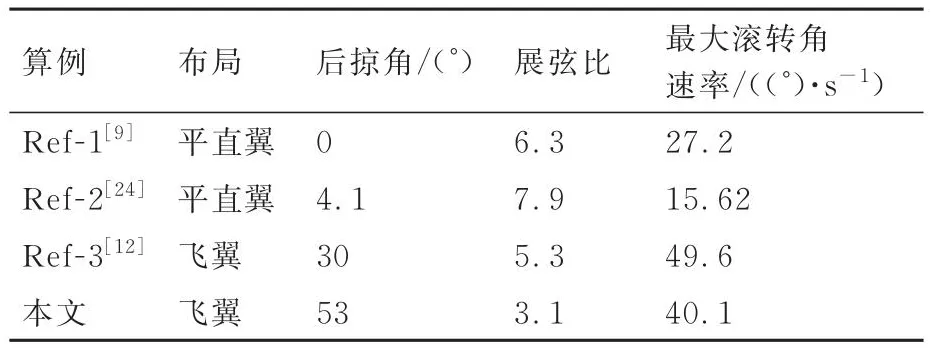
表5 不同无人机射流滚转控制效果Table 5 Effectiveness of jet roll control effector on different UAVs

5 结论

利用环量控制激励器代替中等展弦比飞翼布局无人机的外侧1/2副翼，构建数值模拟方法研究射流控制飞翼布局无人机的气动特性，并且开展飞行试验探究环量控制射流对中等展弦比飞翼布局无人机的滚转控制能力。得到以下结论：

1） 射流控制飞行器整机数值模拟方案使用压力入口边界条件，并考虑射流动量对气动力的贡献，可实现对飞翼绕流和激励器内流的耦合模拟并预测整机气动特性。

2） 数值模拟研究表明，在所研究的射流动量系数范围内，滚转控制力矩系数随射流动量系数近似线性增长，同时未产生显著的横航向或横纵向耦合力矩。

3） 后缘环量控制射流对中等展弦比飞翼布局无人机实现了有效滚转控制，平均滚转角速率达到25.5～26.7 （°）/s，最大滚转角速率达到40.1 （°）/s，最大滚转角为83.9°。

致 谢

感谢中国空气动力研究与发展中心的李永红博士和利物浦大学的Matthew J.FORSTER博士，提供椭圆环量控制翼几何模型用于本文的数值方法验证。