初始应力状态对薄壁件双侧滚压影响规律
路来骁,徐长官,刘建华,秦美镇,吕英波,阎玉芹
山东建筑大学 机电工程学院,济南 250101
随着现代飞机整体化设计水平的不断加强,航空结构件向着大型化、复杂化、轻量化纵深发展,大大提升了飞机的整体性能。目前飞机的隔框、梁、起落架、肋板、油箱等结构件主要通过铝合金预拉伸板材进行铣削制造,然而铝合金板材在切削加工过程中极易受毛坯应力、加工应力、切削力、切削热等因素的影响,导致不同程度的加工变形问题,如弯曲、扭曲、弯扭组合变形等,结构件的加工尺寸精度不能达到设计要求。
针对航空结构件的变形预测与控制问题,国内外学者进行了大量研究。郑耀辉等[1]研究表明毛坯中的初始残余应力是整体构件变形的主要因素,另在机加工过程中引入表面残余应力的作用下结构件将发生二次变形。Masoudi等[2]研究了在不同的加工状态下机械载荷和热载荷对7075-T6铝合金薄壁件残余应力和变形的影响。Gao等[3]通过构建薄壁零件加工变形的半解析预测有限元模型获得了毛坯残余应力对加工变形的影响规律。廖凯等[4]通过测量工件初始应力和加工应力的分布情况,基于弹性力学理论和数学解析方法建立了结构件应力-变形预测数学模型。Fan等[5]研究了材料内部初始残余应力引起的弹性能演变对零件加工变形的影响。Wang等[6]基于能量法综合考虑毛坯应力和加工应力的影响,建立了预测多隔框零件加工变形的模型。Li等[7]基于灵敏度分析法提出了一种用于评估初始残余应力和表面残余应力对加工变形不确定性影响的方法。Weber等[8]通过不同的加工模式研究了加工应力对铝合金整体结构件的影响。Cerutti等[9-10]通过构建只含有初始残余应力场的有限元模型预测工件加工过程中初始残余应力引起的加工变形,进而分析了工件初始残余应力状态、夹具布局及加工顺序对加工质量的影响。
然而因航空结构件结构千变万化、材料的初始状态不稳定等因素影响,结构件变形问题一直得不到较好的解决。因此对于变形超差的零件必须进行后处理,如变形校正[11]。目前对航空结构件的校正方法主要有反弯校正[12]和滚压校正[13],滚压校正又因其高安全性的特点在航空航天领域广泛使用。笔者课题组对滚压校正工艺进行了基础性研究,基于能量原理提出了航空结构件滚压校正载荷的预测方法[14]。
作为一种表面处理技术,滚压是通过光滑高硬度的滚轮碾压工件表面,工件表层材料发生塑性变形并产生残余压应力。杨东[15]、李宁[16]等分别对钛合金Ti-6Al-4V和纯铁表面进行低塑性滚压处理,发现滚压工艺使材料表面形成更深的强化层,表面显微硬度提高,降低了应力集中。为研究滚压对塑性变形及应力场的影响,许多学者采用有限元技术对滚压工艺进行仿真分析。赵吉中等[17]对列车的车轮进行滚压强化仿真模拟,得出滚压次数为3次、滚压力为1 kN的情况下车轮疲劳寿命提高约58%。胡兴远等[18]建立了AISI 4340钢的三维滚压模型,研究了预加载荷和滚压应力场耦合作用对工件表面强化残余应力的影响。Zheng等[19]建立了工件表面的穿透深度模型和表面形貌仿真模型,研究了超声滚压对7075铝合金表面形貌的影响。梁志强等[20]借助ABAQUS仿真软件研究了不同滚压参数对工件表层残余应力的影响。
因此对滚压校正工艺进行有限元分析对于提高校正工艺的质量稳定性具有积极作用。然而现有有限元分析多集中在表层应力场,并未对滚压引起的工件变形及其与滚压应力的耦合关系进行研究。研究者在对滚压校正进行仿真时多采用无初始应力模型,忽略了初始应力和加工应力的影响。值得注意的是加工应力存在于工件表层,而滚压操作也多作用于工件表层,由此可推断初始应力状态对滚压引入的应力场分布应存在较为显著的影响。
本文借助有限元方法开展初始应力状态对铝合金结构件滚压校正的影响规律研究,以典型航空铝合金T型件为研究对象建立三维滚压有限元模型,分析不同初始应力状态下工件的弯曲变形规律,希望通过对工件的应力场及应变场进行综合讨论揭示初始应力状态对滚压应力场的影响作用。
1 有限元模型建立
1.1 有限元模型设置
因航空整体结构件多为壁板、长梁类零件,其结构特征多由腹板和翼缘或加强筋组成,因此选用与其结构类似的T型件为研究对象建立铝合金T型件滚压模型,如图1所示。T型件几何尺寸为30 mm×30 mm×150 mm,壁厚均为3 mm。滚压校正采用的滚轮半径为14 mm,厚度为8 mm,采用ABAQUS/Explicit软件进行滚压校正仿真分析。

图1 T型件滚压有限元模型Fig.1 Finite element model of T-shaped parts rolling
在实际的滚压过程中,滚轮塑性变形很小,和T型件相比变形相差较大,因此可将滚轮视为刚体,只需设置T型件密度、弹性模量和泊松比即可,设置铝合金7050-T7451材料参数如表1所示。
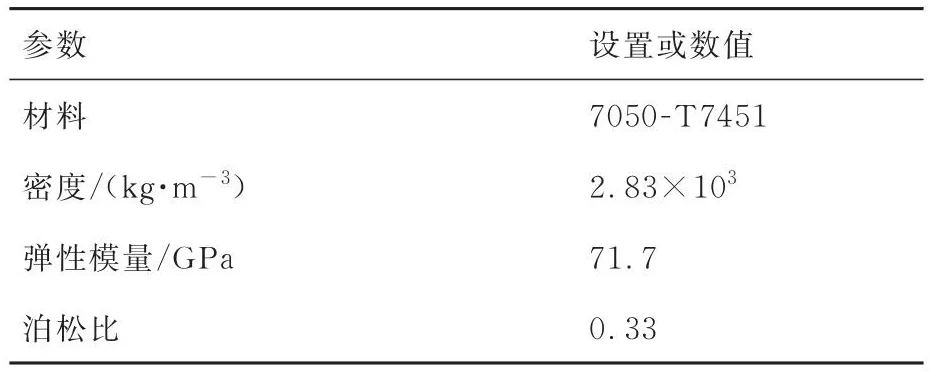
表1 铝合金7050-T7451材料参数Table 1 Aluminum alloy 7050-T7451 material parameters
滚压操作主要对工件浅表层材料产生物理影响,因此获得准确的浅表层材料本构模型是保证仿真精度的关键所在。对铝合金7050-T7451铣削加工表面进行自动球压痕试验测试,获得铝合金加工浅表层材料的本构关系模型为[21]
式中:σt为真实应力;εp为塑性应变。
有限元网格划分的精度直接影响仿真结果的准确性,而网格数量过多则计算机的负荷将增大,因此在滚压区域进行网格细化,在控制网格数量的同时提高关键区域的网格密度,如图1所示。滚压区域的网格尺寸为0.1 mm×0.1 mm×1.0 mm,其余部分为1.5 mm×1.5 mm×2.0 mm,单元类型为C3D8R(八节点六面体线性减缩积分单元)。
在滚压过程中滚轮和工件属于非线性面接触,设置接触时滚轮和工件没有穿透现象,接触类型选用“自动面对面接触”,其中工件是可变形接触体,滚轮是刚性接触体。根据接触的定义原则选择刚体表面为主面,因此将滚轮外表面设置为主面,滚压部件的表面设置为从面。工件和接触面之间有摩擦的相互作用,设置库伦摩擦系数为0.3。
在仿真模拟中根据滚压过程的实际工况设置4个分析步,分别为初始应力状态的施加、滚轮加载、滚轮滚压、滚轮卸载,整个过程在工件底部设置简支梁约束。
1.2 基于裂纹柔度法的毛坯板材残余应力测量
航空结构件加工变形与毛坯板材蕴含的初始应力密不可分[22]。铝合金预拉伸板材在淬火、预拉伸等过程中逐步形成了残余应力场,将该应力统一称为“毛坯应力”,以便同后续机械加工引入的“加工应力”区分。
裂纹柔度法因其优异的敏感性被广泛用于铝合金预拉伸板材毛坯应力的测量[23]。裂纹柔度法的测量原理是在被测工件表面引入一条深度逐渐增加的裂纹释放残余应力,通过测定指定点处随深度变化的应变量计算残余应力[24]。
测量试验选用60 mm厚的铝合金7050-T7451预拉伸板材为试验材料,如图2所示。使用济南科特DK7745型电火花线切割机床引入0.2 mm宽的裂纹,电极丝为∅0.18 mm钼丝。在引入裂纹的背面粘贴BSF120-3AA-T高精度型电阻式应变片采集应变信号,敏感栅的尺寸为3.1 mm×1.0 mm,沿板材厚度方向进行线切割,切割深度为60 mm,切割30次,每次切割2 mm。采用西格玛ASMB2-8型应变采集箱采集应变值,精度为0.1 με。

图2 裂纹柔度法毛坯应力测试试验Fig.2 Test of blank stress by crack flexibility method
根据试验测量的应变值计算获得60 mm厚的铝合金7050-T7451预拉伸板材毛坯应力分布如图3所示,可见板材的毛坯应力整体呈“M”形分布,在轧制方向表面为拉应力,在横向方向表面为压应力,满足力平衡和力矩平衡条件,分布规律与Prime和Hill[25]的研究基本一致,验证了测量试验的准确性。
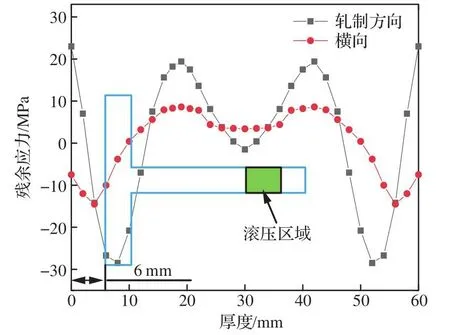
图3 60 mm厚铝合金7050-T7451毛坯应力分布及T型件位置Fig.3 Stress distributions of 60 mm thick aluminum alloy 7050-T7451 blank and position of T-shaped parts
1.3 初始应力状态的施加方法
在结构件加工制造过程中随材料去除,板材内部的应力平衡状态被打破,结构件内部进行应力再分配以达到新的平衡状态,毛坯应力与加工应力平衡将导致结构件发生变形。在有限元模型中因需综合考虑毛坯应力和加工应力,暂不能采用子程序功能进行应力场施加,因此借助ABAQUS软件自带的“预定义场”功能进行初始应力状态的设置与施加。
设定T型件位于距板材表面6 mm深度处,且工件长度方向沿板材轧制方向,如图3所示。将工件沿板材厚度方向分层并分别设置单元集合,并将离散化的毛坯应力数值逐层施加到单元集合,施加毛坯应力后的工件应力云图如图4所示。

图4 T型件初始应力云图Fig.4 Initial stress state of T-shaped parts
根据剥层法测得铝合金7050-T7451加工表面的加工应力数据如图5所示。试验选用硬质合金整体立铣刀,其直径为20 mm、齿数为3、前角为19°、后角为12°、螺旋角为30°。加工工艺参数如下:切削速度为628 m/min、轴向切深为5 mm、径向切深为12 mm、每齿进给速度为0.06 mm。

图5 铝合金7050-T7451加工应力及T型件施加位置Fig.5 Processing stress of aluminum alloy 7050-T7451 and application position of T-shaped parts
由图5可知应力整体分布呈“勺子”状,在距离工件表面25 μm的位置处加工压应力达最大(-136 MPa),随工件表层深度增大加工压应力逐渐减小,在100 μm处逐渐趋于稳定。
为将加工应力施加到有限元模型中,结合滚压表层网格的大小设定加工应力的作用区域为100 μm。因此将加工应力沿工件表层深度方向均匀化,即以平均应力代替实际的加工应力。根据加工应力测量数据计算获得加工应力在两个方向上的大小约为-50 MPa,并将其作为加工应力施加到工件表层区域单元。
2 有限元模型试验验证
因主要研究初始应力状态对滚压校正的影响,故采用滚压区域的应力数值进行模型验证。根据工件实际加工情况,毛坯应力和加工应力同时存在,故验证毛坯应力和加工应力耦合作用下的有限元模型。
毛坯材料选用60 mm厚的7050-T7451铝合金板材,工件在板材上的位置如图3所示。为保证加工应力与1.3节中的设置匹配,加工用刀具和加工参数与之保持一致,获得T型工件。采用自制的双侧滚压设备进行滚压处理,滚轮材料为GCr15,滚轮直径为28 mm,宽度为8 mm,滚轮圆角为1 mm,滚压参数设置为滚压道次1次、滚压力为4 000 N。
采用Proto公司的X射线残余应力分析仪测量滚压处理后工件滚压区域浅表层的残余应力,采用侧倾固定φ法、Cr靶,衍射角为139.3°。为提高验证试验的可靠度,在工件对称轴线与两侧75 mm处选择3个点位进行X方向应力测量,试样测量点及设备如图6所示。每个测量点分别测量3次,取其平均值,对比有限元仿真与试验测得的数据,结果如表2所示,可知有限元仿真数据与试验数据存在一定误差,最大误差为12.87%。分析造成误差的主要原因在于仿真模拟是在理想环境中进行的,而在实际试验中滚压应力的产生受初始应力状态、滚压工艺、测试误差等影响。综上所述,基于上述影响因素,有限元仿真数据与试验数据的差距在误差允许范围内,证明建立的有限元模型准确可行。

表2 仿真与试验的残余应力对比Table 2 Comparison of residual stress obtained by simulation and tests

图6 滚压区域残余应力测量Fig.6 Residual stress measurement in rolling area
3 初始应力状态对工件变形及残余应力的影响
3.1 初始应力状态对滚压变形的影响
工件内部应力状态是造成工件变形的重要因素,在施加初始应力后工件内部的应力自平衡状态被打破,为达到“力平衡”和“力矩平衡”状态,工件整体会发生弯曲变形。提取工件在施加完成初始应力后的变形见表3,表中使用的坐标为整体坐标系,且工件局部坐标系的X轴、Y轴、Z轴与整体坐标系一致,由表3可知滚压前最大变形量分别为0、4.551×10-2、8.756×10-2mm。
2011年10月,在面向全社会公开征求意见的基础上,财政部、科技部联合印发了《关于调整国家科技计划和公益性行业科研专项经费管理办法若干规定的通知》(财教〔2011〕434号,以下简称《通知》),对公益性行业科研项目经费的开支范围、预算编制和结余资金管理、主管部门和项目单位的管理职责进行了调整和进一步的明确。新出台的《通知》有明确的政策导向,将对水利公益性行业科研专项项目的管理产生重大影响。
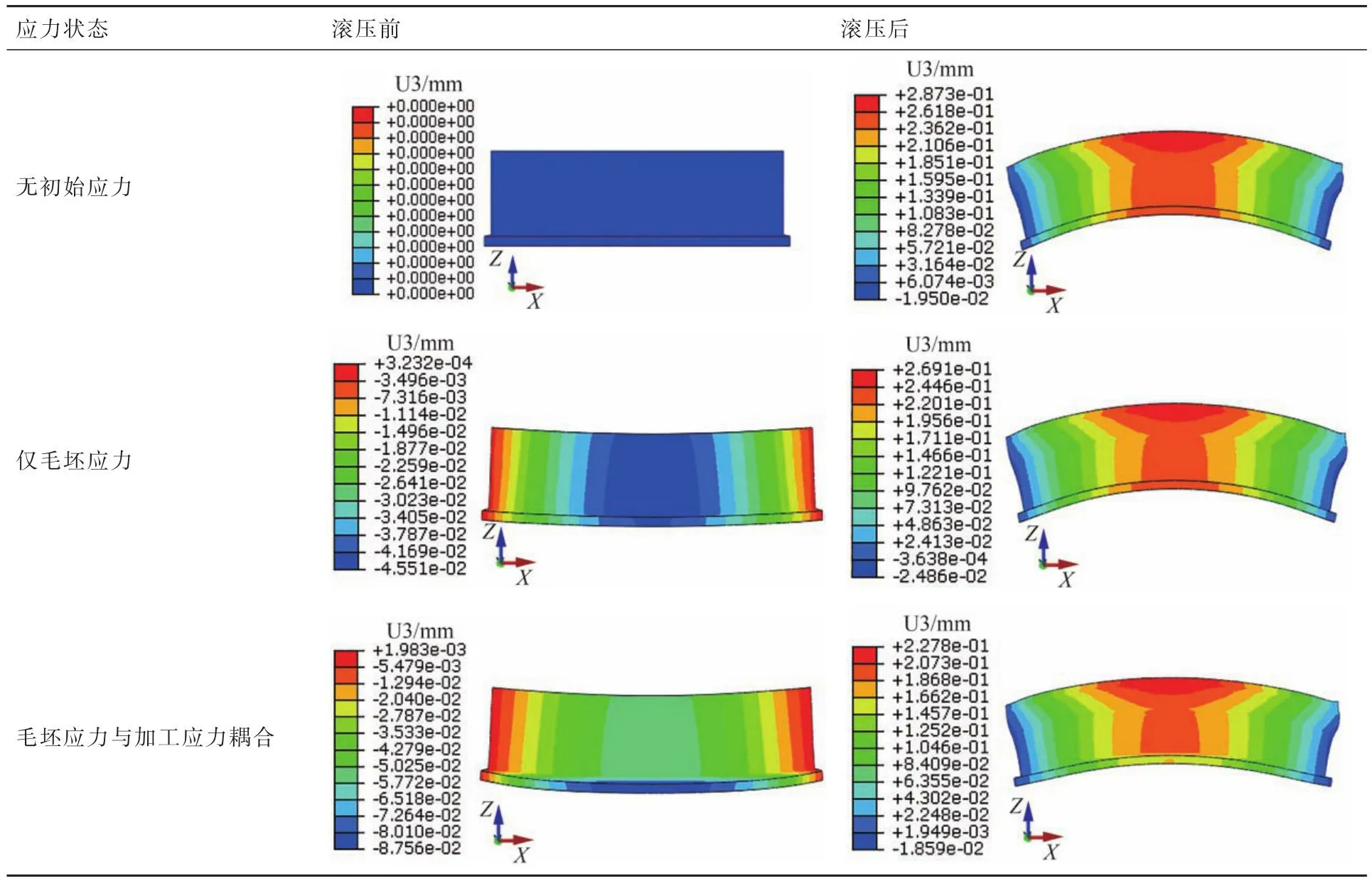
表3 T型件变形云图Table 3 Deformation cloud diagrams of T-shaped parts
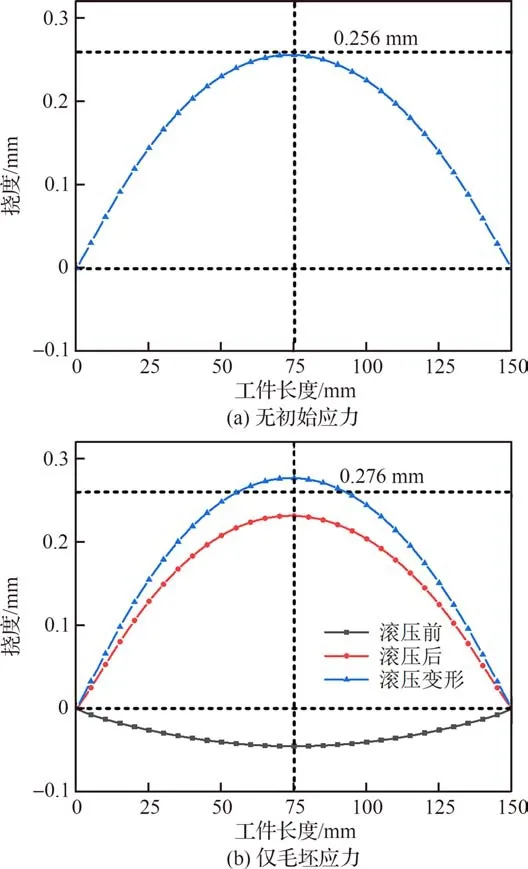
待零件滚轮滚压完成后的变形云图见表3,可见在不同的初始应力状态下零件在滚轮滚压后均呈上凸弯曲变形趋势,且最大变形量均在工件顶部中间位置处,分别为2.873×10-1、2.691×10-1、2.278×10-1mm。为确定中线节点处的位移计算滚压前后的变形差值为滚压变形,结果如图7所示。可见无初始应力、仅毛坯应力、毛坯应力与加工应力耦合3种应力状态下滚压导致的工件变形分别为2.56×10-1、2.76×10-1、2.49×10-1mm。若以无初始应力状态下的滚压变形为基准,则仅毛坯应力状态下滚压变形提高7.8%,毛坯应力与加工应力耦合应力状态下滚压变形降低2.7%。由此可进一步得出在本文仿真条件设定下毛坯应力对滚压变形的影响程度约为7.8%;在仅毛坯应力的影响基础上加工应力的影响约为9.8%,且毛坯应力与加工应力的作用方向相反。由此可知毛坯应力与加工应力导致滚压变形存在较为明显的区别。
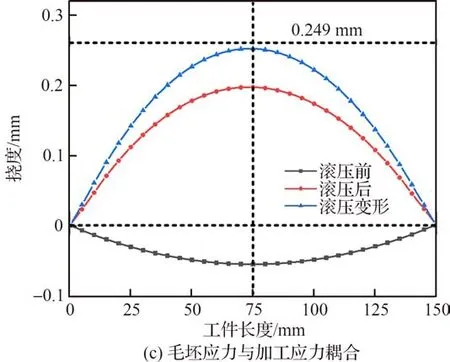
图7 工件滚压变形挠度曲线Fig.7 Workpiece rolling deformation deflection curves
3.2 初始应力状态对滚压残余应力的影响
滚压完成后,除滚压变形外残余应力也是重要的滚压产物。为研究初始应力状态对滚压残余应力的影响,提取毛坯应力与加工应力耦合状态下滚压完成后的应力云图如图8所示,可见滚压完成后,在滚压区域会残留较大幅值的残余应力,Mises应力峰值达334.9 MPa(图8(a))。
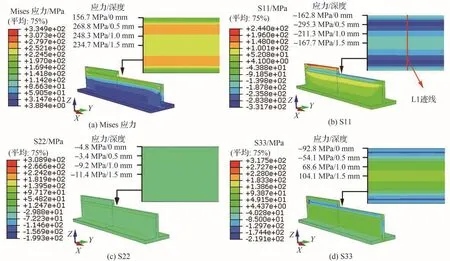
图8 毛坯应力与加工应力耦合状态下的残余应力云图Fig.8 Residual stress cloud diagrams under coupled state of blank stress and machining stress
平行滚压前进方向(X方向,图8(b)S11分量)滚压区域全厚度范围内均存在残余压应力,在其他区域存在残余拉应力。在滚压区域残余应力沿壁厚呈分层分布,应力峰值在次表面;在非滚压区域,X方向应力分量明显随与滚压区域距离增大而减小。值得注意的是在工件顶端区域存在较大幅值的残余拉应力;这是因为滚轮滚压位置距工件顶面存在2 mm的距离,而工件又发生了上凸弯曲变形,导致该部分材料产生较大拉伸变形,故存在较大拉应力,从应力状态分析推断该区域是滚压后工件的薄弱点。
工件沿壁厚方向(Y方向,图8(c)S22分量)整体应力幅值较小,仅在滚压区域外围存在部分应力峰值。这是由于在该方向材料受约束作用较小,材料发生的形变不受周围材料约束,故表现出的应力幅值也较小。在后续分析中该方向的残余应力可暂不考虑。
垂直滚压前进方向(Z方向,图8(d)S33分量)的应力分布与X方向应力分布规律类似,但在滚压区域表面应力为压应力、芯部为拉应力,且非滚压区域的应力幅值差距并不明显。

图9 T型件滚压区域中间截面处的应力分布Fig.9 Stress distributions at middle section of rolling area of T-shaped parts
3种初始应力状态下X方向的滚压残余应力如图9(a)所示,可见应力呈对称分布,随距离表面深度的增大滚压残余应力呈先增大后减小趋势,且在次表面达最大值。在无初始应力状态下表面残余应力幅值为-160.9 MPa,在距离表面0.4 mm处达最大值-294.3 MPa;在仅毛坯应力作用下表面残余应力提高到-168.4 MPa,在距离表面0.4 mm处达最大值-302.9 MPa;在毛坯应力与加工应力耦合状态下,表面残余应力提高为-162.8 MPa,在距离表面0.4 mm处达最大值-296.3 MPa。由此可知X方向应力分量在毛坯应力作用下表面残余应力提高约4.7%,次表面残余应力提高约2.9%;以仅毛坯应力作用下应力状态为基准,在毛坯应力与加工应力耦合作用下表面残余应力降低约3.3%,次表面残余应力降低约2.2%。
3种初始应力状态下Z方向的滚压残余应力如图9(b)所示,可见应力呈对称分布,随距离表面深度增大呈先增大后减小再增大的趋势,残余应力在表面为压应力,在芯部为拉应力。在无初始应力状态下表面压应力幅值为-93.2 MPa,在距离表面0.2 mm深度达最大值-131.2 MPa;在仅毛坯应力作用下表面压应力降低到-78.9 MPa,在距离表面0.2 mm处达到最大值-127.4 MPa;在毛坯应力与加工应力耦合作用下表面残余压应力降低为-92.8 MPa,距离表面0.2 mm处达最大值-131.3 MPa。由此可知Z方向应力分量在毛坯应力作用下表面残余应力降低约15.3%,次表面残余应力降低约2.9%;以仅毛坯应力作用下应力状态为基准,毛坯应力与加工应力耦合作用下表面残余应力提高约17.6%,次表面及芯部残余应力幅值基本接近。
综上所述,对于X方向残余应力分量毛坯应力与加工应力会导致工件全厚度范围内应力变大;而对于Z方向应力分量,初始应力主要造成表面应力改变,仅毛坯应力会导致表面压应力减小,加工应力会导致表面压应力增大。
4 滚压过程中应变-应力场演变
在薄壁工件双侧滚压过程中,随外部能量输入滚轮逐渐压入工件,表层材料被迫产生弹性变形,同时产生接触应力,当应力达弹性极限后,随着滚轮的碾压作用材料发生压缩或拉伸塑性变形。在卸载后由于塑性变形的作用,材料内部变形状态不协调,周围未发生塑性变形的材料对已变形材料产生弹性约束,滚压及其临近区域被迫产生拉伸或压缩弹性变形,从而产生局部应力。在此过程中由于薄壁零件的弱刚度特性,工件整体在滚压后会发生弯曲变形,从而产生附加应力。滚压工件最终的应力场实质为局部应力和附加应力的叠加。而在变形协调过程中有一部分塑性变形被保留下来,仍以残余塑性应变的形式保存在滚压区域金属材料的内部。最初的输入能量经转化分别形成了滚压变形、残余应力和残余塑性应变保留在材料内部,滚压过程中的能量转化过程如图10所示。
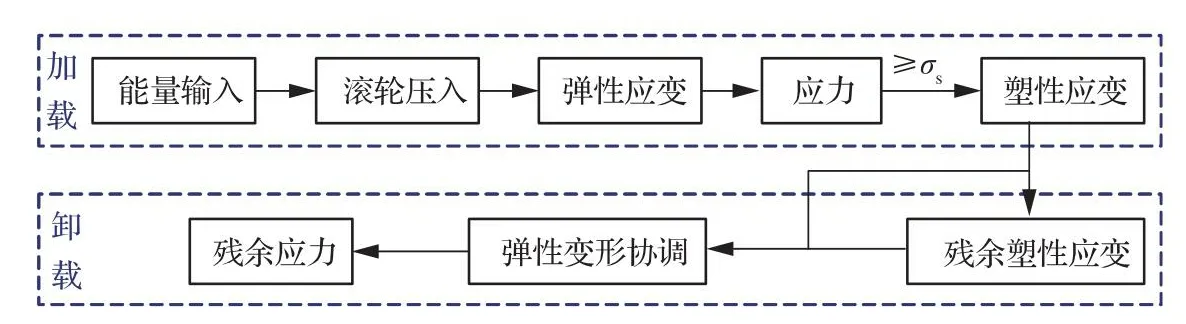
图10 滚压过程中外部能量输入及转化过程Fig.10 External energy input and conversion process during rolling
初始应力的存在改变了滚轮压入过程中的接触应力状态,进而会对后续塑性应变产生影响。为揭示造成3种初始应力状态下滚压变形及残余应力差异的内在原因,对滚压前和滚压过程中的应力状态和塑性应变进行对比分析,提取滚压过程中滚轮滚压位置处的滚压前Mises应力、滚压过程中Mises应力和等效塑性应变(PEEQ)进行分析,如图11所示。
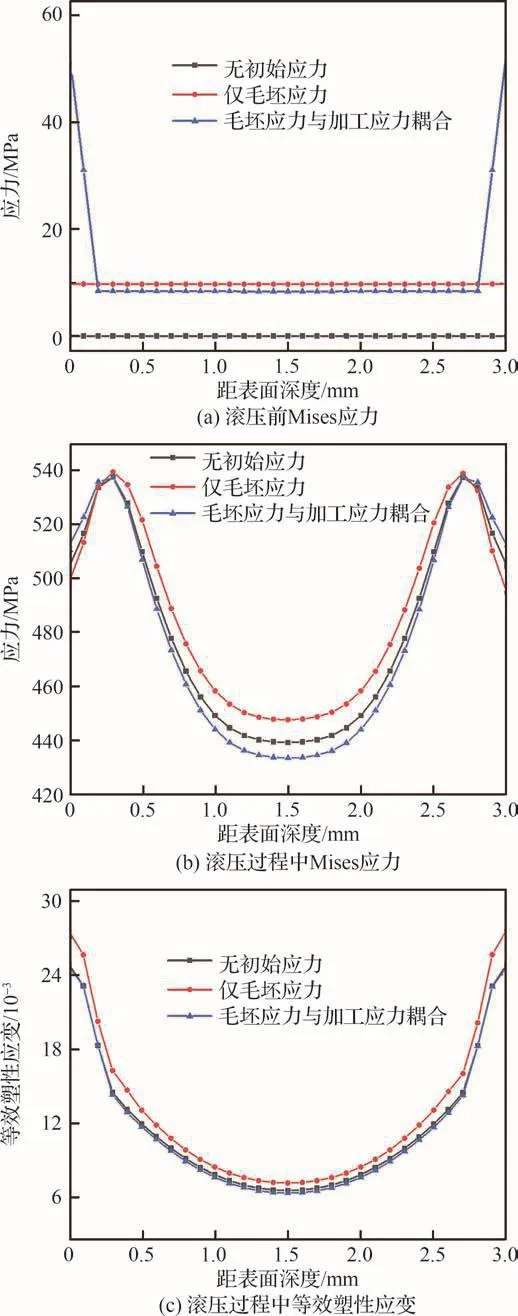
图11 滚压前和滚压过程中的应力及等效塑性应变Fig.11 Stress and equivalent plastic strain before and during rolling
由图7和图11(a)可知初始应力释放后,工件即发生下凹弯曲变形。由于变形导致的附加应力存在,工件整体产生初始应力场。由图11(b)可看出在滚压过程中3种初始应力值、最大值均在工件次表面。由赫兹理论可知滚轮和工件接触属于硬接触,所以滚轮沿压入方向产生的压应力占主导地位,在表面下有高剪应力,故在该深度范围内产生较大的接触应力。如图11(c)所示,仅在毛坯应力作用下工件产生的等效塑性应变最大;在加工应力与毛坯应力耦合作用下等效塑性应变最小。结合滚压完成后3种初始应力状态下的滚压变形可知等效塑性应变与滚压变形具有相同的变化规律。为对塑性应变进行更具体的分析,提取图8中L1迹线滚压完成后的三向等效塑性应变分量如图12所示。

图12 T型件滚压区域中间截面处的三向等效塑性应变分量Fig.12 Three-direction equivalent plastic strain components at middle section of rolling area of T-shaped parts
由图12可见3种初始应力状态下X、Y、Z3个方向的应变曲线均呈对称式分布。在X方向和Z方向,滚压区域材料发生拉伸塑性变形;在Y方向,材料发生压缩塑性变形。此外在X方向和Y方向均呈现出在仅毛坯应力状态下塑性变形最大的规律。换言之仅在毛坯应力的作用下滚压接触应力与初始应力叠加,导致滚压区域材料更易发生塑性变形;而在加工应力作用时由于材料表面在X方向和Z方向存在压应力,材料更难发生拉伸塑性变形,导致整体产生的塑性变形较小。
对于薄壁工件的双侧滚压过程,工件内部存在弹性应变、塑性应变、应力等多个变量,且随外部约束条件变化,各因素间互相协调并最终趋于稳定状态。此外塑性变形的产生和释放及其与周围材料的变形协调是工件内部的主要变化,过程中伴随着工件内部应力的变化,而残余应力则是工件内部变形协调的最终表现形式,工件在滚压完成约束释放前后的变形机制如图13所示。塑性变形区(即滚压区域)在滚压作用下发生沿滚压方向和垂直滚压方向的拉伸塑性变形、沿滚轮压入方向发生压缩塑性变形,导致工件的塑性变形区变得更长、更薄。由于周围材料的约束作用,工件整体呈现上凸弯曲变形,与此同时塑性变形区产生压缩残余应力,而其他区域产生拉伸残余应力;并且随塑性变形程度增大,工件产生更为明显的整体弯曲变形和更高幅值的残余应力。
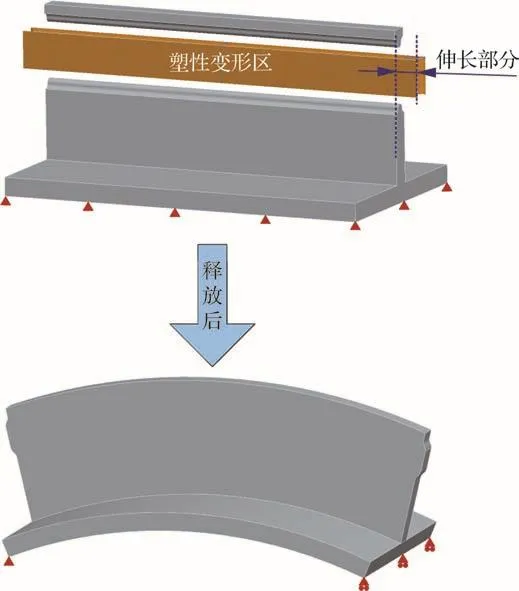
图13 薄壁构件滚压变形示意图Fig.13 Schematic diagram of rolling deformation of thin-walled components
5 结 论
1) 借助有限元分析软件ABAQUS建立了T型件不同初始应力状态下的有限元分析模型,通过试验测得的残余应力数值与有限元仿真结果相比,最大误差为12.87%,验证了有限元模型的正确性。
2) 在无初始应力、仅毛坯应力、毛坯应力与加工应力耦合3种初始应力状态下工件的滚压变形分别为2.56×10-1、2.76×10-1、2.49×10-1mm,以无初始应力状态下的滚压变形为基准,毛坯应力对滚压变形的影响程度约为7.8%,在仅毛坯应力影响基础上加工应力的影响约为9.8%,且毛坯应力与加工应力的作用方向相反。
3) 在3种初始应力状态下滚压区域残余应力主要集中在滚压方向和垂直滚压方向,在工件表面均为压应力,在次表面达到最大值。此外在滚压方向毛坯应力与加工应力会导致工件全厚度范围内应力变大;在垂直滚压方向初始应力主要造成表面应力的改变,仅毛坯应力会导致表面压应力减小,加工应力会导致表面压应力增大。
4) 在毛坯应力作用下滚压区域材料更易发生塑性变形,而加工应力起反作用,且滚压区域的应力分布规律与材料塑性变形和工件的整体变形相关。

