基于晶体塑性理论的高-低周疲劳寿命预测统一准则

王秀锐，李凯尚，谷行行，张勇，陆体文，王润梓，张显程，

1.华东理工大学 教育部承压系统与安全重点实验室，上海 200237

2.东北大学（日本） 工学研究科 断裂与可靠性研究所，仙台 9808579

由于镍基高温合金具有优异的力学性能，被广泛应用于飞机发动机的关键部件，如发动机涡轮盘、叶片、轴以及紧固件等［1］。在运行服役期间各种机械载荷的存在使这些部件处于复杂的工作环境中。频繁地加、卸载引起的疲劳载荷及装配公差引起的振动载荷是导致工程部件失效的主要原因。经统计，工程应用中约80%的故障是由疲劳失效引起的，这给个人和财产安全带来了风险［2-3］。因此对材料进行疲劳寿命的预测是工程部件安全运行的重要手段。

传统的金属疲劳研究通常包括低周疲劳（Low Cycle Fatigue，LCF）和高周疲劳（High Cycle Fatigue，HCF）两个方面。材料发生疲劳失效前经历的循环载荷低于105周次则为LCF，处于105～107周次范围内则为HCF［4-5］。在LCF加载过程中材料承受的应力水平较高，通常通过应变控制加载。在LCF加载过程中材料的变形模式主要是由滑移引起的塑性变形，且塑性变形分布较为均匀。随着疲劳加载的进行，材料的塑性变形量会不断增加，大量的塑性变形会引起裂纹的萌生、扩展直至断裂。而在HCF加载过程中材料承受的应力水平较低，一般通过应力控制加载。较低的应力加载水平使材料产生局部的微塑性变形，局部微塑性变形的累积也会导致裂纹的萌生及扩展，直到材料发生疲劳失效。

在结构强度方面提出了金属材料的多种疲劳寿命预测模型，可分为宏观和介观两个类型，具体又可分为用于预测HCF寿命的和用于预测LCF寿命的两种。其中在宏观水平上包括由Basquin［6］、Morrow［7］、Goodman［8］提出的基于应力准则的寿命预测模型，多用于HCF寿命预测。而Manson［9］和Coffin［10］提出的基于应变准则的寿命预测模型多用于LCF寿命预测。尽管在宏观水平上已提出能同时预测LCF和HCF寿命的统一准则［11］，但模型却很难与微观损伤关联。然而在介观水平上，将晶体塑性理论模型与有限元方法结合可有效提取材料的微观演化特征，即疲劳指示因子（Fatigue Indicator Parameter，FIP）［12-14］。这样的方法又被称为晶体塑性有限元（Crystal Plasticity Finite Element，CPFE）方法。晶体塑性不仅可揭示介观尺度下滑移主导的变形机制，还可借助FIP实现疲劳寿命预测［12-13］。此外诸多学者提出了晶粒水平上FIP的表征方法，如基于累积塑性滑移［12］、应变能耗散［15］、应变统计学理论［16］、驻留滑移带能量［17］的FIP，这些FIP多用于LCF寿命预测。其中应用较多的FIP主要包括累积塑性滑移P［13，18-20］和累积能量耗散W［13-14，20］。基于累积损伤的寿命预测准则甚至能用于预测材料的HCF寿命［21］。

目前在CPFE框架下，虽基于累积塑性滑移P和累积能量耗散W的FIP能较为准确地预测材料的LCF寿命，但对HCF寿命的预测仍有较明显的误差，且能同时预测材料的HCF和LCF寿命的准则也较少。因此本文的主要工作就是基于现有的FIP做出改进，使基于提出的新FIP建立的模型不仅能准确预测材料的LCF寿命，还能准确预测材料的HCF寿命。此外考虑在HCF和LCF加载过程中材料内部都会产生滑移主导的塑性变形，且在HCF加载过程中材料的塑性变形存在于局部的某些晶粒中，宏观水平上的材料变形几乎处于弹性阶段［14，22-23］。本文选用在介观尺度上能捕捉到微观损伤演化的寿命预测模型对统一准则展开探究。在累积能量耗散W的基础上考虑有效弹性能Eel，建立了一个新的FIP有效能Eeff，并基于有效能Eeff建立了能较准确预测镍基合金LCF和HCF寿命的统一准则。本文先介绍所用试验数据的来源，包括所研究材料LCF到HCF的整个范围；然后描述关于晶体塑性本构的理论及基于晶体塑性理论对LCF到HCF统一寿命的预测准则；接着通过经典的FIP累积能量耗散W和新的FIP有效能Eeff预测LCF和HCF寿命。

1 LCF到HCF寿命预测的材料基础

研究的材料为镍基合金Inconel 718（IN718），因其与GH4169具有相同的化学成分和力学性能，在一些文献中被看作一种材料［22，24］。图1（a）［25-30］～图1（c）［25-36］为室温加载条件下IN718的加载应变幅Δεt、应力幅Δσ与疲劳寿命之间的关系。相应地表1［25-36］列出了镍基合金IN718的LCF和HCF寿命试验数据。图1（a）中显示了应变控制加载得到的59个LCF试验数据点，其中应变加载范围Δεt= ±0.34% ～±2.5%，可看出LCF寿命随加载应变幅增加呈现下降趋势。图1（b）［31-36］为应力控制加载得到的56个HCF试验数据点，其中最大应力幅范围σmax=330 ～ 690 MPa。随应力幅值增加HCF寿命呈轻微下降趋势。为获得镍基合金IN718由LCF到HCF试验寿命的总体变化趋势，合并图1（a）和图1（b）两种控制模式下的试验寿命数据。由于HCF加载过程中材料内部的塑性变形非常小，在宏观水平上几乎处于弹性阶段［22-23］。根据胡克定律将可将图1（b）中的应力-循环次数（S-N）曲线转化为应变-循环次数（E-N）曲线［37］，从而得到图1（c）所示的包含研究材料由LCF到HCF寿命的E-N曲线，其中应变范围Δεt= ±0.17% ～ ±2.5%。在LCF到HCF整个寿命范围内，应变幅与疲劳寿命间的变化规律符合反比例函数。此外通过文献可得图1（d）所示的室温加载条件下镍基合金IN718的S-N曲线，可知其疲劳极限σlimit为330 MPa［35］。

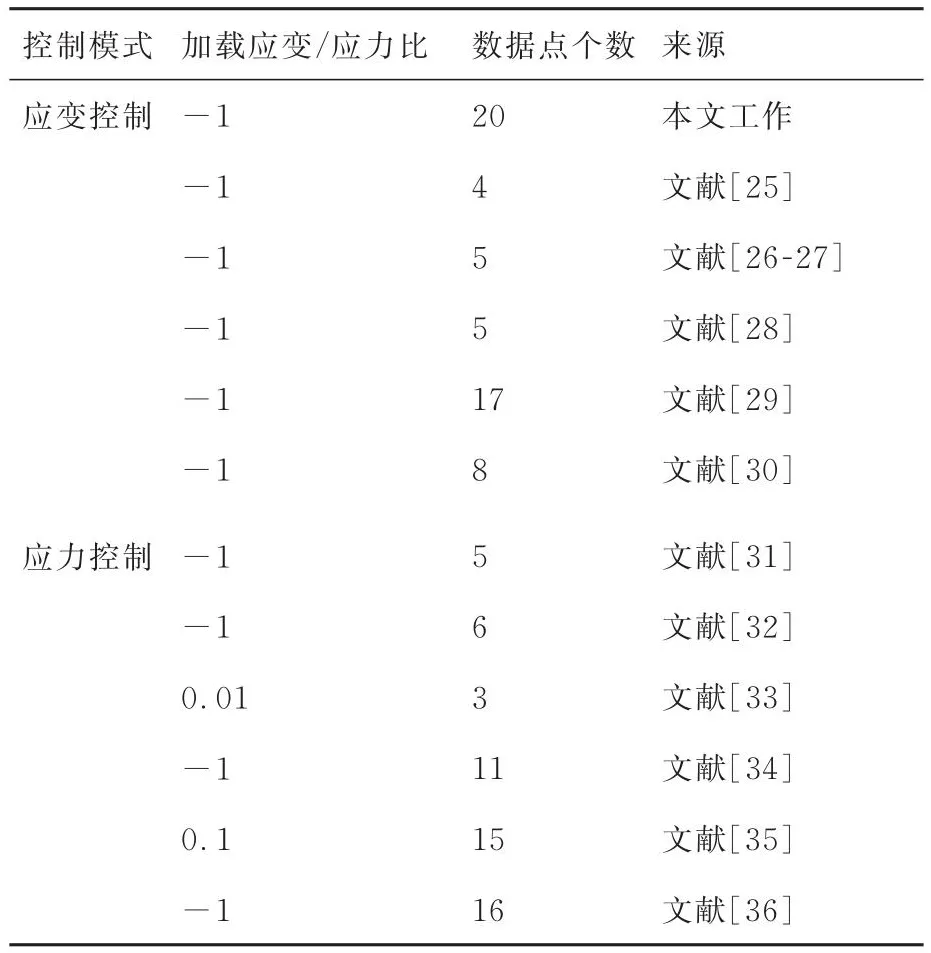
表1 关于镍基合金IN718的LCF和HCF寿命试验数据Table 1 Experimental data of LCF and HCF lifes for nickel-based alloy IN718

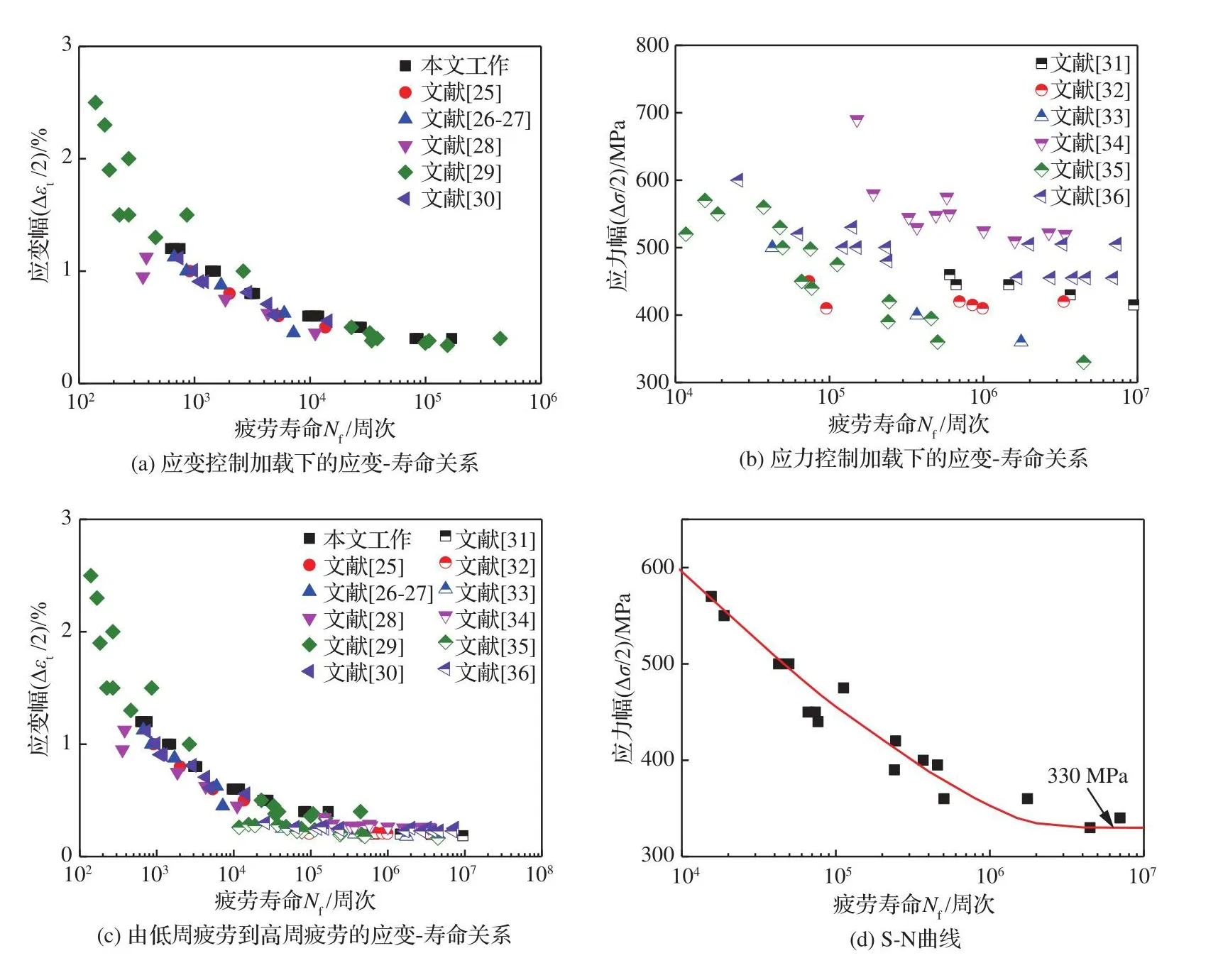
图1 室温加载条件下镍基合金IN718的低周疲劳、高周疲劳试验寿命相关数据及S-N曲线Fig.1 Correlative experimental life data of low cycle fatigue， high cycle fatigue and S-N curve for nickel-based alloy IN718 under room temperature loading condition

2 CPFE的理论基础

2.1 晶体塑性本构模型

晶体塑性理论是由Rice［38-39］及Peirce［40］等提出的。总变形梯度F包含弹性变形梯度和塑性变形梯度，用乘法分解表示为

式中：Fe为由晶格弹性拉伸和旋转引起的变形梯度；Fp为塑性变形梯度。塑性速度梯度Lp可表示为

式中：γ̇α为α滑移系上的晶体塑性滑移率；sα和mα分别为α滑移系上的滑移方向向量和滑移面法向向量；n为总滑移系数，面心立方（Face-Centered Cubic， FCC）合金的非弹性变形是由12个八面体滑移系（｛111｝〈110〉）的激活控制的，因此n=12［12，14，20］；⊗表示张量的并矢积。对于α滑移系，用热激活流动法则［41］描述γ̇α：

基于Li等［42］的工作，α滑移系上的解析剪切应力τα可表示为

式中：T*为第二Piola-Kirchoff应力；ζ为弹性刚度张量；Εe为当前的弹性张量； “：”表示张量的双重收缩。因此Sα定义为

式中：N为疲劳循环次数；hαβ为硬化模量矩阵中的元素，表示滑移系α和β之间的交叉硬化行为；Ssat和S0分别为饱和滑移阻力和初始滑移阻力。hαβ定义为

式中：hs为硬化常数；w为潜在硬化比；δαβ为克罗内克尔符号。在CPFE框架下，Armstrong-Frederick运动硬化准则可被用于描述滞后回线［43］。背应力Bα可表达为

2.2 基于晶体塑性的经典FIP

采用经典FIP累积能量耗散W对镍基合金IN718进行疲劳损伤评估与疲劳寿命预测［13，20，44-45］。累积能量耗散W与解析剪切应力τα及晶体塑性滑移率γ̇α有关［18，45］，可表示为

式中：hB和rD分别为硬化常数和动态恢复参数。

式中：t为晶体塑性滑移时间。设Wcrit为累积能量耗散临界值，是一个对于给定材料在给定温度下与加载条件无关的常数［12-13，45］。一旦累积能量耗散临界值Wcrit确定，疲劳寿命就可通过式（10）最终确定：

式中：Nf为试验疲劳寿命；为第i周次的累积能量耗散。

2.3 基于新FIP预测LCF到HCF寿命的统一准则

根据S-N曲线可知对材料施加的应力降低至一定值（即疲劳极限值σlimit）后材料的疲劳寿命被认为是无限大的。将加载应力大于疲劳极限σlimit的部分定义为有效应力，有效应力在材料的LCF/HCF加载过程中造成的疲劳损伤定义为有效疲劳损伤，如图2中的绿色阴影所示。图2中的蓝色阴影面积表示有效弹性能，是有效应力加载造成的有效弹性损伤。图2中的黄色线段表示有效弹性应变εel，疲劳极限和滞后回线中最大应力间的差值为Δσ，则每周次的有效弹性能Eel-cyc可通过式（11）确定：

图2 滞后回线中的有效弹性能示意图Fig.2 Schematic diagram of effective elastic energy in hysteresis loop

式中：εel-cyc为每周次的有效弹性应变。

由第1节可知镍基合金IN718的疲劳极限为330 MPa，结合滞后回线可确定有效弹性能的大小，进而确定有效弹性能的值。在累积能量耗散的基础上考虑有效弹性能，定义一个新的FIP，即有效能Eeff。其表达式可写为

式中：Eel为有效弹性能，是有效能Eeff的弹性部分；Epl为塑性变形过程中产生的累积能量耗散，即W，为有效能Eeff的塑性部分。假设随循环周次增加，有效能的叠加会达到一个定值，这个定值对于给定材料在给定温度下与加载条件无关。则有效能临界值Ecrit一旦确定，疲劳寿命就可最终确定：

2.4 代表性体积单元模型

为获得镍基合金IN718在晶粒水平上的力学行为用于确定并验证其材料参数，采用泰森多边形方法（VT法）建立了晶体塑性代表性体积单元（RVE）模型。RVE模型可用来描述材料的宏观力学行为。如图3（a）所示（图中RP为参考点），RVE模型大小为0.2 mm × 0.2 mm，晶粒个数为200，平均晶粒尺寸与图3（b）（图中Dˉ为材料在EBSD观察下统计的平均晶粒尺寸）中标准热处理后IN718的实际平均晶粒尺寸相等，即14.1 μm。

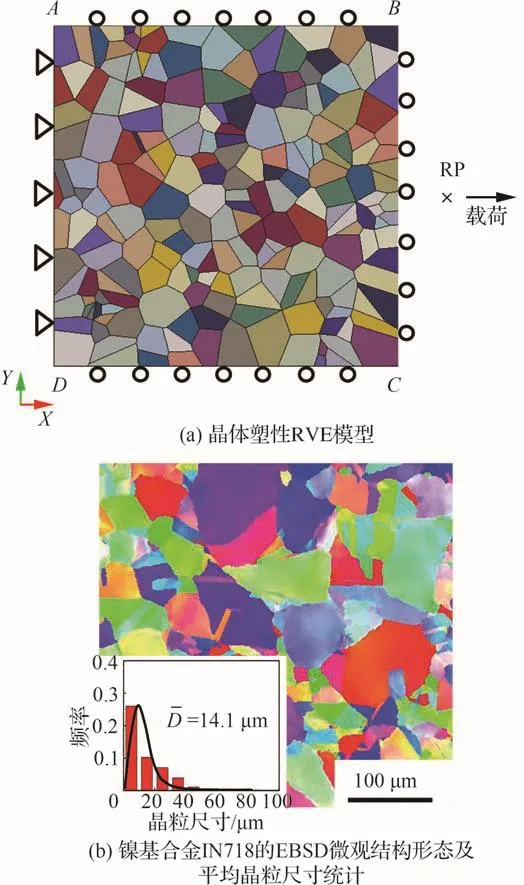
图3 RVE模型及镍基合金IN718的平均晶粒尺寸统计图Fig.3 RVE model and average grain size statistics diagram of nickel-based alloy IN718

平面应变的RVE二维模型的坐标与约束条件已在图3（a）中标明。RVE模型左边界的所有节点在X方向上的位移被约束，且被允许在Y方向上自由移动；模型中上边界所有节点和下边界所有节点在Y方向上施加多点约束，右边界和参考点RP之间在X方向上施加多点约束，这样可使上下边界的节点在Y方向上有相同的位移，右边界和参考点RP在X方向上有相同的位移。通过在参考点RP上施加周期性位移载荷可实现右边界在X方向上的周期性位移加载。这样的约束方式可使介观尺度上具有一定晶粒数量的RVE模型准确预测材料的力学行为［13，46］。

3 结果和讨论

3.1 模型参数的标定和验证

本构模型中的CPFE材料参数可分为各向异性弹性常数、流动参数和硬化参数3类，具体见表2。

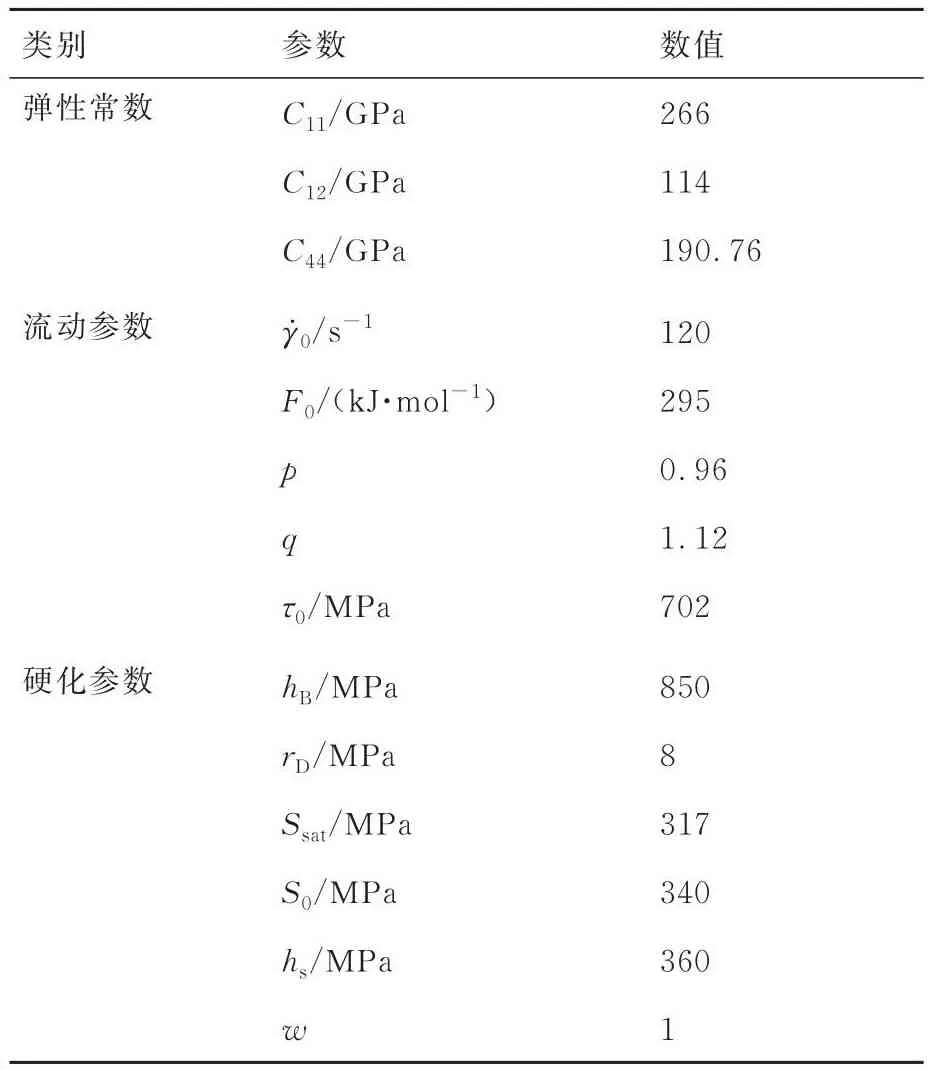
表2 晶体塑性模型的材料参数Table 2 Material parameters in crystal plasticity model

首先通过拉伸试验确定IN718的弹性模量E和泊松比ν的大小。由于镍基合金IN718以镍为基体，故其各向异性系数A参考晶体Ni，取为2.51［19，47］。然后根据式（14）～式（16）计算各向异性弹性常数C11、C12和C44［19，48］：

此外，流动参数γ̇0和F0可先利用有关镍基合金文献中的数据确定［41，49-51］，如表2所示。剩余的流动参数（p、q、τ0）和硬化参数（hB、rD、Ssat、S0、hs、w）可先在文献的推荐范围中选取一个初始值［41，49-51］，然后采用试错法利用试验获得的镍基合金拉伸曲线将这些参数重新标定［16，19］。从图4的拉伸曲线可看出模拟的拉伸曲线与试验曲线间吻合良好。所有标定后的晶体塑性模型参数列于表2。

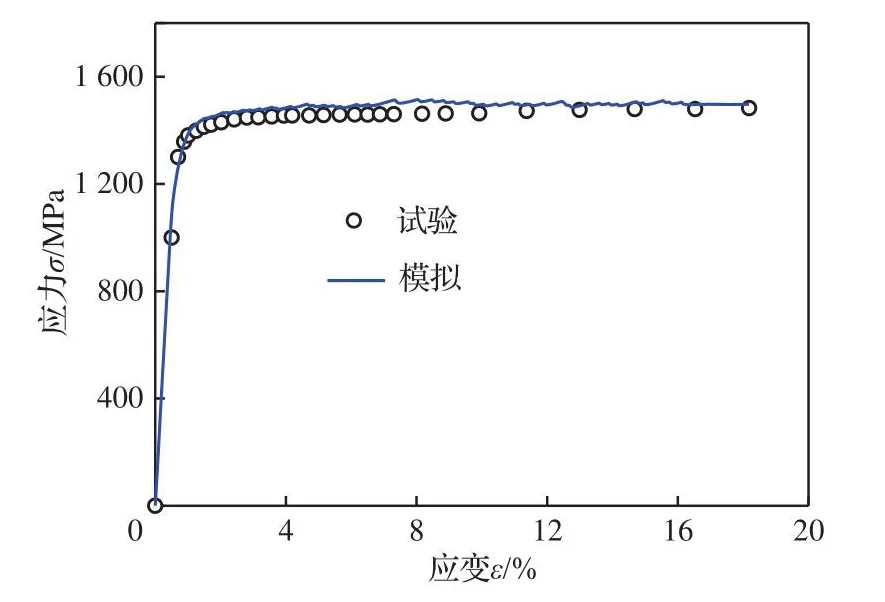
图4 模拟和试验数据的拉伸曲线拟合Fig.4 Tensile curve fitting between simulated and experimental data

CPFE模型参数标定后，通过对比材料相同工况下的模拟与试验应力-应变曲线完成模型参数的验证。其中模拟的应力-应变曲线数据是通过RVE模型的CPFE分析得到的。模拟与试验的第一周滞后回线对比结果如图5所示，其中实线与符号分别表示±0.8%、±1.0%和±1.2%3种加载应变幅下模拟和试验的第1周滞后回线。图5证明3种应变幅下的模拟结果和试验结果吻合较好。

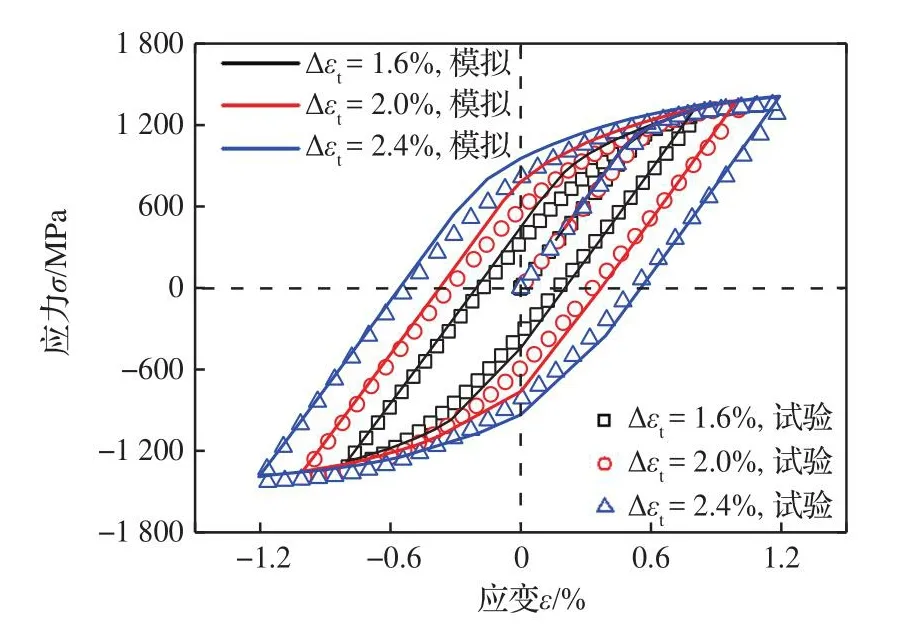
图5 模拟和试验数据的第1周滞后回线拟合Fig.5 The first cycle hysteresis loops fitting between simulated and experimental data

3.2 CPFE模型的敏感性分析

3.2.1 网格敏感性

为排除网格效应对CPFE分析的影响，建立了4种具有不同网格尺寸的RVE模型进行网格敏感性分析。其中4种不同的网格尺寸分别为0.001、0.002、0.004、0.010 mm。如图6所示，随网格尺寸的增加，RVE模型模拟的拉伸曲线与试验拉伸曲线之间的空隙越来越大。其中具有中等网格尺寸（0.002 mm）和细网格尺寸（0.010 mm）的RVE模型模拟的拉伸曲线与试验拉伸曲线间吻合较好，且在具有中等网格尺寸和细网格尺寸的RVE模型云图中，两者的最大累积能量耗散位置一致。考虑数值计算过程中的计算成本，选用具有中等网格尺寸的RVE模型进行CPFE模拟。

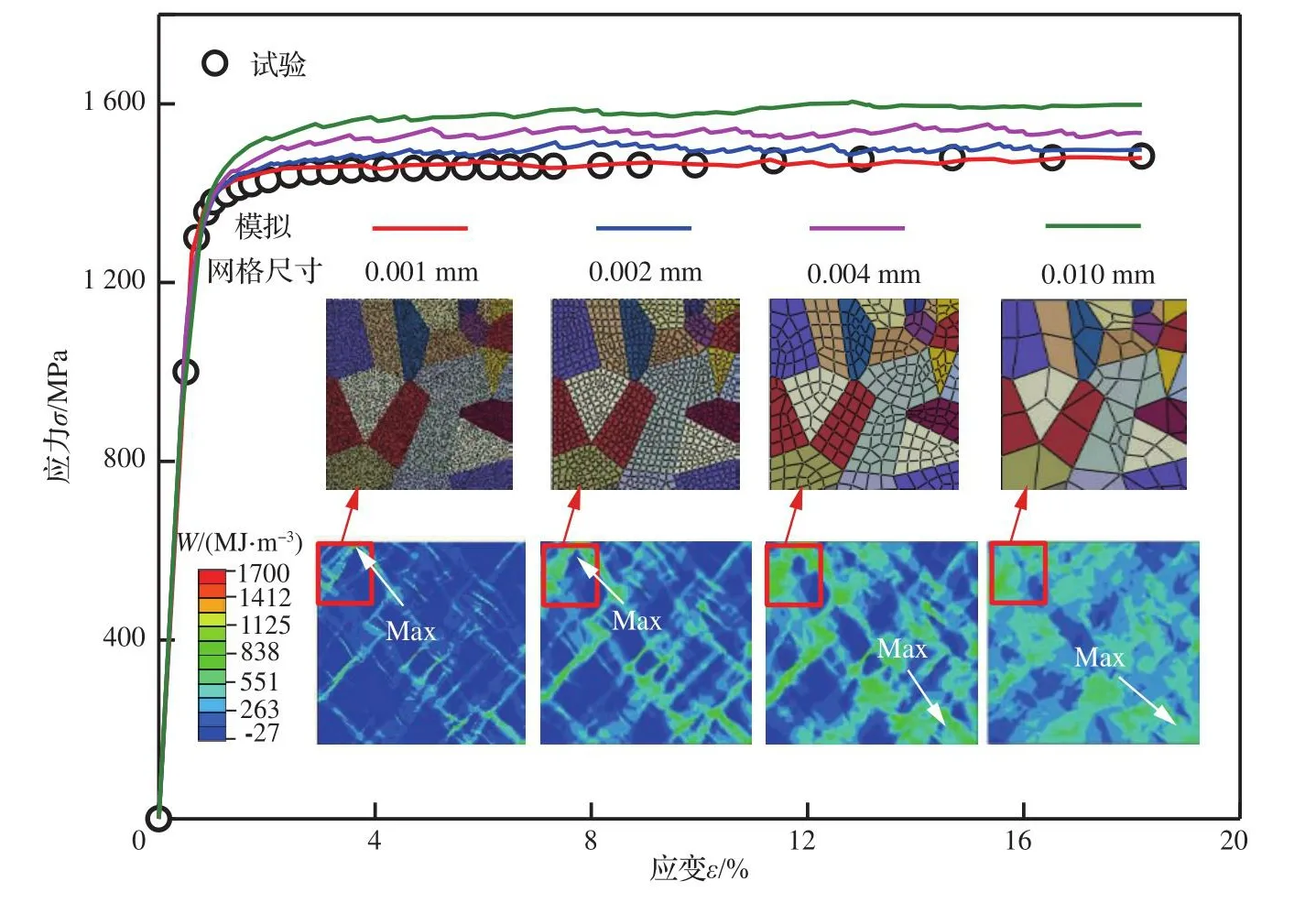
图6 4种不同网格尺寸的RVE模型模拟的拉伸曲线与试验曲线结果对比Fig.6 Results contrast between tensile curves simulated by RVE models with four different mesh sizes and experimental tensile curve

3.2.2 微观结构敏感性

为对CPFE模型进行包括晶粒结构和晶粒取向在内的微观结构敏感性分析，采用3.2.1节中选用的具有中等网格尺寸（0.002 mm）的RVE模型展开工作。如图7所示，4种不同的微观结构模型M1、M2、M3、M4模拟的拉伸曲线和试验拉伸曲线结果吻合良好。且4种微观结构局部的能量耗散带相对于加载方向约为45°，呈现出共同的局部模式。因此可排除不同微观结构在CPFE模拟中产生的偏差影响。

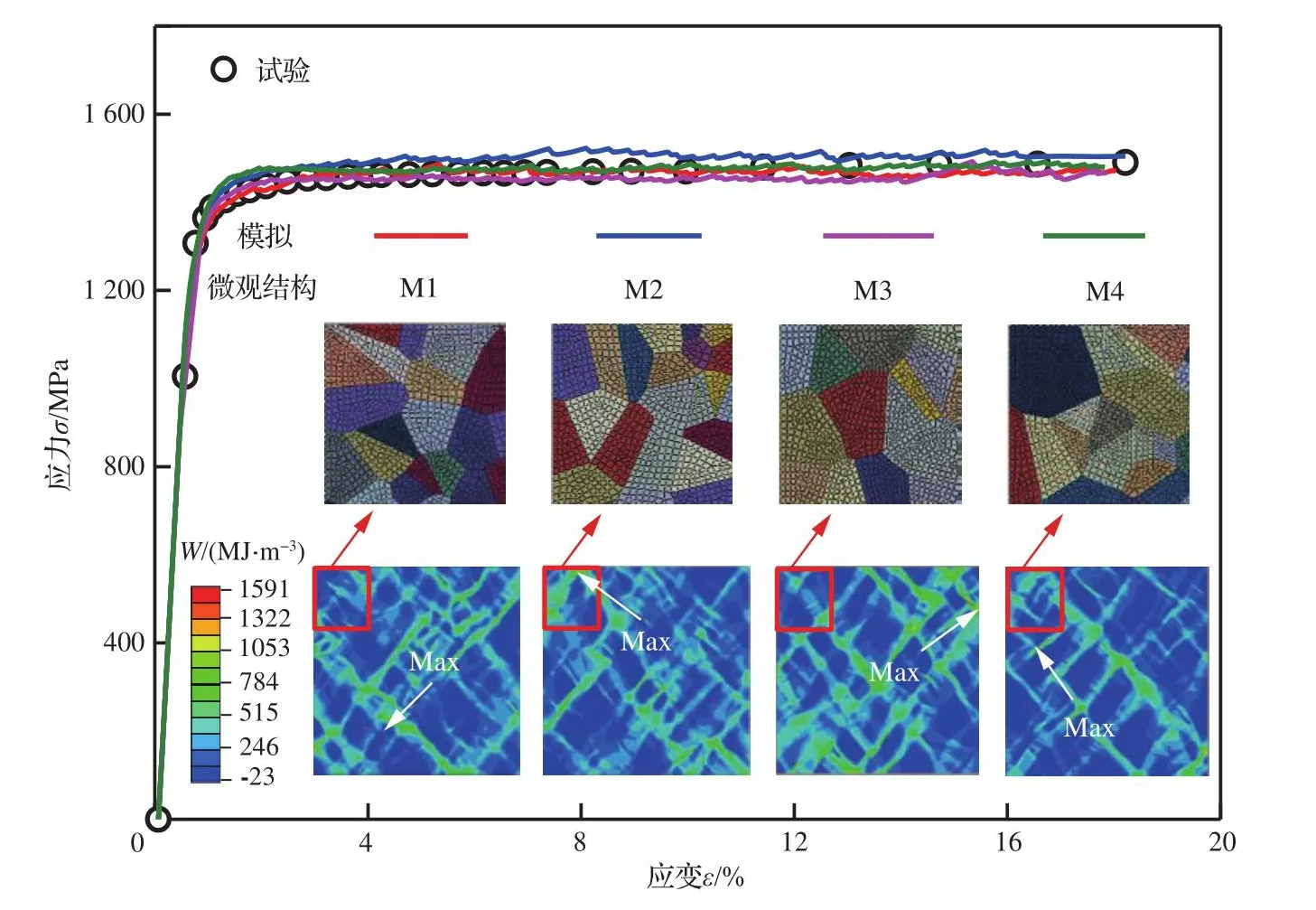
图7 4种不同微观结构的RVE模型模拟的拉伸曲线与试验曲线结果对比Fig.7 Results contrast between tensile curves simulated by RVE models with four different microstructures and experimental tensile curve

3.3 FIP临界值确定

3.3.1 累积能量耗散临界值

能量耗散临界值的确定需要同种工况下的模拟和试验数据。模拟工作涉及的应变幅值包括±0.35%、±0.40%、±0.45%、±0.50%、±0.60%、±0.80%、±1.00%、±1.20%、±1.60%、±2.00%。图8（a）和图8（b）分别为累积能量耗散W随循环周次的变化及每周次累积能量耗散Wcyc的变化情况。需要注意的是由于±0.35%、±0.40%、±0.45% 3种应变幅下能量耗散的累积量过小，接近于0，图8（a）和图8（b）中的3条曲线非常接近，通过局部放大图进行进一步展示。由图8（a）可见累积能量耗散随循环周次增加呈近线性趋势增加，可认为在镍基合金IN718的加载过程中能量耗散的累积速率是恒定的。将这一变化规律考虑进来，式（10）可进一步表达为

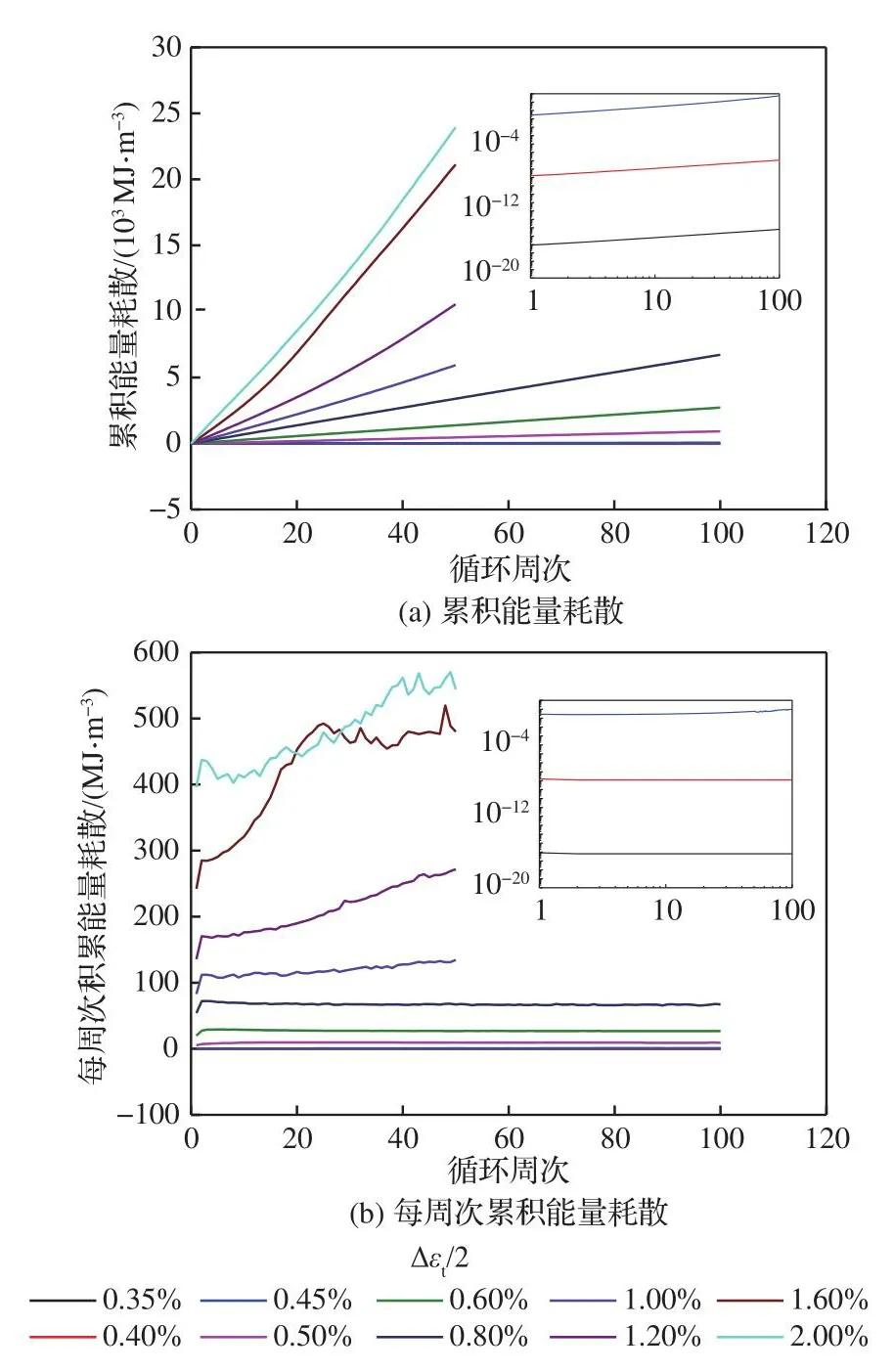
图8 各应变幅下累积能量耗散及每周次的累积能量耗散变化曲线Fig.8 Variation curves of accumulated energy dissipation and accumulated energy dissipation per cycle for various amplitudes

式（17）需要一种工况下的试验寿命确定累积能量耗散临界值Wcrit。此外在图8（b）中可见较低应变幅下Wcyc随循环周次的变化相对稳定。考虑计算时间和计算成本的问题，将较高应变幅下的模拟周次定为50。此外在较高应变幅下，Wcyc随循环周次的变化最终也是趋于稳定的。

3.3.2 有效能临界值

有效能Eeff是在累积能量耗散W的基础上考虑有效弹性能Eel而定义的新FIP。由3.3.1节可知每种应变幅下累积能量耗散W随循环周次增加而近线性增加。即每循环一个周次，能量耗散的累积量可被近似看作一个定值。此外如图9（a）所示，随循环周次增加，有效弹性能Eel的累加也呈近线性趋势。那么根据式（12）与线性相加准则可知，有效能随循环周次增加也呈近线性增加的趋势，对±0.35%、±0.40%和±0.45% 3种应变幅下的曲线进行局部放大展示，如图9（b）所示。则式（13）可进一步表达为

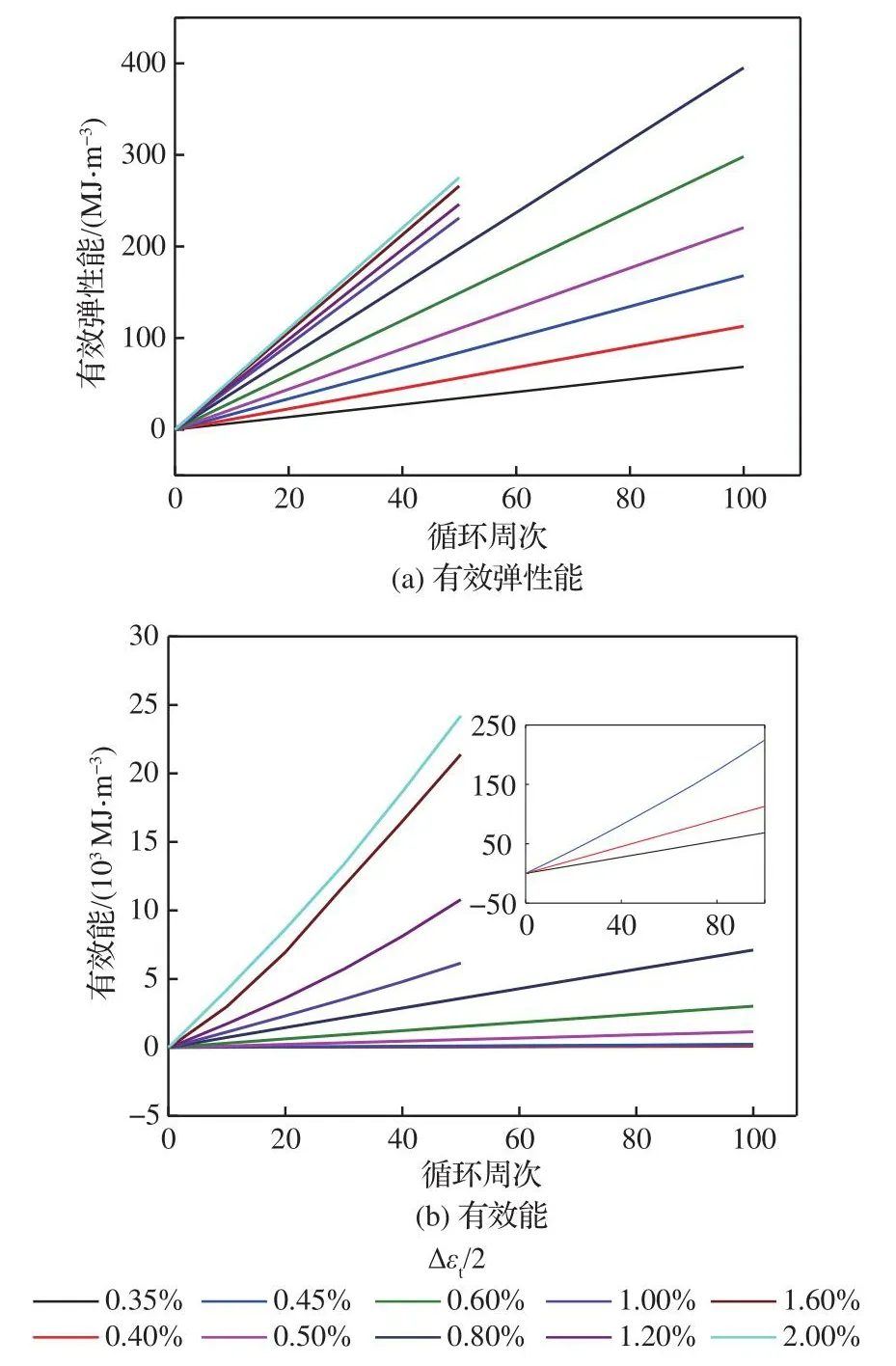
图9 各应变幅下有效弹性能和有效能随循环周次的变化曲线Fig.9 Variation curves of effective elastic energy and effective energy with number of cycles for various amplitudes

与累积能量耗散临界值Wcrit类似，需要一种工况下的试验寿命确定Ecrit的具体值，进而预测其他工况下的疲劳寿命。

3.3.3 临界有效能的进一步修正

基于累积能量耗散临界值Wcrit是一个对于给定材料在给定温度下与加载条件无关的常数这一假设，可有效预测材料的疲劳寿命［12-13，20］。然而如图10（a）所示，±0.35%和±0.40%两个低应变幅下的累积能量耗散临界值Wcrit接近于0，使其在整个加载范围内各个应变幅下的累积能量耗散临界值Wcrit并不相等，且整个加载范围内Wcrit的变化规律不明显。图10（b）所示为各应变幅下有效能临界值Ecrit。与累积能量耗散临界值不同的是有效能临界值Ecrit虽不是定值，但在整个加载范围内随应变幅增加呈先增加后相对稳定的趋势。重要的是有效能临界值Ecrit与每周次有效能Eeff-cyc呈双对数线性关系，如图10（c）所示。将图10（c）中的关系代入式（18）可得［14］：

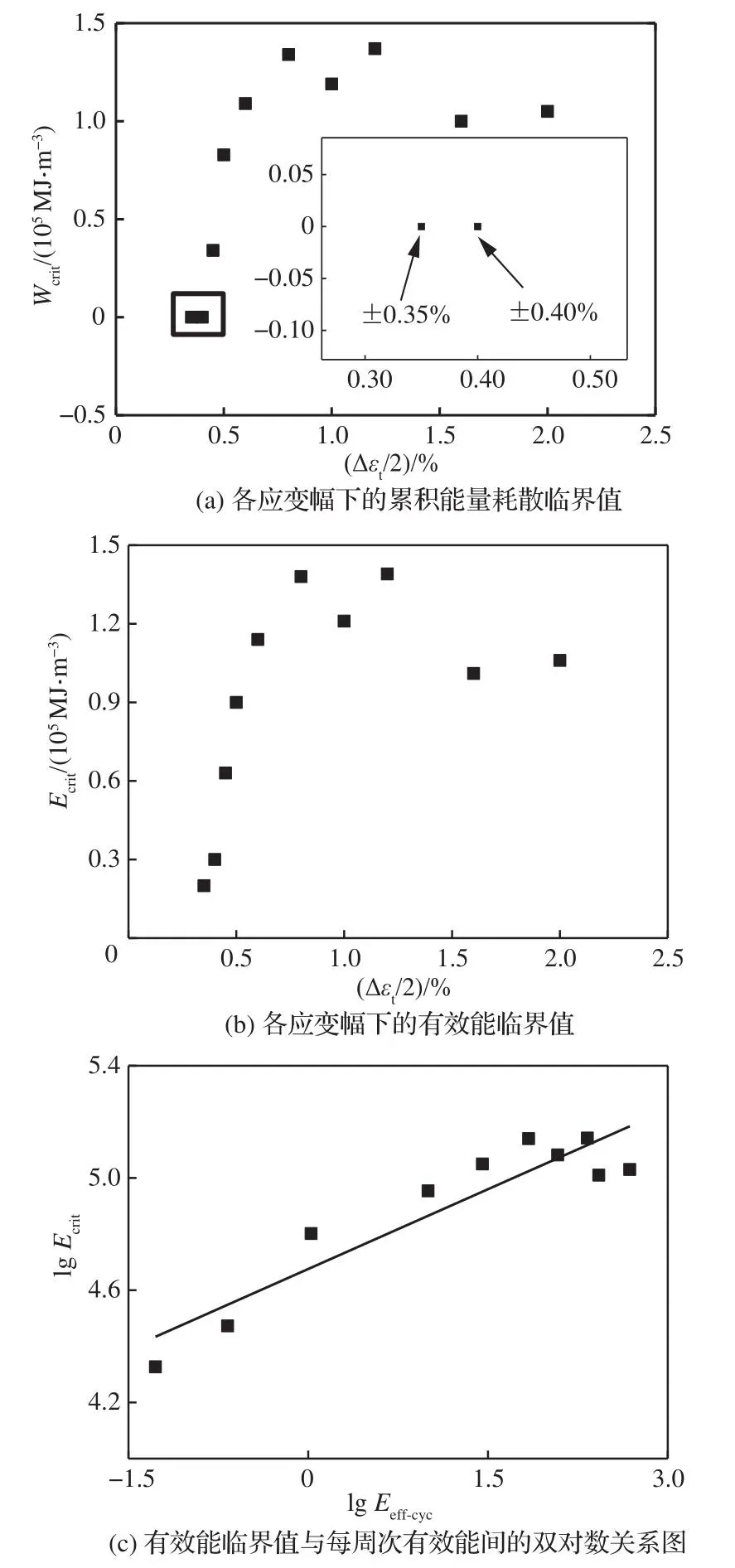
图10 累积能量耗散临界值及有效能临界值相关图Fig.10 Correlative graphs of critical values for accumulated energy dissipation and effective energy critical values

式中：m为指数常数；为修正的有效能临界值，上标“NL”表示非线性。和m可通过两种工况下的数据计算得到。此外表3给出了计算各应变幅下的Wcrit和Ecrit时所用的Wcyc、Eeff-cyc及相应的镍基合金疲劳寿命。

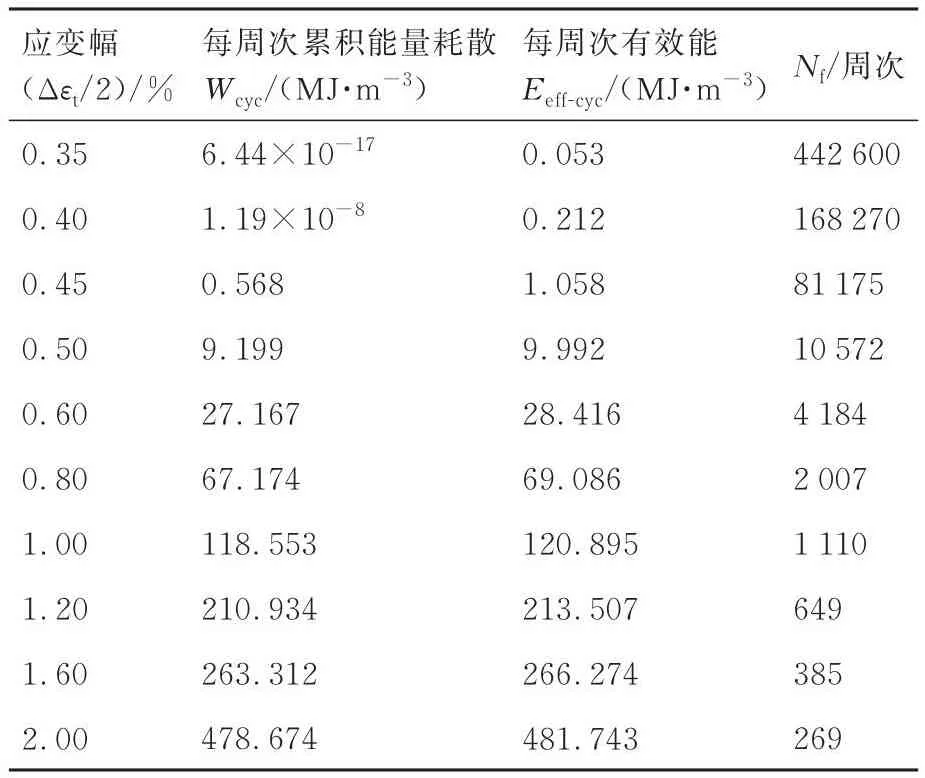
表3 计算镍基合金各应变幅下的Wcrit和Ecrit时所用的Wcyc、Eeff-cyc及疲劳寿命NfTable 3 Adopted Wcyc， Eeff-cyc and fatigue life Nf for calculating Wcrit and Ecrit of nickel-based alloy for various amplitudes

3.4 基于统一准则寿命预测结果的先进性

重点讨论基于累积能量耗散W的寿命预测准则（式（17））、基于有效能Eeff修正前的寿命预测准则（式（18））及基于修正后的寿命预测准则（式（19））预测的疲劳寿命间的对比。选取Δεt=±0.8%分别计算Wcrit和Ecrit，并选取±2.0%（LCF范围）与±0.35%（HCF范围）两个代表性应变幅计算和m。分别根据式（17）～式（19）计算其他应变幅下的疲劳寿命，计算结果如图11（a）和图11（b）所示，图11（b）中的试验寿命参考表3。

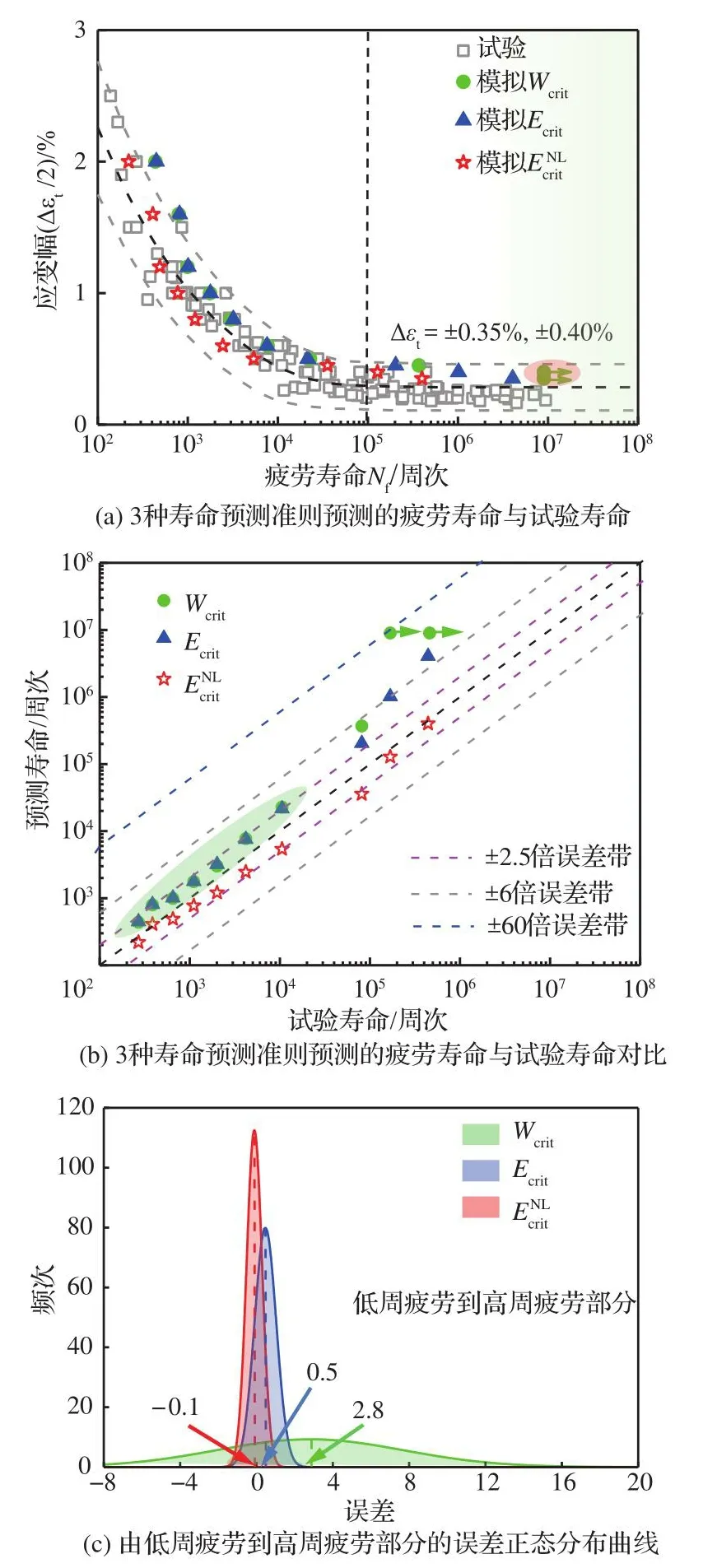
图11 预测疲劳寿命与试验疲劳寿命对比及误差分析Fig.11 Results comparison between predicted fatigue life and experimental fatigue life and error analysis

结合图11（a）和图11（b）可看出基于式（17）预测的LCF寿命与试验寿命吻合较好，基本落在±2.5倍误差带内。然而如图11（a）椭圆框中圆形符号所示，基于式（17）预测的±0.35%与±0.40%两种应变幅下的HCF寿命达到了1012周次甚至更高，落在±60倍误差带内，过于非保守。说明基于累积能量耗散W预测的HCF寿命准确性偏低。结合式（17）和表3可知基于累积能量耗散预测的HCF寿命偏高的原因在于低应变幅下每周次的能量耗散累积量偏低。在累积能量耗散W的基础上考虑有效弹性能Eel定义的新FIP有效能Eeff弥补了这一缺点。如图11（a）和图11（b）中三角符号所示，基于有效能修正前的准则式（18）与基于累积能量耗散W的准则式（17）对LCF寿命的预测能力相近，但式（18）预测的HCF寿命基本落在±6倍误差带范围内，说明有效能Eeff对HCF寿命的预测能力高于累积能量耗散W。此外由图11（a）可看出基于式（19）预测的疲劳寿命相比式（18）和式（17）预测的疲劳寿命更接近中间虚线。且由图11（b）可看到基于式（19）预测的LCF和HCF寿命基本落在±2.5倍误差带内，说明其对IN718的LCF到HCF的寿命预测能力有进一步提高。因此对于镍基合金LCF到HCF寿命的预测能力，式（19）高于式（18），式（18）又高于式（17）。

由于图11（b）中每种应变幅下的试验寿命只选取一个数据点，而对于每种寿命预测准则，每种应变幅下的一个预测寿命点可能对应多个试验寿命点。为更准确地量化分析基于式（17）～式（19） 3种准则预测的疲劳寿命准确性和稳定性，对LCF到HCF整个寿命范围中的预测寿命与试验寿命间的误差做了正态分布曲线分析，结果如图11（c）所示。式（20）给出了误差的计算方法，误差即为每种应变幅下的预测寿命与试验寿命的对数差。

式中：Err为误差；Npre和Nexp分别为预测寿命和试验寿命。需要注意的是图11（c）是将每种寿命预测准则中的每个应变幅下所有误差进行统计。其中误差正态分布曲线的均值越接近0，预测的寿命准确性越高；正态分布曲线宽度越窄，预测寿命的稳定性越好。

如图11（c）所示，对于镍基合金IN718的LCF到HCF整个寿命范围，基于式（17）～式（19） 3种准则预测的寿命误差均值分别为2.8、0.5和-0.1。经估计，相比于式（17），式（18）的寿命预测准确性提高了约82%，而式（19）相比于式（18）寿命预测准确性提高了约80%，表明在LCF到HCF整个寿命预测范围内由式（19）预测的疲劳寿命准确性是最高的。且通过三者曲线宽度可知由式（19）预测的疲劳寿命稳定性也是最好的。式（17）预测的疲劳寿命准确性与稳定性最差。值得注意的是图11（c）的分析结果与图11（b）一致。

4 结 论

在介观尺度下将晶体塑性理论和有限元技术相结合，提出了一种高-低周疲劳寿命预测统一准则。即在累积能量耗散W的基础上考虑有效弹性能Eel定义了一个新的疲劳指示因子有效能Eeff。并通过对比基于不同疲劳指示因子的寿命预测准则验证该统一准则的预测能力，得到的主要结论如下。

1） 基于累积能量耗散W的寿命预测准则可较好地预测镍基合金Inconel 718的低周疲劳寿命，但其预测的高周疲劳寿命达到了1012周次甚至更高，过于非保守。

2） 基于累积能量耗散引入有效弹性能组成了新疲劳指示因子，即有效能Eeff。与基于累积能量耗散W的寿命预测准则相比，基于有效能Eeff修正前的寿命预测准则对镍基合金Inconel 718从低周疲劳到高周疲劳寿命的预测准确性和稳定性都有提高，其中准确性提高了约82%。

3） 相比于基于有效能修正前的寿命预测准则，基于有效能修正后的寿命预测准则对镍基合金Inconel 718从低周疲劳到高周疲劳寿命的预测准确性和稳定性都有进一步提高，其中准确性提高了约80%。重要的是基于有效能Eeff可良好地建立关于镍基合金Inconel 718由低周疲劳到高周疲劳的寿命预测统一准则。