MIMO 窄带加宽带非高斯随机振动试验

马益，贺旭东，陈怀海，郑荣慧

南京航空航天大学 航空航天结构力学及控制全国重点实验室，南京 210016

振动环境试验是检验产品结构可靠性的常用手段［1-3］。传统的单输入单输出（Single-Input Single-Output，SISO）振动试验技术在模拟动力学环境时存在诸多缺点，如局部应力过大、推力不足等。相较于SISO 情形而言，多输入多输出（Multi-Input Multi-Output，MIMO）振动试验技术考虑了各个控制通道之间的相关性［4］，能够使得振动试验的应力分布更为合理［5］，并且还能为试验提供更高量级的推力［6］。因此，MIMO 振动试验技术越来越受到工程人员的关注。

目前，MIMO 随机振动试验主要集中于模拟宽带随机振动［7］，即根据试验要求，控制点处的功率谱密度（Power Spectral Density，PSD）分布于一个较宽的频率范围内［8］，常见的功率谱采用多段式的包络谱形式。考虑到实际振动环境的复杂性，有时由于结构（如桨叶、活塞、炮振等）产生的振动环境具有准周期激励特征，国军标［9］中推荐采用振源驻留振动的方式，即在宽带随机振动的背景上叠加高量级的窄带随机振动，该试验方式即是窄带加宽带随机振动。最新的美军标MILSTD-810H［10］中也对窄带加宽带（Random on Random，RoR）随机振动有相关规定。

目前，针对窄带加宽带随机振动试验的研究较少，特别是在MIMO 振动试验领域。张步云［11］结合时域随机化技术，将窄带与宽带相结合作为振动控制目标，实现了MIMO 窄带加宽带随机振动试验。但是该方法主要是基于高斯随机振动，而结构上的实测信号有时具有强的非高斯特征［12-14］，所以就工程意义而言，非高斯随机振动更受关注，当然实现的难度也更大。

Smallwood［15］利用零记忆非线性变换（Zero Memory Nonlinear Transform，ZMNL）方法将高斯信号转换成了非高斯信号，该方法计算原理简单，可以快速实现高斯随机信号向非高斯随机信号的转化，但是由于其同时对信号的幅值和相位进行调整，对于功率谱动态范围较大的随机信号会使其变换前后功率谱发生变化［16］。Steinwolf［17-18］根据相位与峭度的关系，提出了相位调节法生成非高斯随机信号，该方法仅对随机相位部分进行调整，因此不会对信号的功率谱产生影响。在国内，陈家焱［19］、吴家驹［20］、夏静［21］、朱大鹏［22］等均对非高斯随机振动进行了相关研究。

窄带加宽带非高斯随机混合振动试验中，由于窄带随机信号的能量在较窄的频率范围内要远大于宽带随机信号，所以常用的ZMNL 变换方法并不适用于RoR 非高斯随机振动环境试验。考虑到RoR 非高斯振动信号功率谱的动态范围特征，采用相位调节法生成非高斯信号更为合适，但是相位调节法需要逐次修正相位，使得信号慢慢逼近参考峭度。另外，除了用峭度来描述非高斯随机信号以外，常常还会考虑信号的偏度特征，所以如果同时考虑信号的偏度和峭度特征，必然降低了相位调节法生成非高斯随机信号的效率。

本文提出一种MIMO 窄带加宽带非高斯随机振动试验方式。首先，根据信号的偏度、峭度与随机相位的关系，提出了一种迭代修正的方法，使得信号的偏度和峭度可以快速逼近给定的偏度和峭度，提高相位调节法生成具有指定偏度和峭度非高斯随机信号的效率。然后，根据MIMO 振动中输入/输出的关系，采用时域逆系统方法实现驱动信号的生成。其次，对响应信号的PSD、偏度和峭度特性分别进行独立控制。最后，通过三轴振动台试验验证该方法的可行性。

1 基本理论

1.1 窄带加宽带信号特征

典型的窄带加宽带功率谱是在宽带功率谱的基础上叠加高量级的窄带随机信号，如图1 所示其中，f1和f6分别为宽带随机信号的起始和终止频率，f2和f5分别为宽带随机信号的拐点频率，f3和f4分别为各窄带随机信号的中心频率。可以看出，窄带随机信号的功率在中心频率附近要远远高于宽带随机信号，所以窄带加宽带随机信号功率谱的动态范围较大。因此，为使非高斯变换前后信号的功率谱保持不变，对非高斯变换算法有较高的要求。

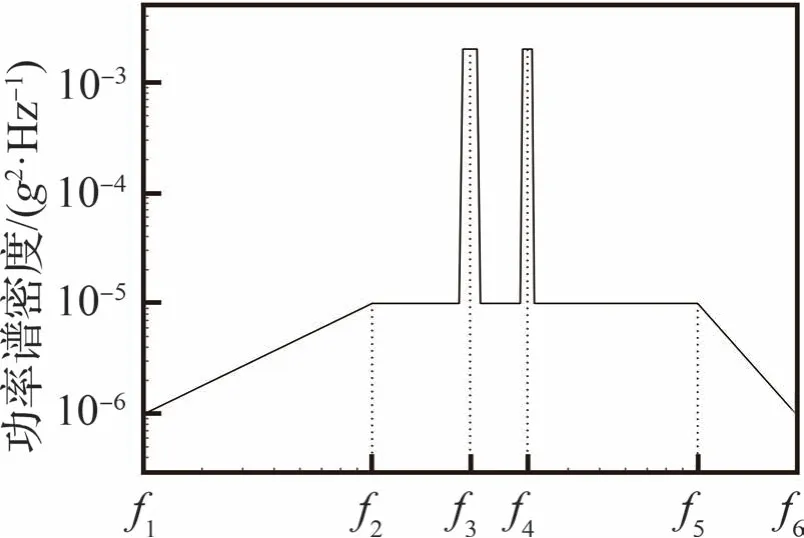
图1 窄带加宽带随机信号的功率谱Fig.1 PSD of narrowband on broadband random signal

1.2 相位调节法

功率谱密度可以用来描述平稳随机信号在频域中的功率分布，由于功率谱仅与傅里叶谱的幅值有关，所以相位调节法不会影响信号的功率谱。假设某随机信号的功率谱有N根谱线，则该随机信号对应的偏度S和峭度K可以写为

式中：A为信号各谱线对应的幅值，φ为随机相位。

对于高斯随机信号，相位角φ是均匀分布在［-π，π］内，使得余弦函数值均匀分布在［-1，1］范围内，通过随机值的相互补偿，使得式（1）和式（2）中带三角函数项的总和趋于0，从而呈现出高斯特征。对于非高斯随机信号，通过调节φ的值可以使得余弦函数值的分布发生变化，以i+2j=k项为例，常用的方法可以通过调节多组相位角，使其满足φi+2φj-φk=0，从而增大信号的峭度，直至其逼近给定的参考。另一方面，由于相位调节法仅使得随机相位发生变化，信号的幅值不参与调节，所以不会改变随机信号的功率谱，相较于ZMNL 变换，相位调节法在窄带加宽带非高斯随机振动中更适用。

1.3 非高斯特征与随机相位的关系

调节随机相位角对应的三角函数关系，虽然可以使得峭度发生变化，但是这种调节方式必然是费时的。另外，偏度和峭度的调节还有可能会相互影响，因为两者共用同一组随机相位。通过观察可以发现，当式（1）和式（2）中所有的相位全部为零时，信号的偏度和峭度将达到最大Smax和Kmax，此时的最大值仅与功率谱的幅值大小有关。另一方面，既然随机相位分布在［-π，π］内，可以使得信号的偏度趋于0 且峭度趋于3，那么如果改变随机相位的分布范围肯定也能改变信号的偏度和峭度。

定义参数a和b（0＜a＜1， -1＜b＜1）来控制随机相位的取值范围，a控制取值宽度，b控制取值位置。所以，当随机相位的分布范围变为［-aπ+bπ，aπ+bπ］时，可以得出当b为一定值时，信号的偏度、峭度与a的关系如图2 所示。可以看出，当b为一定值时，偏度和峭度与a成反比，即随机相位取值区间的宽度会同时影响非高斯随机信号的偏度和峭度，但是当a增大到1 附近时，偏度趋于0 且峭度趋于3，这是因为随机相位均匀分布在2π 的宽度范围内时会使得随机信号呈现出高斯分布特征。另外，当a为一定值时，信号的偏度、峭度与b的关系如图3 所示。当a为一定值时，偏度和峭度会随着随机相位的取值位置发生变化，并且偏度和峭度在-1＜b＜1 范围内呈现出对称的特征。

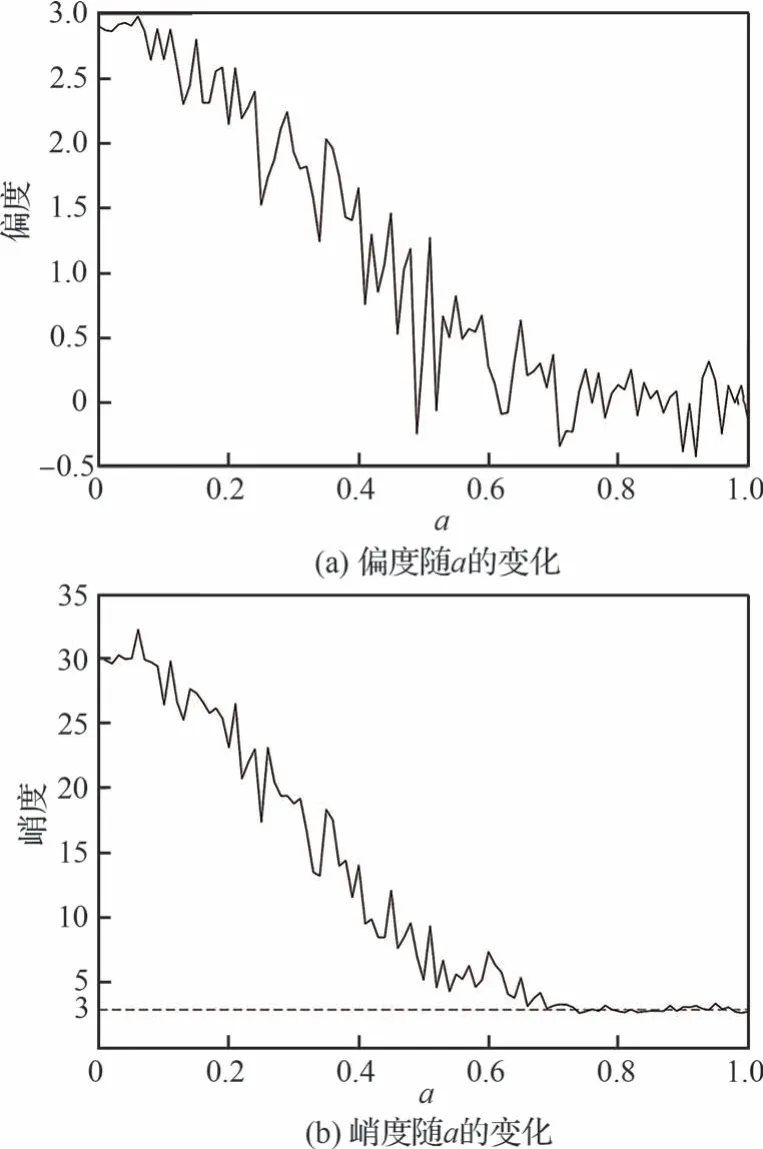
图2 偏度、峭度随a 的变化关系（b=0.2）Fig.2 Variations of skewness and kurtosis with a for b=0.2

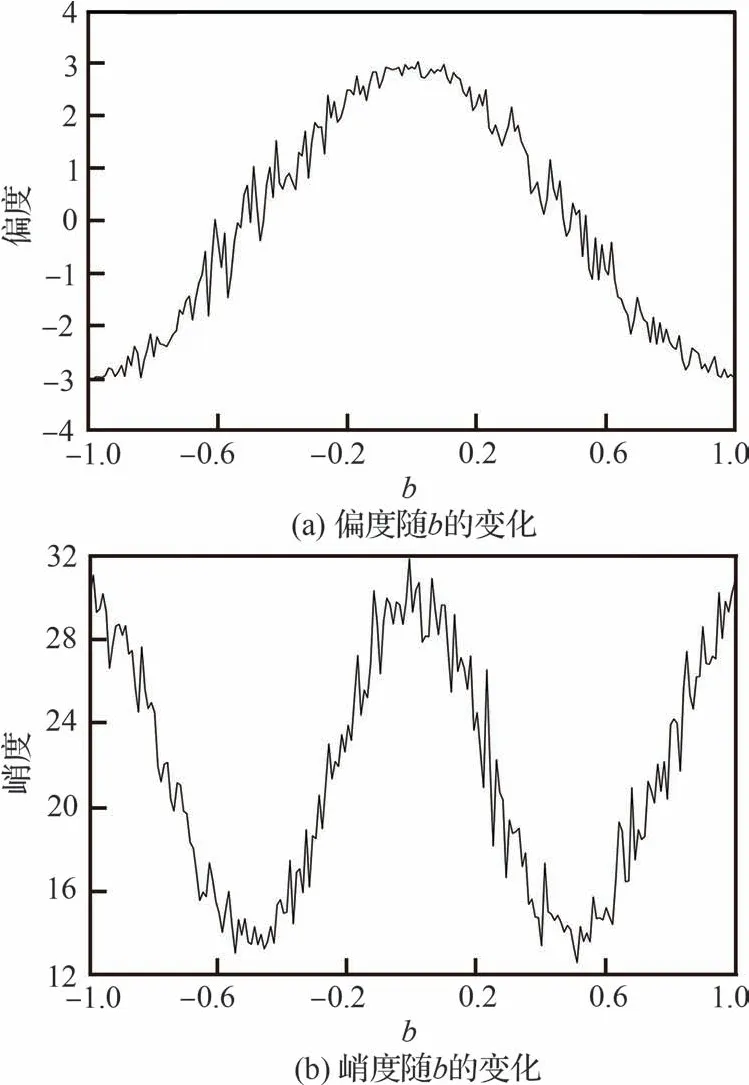
图3 偏度、峭度随b 的变化关系（a=0.2）Fig.3 Variations of skewness and kurtosis with b for a=0.2

既然a和b的变化可以同时带来偏度和峭度的改变，因此本节提出采用调节参数a和b的方式迭代计算随机相位，使非高斯随机信号的偏度和峭度满足参考值。

首先，令所有谱线的相位角为零，得到最大偏度Smax和最大峭度Kmax；然后反复迭代修正a和b的大小，最终使得偏度、峭度与参考偏度和峭度之差在给定的误差范围内，迭代公式如下

式中：Sr和Kr分别为参考偏度和参考峭度，S和K分为本次迭代时生成的非高斯随机信号的偏度和峭度。aold和anew以及bold和bnew分别为本次迭代和下一次迭代时采用的参数a和b。

采用本节提出的迭代方法生成偏度为0.2、峭度为6 的非高斯随机信号的时域片段和功率谱密度如图4 所示。可以看出由于仅调节随机相位的值，并不会改变信号的功率谱，所以相位调节法生成非高斯随机信号的功率谱可以与参考谱贴合。而采用ZMNL 变换生成非高斯随机信号的功率谱，受信号动态范围的影响，使得变换以后功率谱发生了较大的变化，无法用于窄带加宽带的非高斯随机信号生成。

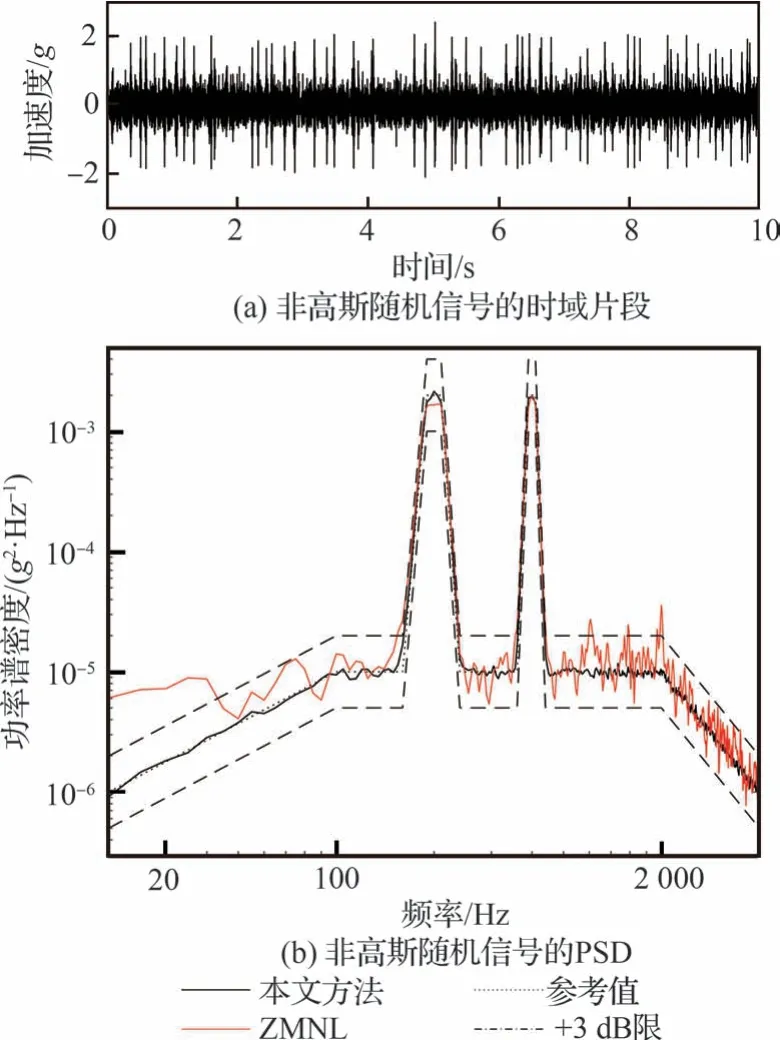
图4 迭代法生成窄带加宽带非高斯随机信号Fig.4 Generation of RoR non-Gaussian random signal by iteration method

当随机相位全部为0 时（即a=0 且b=0），所得非高斯随机信号的偏度和峭度最大，虽然此时生成信号的功率谱密度仍然满足给定参考谱要求，但是时域信号更多表现以高量级的窄带信号叠加高量级的冲击信号为主，其他的宽带随机信号则近似于小量级的噪声，即合成的信号发生了“畸变”，如图5 所示。因此，为避免发生这种“畸变”现象，本文推荐偏度和峭度的取值范围分别为

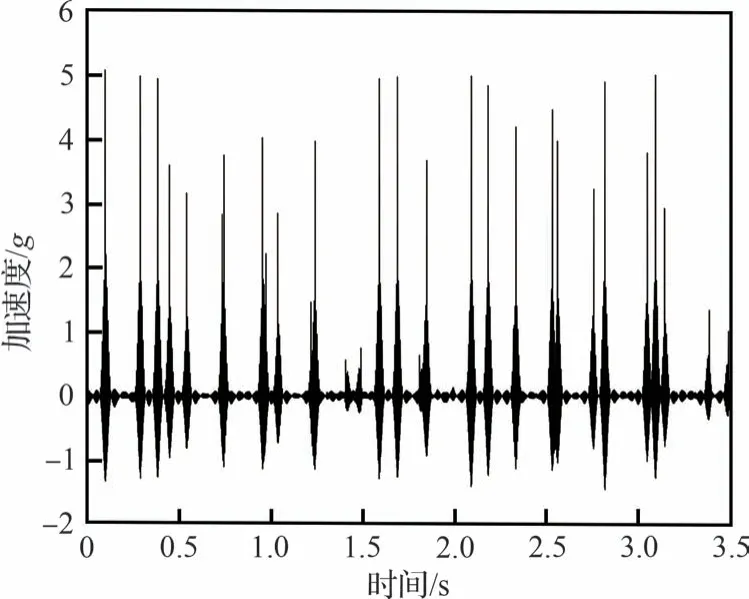
图5 生成的非高斯随机信号（ a = b = 0）Fig.5 Generated non-Gaussian random signal（ a = b = 0）

1.4 MIMO 驱动信号生成

MIMO 窄带加宽带非高斯随机振动的目标是使得控制点处的功率谱与给定的参考谱相匹配。考虑到多通道之间的耦合作用，本节提出采用时域逆系统方法来生成驱动信号。

对于n点激励n点响应（n≥2）的线性时不变系统，信号的参考谱在频域中可以写为

式中：ri（ii= 1，2，…，n）为第i个点的自功率谱，rij为第i个控制点和第j个控制点之间的互功率谱。

利用Cholesky 分解可以将R分解为下三角矩阵，即

式中：上标“H”表示复共轭转置。

通过对分解以后的L矩阵添加随机相位，再利用时域随机化算法，可以生成同时满足参考偏度、参考峭度、自功率谱和互功率谱的时域非高斯随机信号（yt）。

以两输入两输出为例进行说明，针对多输入多输出情况可以以此类推。由于功率谱R缺少相位信息，时域随机化算法需要为矩阵L添加随机相位，即

式中：P为仅包含对角线元数的随机相位矩阵，j2=-1。

利用1.3 节中所述方法调节Y（1，1）中随机相位φ1的取值范围可以得到第1 个输出通道中的非高斯随机信号。然后调节Y（2，2）中随机相位φ2的取值范围可以得到第2 个输出通道中的非高斯随机信号。同时还可以注意到φ1和φ2的调节是相互独立的，也就是说Y（2，2）中随机相位的调节不会影响Y（2，1）的取值，Y（2，1）的取值仅与Y（1，1）中的相位角有关，所以分别调节Y（1，1）和Y（2，2）中的随机相位不会对最终各通道之间随机信号的互谱产生影响，从而实现各个通道之间相位调节的解耦。

需注意的是，式（9）中的L和P中均有涉及相位。但是L中的相位表示的是2 个不同控制点之间的相位差，即互谱关系。P中的相位是因为功率谱R中的自谱缺少相位信息而添加的随机相位。本文所提出的迭代相位调节法是针对随机矩阵P进行调节，而生成非高斯随机信号。由于矩阵P仅包含对角线元素，所以式（8）和式（9）仍然具有关系：

所以对矩阵P中相位的调节并不改变矩阵L中的相位，即不会对控制点之间的相位差产生影响。

对矩阵Y进行时域随机化处理即可得到时域非高斯随机信号y（t）。然后，以y（t）作为控制信号，将原问题转换成求系统输入的逆问题，因此驱动信号可以写为

式中：d（t）为各通道的驱动信号；H为系统传递矩阵，可表示为

其中：h为单位脉冲响应函数矩阵，可以通过频响函数的逆傅里叶变换获得［23］。

1.5 控制算法

为保证最终控制信号的功率谱、偏度和峭度满足给定的参考值，还需要引入控制算法调整输入信号分别对响应的功率谱、偏度和峭度进行控制。

对功率谱的控制采用幂次控制算法，具体表示为

式中：ε为收敛因子。用L（m+1）代替式（9）中的L矩阵用来生成新的驱动信号d（t）。误差矩阵Δ为

其中：Lr为参考谱矩阵R的Cholesky 分解的下三角矩阵；Ly为响应信号功率谱矩阵Cholesky 分解的下三角矩阵。

对第i（i=1，2，…，n）个通道信号偏度和峭度的修正表示为

式中：ηs和ηk分别为偏度和峭度的收敛系数。上标m+1 和m分别为第m+1 次和第m次迭代修正时对应的值。误差参数Δs和Δk为

其中：Sr和Sy分别为参考偏度和响应的偏度；Kr和Ky分别为参考峭度和响应的峭度。

MIMO 窄带加宽带非高斯随机振动试验的具体流程如图6 所示。

图6 MIMO 窄带加宽带非高斯随机振动试验流程图Fig.6 Flow chart of control method for MIMO RoR non-Gaussian random vibration test

2 试 验

为验证提出的MIMO 窄带加宽带非高斯随机振动试验方法的工程可行性，采用三轴向振动台进行试验验证。振动试验系统如图7 所示，控制点1 和2 处的加速度传感器分别对应振动台台面的x和y方向的加速度响应，VXI 数采系统和计算机用于采集、发送和处理信号。试验频率范围为20 ～2 000 Hz，谱线数400 线。自功率谱控制容差设置为±3 dB 报警限和±6 dB 停机限，互谱不设限。2 个控制点间的相干系数设为0.6，相位角设为60°。控制点1 和2 的参考峭度分别为6和5，控制点1 的参考偏度设为0.2，控制点2 的参考偏度设为0。

图7 振动试验系统Fig.7 Vibration test system

未进行控制时，x和y方向的自功率谱、相干系数和相位如图8 所示。可以看出未控制时，x和y方向上的自功率谱均有超出±3 dB 报警限的谱线，因此还需要采用控制算法对其进行修正。

图8 x 和y 方向未控制的自功率谱、相干系数和相位Fig.8 Uncontrolled PSD， coherence and phase at x and y directions

修正后x和y方向上的自功率谱、相干系数和相位如图9 所示。可以看出，2 个方向上的自功率谱均控制在±3 dB 报警限内，满足给定的参考要求。相比未控制时的情况，信号高频处的相干系数和相位也有所改善。

图9 修正后x 和y 方向的自功率谱、相干系数和相位Fig.9 Controlled PSD， coherence and phase at x and y directions

2 个方向上的偏度和峭度控制如图10 所示，可以看出信号的偏度和峭度经过迭代修正以后被稳定在了参考值附近。x和y方向上的时域加速度信号片段如图11 所示，可以看出，时域信号呈现出明显的非高斯特征。

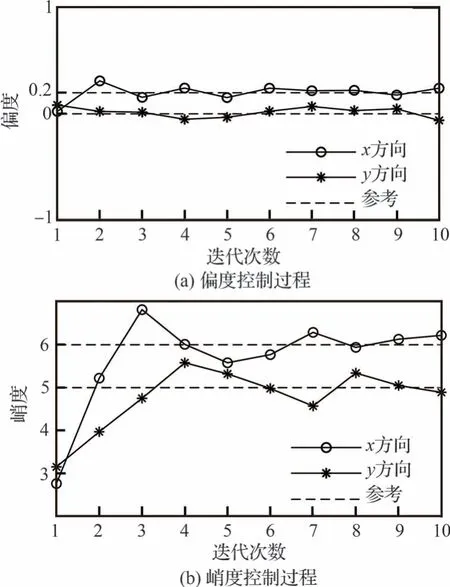
图10 x 和y 方向上的偏度和峭度控制Fig.10 Skewness and kurtosis control at x and y directions

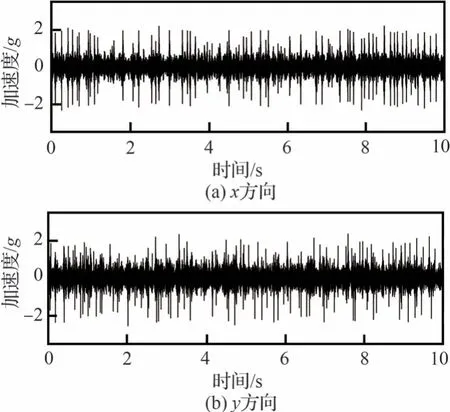
图11 x 和y 方向上的时域加速度响应片段Fig.11 Segment of acceleration response at x and y directions in time domain

x和y方向上参数a和b的迭代取值如图12所示。可以看出，当非高斯随机信号的偏度和峭度稳定在参考值附近时，参数a和b的取值也随之稳定。

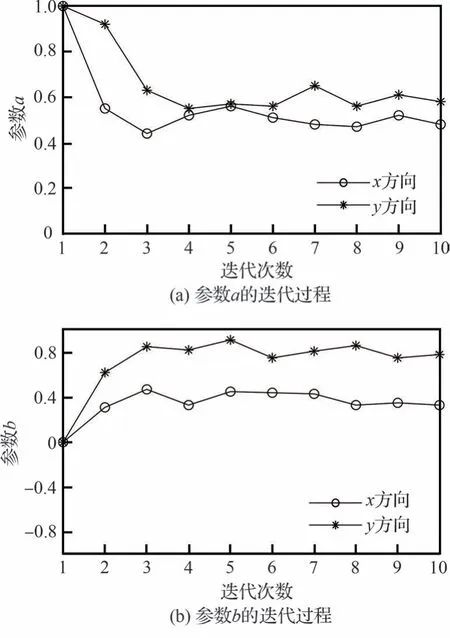
图12 参数a 和b 的迭代过程Fig.12 Iteration process of parameters a and b

3 结 论

1） 非高斯信号的偏度和峭度与随机相位的取值范围和取值位置有关，采用本文提出的迭代相位调节法可以快速生成具有指定偏度和峭度的非高斯随机信号，并且该方法生成的非高斯随机信号不会对信号的功率谱产生影响。

2） 本文通过时域逆系统方法生成的驱动信号可以实现各个通道之间相位调节的解耦，各通道上随机相位的调节不会相互影响，从而不会影响最终生成各通道之间非高斯随机信号的相干系数和相位。

3） 通过三轴向振动台试验验证了本文所提方法的理论可行性和工程有效性。该方法能同时实现对自功率谱、互功率谱、偏度和峭度的控制，可为工程应用提供参考。