基于时空轨迹信息的目标行为模式在线分类方法

姜乔文，刘瑜，丁自然，孙顺，简涛

海军航空大学 信息融合研究所，烟台 264001

在预警监视领域，随着卫星、雷达、ADS-B（Automatic Dependent Surveillance-Broadcast）、AIS（Automatic Identification System）、声呐以及高清摄像机等目标探测技术的快速发展，覆盖天基、空基、岸基、海上甚至水下的多层次预警监测体系已经基本形成［1-3］。监视场景下的运动目标得到了清晰准确的检测、跟踪和关联，形成不断更新的目标时空信息，最终以时空轨迹的形式记录下来。海量的时空轨迹数据在航空电子系统等目标信息处理中心不断存储和积累，其中隐含着大量规律性的信息和知识。基于数据挖掘中的聚类技术可以从海量的历史数据中挖掘出目标的频繁行为模式［4-6］，但离线的数据分析不具备时效性，难以适用于态势实时更新的预警监视场景。在预警监视系统中，实时地对未知身份目标的时空轨迹行为进行预测和判定是实现态势感知的有效途径。当前，行为判定多以人工处理方式为主，这不仅要求情报处理人员具备大量的先验知识，同时消耗大量的时间和精力，效率低且准确性差。因此，如何实现系统智能化在线分析目标行为是当下预警监视领域亟待解决的问题，这对于提升信息处理效率、及时分析和预测目标行为意图、辅助指挥员决策部署以及实现智能化态势感知具有重要的现实意义。

近年来，国内外科研人员在目标行为模式分类方面开展了大量的研究工作［7-11］。赵竹珺和吉根林［12］对时空轨迹分类研究进展进行了详细的总结，针对现有的轨迹分类算法的特点，从数据来源、分类器、特征提取方式等方面进行了对比分析，并对设计增量式学习算法建立轨迹分类器提出了展望。潘新龙等［13］针对预警监视和指挥决策需求，对现有的目标行为模式在线分类技术进行了总结与展望。曹卫权等［14］基于运动目标的区域分布，采用核密度估计和最大似然判决的方法对轨迹段进行分类。崔彤彤等［15］结合卷积神经网络和长短期记忆网络优势学习船舶AIS轨迹特征，实现了船舶轨迹和类型的分类。Owens 和Hunter［16］针对视频监控系统中检测到的目标行为自动分类问题，采用自组织映射神经网络对正常的轨迹特征进行学习，实现无模型轨迹分类和异常检测。Bolbol 等［17］基于支持向量机构建分类推理框架，来解决GPS 数据在不同交通方式（汽车、步行、自行车、地铁、火车和公共汽车）中的分类问题。Saini 等［18］采用粒子群算法融合轨迹的全局和局部特征，并基于图方法对轨迹进行分类。Pan 等［19］采用多因素Hausdorff 作为轨迹相似性度量，通过构造一致性多类分类器对预警监视区域的频繁行为模式进行在线分类。

虽然目前轨迹分类领域已有大量的研究，但现有方法依然存在以下几点局限性：场景设置理想化，没有考虑到离群轨迹对在线分类器的影响；分类模型复杂，导致时间消耗大，实时性有待提升；仅从空间位置信息度量轨迹相似性，忽略了航向和速度等特征。

本文针对上述轨迹分类方法的几点局限性展开，主要贡献如下：① 提出了归纳式一致性多类预测器（Inductive Conformal Multi-class Predictor， ICMP），兼顾分类和离群样本检测功能，并提高了训练和在线检测的效率；② 提出了时空Hausdorff 距离（Spatio-Temporal Hausdorff Distance， STHD）和定向时空Hausdorff 最近邻不一致性度量函数（Directed Spatiotemporal Hausdorff Nearest Neighbor Nonconformity Measure， DSHNN-NCM），可以有效区分空间位置相似但运动速度和方向不同的轨迹；③ 提出了序贯时空Hausdorff 最近邻归纳式一致性多类预测器（Sequential Spatiotemporal Hausdorff Nearest Neighbor Inductive Conformal Multi-class Predictor， SSHNN-ICMP），对预警监视场景下目标频繁出现的行为进行在线学习和预测；④ 通过仿真和实测数据实验证明了算法在目标行为在线分类准确性和实时性上的优势。

1 一致性预测

1.1 一致性多分类器

一致性预测［20-21］（Conformal Predictor，CP）（算法1）是一种基于Kolmogorov 随机性理论转导推理的域预测机器学习算法，该算法的前提是假设样本是独立和同分布的。首先在对测试样本进行预测之前设定一个置信水平，然后对训练样本集和待测样本序列进行随机性检验，通过不一致性度量函数（Nonconformity Measure，NCM）计算待测样本序列与训练样本集不一致程度的定量估计，最后将所有随机性检验值超过置信水平的所有类别标签作为域预测的结果。一致性预测算法的预测风险可控，但是预测结果可能不唯一。为了保证预测过程对每个测试样本的独立性，一致性预测过程采用在线学习方法，对于不同的测试样本，训练样本集不断更新。对于第k+1 个测试数据，前k个测试样本已经被添加到训练样本集中，以此来在线扩展训练样本集。

算法1 一致性预测（CP）算法输入：训练数据集{z1，z2，…，zl}，测试数据xl+1，不一致性度量函数A，置信水平ε输出： 对测试数据xl+1 的预测标签集合yεl+1 01.yεl+1 ←∅02.for all y ∈{1，2，…，c}03.zl+1 ←(xl+1，y)04.for i ←1 to l+1 do 05. αi ←A({z1，z2，…，zl+1}zi，zi)06. end for 07. p ←|{i ∈{1，2，…，l l，+l+1 1 }|αi ≥αl+1}|08. if p ＞ε then 09. yεl+1 ←yεl+1 ∪{y}10. end if 11.end for 12.{z1，z2，…，zl}←{z1，z2，…，zl}∪xl+1

在给定的置信水平ε的前提下，一致性预测器能够预测可控风险下的类别。然而，对于同一个测试样本，一致性多分类器可能得到几个不同的类别标签；除此之外，ε的取值对一致性预测结果至关重要，在很多应用中选择合适的ε值是非常困难的，需要通过专家经验来尝试，不具有鲁棒性，这在预警监视应用中是不能接受的。为了解决上述问题，Pan 等［19］提出了一致性多类分类器（Conformal Multi-class Classifier， CMC）（算法2）。该分类器可以保证预测的唯一性，而且在分类时不需要ε，解决了ε取值困难的问题，具有较强的鲁棒性。

算法2 一致性多类分类器（CMC）算法输入：训练数据集{z1，z2，…，zl（}按类别标签分为c 个子集{z1，z2，…，zl1}，…，{z1，z2，…，zlc}，l1+l2+…+lc=l），测试数据zl+1，不一致性度量函数A输出： 对测试数据zl+1 的预测标签yl+1 01.for all y ∈{1，2，…，c} do 02.zl+1 ←(xl+1，y)03.for i ←1 to ly 04. αyi ←A({z1，z2，…，zly，zl+1}zi，zi)05.end for 06.αl+1 ←A({z1，z1，…，zly}，zl+1)|||||{i ∈{1，2，…，ly，l+1 }|αyi ≥αl+1}|||||07.pyl+1 ←ly+1 08.end for 09.pcl l+ass1 ←max{p1l+1，p2l+1，…，pcl+1}，class ∈{1，2，…，c}10.yl+1 ←class 11.{z1，z2，…，zlclass}←{z1，z2，…，zlclass，zl+1}

1.2 带有离群检测的归纳式一致性多分类预测器

CMC 作为一种在线预测器，最突出的问题是在线计算的效率。在计算测试样本集中每个样本的不一致性度量值时，CMC 需要反复访问和存储样本的相似度度量矩阵，耗时较长，因此仅适用于数据规模较小和低实时性要求的应用。除此之外，在实际预警监视场景中，目标的行为并不是都遵循已知的行为模式，会不断出现无规则的离群轨迹。当采用CMC 对目标行为进行预测时，不论在哪一类型为模式中，离群轨迹经过不一致性度量会得到一个很小的p值，由于算法未对p值进行有效限制，从而导致将离群轨迹强行预测为某一种行为模式，这在预警监视应用中是不能接受的。针对上述问题，结合归纳式一致性 预 测［22］（Inductive Conformal Predictor，ICP） 和一致性异常检测［23］（Conformal Anomaly Detector， CAD）的思想，提出了带有离群检测的归纳式一致性多分类预测器（Inductive Conformal Multi-class Predictor with outlier detector， ICMP）（ 算法3）。

算法3 ICMP 算法输入：训练数据集{z1，z2，…，zl（}按类别标签分为c 个子集{z1，z2，…，zl1}，…，{z1，z2，…，zlc}，l1+l2+…+lc=l，每个子集分为压缩样本集{z1，z2，…，zu1}，…，{z1，z2，…，zuc}和检验样本集{zu1+1，zu1+2，…，zl1}，…，{zuc+1，zuc+2，…，zlc}），不一致性度量函数A，风险水平ε 训练集{z1，z2，…，zl（}分为压缩样本集{z1，z2，…，zu}和检验样本集{zu+1，zu+2，…，zl}），测试数据zl+1，不一致性度量函数A，风险水平ε输出： 对测试数据zl+1 的预测标签yl+1 01.for all y ∈{1，2，…，c} do 02.for i ←uy+1 to ly 03. αyi ←A({z1，z2，…，zuy}，zi)04. end for 05.end for 06.for all y ∈{1，2，…，c} do 07.zl+1 ←(xl+1，y)09. αl+1 ←A({z1，z2，…，zuy}，zl+1)|||||{i ∈{uy+1，uy+2，…，ly，l+1 }|αyi ≥αl+1}|||||10.pyl+1 ←ly-uy+1 11.end for 12.pcll+ass1 ←max{p1l+1，p2l+1，…，pcl+1}，class ∈{1，2，…，c}13. if pcl l+ass1 ＜ε then 14. yl+1 ←0（Outlier）15.else 16. yl+1 ←class 17.{z1，z2，…，zlclass}←{z1，z2，…，zlclass，zl+1}

第一，针对在线计算效率的问题，基于归纳式一致性预测的思想来改善一致性多分类器的在线学习的实时性。将每一类训练样本集{z1，z2，…，zl1}，…，{z1，z2，…，zlq}，…，{z1，z2，…，zlc}划 分 为 压 缩 样 本 集{z1，z2，…，zu1}，… ，{z1，z2，…，zuq}，…，{z1，z2，…，zuc}和检验样本集{zu1+1，zu1+2，…，zl1}，…，{zuq+1，zuq+2，…，zlq}，…，{zuc+1，zuc+2，…，zlc}。压缩样本集是一个固定的集合，用来学习构建一个规则模型，不随检测样本的更新而改变；只有检验样本集随检测样本的更新而改变，这样既可以实时更新测试数据，又保证了计算效率。检验样本集中样本的不一致性度量值通过压缩样本集计算，对于第q类检验样本集{zuq+1，zuq+2，…，zlq}中的样本，其不一致性度量值

对于测试样本zl+1，其不一致性度量值

每一类样本中随机性检验值的估计为

为了证明ICMP 在计算效率上的优势，分析ICMP 和CMC 对其不一致性度量算法A的复杂度。当A应用于一个包含l个训练数据和s个测试数据的数据集时，算法的整体复杂度可以表示为

式中：Atrain(l)表示A生成其通用规则所需的时间；Aapply表示将该通用规则应用到一个新测试数据所需的时间［22］。CMC 每完成一个测试样本后都需要更新训练样本集，且不一致性度量值在每次测试时也需要不断更新，其复杂度表示为

式中：c表示类别数；lq表示第q类训练样本集的样本个数。而ICMP 通过固定的压缩样本集归纳得到检验样本集和测试样本的不一致性度量值，而且只需要训练一次，不需要随着测试样本的更新而改变，其复杂度为

因此，当测试样本规模很大时，ICMP 计算效率要远优于CMC。

第二，针对一致性多分类器对离群样本不敏感的问题，基于一致性异常检测的思想，对算法增加了风险评估。首先设定一个风险水平ε，当最终的随机性检验值确定后，将其与风险水平ε比较。当＜ε时，则把测试样本zl+1判定为离群样本；当时，则对测试样本zl+1进行正常的分类预测。这样就很好地避免了离群轨迹对目标行为分类准确性的影响。

2 不一致性度量函数

2.1 时空Hausdorff 距离

时空轨迹数据是由若干个目标位置信息按时间顺序构成的序列。在一段时间内预警监视系统中积累目标的所有时空轨迹集合表示为

式中：TR 表示时空轨迹数据集合；i为轨迹编号；n为轨迹总数；tri表示数据集中的第i条时空轨迹，即

其中：pi，k表示第i条轨迹中的第k个时空信息数据点；m表示轨迹tri中时空信息点总数，通常情况下，不同轨迹的时空信息点总数m不尽相同。

pi，k是一个包含目标时间和空间位置信息的向量，pi，k=[ti，k，li，k]。其中时间信息用ti，k表示，满足ti，k＜ti，k+1；空间位置信息用li，k表示，li，k既可以是二维空间中的位置点(xi，k，yi，k)，也可以是三维空间中的位置点(xi，k，yi，k，zi，k)。

Hausdorff 距离［24-25］（Hausdorff Distance，HD）是一种广泛应用的轨迹相似性度量方法，它的优点在于可以度量整条轨迹的全局特征，当轨迹不完整时依然可以很好地进行相似性度量。传统的轨迹Hausdorff 距离度量基于轨迹的空间位置信息，对于2 条轨迹tri和trj，定向Hausdorff距离的意义为轨迹tri中的位置信息点到trj中的位置信息点的最近距离中的最大值，表示为

式中：dist(li，k，lj，k)表示两点之间的欧氏距离。在二维空间中，

在三维空间中，

传统的轨迹相似性度量方法，如欧氏距离［26］、DTW［27］、Hausdorff 距离等，都是基于目标运动空间中的位置信息，未能有效地将目标的位置、速度、航向等多维特征信息进行融合，因此很难区分位置相近而运动特征存在较大差异的目标轨迹。而事实上，目标在运动过程中的位置信息是目标的速度、航向等特征在时间上积累的结果，尽管在空间维度中位置相近，但在时间维度上，运动特征不同的轨迹却有着很高的区分度。因此，我们在目标运动空间的基础上引入时间维度，在时空域中基于Hausdorff 距离度量轨迹的相似性，提出了时空Hausdorff 距离（Spatio-Temporal Hausdorff Distance， STHD） 。

在时空域中，空间维中的量纲是距离单位，时间维中的量纲是时间单位，两者量纲的不同导致无法直接利用欧氏距离进行度量。考虑到距离的量纲与时间的量纲之间相差一个速度量纲，因此只需要在时间维度上乘上一个具有速度量纲的参量即可。设定该参量为整个数据集中目标运动的平均速度

式中：count(pi，k)表示轨迹tri中信息点的总数。

于是tri中每个轨迹信息点在时空域中的坐标就可以表示为

其中，式（13）用来表示二维空间中的运动目标，式（14）用来表示三维空间中的运动目标。

然后，在时空域中定义轨迹tri和trj之间的定向时空Hausdorff 距离为

定向时空Hausdorff 距离也不具备对称性，因此定义两者的较大值为时空Hausdorff 距离

如图1 所示，尽管在空间维度上3 个运动速度和航向相异的目标轨迹Hausdorff 距离相近，但是在时空域中，可以准确地将运动特征不同的目标轨迹区分开。

图1 STHD 示意图Fig.1 Schematic diagram of STHD

2.2 时空Hausdorff 最近邻不一致性度量函数

不一致性度量函数（Nonconformity Measure， NCM）是一致性预测算法的一个重要组成部分，用来计算待测样本序列与训练样本集不一致程度的定量估计。不一致性度量函数的构造通常基于机器学习的分类算法，其中应用最广泛的是K 近邻算法［24］

式中：表示测试样本zi到与它同类别训练样本中第j近的距离；表示测试样本zi到与它不同类别训练样本中第j近的距离。该定义假设具有相同标签的样本彼此很接近，而具有不同标签的样本彼此距离较远。

由于ICMP 本质上还是一种多类分类器，因此并不需要考虑到其他类的距离。为了描述时空维度中目标轨迹的不一致性，我们结合STHD和K 最近邻（K Nearest Neighbor， KNN）的思想，提出了定向时空Hausdorff 最近邻不一致性度量函数（Directed Spatiotemporal Hausdorff Nearest Neighbor Nonconformity Measure，DSHNN-NCM）

式中：{tri，tri+1，…，trn}表示目标时空轨迹组成的压缩样本集；N (tri，{tri，tri+1，…，trn} ri，K)表示时空轨迹tri到与它同类别训练样本中定向时空Hausdorff 距离第K近的时空轨迹。在预警监视场景的应用中，K的值通常可以取2、3、4 或5。

3 目标行为模式在线预测方法

基于1.2 节提出的ICMP 和2.2 节提出的DSHNN-NCM，提出了带有离群检测的序贯时空Hausdorff 最近邻归纳式一致性多类预测器（Sequential Spatiotemporal Hausdorff Nearest Neighbor Inductive Conformal Multi-class Predictor with outlier detector， SSHNN-ICMP），用于对预警监视场景下目标频繁出现的行为模式进行在线学习和预测，主要流程如图2 所示，具体实现步骤（算法4）如下：

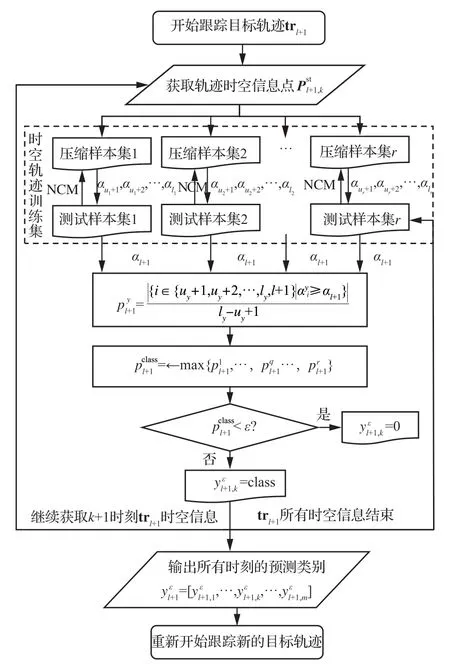
图2 SSHNN-ICMP 流程图Fig.2 Flow chart of SSHNN-ICMP

输入

2） 测试轨迹trl+1，以按时间顺序输入的时空信息点更新trl+1，m为时空轨迹长度。

3） 最近邻参数K。

4） 风险水平ε。

算法4 SSHNN-ICMP输入 训练集C1，C2，…，C（r分为压缩样本集C1c，C2c，…，Crc 和检验样本集C1t，C2t，…，Crt），测试轨迹trl+1，最近邻参数K，时空Hausdorff 距离向量μ1，μ2，…，μr，零向量h1，h2，…，hr，Q 风险水平ε输出 更新所有pslt+1，k 后轨迹trl+1 的预测行为标签集yεl+1 01.for k ←1 to m do 02.for all y ∈{1，2，…，r} do 03. for i ←uy+1 to ly do 04. αyi ←μiy-uy 05. end for 06. for g ←1 to uy do 07. hqg ←max{hst( pslt+1，k，trg)，hqg}08. if g ≤K then 09. Q.insertElement(hqg)10. else if Q.maxElement()＞hqg then 11. Q.removeMaxElement()12. Q.insertElement(hqg)13. end if 14. end if 15. end for 16. αl+1 ←Q.maxElement()17. Q.removeAllElements()|||||{i ∈{uy+1，uy+2，…，ly，l+1 }|αyi ≥αl+1}|||||18.pyl+1 ←ly-uy+1 19.end for 20.pcll+ass1 ←max{p1l+1，…，pql+1，…，prl+1}21.if pcl l+ass1 ＜ε then 22. ylε+1，k ←0 23.else 24. yl ε+1，k ←class 25.end for 26.yεl+1 ←{ylε+1，1，…，ylε+1，k，…，ylε+1，m}27.Cy tl ε+1，m ←Cy tl ε+1，m ∪trl+1 28.Update μ1，…，μq，…，μr

5） 时空Hausdorff 距离向量μ1，…，μq…，μr，其中μq是一个维度为(lq-uq)×1 的列向量，μiq表示第q类行为模式检验样本集中第i条轨迹到压缩样本集轨迹中第K近的时空Hausdorff距离。

6） 零向量h1，…，hq，…，hr，其中hq是一个维度为uq×1 的列向量。

7） 空排序集Q。

输出

每更新一个时空信息点pl+1，k后轨迹trl+1的预测行为标签集其中表示离群轨迹。

1.2.2 各间隙调整正确。如秧针与导轨插口侧面的标准间隙为1.3～1.7 mm，秧针和苗箱侧面的标准间隙为1.5～2.5 mm。

步骤1对于轨迹trl+1在tk时刻更新的时空信息点，首先在第1 类行为模式的训练集C1重复如下操作：

1） 通过时空Hausdorff 距离向量μ1计算检验样本集中所有轨迹相对于压缩样本集的不一致性度量值

2） 计算更新的时空信息点相对于压缩样本集中所有轨迹的有向Hausdorff 距离并与前一个时刻进行比较，取两者中的较大值作为该时刻轨迹trl+1子轨迹相对于压缩样本集中所有轨迹的有向时空Hausdorff距离

3） 更新空集Q，当Q中的元素个数超过K时，将所有的存入Q中；当g＞K时，将当前的与Q中的最大值相比，若小于Q中的最大值，则将Q中最大的元素剔除，并将插入到Q中。

4）Q中最大的元素即为该时刻trl+1子轨迹相对于压缩样本集中所有轨迹的K 最近邻时空Hausdorff 距离，由此计算轨迹trl+1子轨迹的不一致性度量值

之后清空Q中所有元素。

5） 计算的值

步骤2在剩余r-1 类的训练集Cq中重复步骤1）～4）操作，计算得到

步骤3取中的最大值作为trl+1子轨迹在该时刻的一致性检验值

步骤4判断trl+1子轨迹在该时刻的一致性检验值pl+1与风险水平ε的大小关系。若pl+1＜ε，则判定轨迹trl+1为离群轨迹；若pl+1≥ε，则将trl+1子轨迹在该时刻的行为分类为中最大值所对应的行为模式。

步骤5持续对更新后的trl+1子轨迹进行行为判定，直到时空信息点不再更新。获取trl+1整条轨迹在跟踪过程中的行为模式标签集

步骤6将存入相应类别的行为模式训练集的检验样本集中，并更新相应的时空Hausdorff距离向量。

4 仿真数据验证分析

本实验模拟了某预警监视区域中未知飞行器的10 种飞行行为，生成了含有10 种类别标签的时空轨迹，我们在该数据集上实现了SSHNNICMP 算法，研究了算法的性能，并对实验结果进行详细的分析和讨论。

4.1 仿真轨迹数据集

本节的时空轨迹数据集由Piciarelli 等［28］公开发表的轨迹模拟程序生成，可以模拟产生带有类别标签的规律性轨迹以及随机的异常航迹。

用该程序产生二维空间中的目标轨迹数据，并人为添加信息数据点中目标的时间信息。该数据集共包含1 600 条时空轨迹，其中包括1 500 条规律性轨迹和100 条无规律轨迹，所有轨迹如图3所示。规律性轨迹包含10 种行为模式，标签1～3的行为模式在同一位置生成，以行为1 为参照，行为2 速度是行为1 的2 倍，行为3 与行为1 运动方向相反，每种行为有150 条轨迹；标签4 和5 的行为模式在同一位置生成，行为5 速度是行为4 的2倍，行为4 有200 条轨迹，行为5 有100 条轨迹；标签6 和7 的行为模式在同一位置生成，两者运动方向相反，行为6 有200 条轨迹，行为7 有100 条轨迹；标签8～10 的行为同理标签1～3 生成。如图4所示，其中箭头表示目标的运动方向，相邻轨迹点间隔的长短表示目标的速度大小。

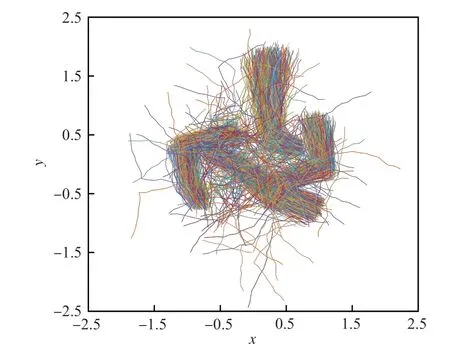
图3 仿真轨迹数据集Fig.3 Plot of simulation trajectory dataset

图4 10 种行为模式Fig.4 Plot of 10 beheavior patterns

4.2 评价指标

本文采用精确率（Precision）、召回率（Recall）、F1-score、分类准确率（Accuracy）以及虚警概率（False Alarm， FA）对算法的性能进行评估。Precision、Recall 以及Fl-score 用来衡量一致性预测器在每一类行为模式上的在线分类性能。其中Precision 表示测试集中某种行为模式正确预测的轨迹个数占所有预测为该种行为模式轨迹总数的比例；Recall 表示测试集中某种行为模式预测正确的轨迹个数占该种行为模式的轨迹总数的比例；Fl-score 是Precision 和Recall的调和平均值。False Alarm 表示判定为离群轨迹的时空轨迹中具有正常行为模式标签的时空轨迹的比例。Accuracy 表示所有行为预测正确的轨迹占测试集所有轨迹总数的比例，用来衡量在线分类和异常检测在整个数据集上的整体性能。这些性能指标的计算方法如下：

4.3 验证与分析

本实验在仿真数据集上实现SSHNN-ICMP算法，并分别与一致性多分类器CMC 与不一致性度量函数HD-KNN、STHD-KNN 的组合进行对比分析。将整个仿真数据集随机分成训练集和测试集，每一种行为模式的时空轨迹中75%作为测试集，25% 作为训练集，对于SSHNNICMP 而言，20%作为压缩样本集，5%作为检验样本集。设置风险水平ε=0.01，K 近邻参数K=2，3，4，5，按照上述比例随机选取训练集和测试集进行20 次重复实验。采用Precision、Recall、F1-score、Accuracy、FA 以及训练和测试消耗的总时间对算法的性能进行评估，如表1 所示，其中的Precision、Recall 和F1-score 为每次实验所有行为模式类别间的平均值，表中的所有数据均为20 次重复试验的平均值，表中每项评估值的最优结果用加粗表示。

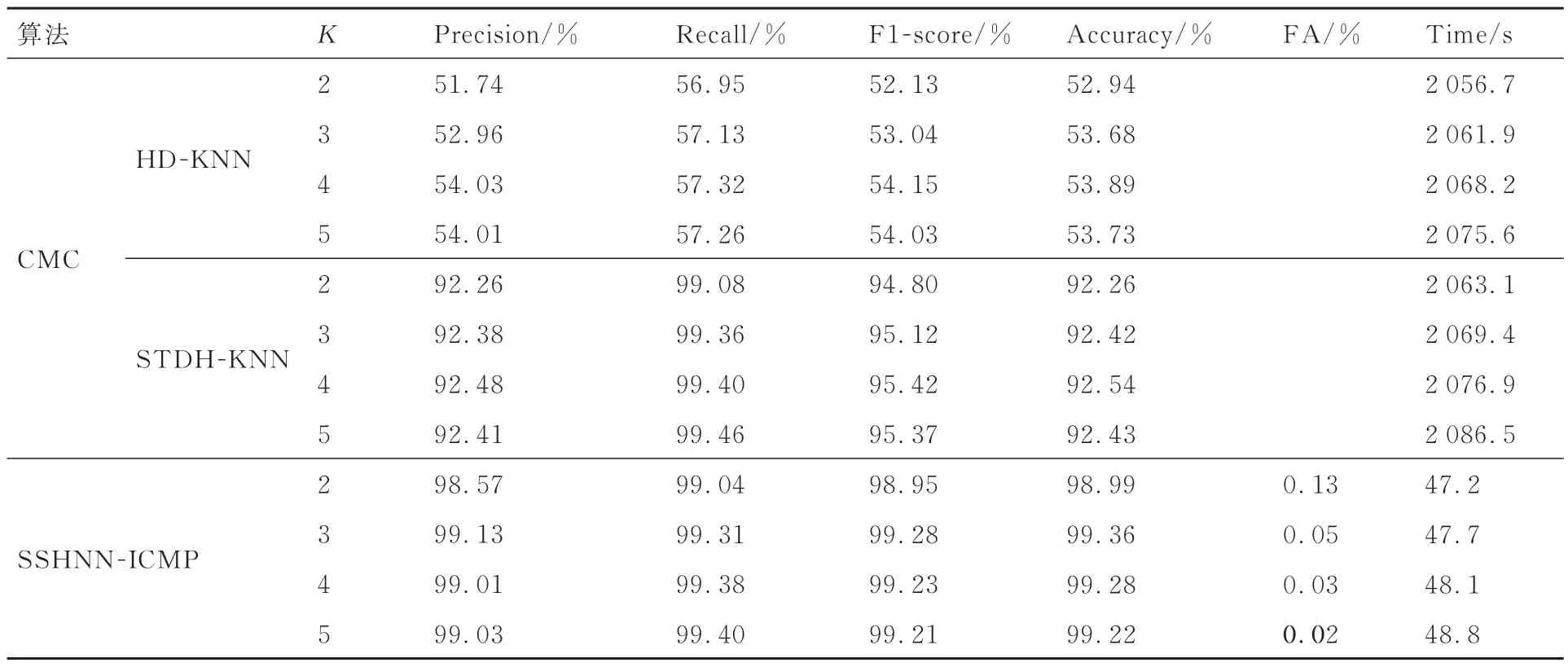
表1 仿真场景中算法性能比较Table 1 Comparison of algorithm performance in simulation scenario

从表1 中结果可以看出，SSHNN-ICMP 与CMC 的组合算法相比在Precision、F1-score 以及Accuracy 等评价指标上具有明显的优势，且预警率保持在较低的水平。STHD 与KNN 的NCM组合整体性能要优于HD 与KNN 的NCM 组合，因为前者具备分辨空间位置相似而速度和航向不同的行为的能力。在训练和测试消耗的总时间上SSHNN-ICMP 要远小于CMC 的组合算法。

为了进一步对比两者在测试轨迹运行时间上的差异，将K=3 时SSHNN-ICMP 与STHDKNN-CMC 在每一条测试轨迹上的耗时变化绘制在图5 中。从图5 中可以看出，随着测试轨迹数目的增加，SSHNN-ICMP 的运行时间几乎保持在一个很低的值不变，而STHD-KNN-CMC随着测试轨迹数目的增加运行时间几乎呈线性增长。因此SSHNN-ICMP 的实时性更强，将更适用于数据集规模大的场景。

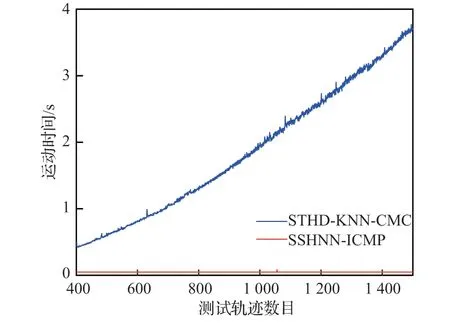
图5 运行时间测试轨迹规模变化对比Fig.5 Comparation of running times dependent on size of test trajectory dataset

由于归纳式一致性预测的训练集不随在线检测更新，因此压缩样本集的规模将决定着预测性能。为了研究SSHNN-ICMP 分类的整体性能与压缩样本集的关系，保持5%的数据集作为检验样本集不变，将压缩样本集按照每一种行为模式从5%开始等比例增加，采用Accuracy 评估性能，通过多项式拟合的方法绘制曲线，如图6 所示。

图6 仿真场景中压缩样本集规模对算法分类准确率的影响Fig.6 Influence of compressed dataset size on Accuracy of algorithm classification in simulation scenario

从图6 可以看出，当压缩样本集轨迹数据量较小的时候，Accuracy 随着压缩样本集规模的增加而逐渐升高；当压缩样本集轨迹数量达到一定规模时，Accuracy 总是保持在一个较高的水平。因此，获得足够的压缩样本集是保证轨迹行为规律预测的准确性的前提。

5 实测数据实验分析

5.1 实测轨迹数据集

本实验选取了2006 年2 月某段时间美国旧金山机场雷达检测出的部分航班飞行轨迹，该实测数据集总计有1 128 条时空轨迹。根据之前的研究工作［29］对该轨迹数据集进行规律挖掘并标记标签，其中包括14 种行为模式和57 条离群轨迹。所有轨迹如图7 所示，不同行为模式的轨迹用不同的颜色表示，离群轨迹用黑色表示。图8展示了该场景下目标的14 种不同的行为模式。

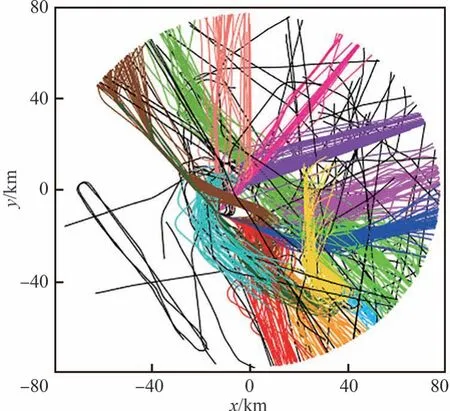
图7 真实轨迹数据集Fig.7 Plot of real trajectory dataset

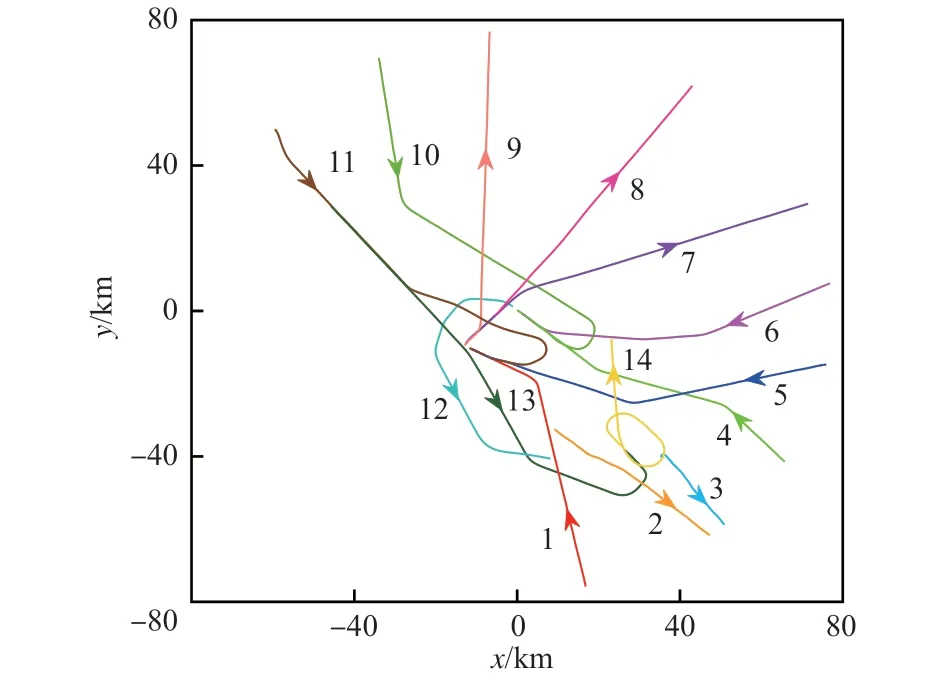
图8 14 种行为模式Fig.8 Plot of 14 beheavior patterns

5.2 实验与分析

本实验在实测数据集上实现了SSHNNICMP 算法，并分别与一致性多分类器CMC 与不一致性度量函数HD-KNN、STHD-KNN 的组合进行对比分析。将整个仿真数据集随机分成训练集和测试集，每一种行为模式的时空轨迹中25%作为测试集，75%作为训练集，对于ICP 而言，20%作为压缩样本集，5%作为检验样本集。设置风险水平ε=0.01，K 近邻参数K=3，按照上述比例随机选取训练集和测试集进行20 次重复实验。采用Precision、Recall、F1-score、Accuracy、FA 以及训练和测试消耗的总时间对算法的性能进行评估，如表2 所示，其中的Precision、Recall 和F1-score 为每次实验所有行为模式类别间的平均值，表中的所有数据均为20 次重复试验的平均值，表中每项评估值的最优结果用加粗表示。

表2 真实场景中算法性能比较Table 2 Comparison of algorithm performance in measured scene

图9 展示了随着压缩样本集规模增大Accuracy 的变化，通过多项式拟合的方法绘制曲线。从图中可以看出，当压缩样本集轨迹数据量较小时，Accuracy 随着压缩样本集规模的增加而逐渐升高；当压缩样本集轨迹数量接近一定数量时，Accuracy 总是保持在一个较高的水平。因此，在实际应用场景中，当压缩样本集轨迹数量足够且适量时，即可保证算法具备良好的准确性和实时性。

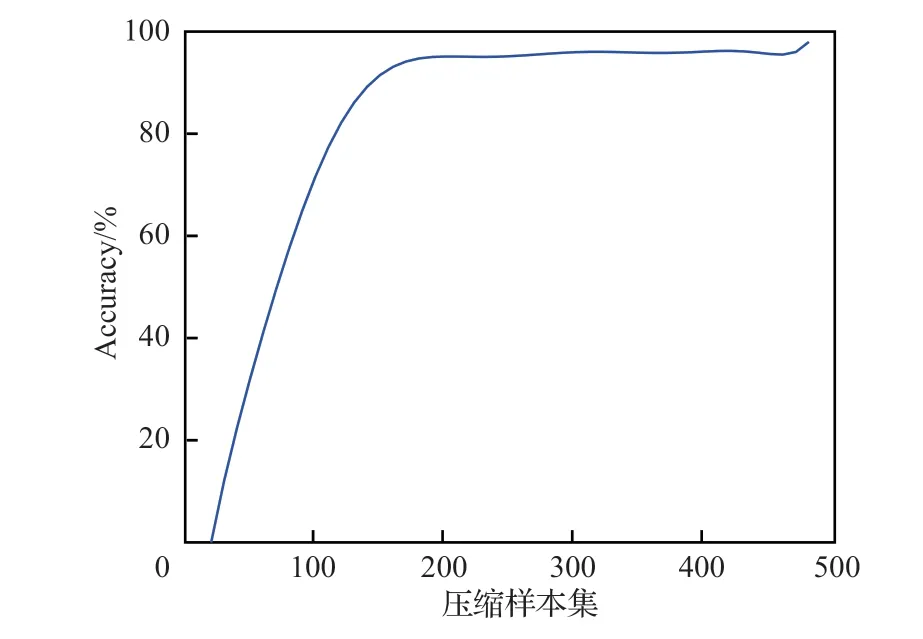
图9 真实场景中压缩样本集规模对算法分类准确率的影响Fig.9 Influence of compressed dataset size on Accuracy of algorithm classification in measured scenario

6 结 论

本文针对实时预警监视需求，提出了基于时空轨迹信息的目标行为模式在线分析方法，进行了实验分析和验证，创新性工作包括几个方面：

1） 提出了ICMP，解决了CMC 实时性不强、对离群轨迹不敏感等问题。

2） 提出了时空Hausdorff 距离概念，并结合KNN 构造了DSHNN-NCM，可以有效区分位置、航向以及速度特征不同的目标行为。

3） 提出了SSHNN-ICMP，可以在预警监视场景下对目标频繁出现的行为进行在线学习和预测。

4） 分别在仿真飞行器轨迹和实测雷达轨迹数据中实现了SSHNN-ICMP，结果表明本文算法与CMC 的组合算法相比在Precision、F1-score 以及Accuracy 等评价指标上具有明显的优势，且实时性显著提高。

基于上述创新工作，下一步将重点研究无监督条件下的目标行为模式在线分析方法。