在线监测系统中音速喷嘴的数值模拟分析

金启航 李天硕 李海洋 段钰锋

(东南大学能源与环境学院, 南京 210096)

(东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)

连续排放监测系统(continuous emission monitoring system,CEMS)具有自动现场采样、测量精度高的优点[1],被广泛应用于烟气污染物的实时在线检测中.根据不同的采样原理,可将其分为稀释抽取式CEMS和源级抽取式CEMS[2].其中,稀释抽取式CEMS具有样气处理量小、正压传输等优点,在国外公司CEMS产品上应用广泛[3].

热稀释模块作为稀释抽取式CEMS的核心部件,主要包含热稀释引射器和音速喷嘴.当前稀释抽取技术普遍存在稀释精度难以控制的问题[4-5],而音速喷嘴计量精度直接影响稀释精度.关于CEMS音速喷嘴的研究主要集中在喷嘴的流量校准方面.KVB-Enertec公司产品[4]在音速喷嘴上加装压力调节系统,以确保进入音速喷嘴的气体压力恒定.Jahnke等[6]发现稀释抽取式CEMS的压力效应,通过软件修正压力变化的影响.文献[2]提出可在稀释探头内增加自动调节温度的加热系统,以确保采样探头在设计温度下运行.然而,上述音速喷嘴校准方法仅为工程经验方法,要提高稀释抽取式CEMS的稀释精度,需要完善CEMS音速喷嘴的结构设计理论和流量预测理论.

ISO 9300:2005(E)规范[7]中提出了一种具有高计量精度的音速喷嘴,在规定雷诺数范围内测量其不确定度小于0.3%.然而,在烟气条件下,应用ISO类音速喷嘴仍存在许多问题.烟气采样时,音速喷嘴喉部雷诺数较低(Red≤10 000),应用时会出现非临界流提前的现象[8],导致喷嘴临界背压比降低,热稀释引射器设计难度增加,稀释比可调范围缩小.部分学者研究了低雷诺数下扩散段参数对临界背压比的影响.Nakao等[9]测试了Red=40～30 000的6块ISO圆环形喷嘴和3块无扩散段扇形喷嘴的临界背压比,发现临界背压比与喉部雷诺数以及音速喷嘴的几何结构有关,且扩散段使得音速喷嘴的临界背压比明显增高.Wright等[10]以多种气体为介质,对79块音速喷嘴进行临界背压测试,提出了临界背压比与雷诺数、喷嘴喉径、扩散段角度以及扩散段长度的经验关系式,但是该关系式仅适用于Red=2 800～240 000的情况,且未考虑非临界流提前现象的发生.由于低雷诺数范围内扩散段参数与临界背压比的定量关系不明确,在CEMS音速喷嘴设计阶段并没有一个明确合适的扩散段参数,故需要确定流出系数与气体种类、扩散段参数以及雷诺数的定量关系,服务于不同扩散段参数的CEMS音速喷嘴.

目前,关于低雷诺数音速喷嘴流出系数的定量关系研究主要分为理论预测模型和经验关系式2类,但现有理论预测模型[11-14]和经验关系式[15-17]均未考虑扩散段参数对流出系数的定量影响.在扩散段参数与流出系数关系的研究中,Ishibashi等[18]、Nakao等[9]的实验结果均显示扩散段对喉径较小的音速喷嘴的流出系数存在影响.Kim等[19-20]利用CFD数值模拟研究了喉径为0.2～5.0 mm的音速喷嘴的流出系数,仿真结果表明随着扩散角的减小,流出系数逐渐降低,且该影响随着雷诺数的减小而增强.丁红兵[21]以喷嘴非黏性多维跨音速流动模型及层流边界层理论为基础,结合CFD及实验数据,分析了ISO类喷嘴扩散段对流出系数的影响机制,但受限于扩散段部分的锥面结构,并未获得流出系数的解析解.

鉴于此,本文基于圆环形喉部音速喷嘴的数值模拟数据以及实验测试结果,提出了一种基于反向传播(back propagation, BP)神经网络的音速喷嘴流出系数预测方法,探究了音速喷嘴的临界背压比与喉部雷诺数关系,提高了CEMS音速喷嘴流量的预测精度,拓宽了ISO类音速喷嘴的应用范围.

1 模型与方法

1.1 音速喷嘴流量计算

图1给出了圆环形喉部喷嘴示意图.图中,d为喉部直径;D为入口截面直径;Rc为收缩段曲率半径;θ为扩散段角度;L为扩散段长度.其进口是曲率半径为Rc的收缩段,扩散段与收缩段轮廓线在喉部后侧相切.音速喷嘴通过预测临界状态下的壅塞效应实现流量测量.当音速喷嘴背压比低于临界压比时,音速喷嘴处于正常工作状态.音速喷嘴的背压比为[9]

图1 ISO 9300圆环形喉部喷嘴示意图

(1)

式中,Pb、P1分别为音速喷嘴的下游压力和上游压力.音速喷嘴临界状态被破坏时的背压比为临界背压比(critical back pressure ratio, CBPR),定义为流出系数达到临界状态流出系数99.9%时的背压比.

对于一维等熵流动,理想气体流过音速喷嘴的质量流量qmi为[21]

(2)

(3)

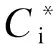
对于实际流动过程,需要考虑气体黏性、流动多维性、真实气体物性等的影响.因此,音速喷嘴的实际质量流量qm为[21]

(4)

Cd=Cd,1Cd,2

(5)

式中,Cd,1、Cd,2分别由文献[12,14]中的理论预测模型计算得到,即

(6)

(7)

(8)

(9)

式中,μ0为滞止条件下的动力黏度.

1.2 数值方案

本文音速喷嘴模型采用旋转对称模型,入口截面直径为2.5d.二维网格划分采用结构型四边形网格,壁面采用加密网格(见图2).求解器采用适合于跨音速流动的密度基形式,求解格式选用稳定性和收敛性更好的隐格式.流动介质密度计算采用真实气体Redlich-Kwong形式状态方程,黏性计算采用Sutherland公式,定压比热容采用温度的五阶多项式近似.进出口均为压力边界条件,通过调节出口压力使音速喷嘴背压比低于0.1,确保音速喷嘴处于临界状态.湍流强度计算公式为[21]

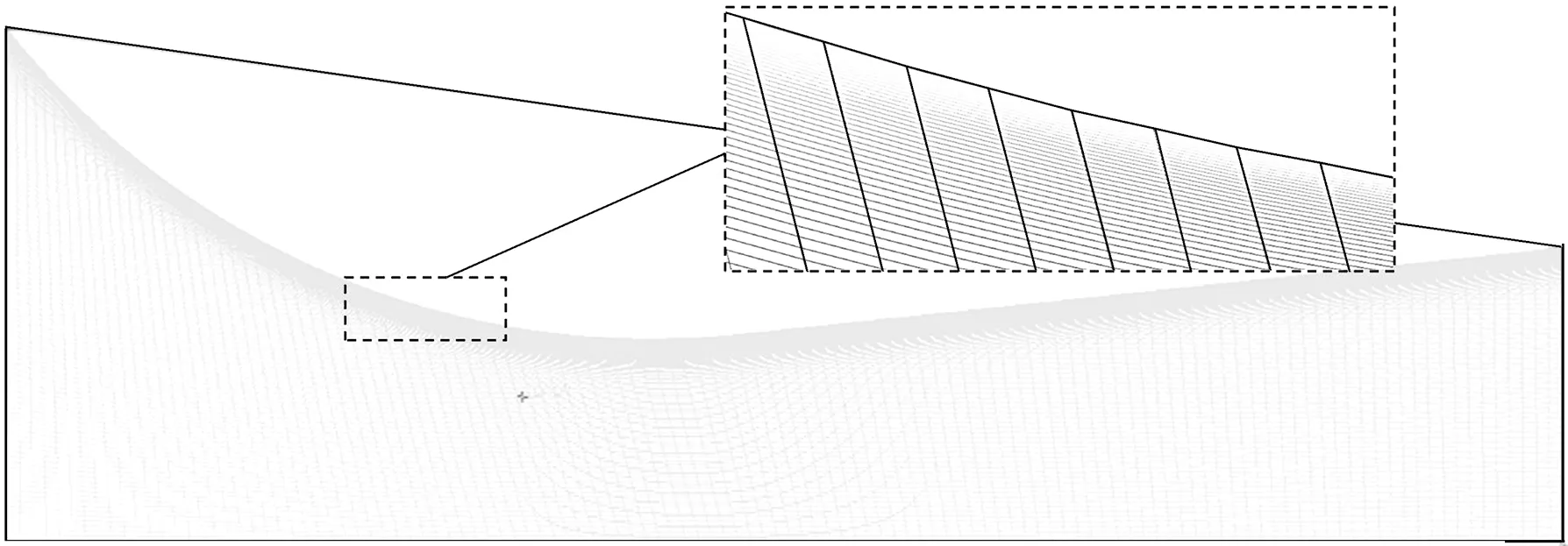
图2 壁面加密的网格划分

(10)

式中,ReHD表示以当地水力直径为特征长度的雷诺数.

为达到最佳计算效果和精度,需权衡离散误差和舍入误差.以扩散段长度L=2d、扩散角θ=4°的音速喷嘴为例,网格无关性测试结果见图3.当横向网格数N1由120增加至140时,音速喷嘴质量流量变化量仅为0.039 9%,由此确定横向网格数N1=120.当纵向网格数N2由120增加至140时,音速喷嘴质量流量变化量仅为-0.040 0%,由此确定纵向网格数N2=120.

(a) N1=120

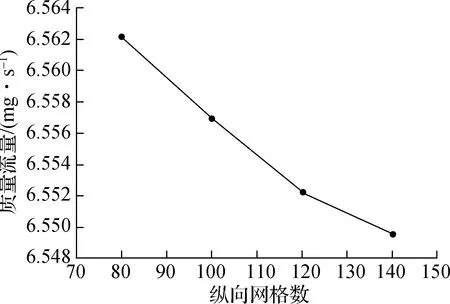
(b) N2=120

1.3 模拟结果验证

采用文献[9,23]中喉部直径为0.593 5和0.103 0 mm的音速喷嘴(L=3d、θ=3°)的实验数据,验证本文数值方案的可靠性,结果见图4.由图可知,数值模拟结果与文献[9,23]实验数据基本一致,可以反映音速喷嘴在低雷诺数下的流动特性.当Red<3 900时,采用层流模型进行数值模拟相对误差最小,小于2%.当Red>3 900时,采用雷诺应力模型相对误差小于0.2%.Kliegel-Levine-Geropp(KLG)模型对L=3d、θ=3°的音速喷嘴流出系数具有较高的预测精度.

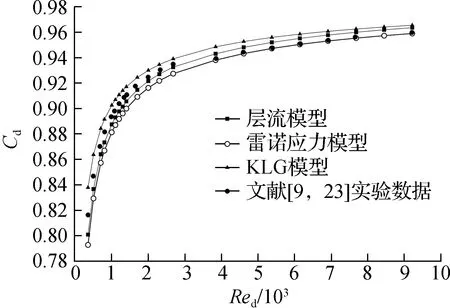
(a) 流出系数

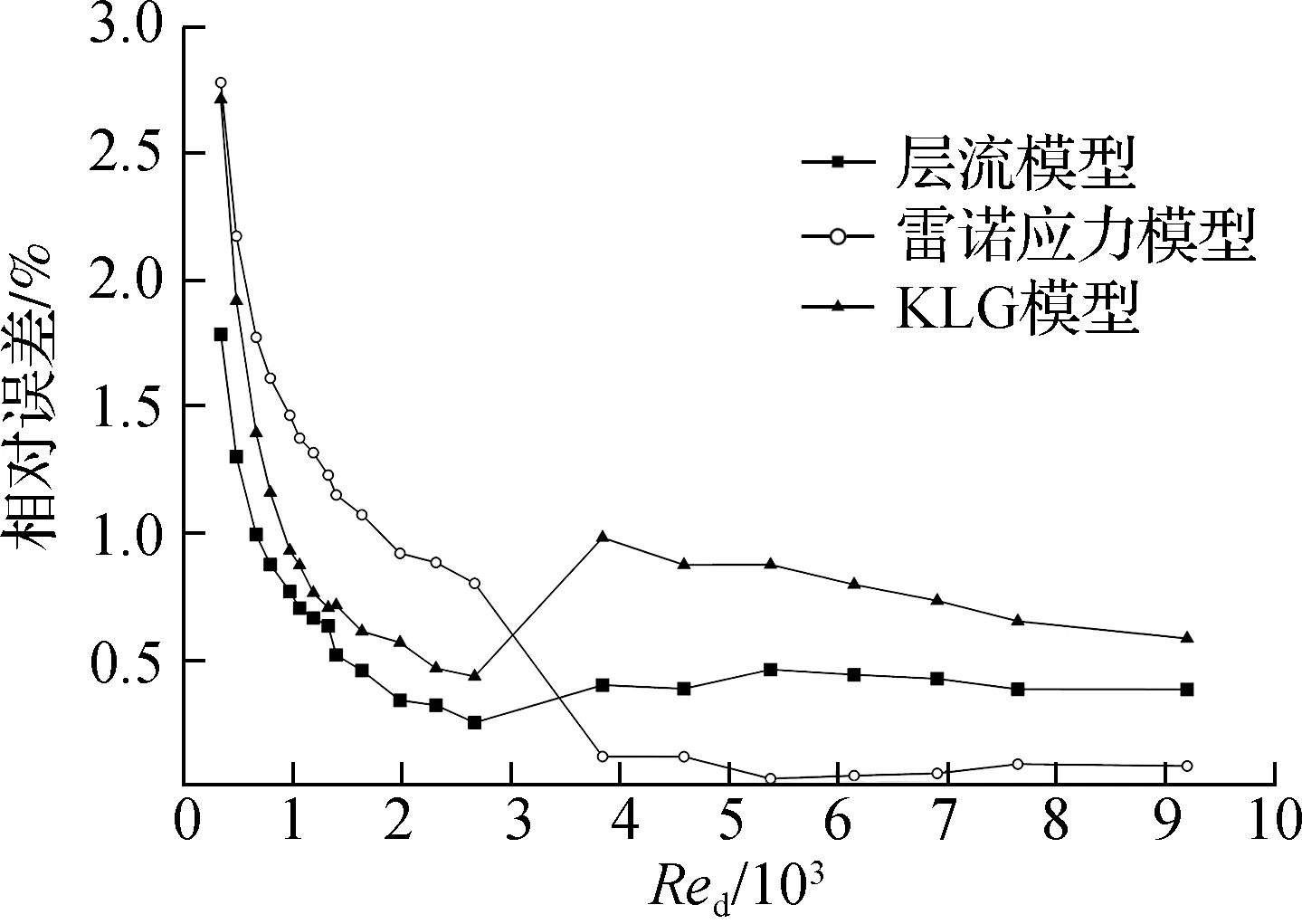
(b) 相对误差

1.4 BP神经网络模型

BP神经网络模型由输入层、隐藏层、输出层构成,其原理是根据输入数据集合,利用优化算法对神经网络层与层之间的权值和阈值进行优化,最终获得满足预测精度的神经网络参数,应用于输出值的预测.

图5给出了本文建立的3-5-1型BP神经网络模型示意图.图中,wi,j表示第j个输入参数输入第i个隐含层神经元的权重;bi表示第i个隐含层神经元的阈值;ki表示第i个隐含层神经元输出层神经元的权重;S1表示输出层神经元的阈值.隐含层神经元选用tansig函数,输出层神经元选用线性函数,以Levenberg-Marquardt算法进行网络训练.以数值模拟获得的数据作为数据集,利用BP神经网络反映结构参数、气体种类以及雷诺数与流出系数之间的非线性映射关系.

图5 3-5-1型BP神经网络模型示意图

1.5 实验装置

采用如图6所示的实验装置,对音速喷嘴的流出系数和临界背压比进行测试.该装置主要由样气源(空气)、稀释气源(氮气)、质量流量计、压力表、温度表、音速喷嘴以及热稀释引射器组成.稀释气进入热稀释引射器内,在引射器真空室产生负压,从而引射样气(空气)流过音速喷嘴.在实验过程中,通过调节稀释气的气量,控制音速喷嘴下游的真空度.当背压比为0.25时,认为音速喷嘴已经处于临界状态.

图6 音速喷嘴实验装置示意图

2 结果与讨论

2.1 音速喷嘴雷诺数分析

烟道内温度和压力波动是影响音速喷嘴采样稳定性的关键因素,因此需要研究喉口直径、温度和压力对音速喷嘴喉部雷诺数的影响,确定音速喷嘴工作雷诺数的范围.为简化计算过程,本节以氮气为介质,进行音速喉部雷诺数计算.

图7给出了氮气条件下d=0.15 mm的音速喷嘴喉部雷诺数等高线图.由图可知,喉部雷诺数随着总温降低非线性增加,随着总压升高线性增加.总压下降时,升高总温可使喉部雷诺数保持不变.在所计算的总温总压范围内,音速喷嘴的喉部雷诺数为1 000～8 000,属于低雷诺数流动[21],此时需要考虑扩散段参数对流出系数的影响.在烟气取样条件(P0=101 kPa)下,雷诺数变化范围约为1 000～3 000.

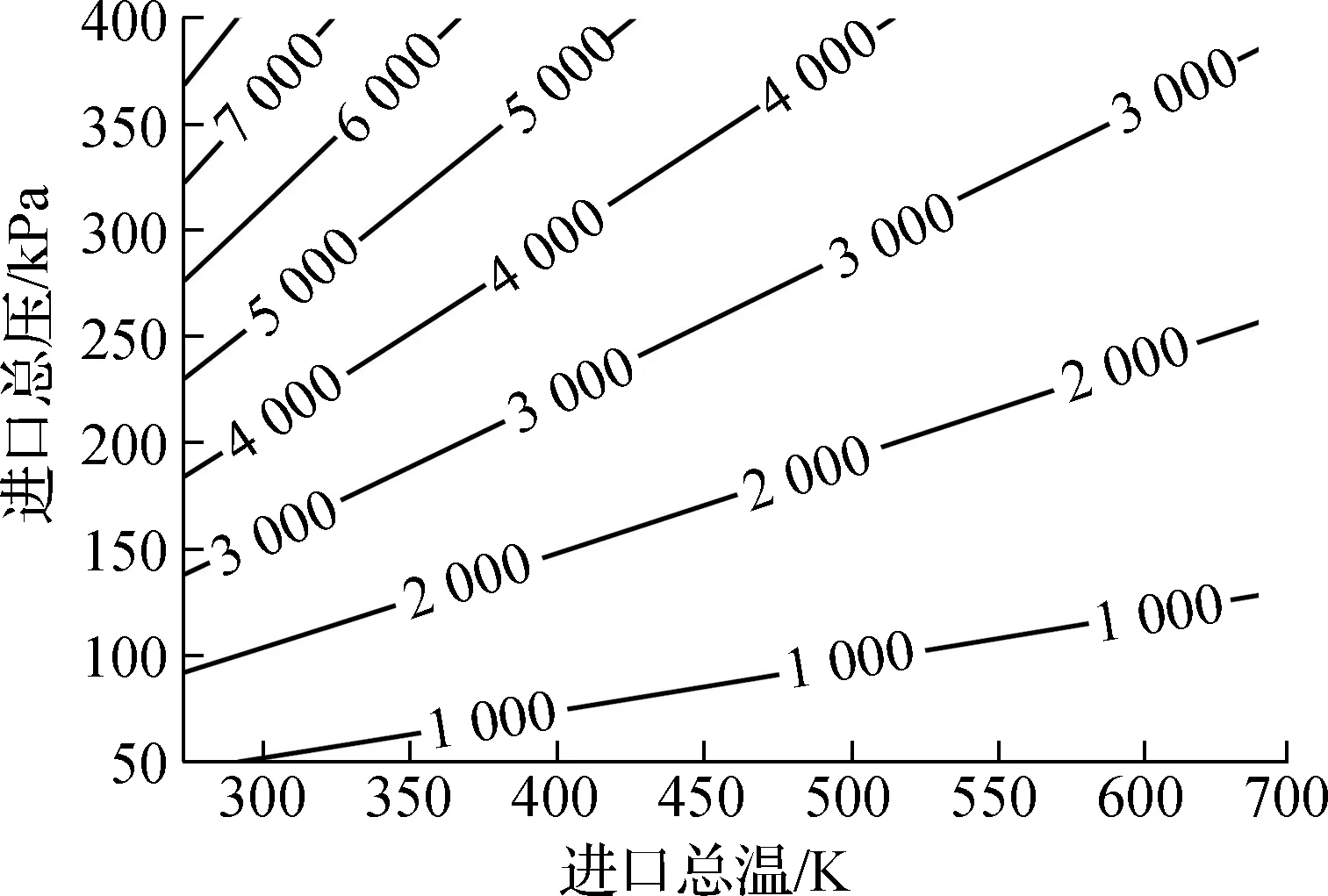
图7 音速喷嘴喉部雷诺数与进口总温总压关系

为探究喉径对雷诺数的影响,将式(2)代入式(8)得

(11)

气体动力黏度μ0通常为温度的函数,可由Sutherland公式计算得到.由式(11)可知,雷诺数与音速喷嘴喉径成正比.稀释抽取式CEMS在选用不同稀释比时,喷嘴喉径可能不同,当喉径为0.5 mm时雷诺数约为3 000～10 000.因此,本文对Red=400～10 000条件下的音速喷嘴流动特性进行研究.

2.2 临界背压比与雷诺数关系

临界背压比作为衡量音速喷嘴运行可靠性的关键参数,在CEMS系统设计时需要优先考虑.为降低音速喷嘴的设计成本,可利用数值模拟对喉部雷诺数与临界背压比关系进行预测.在低雷诺数条件下对音速喷嘴(θ=3°、L=3d、Rc=2d)临界背压比进行数值模拟,并与文献[9]中的实验结果进行对比(见图8).

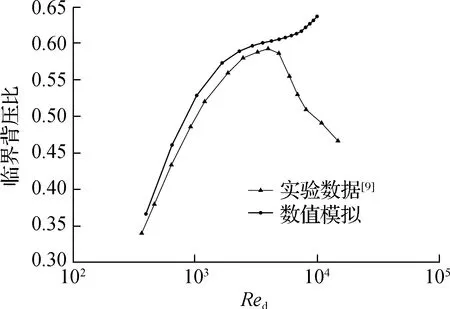
图8 音速喷嘴临界背压比与喉部雷诺数关系

由图8可知,受扩散段内激波与边界层之间相互作用的影响,当喉部雷诺数大于4 000时,可观察到非临界流提前现象[8].然而,由于数值模拟无法反映激波与边界层之间的复杂作用,结果逐渐偏离实验结果.根据2.1节中的计算结果,设计音速喷嘴时,令喉部直径小于0.2 mm,喉部雷诺数小于4 000,可以避免非临界流提前现象造成的数值模拟结果误差以及临界背压比误判.

2.3 扩散段参数对流出系数的影响

为研究低雷诺数下音速喷嘴扩散段结构对流出系数的影响,对不同扩散段结构进行了流动特性模拟.图9给出了氮气条件下d=0.15 mm、Rc=2d的音速喷嘴在不同雷诺数下的流出系数模拟结果.

由图9可知,在相同雷诺数和扩散段结构参数的条件下,流出系数误差小于0.03%,在数值模拟中可以忽略不计.因此,在数值模拟中可忽略流体的总温T0、总压P0以及喉径d对流出系数的影响.扩散段参数对流出系数具有较大影响,随着雷诺数的增大,扩散段参数对流出系数的影响逐渐减小.目前采用的大部分定量预测关系式忽略了扩散段参数对流出系数的影响,将导致结果产生较大误差.后文中选取KLG模型,采用精度较高的扩散段参数进行研究,即1.3节中L=3d、θ=3°的音速喷嘴结构.

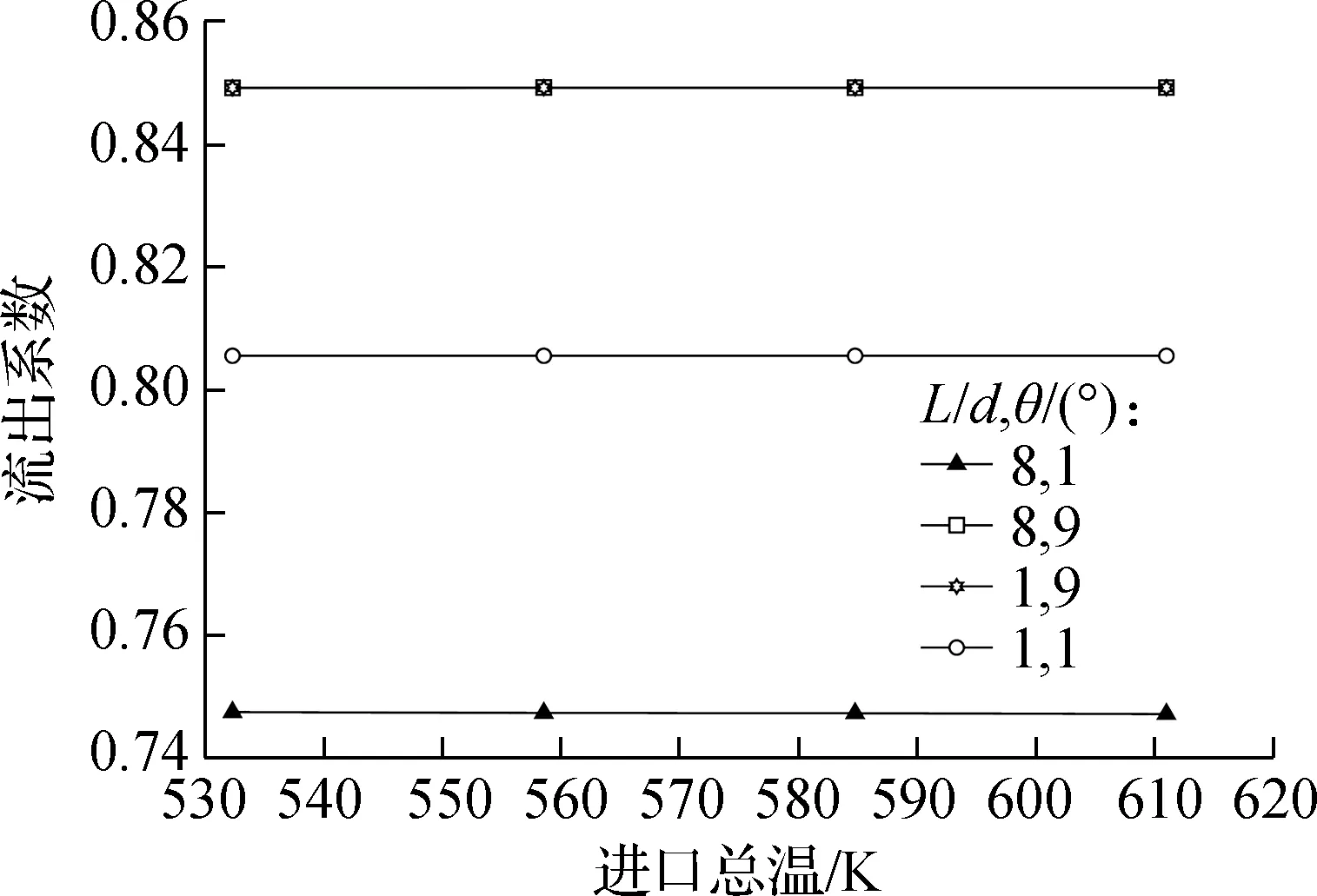
(a) Red=500

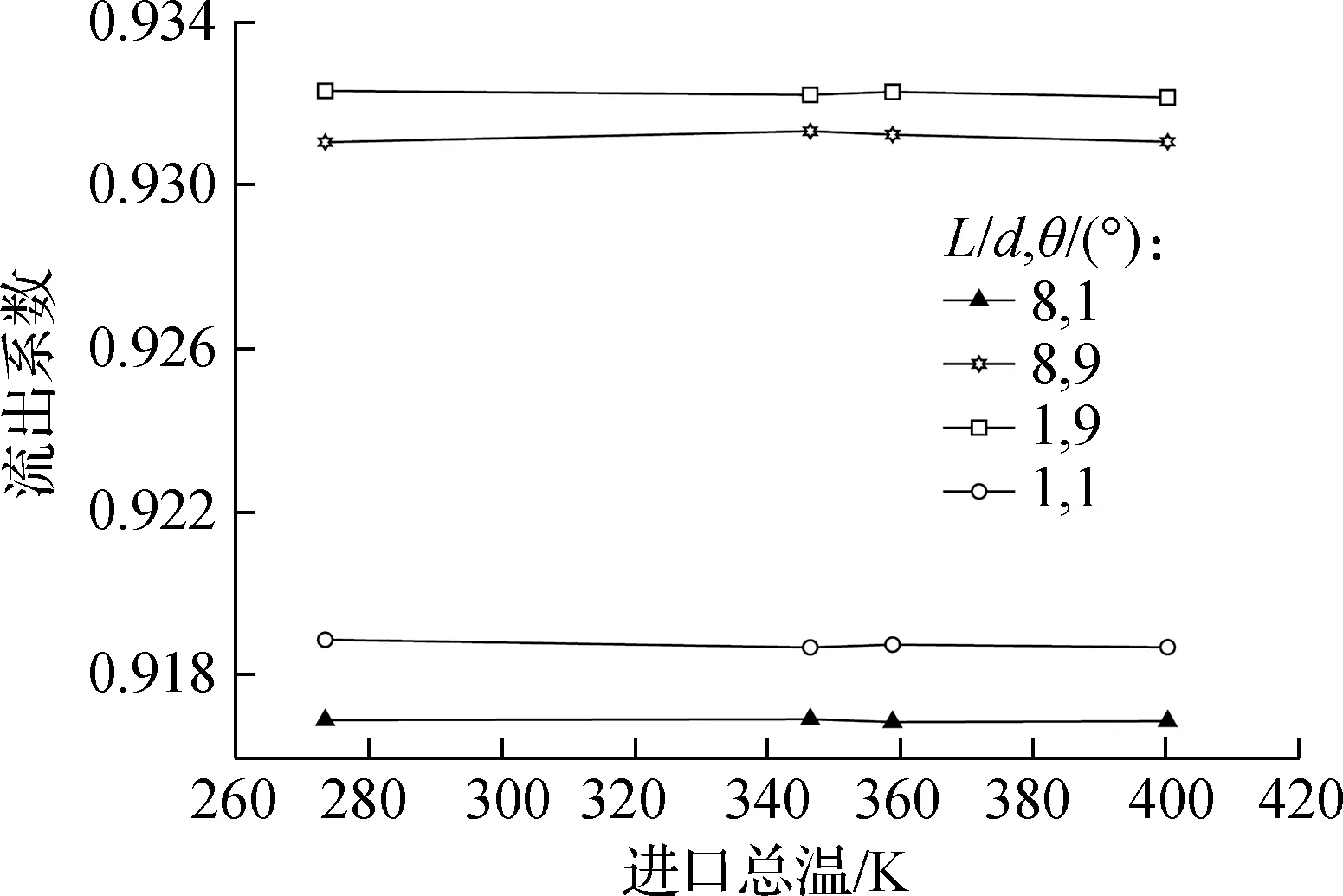
(b) Red=3 000

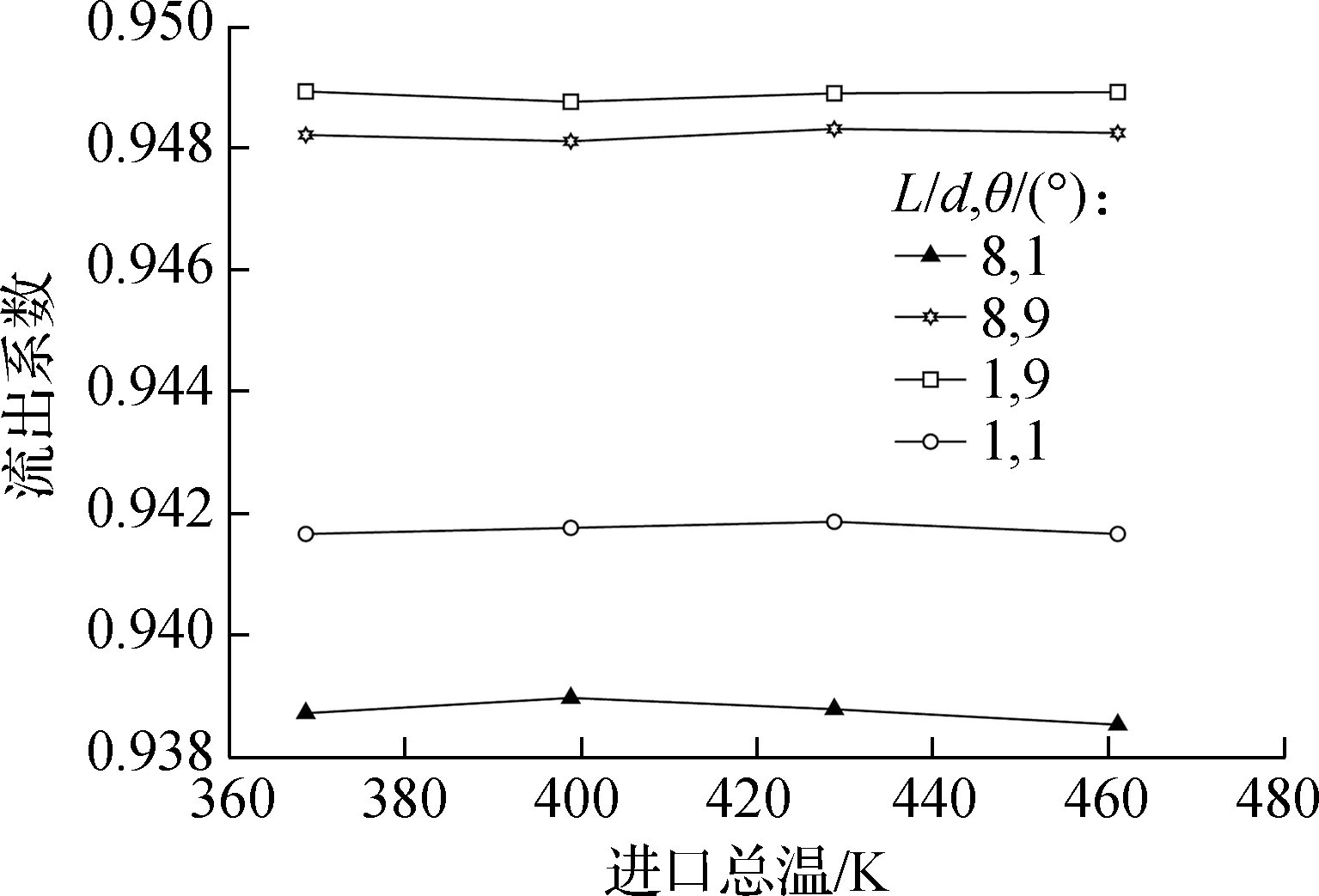
(c) Red=5 500

(d) Red=8 000

2.4 收缩段参数与流出系数的定量关系

为在烟气条件下应用音速喷嘴,首先研究流出系数与气体种类、收缩段参数以及雷诺数的定量关系.本文采用的3-5-1型BP神经网络模型(见图5),将气体等熵指数、收缩段参数、雷诺数3个无量纲参数作为输入,选择丙烷(C3H8)、乙炔(C2H2)、甲烷(CH4)、氮气(N2)、氩气(Ar)作为仿真介质,其等熵指数分别为1.135、1.238、1.306、1.404、1.669[23],在Rc=d～5d、Red=400～10 000的条件下获得125组数值模拟数据.这些数据被随机划分为训练集、验证集以及测试集,进行BP神经网络训练,训练误差见表1.

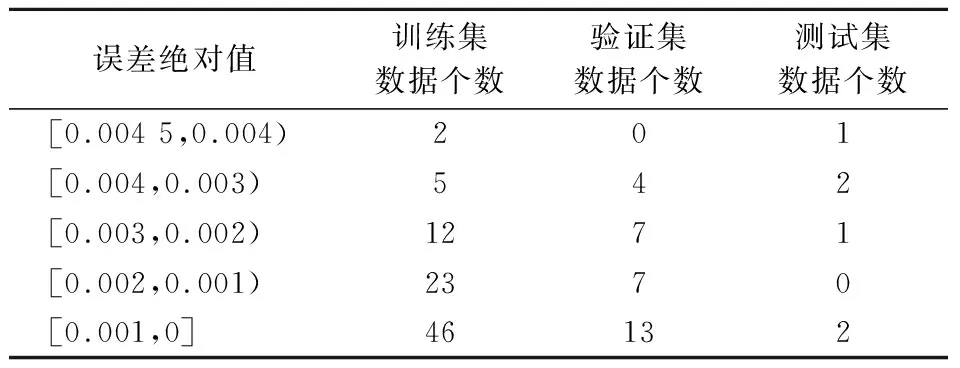
表1 收缩段BP神经网络训练结果误差分布

由表1可知,3-5-1型BP神经网络可以较好地反映流出系数与气体种类、收缩段参数以及雷诺数的定量关系.125组数据组成的验证集、测试集、训练集与BP神经网络模型的误差的绝对值不超过0.004 5,表明BP神经网络模型训练结果较好,没有明显的过拟合或欠拟合现象.采用约4×107组相应范围内计算所得的KLG模型数据作为测试数据,误差结果见图10.

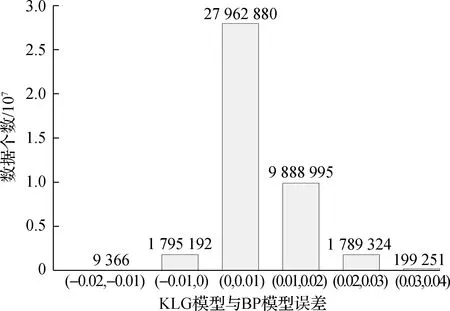
图10 BP神经网络测试结果误差分布

由图可知,BP神经网络模型与KLG模型流出系数误差绝对值不超过0.04,且95%的数据误差绝对值不超过0.02.因此,可以认为BP神经网络训练所得模型可靠性较高,可应用于反映流出系数与气体种类、收缩段参数以及雷诺数的定量关系.

2.5 扩散段参数与流出系数的定量关系

文献[24]指出,边界层完全发展,低雷诺数条件下某一固定扩散角的音速喷嘴的流出系数随着扩散段长度增加而趋于一个恒定值.因此,本文仅研究扩散段长度足够长(即增加扩散段长度时流出系数不再变化)的情况.采用2.3节中可靠性验证获得的BP神经网络方法,建立流出系数与扩散段角度、气体种类以及雷诺数的定量关系.

文献[7]建议音速喷嘴建议的收缩段曲率半径为1.8d～2.2d,故本文将收缩段参数选取2d.参考2.4节步骤,在θ=1°～9°、Red=400～10 000的条件下,获得125组数值模拟数据,建立3-5-1型BP神经网络,其训练误差分布见表2.由表可知,125组数据组成的验证集、测试集、训练集与BP神经网络模型的误差绝对值不超过0.009.

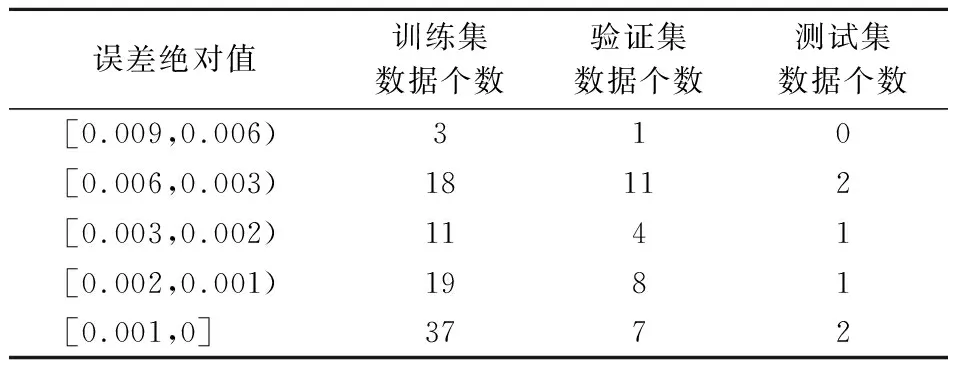
表2 扩散段BP神经网络训练结果误差分布

以表3中某75 t/h循环流化床锅炉燃煤电厂实测烟气(主要成分为N2、O2、CO2、H2O)数据作为BP神经网络的输入,预测4个测点的流出系数,并与数值模拟结果进行对比,结果见表4.在BP神经网络预测以及数值模拟过程中,当水蒸气体积分数大于5%时,烟气黏度根据文献[25]中的Wilke公式计算得到.

表3 某75 t/h循环流化床锅炉燃煤电厂4个测点参数

表4 不同扩散段角度音速喷嘴流出系数

由表4可知,BP神经网络方法与数值模拟方法的最大误差仅为0.645%,表明BP神经网络方法建立的流出系数与扩散段角度、气体种类以及雷诺数的定量关系具有较高的可靠性,可以代替数值模拟进行采样时烟气流出系数的快速预测.

2.6 音速喷嘴实验验证

利用图6所示实验装置,在T0=293.15 K、P0=101.6 kPa的条件下,以空气为流动介质,对θ=4°、L=6d、Rc=2d的喉径为0.143 2和0.350 2 mm音速喷嘴进行测试.音速喷嘴背压比对其流量的影响曲线见图11.

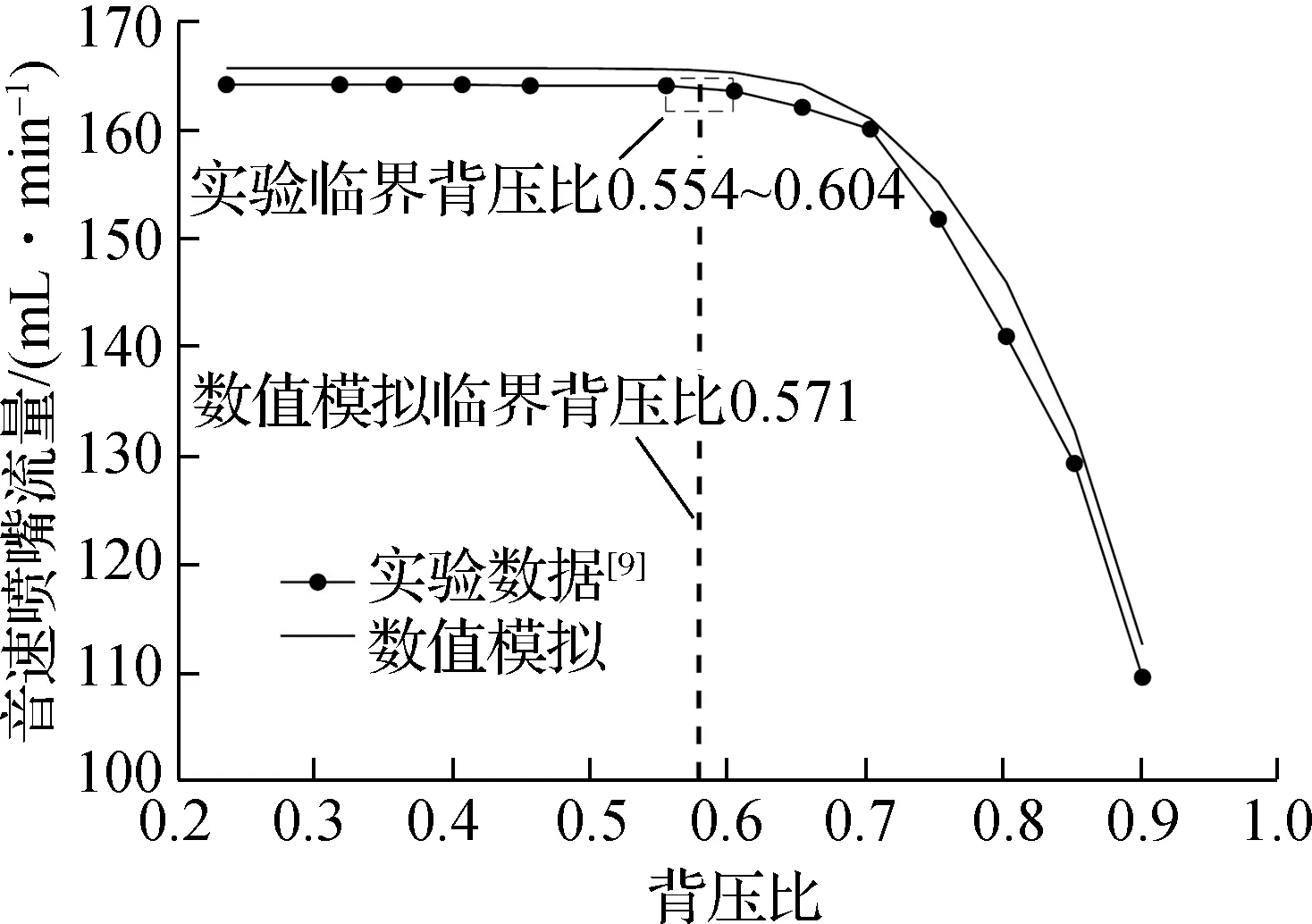
(a) d=0.143 2 mm

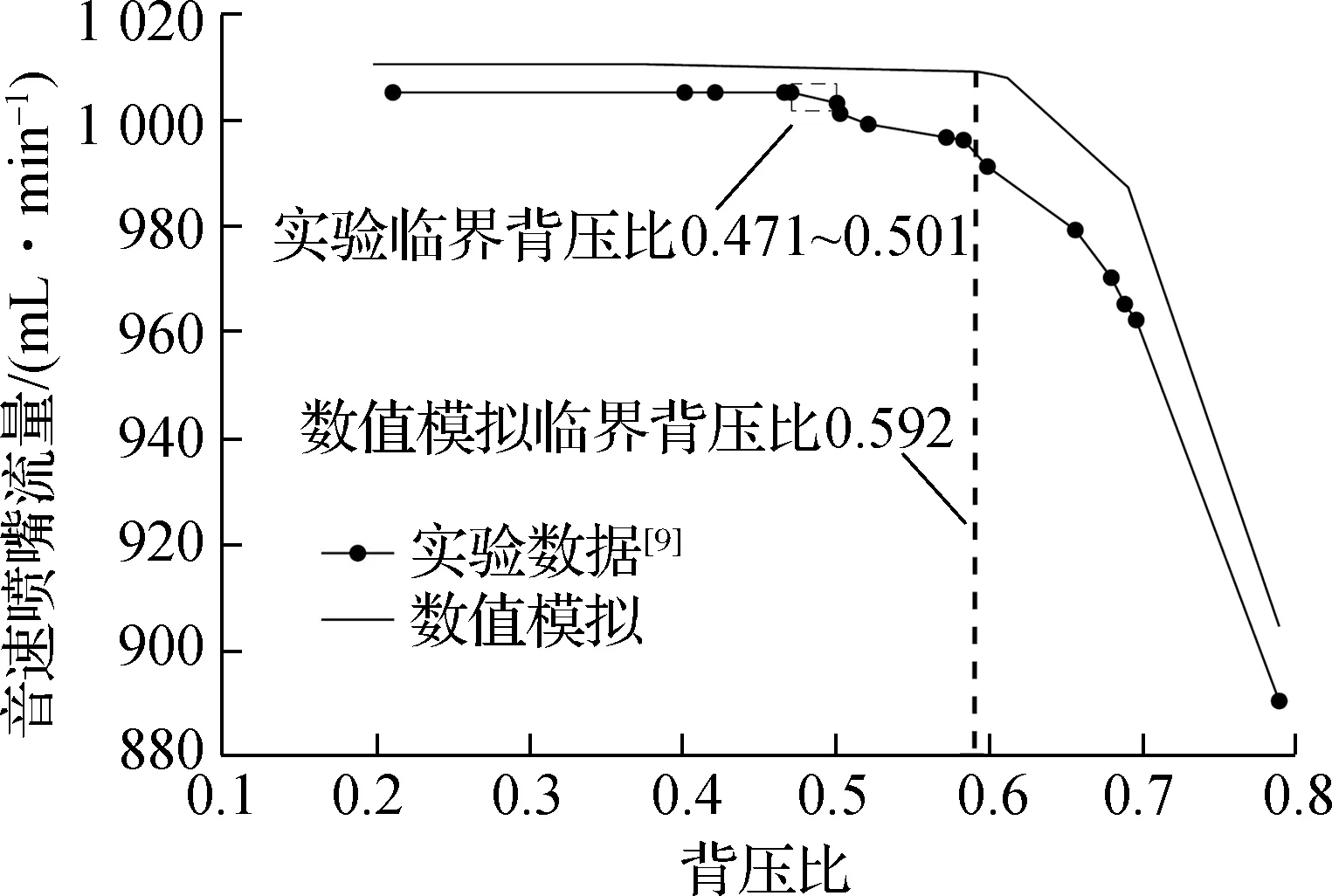
(b) d=0.350 2 mm

由图11可知,随着背压比的减小,音速喷嘴流量不断增大.当喷嘴前后压比低于临界压比时,喷嘴流量达到恒流.对于d=0.143 2 mm的音速喷嘴,数值模拟结果与实验数据之间的流量误差最大不超过3.5%,恒流流量误差为0.588%.受制于质量流量计测量精度,实验测试所得临界压比为0.554～0.604.数值模拟所得的临界背压比为0.571,与实验测试结果相符,说明此时数值模拟能够可靠地反映音速喷嘴内部的流动特性.当喷嘴喉径增大为0.350 2 mm时,数值模拟结果与实验数据之间的恒流流量误差为0.515%,但由于其喉部雷诺数超过4 000,扩散段激波与边界层存在相互作用,音速喷嘴的临界压比降低为0.471～0.501,相较数值模拟值0.592降低约20%.因此,设计喉径较大(d>0.2 mm)的CEMS音速喷嘴时,应考虑设计临界背压比下降的问题.

表5为BP神经网络预测、数值模拟计算以及实验数据的音速喷嘴流动参数.由表可知,BP神经网络方法与数值模拟均可较好地预测音速喷嘴流量,最大误差为1.004%.通过音速喷嘴实验测试,验证了本文方法的可靠性,为烟气条件下音速喷嘴流出系数的快速预测提供了理论参考.

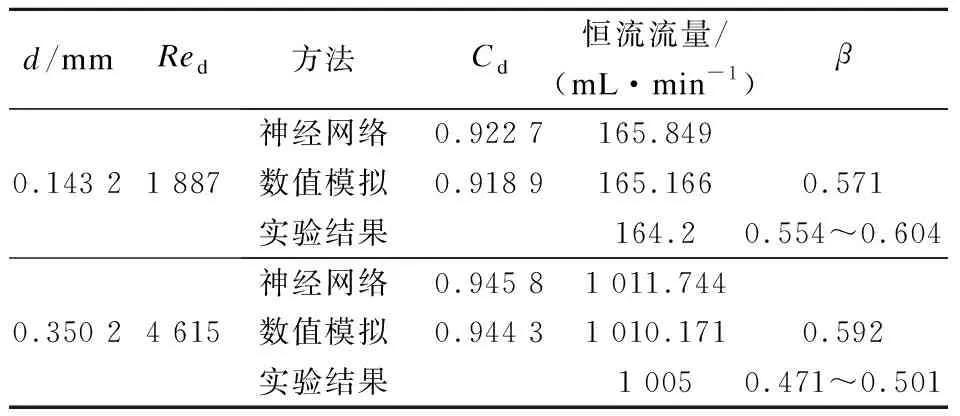
表5 音速喷嘴流动参数

3 结论

1) 雷诺数不变时,可以忽略流体的总温T0、总压P0对流出系数的影响,且总压下降时,升高总温可使喉部雷诺数保持不变.可以通过调整烟气采样时的伴热温度,保持音速喷嘴喉部流出系数不变,提高音速喷嘴流量预测精度.

2) 在烟气条件下,喉部直径小于0.5 mm的音速喷嘴内部流动为雷诺数小于10 000的低雷诺数流动,此时扩散段参数会对音速喷嘴流出系数造成较大影响,且该影响随着雷诺数的减小而增强.在设计应用于烟气采样的ISO类音速喷嘴时,应重视扩散段参数的影响.

3) 喉部雷诺数大于4 000时,非临界流提前现象将造成数值模拟所得的临界背压比产生较大误差.这是因为数值模型无法反映激波与边界层的复杂作用,逐渐偏离实验结果.因此,应根据实际需求选择适当的喉径,并重点关注临界背压比实验值的误判以及数值模拟结果误差.

4) BP神经网络方法利用数值模拟数据训练BP神经网络模型,可较好地预测流出系数与气体种类、结构参数及雷诺数的定量关系.该方法为确定音速喷嘴相关参数的定量关系提供了新思路.