基于证据理论的支挡型黄土高陡边坡稳定性评价
李 哲 刘 彤 刘路路,2,3 韩 猛,4 官宸慧,5 张庭顺
(1长安大学公路学院, 西安 710054)
(2东南大学交通学院, 南京 211189)
(3中国矿业大学深部岩土力学于地下工程国家重点实验室, 徐州 221116)
(4大连理工大学土木工程学院, 大连 116024)
(5武汉大学土木工程学院, 武汉 430072)
随着国家“一带一路”和“交通强国”发展规划的提出,我国高速公路、铁路建设正向地势复杂,地形多以山谷、高原和丘陵为主的西北黄土高原地区快速发展,而更为复杂的地质环境则为边坡设计带来了挑战,并进一步对高陡边坡稳定性的研究提出了更高的要求[1-3].现有的研究常集中于低边坡坡面的稳定性,忽略了支挡结构的稳定性,而高陡边坡的稳定性由边坡坡体和支挡结构两者共同决定[4-6],因此将二者有机结合并建立完善的评价体系是亟待解决的问题.
近年来,国内外不少学者对边坡的安全评价问题进行了大量研究,提出了一些边坡稳定性评价方法[7-9].人工神经网络具有自组织、自学习的特点,能较好地处理边坡的非线性映射,但推理过程不透明,部分影响因素采用人为赋值的方法计算.Acharyya等[10]建立了一个人工神经网格,对条状地基的极限承载力进行了评价,并按其重要程度进行了分类;李蕾[11]利用GA-LM-BP人工神经网络对某特定自然降水环境下的边坡进行了稳定性分析.灰关联法是信息较少时系统的有效方法,但在进行聚类分析时,主观判断对功效函数的确定影响很大.Hao等[12]提出了一个基于区域划分的灰色体系模型,来研究人为因素对流域的作用;冯忠居等[13]基于灰色系统原理,提出用于混凝土动态弹性模量的动态响应模型.模糊综合评价法采用隶属函数评价边坡稳定性,该方法具有系统性强、结果清晰的特点,但各指标权重的分配人为主观因素多.Greco等[14]、Zeng等[15]建立了模糊评价模型,研究岩石跳动距离计算方法和典型滑坡前期预报;孙欣[16]用模糊综合评判法和GIS技术评价边坡稳定性,评价结果与数值模拟结果吻合.还有学者用可靠度分析边坡的稳定性,如罗强等[17]采用可接受部分单元边坡失稳的K/N(F)系统模型,对长区段路基边坡系统安全性进行概率评价;朱聪聪[18]将可靠度理论引入到高边坡工程的稳定性分析中,得到了高边坡失稳的可靠性指数和发生失稳的概率.有时仅用一种方法并不能很好地评价边坡稳定性,可将2种或多种方法相结合进行研究.如张学喜[19]提出了一种将BP神经网络与各因子的非线性关系相结合的快速遗传算法,用以评价边坡稳定性;夏炜洋[20]基于灰色关联度分析影响边坡稳定性因素的关联性,结合BP神经网络对边坡的发展趋势进行了预测.
由于支挡型黄土高陡边坡稳定性评价具有模糊性和不确定性,与上述方法相比,D-S证据理论的推理程序更为严密,且对信息的整合更为完备,并且评价精度较高,但目前在边坡稳定性评估中引入证据推理方法的研究尚少.本文应用边坡稳定性评价体系,建立评价模型,对包茂高速典型支挡型高陡边坡进行安全评价,并得出边坡变化过程中各参数随时间变化的动态变化规律,从而为类似工程稳定性评价提供新思路.
1 D-S证据理论及基于证据理论的评价方法
1.1 基本函数
证据理论是由Dempster于1967年提出的一种不精确推理理论,也称为D-S证据理论,在解决受多因素、多指标影响下的不确定性问题方面应用广泛,尤其是其计算公式被广泛地用于数据融合[21-24].Shafer[25]将在模式识别中判定的问题所有可能的答案都包含在一个非空有限集合Θ中.
定义1设Θ为辨识框架,R为幂集2Θ中一个集类,A为Θ的子集,若函数m:R→[0,1]满足
(1)
函数m为辨识框架上的基本概率分配函数,对任意的命题A,m(A)称为命题A的基本概率分配.
定义2设Θ为辨识框架,R为幂集2Θ中一个集类,A为Θ的子集,m为Θ上的mass函数,Bel:R→[0,1]满足
(2)
Bel称为辨识框架Θ上的置信函数,对任意的命题A,Bel(A)称为命题A的可信度,表示给予命题A的全部的可信程度.
1.2 基于证据理论的不确定性多指标评价方法
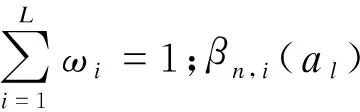
mn,i(al)=ωiβn,i(al)
i=1,2,…,L;l=1,2,…,S
(3)
(4)
式中,mn,i(al)(i=1,2,…,L)表示Ek(i)前i个指标支持假设E被评为Hn等级的置信度;mH,i(al)表示未分配给前i个指标的置信度.
(5)
(6)
2 安全评价模型
2.1 识别框架建立
根据岩土边坡稳定性评价常采用的稳定级别,将稳定性分为4个等级(见表1)[27]:安全状态、基本安全状态、临界状态、破坏状态.这4种评价结果完整地描述了某一边坡安全状态且相互排斥,即Θ={Ⅰ,Ⅱ,Ⅲ,Ⅳ}.

表1 支挡型黄土高陡边坡稳定性等级评价标准
2.2 基本概率分配函数的确定
目前广泛使用的是康兵义等[28]提出的基于区间的基本概率分配函数生成方法,下面简单介绍区间的定义.
定义3设A=[a1,a2]和B=[b1,b2]为2个区间,则它们距离的二次方D2为
(7)
定义4设A=[a1,a2]和B=[b1,b2]为2个区间数,则区间A、B的相似度S(A,B)为
(8)
式中,α>0为支持系数;D(A,B)为区间数A和B之间的距离,可以调节相似性数值的离散度.
采用区间求解基本概率分配的具体步骤如下:
① 将确定的基本指标的区间划分结果作为区间数模型.
② 将各指标的试验数据、监测数据取值构成的区间作为识别区间.
③ 根据式(7)计算2个区间之间的距离.
④ 根据式(8)计算2个区间之间的相似度.
⑤ 对相似度进行归一化处理,即可得到基本概率赋值.
2.3 D-S置信度公式
在得到基础概率数值后,再计算权重的基础概率赋值.指标基础概率分布的计算过程如式(3)~(6)所示.根据Yang[26]的观点,在边坡安全评价时所选择的基本指标中,既有定量指标如日降雨量、孔隙水压力等,也有定性指标如边坡形态、坡体裂隙等.定性指标是指需要将评价指标在各自辨识框架上的置信度转到总的辨识框架上,转移后置信度和不确定度的计算过程如下:
(9)
Hn:βn(al)=δmn,l(L)(al)
(10)
(11)
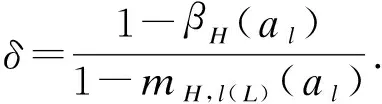
2.4 支挡型黄土边坡指标选择
支挡型黄土边坡安全性评价指标分为边坡坡体和支挡结构2个方面.边坡坡体稳定性的影响因素众多,内部因素主要包括土的性质、结构、地应力以及土体中水的作用等;外部条件主要包括气象特征、地震、边坡形态的改变等.因此,在进行边坡坡体体系构建时,需要全面考虑影响坡体稳定的内外因素.对于自身不稳定的边坡,采用支挡结构是目前比较常用的手段之一.本文支挡结构以抗滑桩为例,当边坡失稳时,滑坡产生的滑坡推力作用在抗滑桩上,抗滑桩将滑坡推力传递到下部稳定的土层中,依靠土体自身的抗力抵抗滑坡推力.支挡型边坡安全评价指标体系如表2所示.

表2 支挡型黄土高陡边坡安全评价指标体系
3 工程实例分析
3.1 工程背景
包茂高速G65W陕西境黄陵至延安高速公路所处地区由于其地形属黄土高山峻岭,塬面坡度较陡,容易发生滑坡等灾害,且多处黄土塬已经成为黄土岭,两侧滑坡现象很严重,此处高陡边坡综合坡率在1∶1.07~1∶1.42之间,100 m以上的边坡有6个.本文选取最大高度的万花边坡,采用提出的证据推理方法进行安全评价,标段为LJ-19,属于旧滑坡,边坡级数为15级,抗滑桩长度40 m,其余参数如表3所示.万花边坡及其地质剖面图如图1所示.

(a) 万花边坡
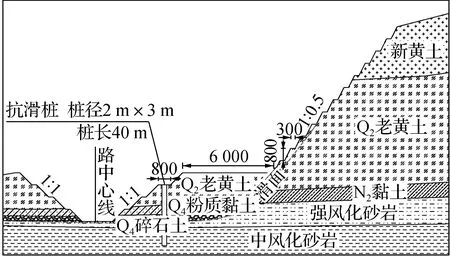
(b) 地质剖面图(单位:cm)

表3 目标边坡参数
本文通过室内试验、现场试验以及现场监测等方法获得基本指标的取值,建立支挡型黄土高陡边坡安全评价指标框架体系,结果如表4和表5所示.位移采用固定式测斜仪进行监测,利用自动采集系统进行数据采集,本文取最大位移作为区间划分依据.

表4 目标边坡土体物理力学参数表
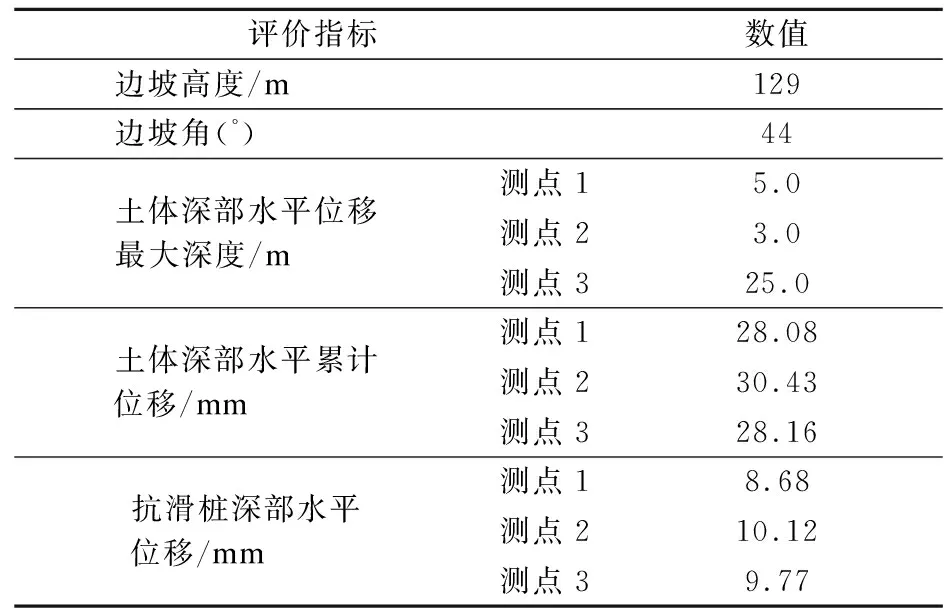
表5 目标边坡指标实测值
3.2 安全评价指标区间划分
以降雨量为例,确定降雨量指标区间划分过程.利用野外设置的降雨测量仪对降雨情况进行监测,利用在边坡上设置的孔隙水压力传感器对边坡土壤进行检测.水平位移与累计降雨量关系如图2所示,由图可知,黄土斜坡土体内部位移随降雨量的增加逐渐增大.土体位移与入渗深度的关系如图3所示,0.4 m深度处土体的位移较大,并呈现出明显的阶段性特点,且试验过程中该部分土体发生了明显的滑移现象.因此,以0.4 m深度处土体位移的变化趋势确定累计降雨量的区间限值.
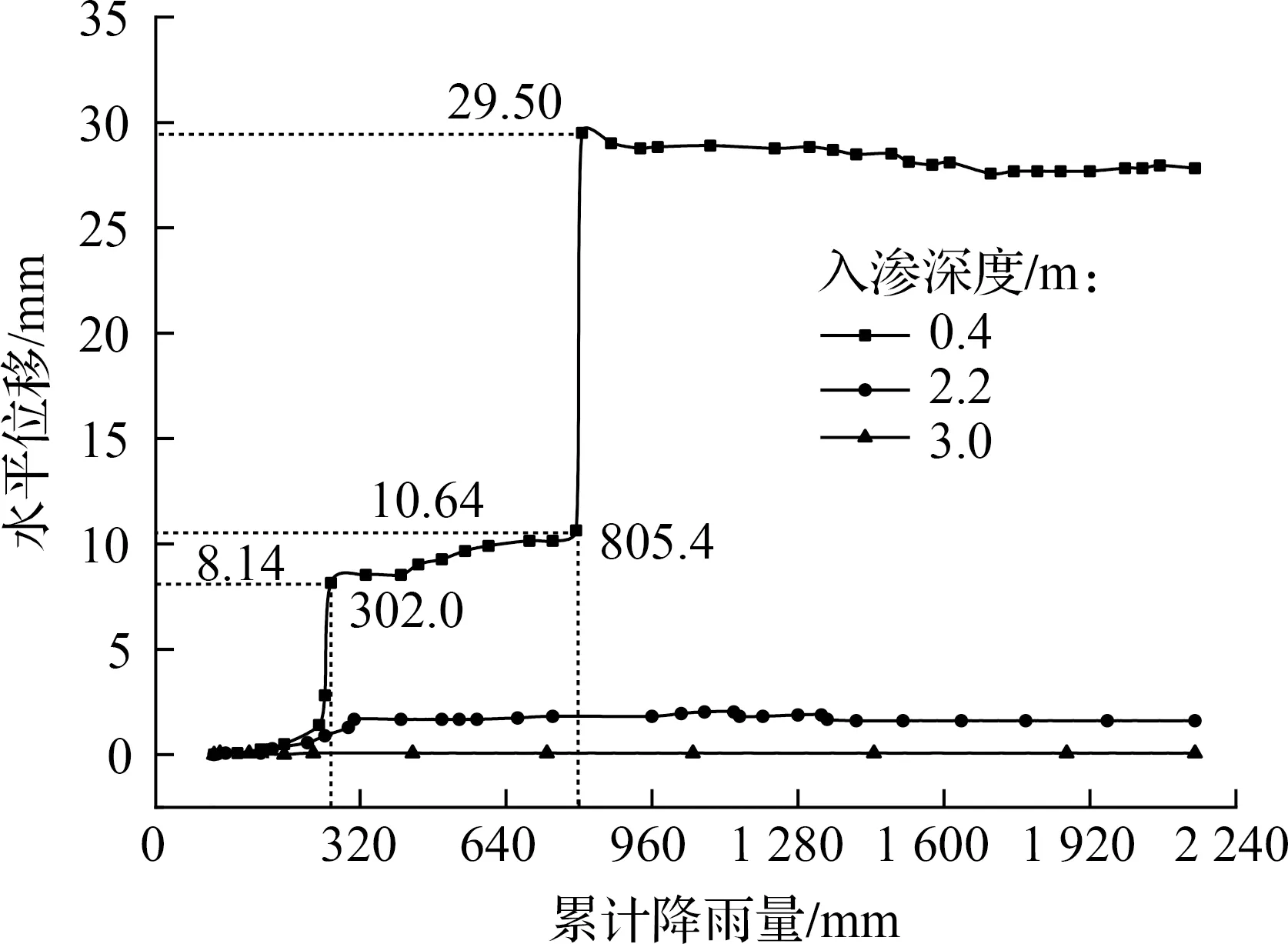
图2 水平位移与累计降雨量关系曲线图
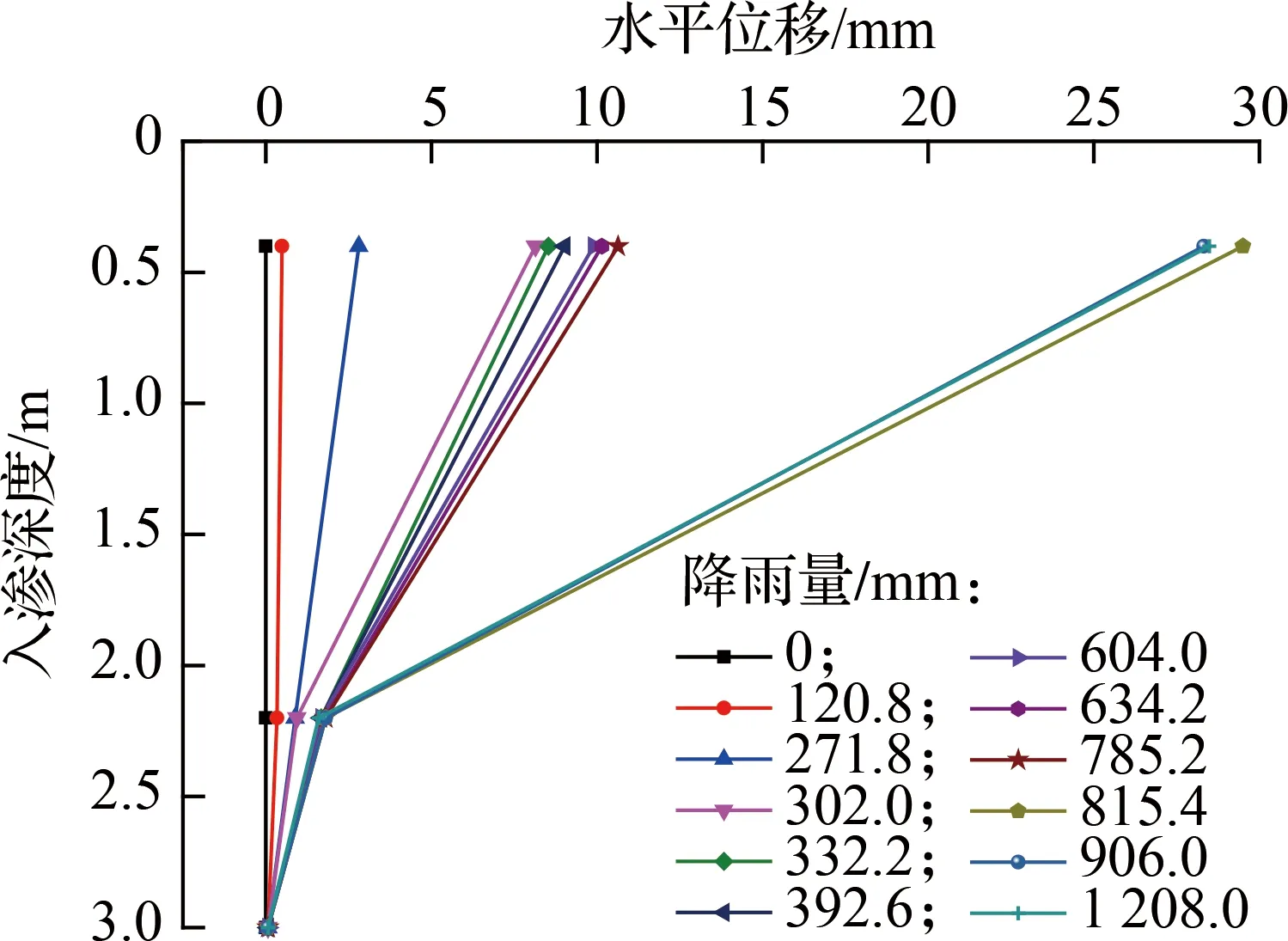
图3 水平位移与入渗深度关系曲线
在30.2 mm/h的降雨强度作用下,0.4 m深度处土体发生滑移,土体位移随降雨量的变化明显分为4个阶段:① 第1阶段,累计降雨量从0增加至120.8 mm,土体位移基本保持不变.②第2阶段,累计降雨量从120.8 mm增加至271.8 mm,土体累计水平位移从0.07 mm增加到1.4 mm,边坡土体位移缓慢增加,但变化量不大.③ 第3阶段,累计降雨量从271.8 mm增加至724.8 mm,当累计降雨量为302 mm时,土体位移由1.40 mm迅速增加至8.14 mm,且随着降雨的持续继续保持缓慢增长,此时该部分土体已经处于不稳定状态.④ 第4阶段,累计降雨量超过724.8 mm,当累计降雨量为815.4 mm时,边坡土体位移由10.64 mm迅速增加至29.50 mm,且随降雨的持续基本保持不变,此时该部分土体已经发生明显的滑移现象.基于以上降雨作用下土体位移随累计降雨量的增加呈现出明显的阶段性的特点,以累计降雨量为指标,将降雨对边坡位移的影响分为4个阶段,得到黄土边坡安全评价等级的标准,如表6所示.

表6 边坡安全评价基本指标区间划分
基于数值模拟以及抗滑桩缩尺模型试验的结果,对土体位移、抗滑桩内力及抗滑桩位移等基本评价指标进行区间划分.土体物理力学特性指标基于室内反复直剪试验和压缩试验的结果进行划分,孔隙水压力和日降雨量根据黄土斜坡人工降雨试验进行划分.具体划分结果如表7所示.

表7 边坡安全评价基本指标区间划分
3.3 各指标基本概率分配
根据图1,利用式(7)、(8)得出各指标各个等级的基本概率分配.由于指标过多,此处以日降雨量为例展示基本概率分配计算过程.①确定区间模型.根据表7,评价指标日降雨量区间数为[0,120]、[120,271]、[271,725]、[725,1500]mm.② 确定识别区间.通过现场监测得到万花边坡某一日的降雨量为29.6 mm,则日降雨量构成的识别区间为[-29.6,29.6]mm.③ 计算区间之间的距离.根据式(7)分别计算辨识框架下的4个区间模型与识别区间之间的距离,计算结果如表8所示.④ 计算区间之间的相似度.根据式(8)分别计算4个区间模型与识别区间之间的相似度,计算结果如表9所示.⑤ 将计算得到的相似度进行归一化处理,得到各辨识框架下的基本概率分配,如表10所示.同理,可计算得到万花边坡其余基本评价指标在辨识框架下的基本概率赋值,计算结果如表11所示.

表8 四种状态下2个区间之间的距离

表9 四种状态下2个区间之间的相似度

表10 四种状态下的基本概率赋值

表11 考虑权重后各指标的基本概率赋值 %
3.4 计算各级指标置信度
采用式(10)计算下级指标作用下上级指标的可信度,计算结果如表12所示.
综合上文基本概率赋值计算,根据相应证据推理的辨识框架,建立了支挡型黄土高陡边坡的安全性评估可信度.从表12可以看出,目标边坡的安全状态和基本安全状态的可靠性分别为73.25%和22.99%,因此可以假定该边坡是安全的,与现场测试结果一致.
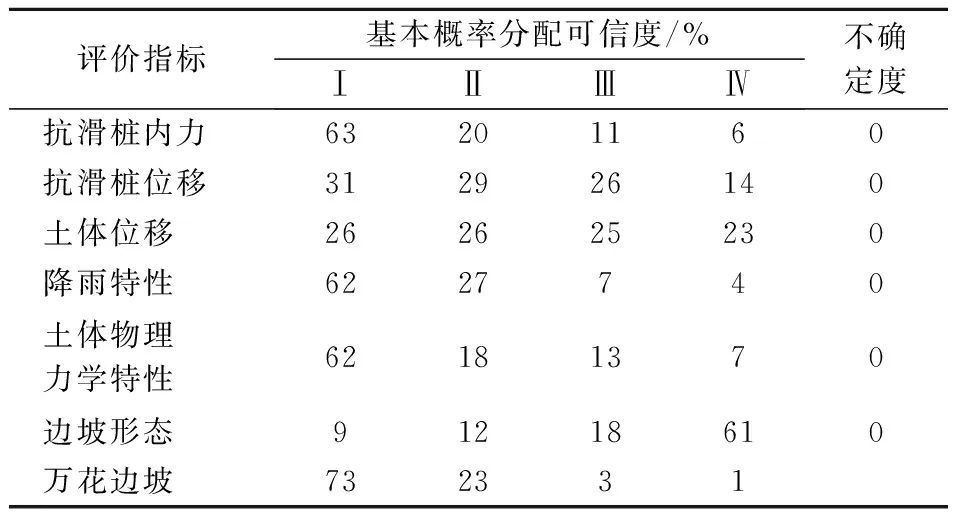
表12 万花边坡基本概率分配可信度
3.5 安全评价结果
各评价指标所占的权重是随现场边坡的实况而动态变化的,由此可对目标边坡稳定性进行动态评估,0~800 d是连续监测的,为方便计算,每10 d取一组数据,利用Python编制计算程序,对其进行迭代运算.在4种稳定级别下,目标边坡坡体及抗滑桩可靠性如图4所示.从图4(a)可看出,抗滑桩在基本安全状态下的可靠度是逐步增加的,由此可以得出抗滑桩是安全的.从图4(b)可看出,60 d时边坡处于基本安全状态的可信度超过了安全状态的可信度,表明从此时起,边坡的安全状态已基本稳定,临界的可信度逐步提高,520 d时坡体在临界状态下的可信度最高,表明土坡的安全状况已达到一个危险的临界状态,并且正在逐渐地向破坏转变.由图4(c)知,目标边坡的安全状况与抗滑桩的可靠性是一致的,目前边坡在安全状态下的概率为73.31%,其安全状况主要依赖于抗滑桩的安全状况.
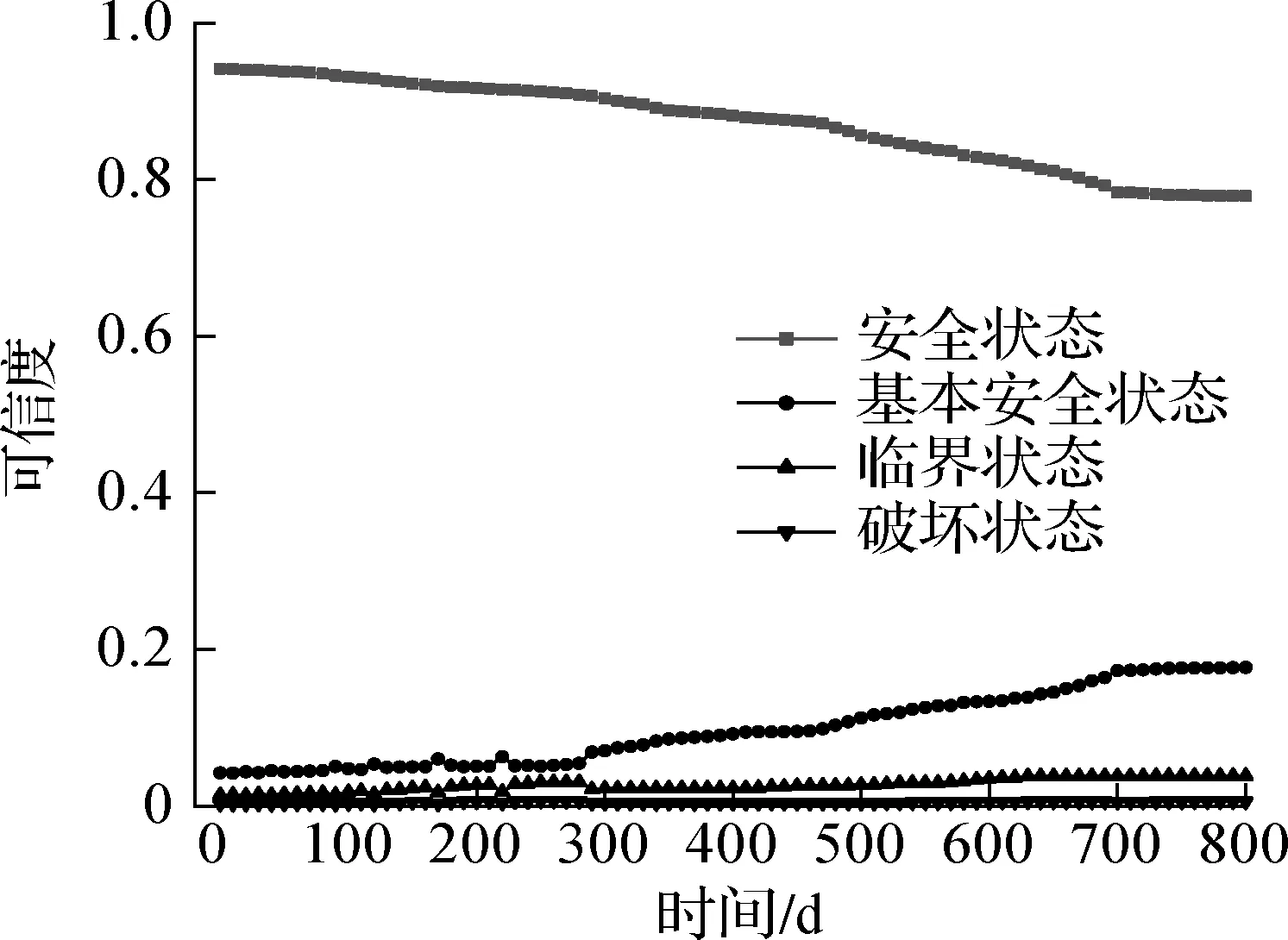
(a) 抗滑桩
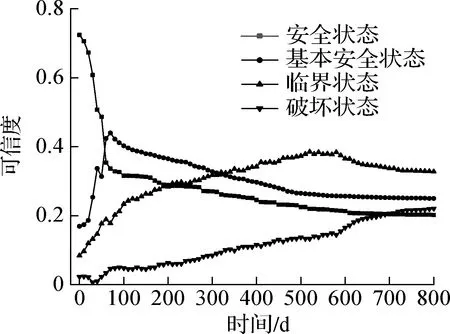
(b) 边坡坡体
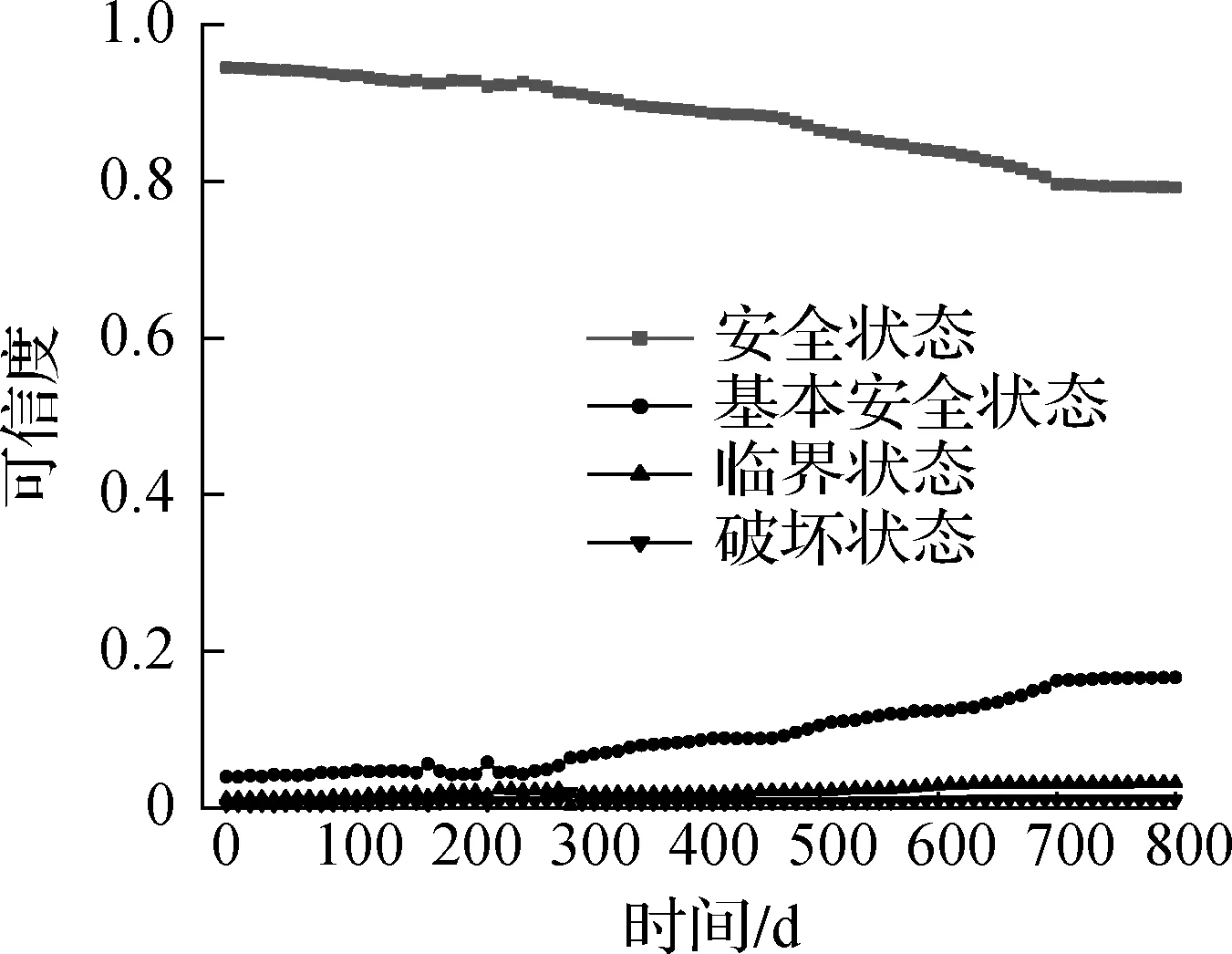
(c) 支挡型边坡整体
边坡动态指标如抗剪强度、降雨量、径排条件、边坡形态、边坡坡度等在边坡位移变化过程中的变化规律如图5所示.由图可知,边坡的安全性变差主要是由于边坡土体内部产生的剪应力达到了边坡土体的抗剪强度;降雨对边坡安全状态的支持程度是随降雨量而变化的,当有降雨产生时,基本指标降雨量对边坡安全状态的支持程度变小,当没有降雨时,降雨量对边坡安全状态的支持程度较大;径排条件、边坡形态与边坡坡度等指标对边坡安全状态的支持程度逐渐降低,并在降雨期间降低得更快.
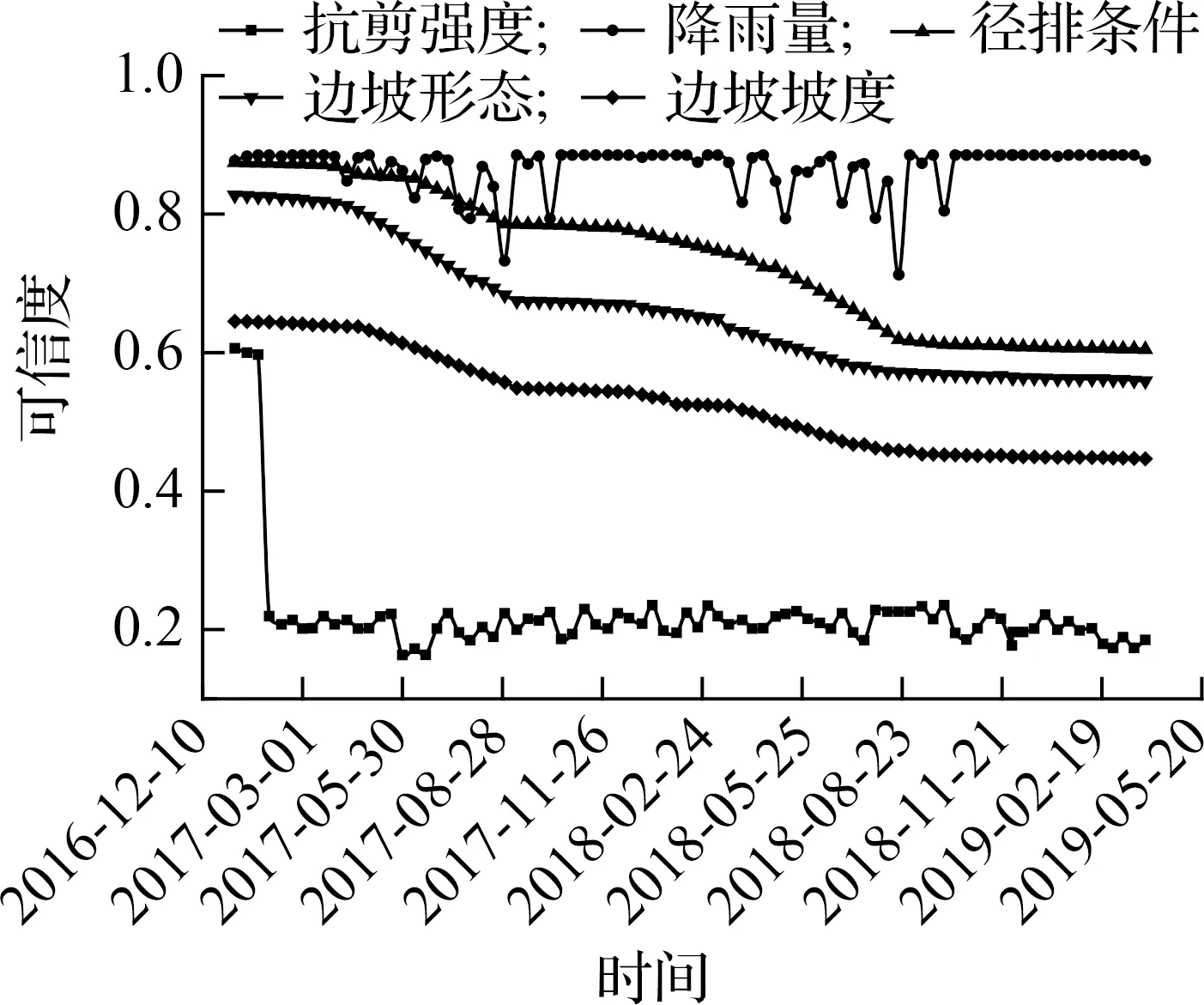
图5 万花边坡动态指标变化规律
4 结论
1) D-S证据理论在边坡稳定性评价的模糊性与不确定性中有优势,可以很好地融合各个指标之间的不一致性,并对各个指标之间的一致性和冲突进行定量衡量,确保各指标能够真实地反映高陡边坡的特征,基于此提出一种支挡型黄土高陡边坡稳定性评价方法.
2) 通过工程实例,对支挡型高陡黄土边坡进行了安全性评估,证实基于证据理论评价的有效性和合理性.通用区间数法来构造基本概率分配的过程合理,且操作性强,计算得出的可信度高,评价结果精确.
3) 用证据理论对边坡安全评价是可行的,且易于用程序实现,通过高陡边坡水平位移推断边坡内部各指标,通过对坡体累积水平位移的现场监测数据推断出抗滑桩的内力指标,从而推导出边坡位移的动态参数.

