正交异性钢-混凝土组合板负弯矩区抗弯性能分析

李 卓 陈玉立,2 单玉麟,2 宗周红,2 许有胜

(1东南大学爆炸安全防护教育部工程研究中心, 南京 211189)

(2东南大学土木工程学院, 南京 211189)

(3深圳市市政设计研究院有限公司, 深圳 518029)

正交异性钢-混凝土组合桥面板是由正交异性钢板与钢筋混凝土通过栓钉或者开孔钢板(PBL)等剪力连接件连接组合而成的.与传统的混凝土桥面板相比,组合桥面板具有更强的刚度和承载力,能够实现更大的跨越.与正交异性钢桥面板相比,钢-混凝土组合桥面板能够有效降低钢桥面的疲劳应力幅,减缓正交异性钢桥面板的疲劳开裂.

Koichi[1]研究了不同连接程度的钢-混凝土组合板,得到用于分析不完全连接组合板钢板厚度的偏微分方程.Nie等[2-3]通过试验发现钢-混组合华夫板具有良好的延性和较高的承载力.杨悦等[4]利用受弯试验得到钢板-混凝土组合板受弯的3种破坏形态,提出了相应的受弯承载力公式.徐宙元[5]试验研究了平钢板-混凝土组合单向板正负弯矩区的抗弯性能.Sharmila[6]通过静载试验分析了不同连接件对平钢板-混凝土组合板受力性能的影响.Su等[7-9]采用负弯矩加载试验,研究了正交异性钢-混凝土组合板负弯矩区受力性能.为解决组合板负弯矩区混凝土开裂问题,聂建国等[10]提出了抗拔不抗剪连接新技术.Shao等[11-12]通过数值模拟案例分析得到,超高性能混凝土(UHPC)层的加入可明显改善正交异性钢桥面板的疲劳开裂问题.廖子南等[13]进行负弯矩受弯试验和有限元分析发现,相较于普通钢-混凝土组合板,钢-UHPC组合板在负弯矩作用下具有更好的延性.Xiao等[14]开展了平钢板-UHPC连续板的抗弯性能试验及数值模拟.Bu等[15]进行了正交异性钢板-UHPC组合板负弯矩区抗弯性能试验及分析研究.邱景雷[16]通过静载试验,研究了带PBL剪力连接件的平钢板-混凝土组合板的破坏模式及其负弯矩区力学性能.曾明根等[17]基于两点静载试验,分析了带有钢纤维的混凝土组合板的开裂弯矩与极限弯矩.

正交异性钢-混凝土组合板能大幅提升桥面板的整体刚度,降低钢桥面板疲劳应力幅,减少柔性铺装层发生各类病害乃至破坏的可能性[18-19].目前,针对组合板的研究主要集中于平钢板-混凝土组合板,关于正交异性钢-混凝土组合板的研究则较少.对于组合板而言,由于其负弯矩区混凝土处于受拉区,混凝土的受拉开裂会导致整体结构强度及刚度降低.虽然采用UHPC可以提高混凝土的抗弯强度,但其造价较高,养护施工难度较大,不适合于应用推广.本文通过在普通混凝土中掺加少量钢纤维,研究正交异性钢-混凝土组合板负弯矩区的力学性能.针对1块掺加钢纤维的正交异性钢-混凝土组合简支板、1块正交异性钢-普通混凝土组合连续板和1块正交异性钢-钢纤维混凝土组合连续板进行抗弯试验和数值模拟,对比负弯矩区的开裂荷载和极限承载力.试验结果可为正交异性钢-普通钢筋混凝土组合板的设计及工程应用提供借鉴.

1 试验

1.1 试件设计

本文以某斜拉桥为背景,以该桥上正交异性钢-混凝土组合桥面板为原型,按照缩尺模型与原型尺寸比例1∶2进行缩尺试验.原型桥面板单跨长4 400 mm,宽3 600 mm,混凝土板厚160 mm,钢板厚16 mm.设计了1块正交异性钢-混凝土组合简支板(编号为OCSN1)和2块正交异性钢-混凝土组合连续板(编号为OCSC1和OCSC2).其中,试件 OCSN1中钢纤维分布在整个混凝土板层,试件OCSC1中钢纤维分布在支座负弯矩区混凝土层,试件OCSC2则为普通混凝土的组合板.组合简支板长2 350 mm,宽1 800 mm,高238 mm.2块组合连续板尺寸相同,长4 400 mm,宽1 800 mm,高238 mm.混凝土层与底钢板通过开孔钢板连接件连接.正交异性钢板和开孔钢板均采用Q355钢材,开孔钢板厚6 mm,高60 mm,长度与板长一致,开孔直径为35 mm,开孔中心间距为125 mm.正交异性钢顶板厚8 mm,U形加劲肋尺寸为225 mm×150 mm×4 mm,钢板加劲肋厚10 mm,横梁厚14 mm.混凝土等级为C60,混凝土层厚80 mm,混凝土内分布钢筋和贯穿钢筋型号均为HRB400,直径均为10 mm.表1为组合板试件尺寸参数表;图1为正交异性钢-混凝土组合板尺寸图.

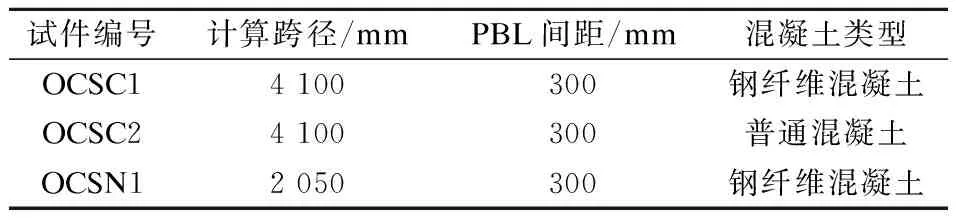
表1 试件尺寸参数

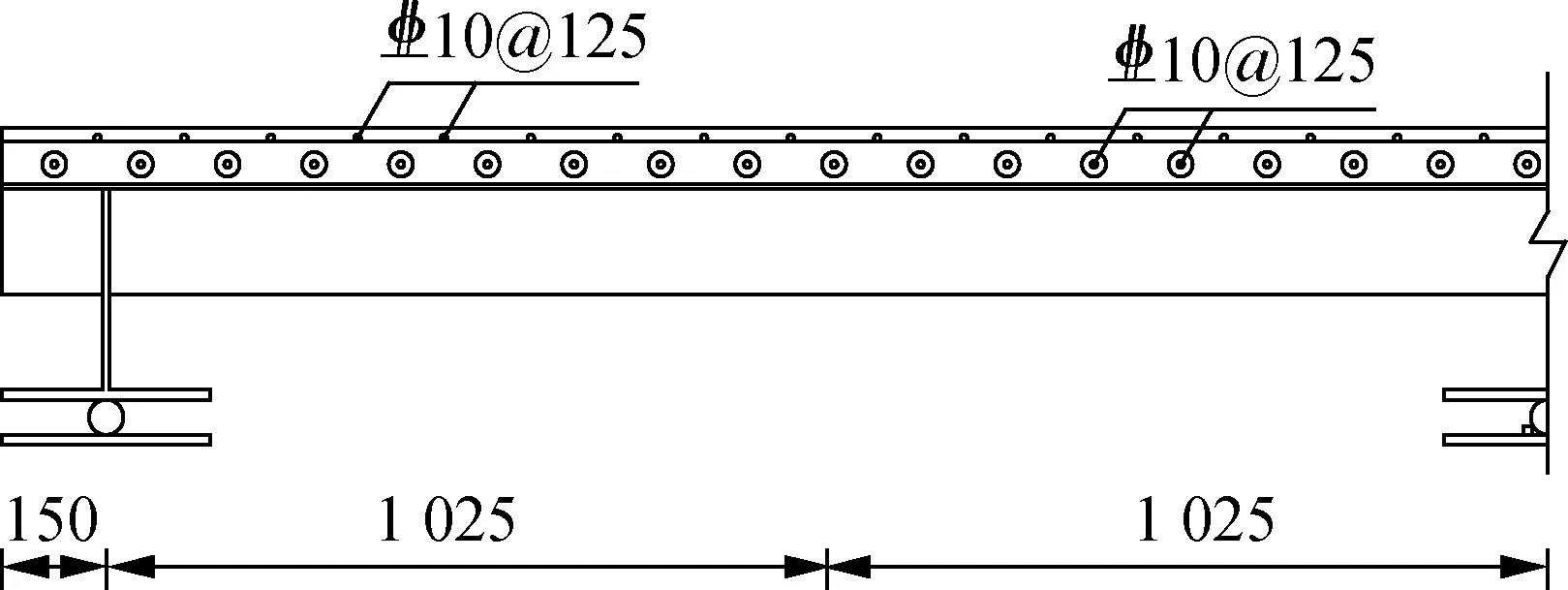
(a) 组合连续板立面图

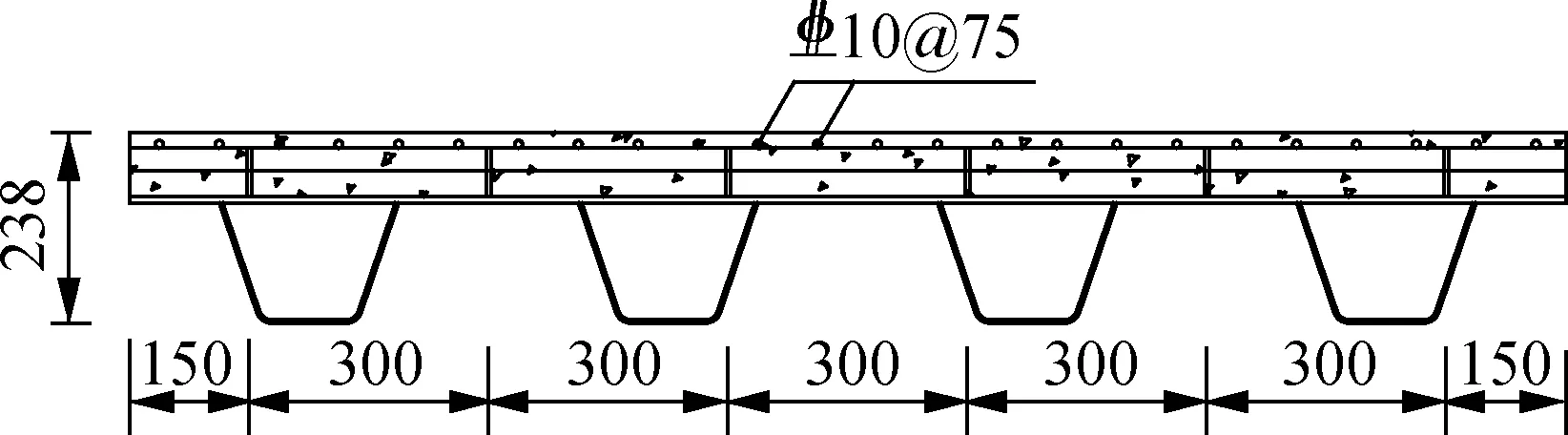
(b) 组合连续板横截面图

(c) 组合连续板钢纤维分布

(d) 开孔钢板连接件尺寸

1.2 加载方案及测点布置

本试验主要研究正交异性钢-混凝土组合板负弯矩区的受力性能.简支板采用跨中单点反向加载,将混凝土作为受拉区域,正交异性钢板作为受压区域.约束条件为在一端混凝土板下使用固定钢滚轴作为固定铰支座,另一端使用可滚动的钢滚轴作为滑动铰支座.连续板采用跨中两点对称加载,中支座使用固定钢滚轴作为固定铰支座,两端则使用可动钢滚轴作为滑动铰支座.加载示意图见图2.

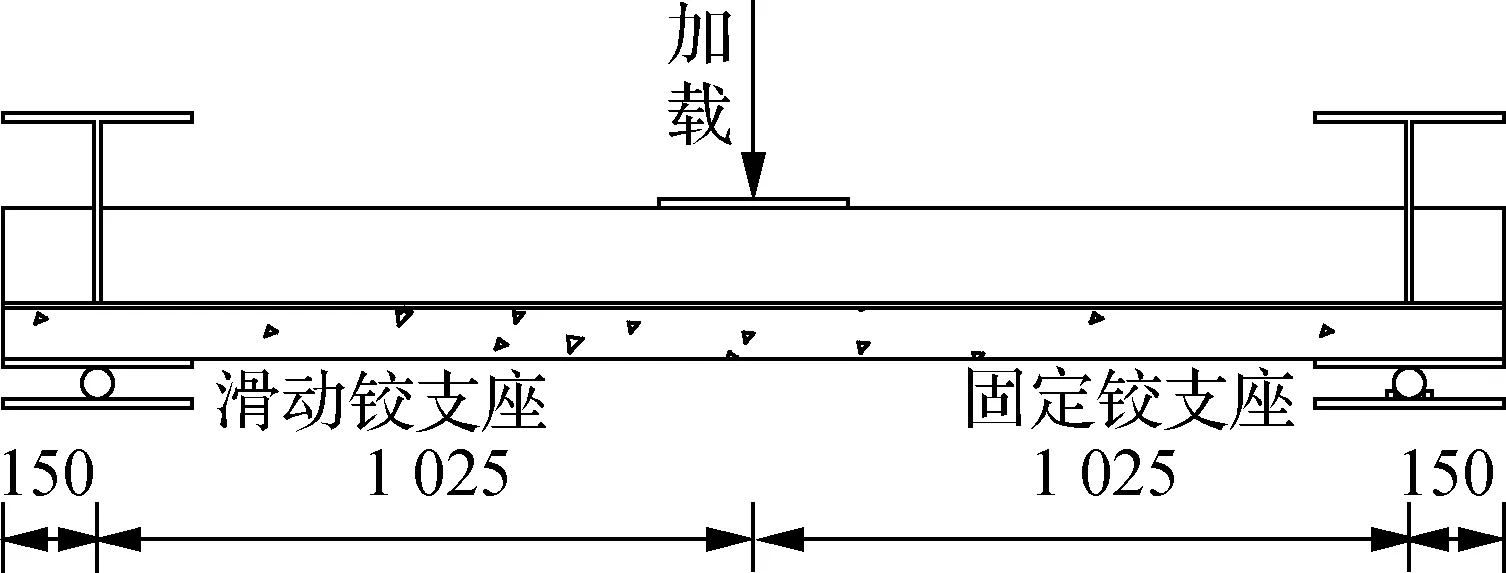
(a) 组合简支板加载示意图

(b) 组合连续板加载示意图

(c) 组合简支板加载照片

(d) 组合连续板加载照片

采用MTS液压加载系统对组合板进行单调静力加载.正式加载前,对试验板采用0～20 kN分级加载的方式,并循环3次,使试件各部分接触良好,进入工作状态.正式加载时,前期以每级20 kN的力增量进行加载控制,记录相应位移和钢板应变,直到钢板出现屈服或者简支板混凝土出现开裂.然后,以每级1 mm的位移增量进行加载控制,直至试件发生破坏或荷载呈现下降趋势,记录相应荷载.

测试内容包括组合板加载点截面处混凝土和钢板的纵向应变以及加载点位置的竖向位移、连续板负弯矩区混凝土和钢板的纵向应变及裂缝发展分布情况.图3为组合连续板的测点布置.轴作为固定铰支座,另一端使用可滚动的钢滚轴作为滑动铰支座.连续板采用跨中两点对称加载,中支座使用固定钢滚轴作为固定铰支座,两端则使用可动钢滚轴作为滑动铰支座.加载示意图见图2.

(a) 立面图

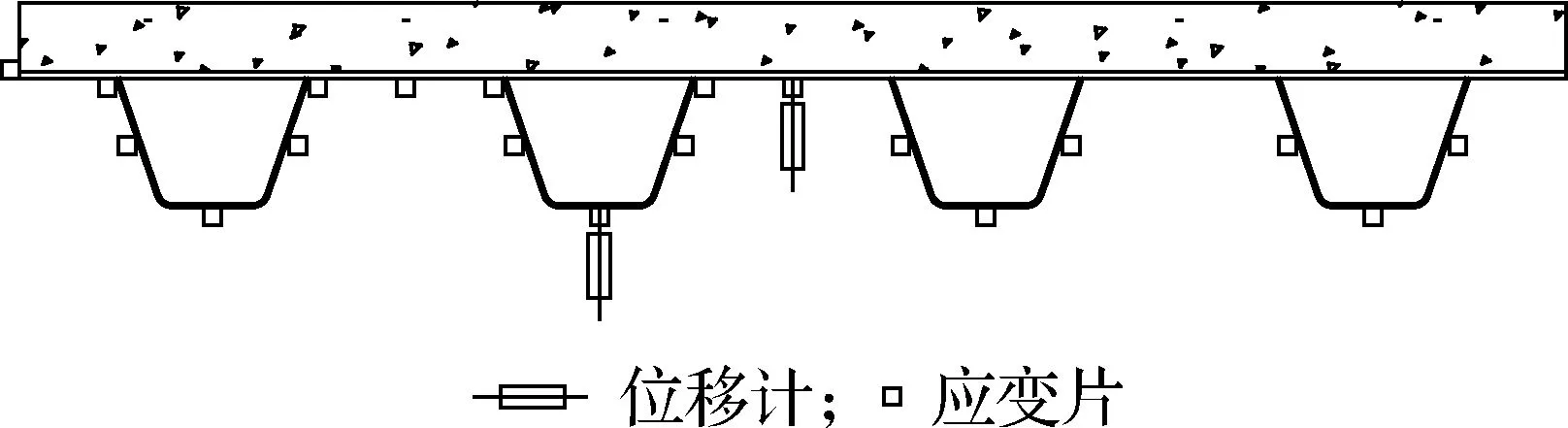
(b) 横截面图

2 试验现象与结果分析

2.1 破坏形态

试验中,观察并记录施加静载的正交异性钢-混凝土组合板的混凝土板初始裂缝出现时间、裂缝发展情况及钢板屈曲现象和最终破坏模式.

对于试件OCSN1,当作动器荷载为100 kN时,混凝土板跨中加载位置处横向两侧各出现1条竖向裂缝,初始裂缝宽度为0.05 mm.当作动器荷载为120 kN时,竖向裂缝发展并于混凝土顶板上形成横向贯穿裂缝,贯穿裂缝宽度为0.1 mm,之后转为位移控制加载.随着荷载的持续增加,裂缝数量也增加.当作动器荷载为479.9 kN时,试件达到极限状态,停止加载,此时混凝土顶板出现多条贯穿裂缝,最大裂缝宽度为0.2 mm,混凝土受拉退出工作,加载点下处U肋出现受压局部屈曲现象.组合简支板加载破坏形态和裂缝分布见图4.

(a) 跨中混凝土板开裂

(b) 跨中钢板U肋屈服

对于试件OCSC1,当作动器荷载为120 kN时,中间支座的混凝土板横向两侧面出现初始竖向裂缝,裂缝宽度为0.05 mm.当荷载为781.3 kN时,竖向裂缝发展并于混凝土顶板上形成贯穿裂缝,裂缝宽度为0.2 mm.当作动器荷载为1 278.6 kN时,组合板出现巨大响声,中间支座处的钢板U肋出现屈曲现象.当荷载达到1 620.9 kN时,组合板支座位置至加载点间出现斜向大裂缝,组合板一跨存在明显弯曲,中间支座附近受拉混凝土退出工作,受压U肋出现局部屈曲现象;加载点处混凝土局部压碎,受拉U肋屈服,中间支座形成塑形铰,试件发生大变形破坏,最大裂缝宽度为0.65 mm.试件OCSC1的破坏形态及裂缝分布见图5.

(a) 支座混凝土板开裂

试件OCSC2的开裂和破坏现象与试件OCSC1基本类似.试件OCSC2的开裂荷载为100 kN,初始裂缝宽度为0.05 mm;贯穿裂缝荷载为280 kN,贯穿裂缝宽度为0.1 mm;当荷载达到1 267.6 kN时,中支座位置观察到U肋局部屈曲现象.试件OCSC2的极限荷载为1 609.4 kN,加载点下混凝土压碎破坏,受拉最大裂缝宽度为0.6 mm.

2.2 结果分析

表2给出了正交异性钢-混凝土组合板的主要试验结果.表中,Pcr为开裂荷载;Py、δy分别为屈服荷载及其对应的挠度值;Pu、δu分别为极限荷载及其对应的挠度值.

表2 试件主要试验结果

2.2.1 荷载-挠度曲线

图6给出了试件OCSN1在跨中单点反向加载作用下的荷载-挠度曲线.由图可知,对于组合简支板,荷载-挠度曲线可近似分为弹性、弹塑性和塑性3个阶段.在弹性阶段,荷载和挠度为线性关系,荷载-挠度曲线呈上升趋势,跨中混凝土底板未出现裂缝,组合板刚度由混凝土和正交异性钢板共同提供.在弹塑性阶段,荷载-挠度曲线斜率逐渐下降,混凝土底板出现开裂并迅速贯穿,最终跨中混凝土底板出现多条贯穿裂缝,部分混凝土底板退出工作,组合板刚度主要由正交异性钢板提供.在塑性阶段,组合简支板荷载-挠度曲线陡然下降,正交异性钢板屈曲,随着荷载的增加,正交异性钢板达到极限强度,组合简支板发生破坏.

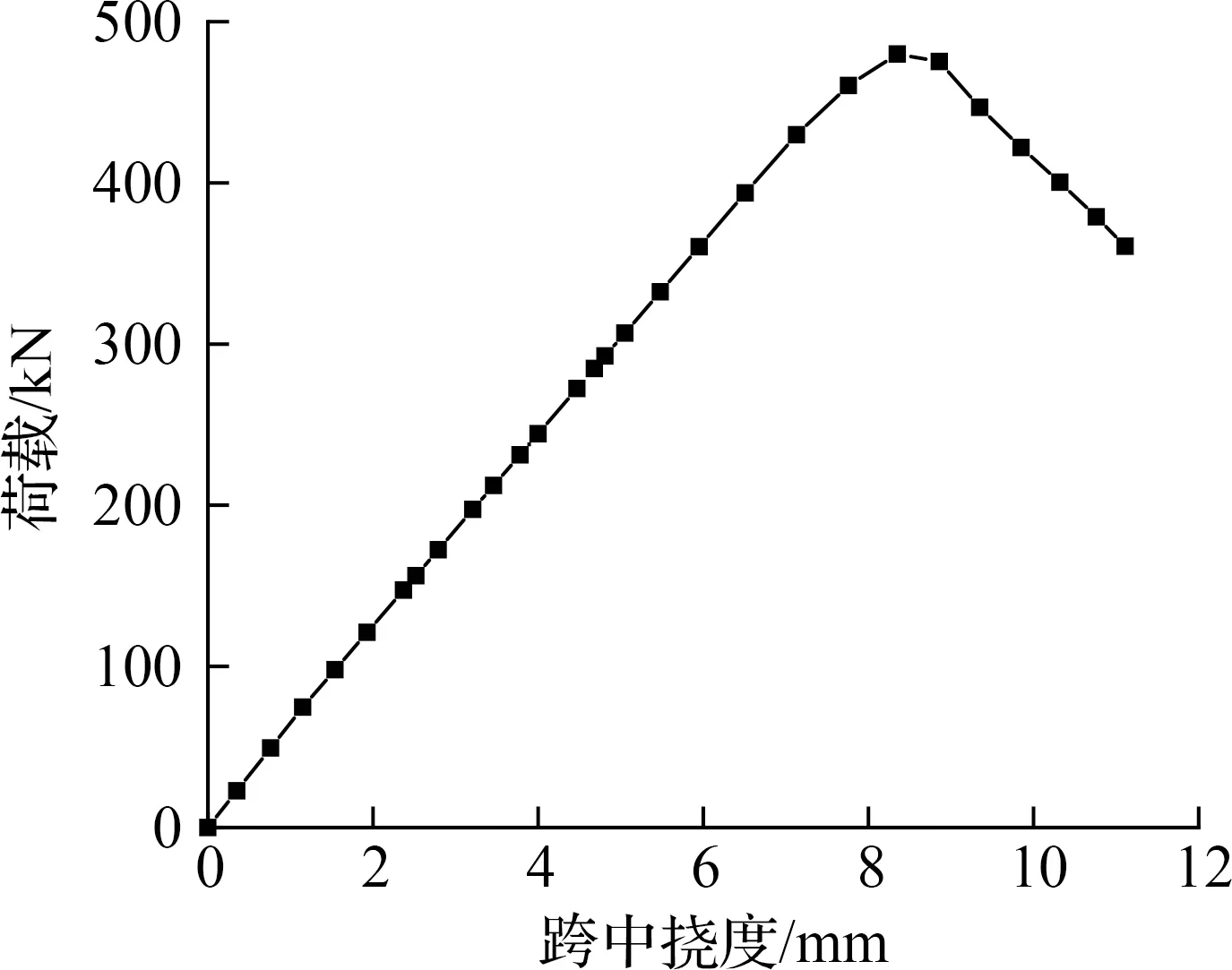
图6 试件OCSN1的荷载-挠度曲线

图7给出了试件OCSC1和试件OCSC2在跨中两点加载作用下的荷载-挠度曲线.由图可知,对于组合连续板,荷载-挠度曲线可近似分为弹性、弹塑性和塑性3个阶段.在弹性阶段,荷载和挠度呈线性关系,正交异性钢板与混凝土板共同工作,组合板全截面未出现混凝土开裂或钢板屈服.在弹塑性阶段,荷载-挠度曲线斜率逐渐下降,组合连续板中间支座负弯矩区混凝土开裂,混凝土纵向两侧竖向裂缝向混凝土顶板发展并贯穿,裂缝数量不断增加,组合连续板刚度下降,最终中间支座位置附近的U肋发生局部屈曲,中间支座形成塑性铰.在塑性阶段,组合连续板荷载-挠度曲线斜率平稳,曲线呈下降趋势,组合连续板整体屈服,此时跨中位置处U肋发生屈曲,跨中挠度随荷载增大而迅速增大,跨中位置混凝土出现裂缝,最终跨中混凝土顶板被压碎,正交异性钢板U肋屈服,组合连续板发生破坏.

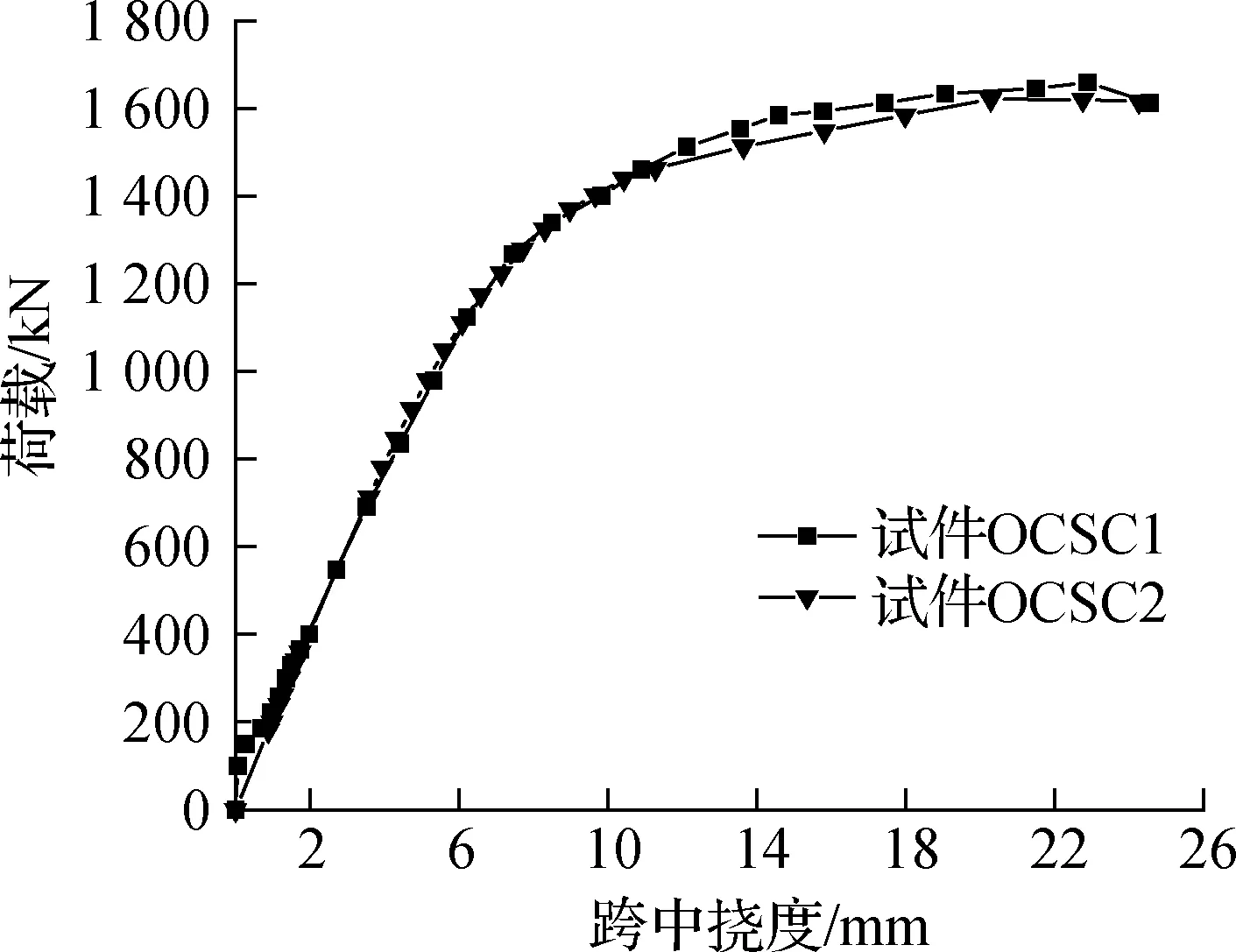
图7 试件OCSC1和OCSC2荷载-挠度曲线

试件OCSC1和试件OCSC2两条荷载-挠度曲线基本重合.这是因为2块组合连续板的极限承载力仅与其跨中截面有关,其跨中截面相同,故极限承载力大致相同.

2.2.2 荷载-应变曲线

图8给出了正交异性钢-混凝土组合板负弯矩区应变沿截面高度的分布及变化趋势.以正交异性钢板U肋底面到混凝土板顶面距离作为截面高度.

(a) 试件OCSN1跨中截面

(b) 试件OCSC1支座截面

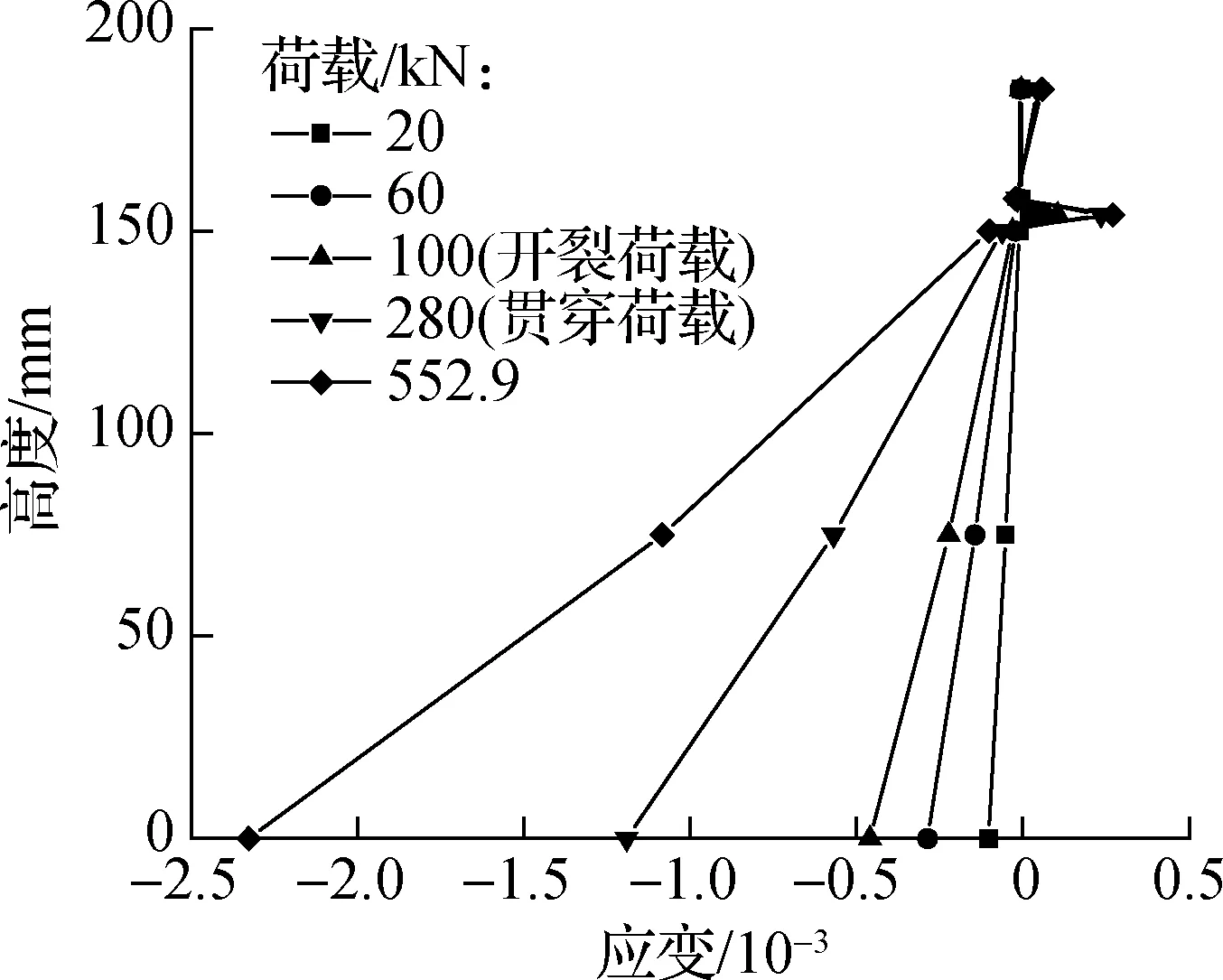
(c) 试件OCSC2支座截面

通过组合简支板和组合连续板的负弯矩区截面应变分布可以看出,在混凝土开裂前,截面应变近似呈直线分布,基本符合平截面假定.而当混凝土开裂后,截面应变则呈现不规律分布,不再符合平截面假定.

由图8可知,组合板应变在钢混交界面处(截面高度150 mm处)出现较大变化.究其原因在于,施加荷载过程中,钢与混凝土交界面存在滑移现象,故在钢混交界面处混凝土和钢板的应变会出现差异.以试件OCSN1为例,当混凝土裂缝贯穿之后,钢板和混凝土分开工作,使得混凝土在负弯矩区顶板受拉、底板受压,钢板顶部受拉、底部受压,反映在应变分布图上即为2种材料顶部均为正应变,底部均为负应变.对比组合连续板与组合简支板的截面应变分布曲线可以看出,交界面处简支板的应变偏移程度较连续板更大,说明在静载作用下组合简支板钢混界面滑移程度较组合连续板更大.

组合板负弯矩区U肋底板荷载-应变曲线见图9.由图可见,在组合板达到屈服荷载之前,压应变与荷载基本呈线性关系.加载至屈服荷载时,U肋底板达到屈服状态.

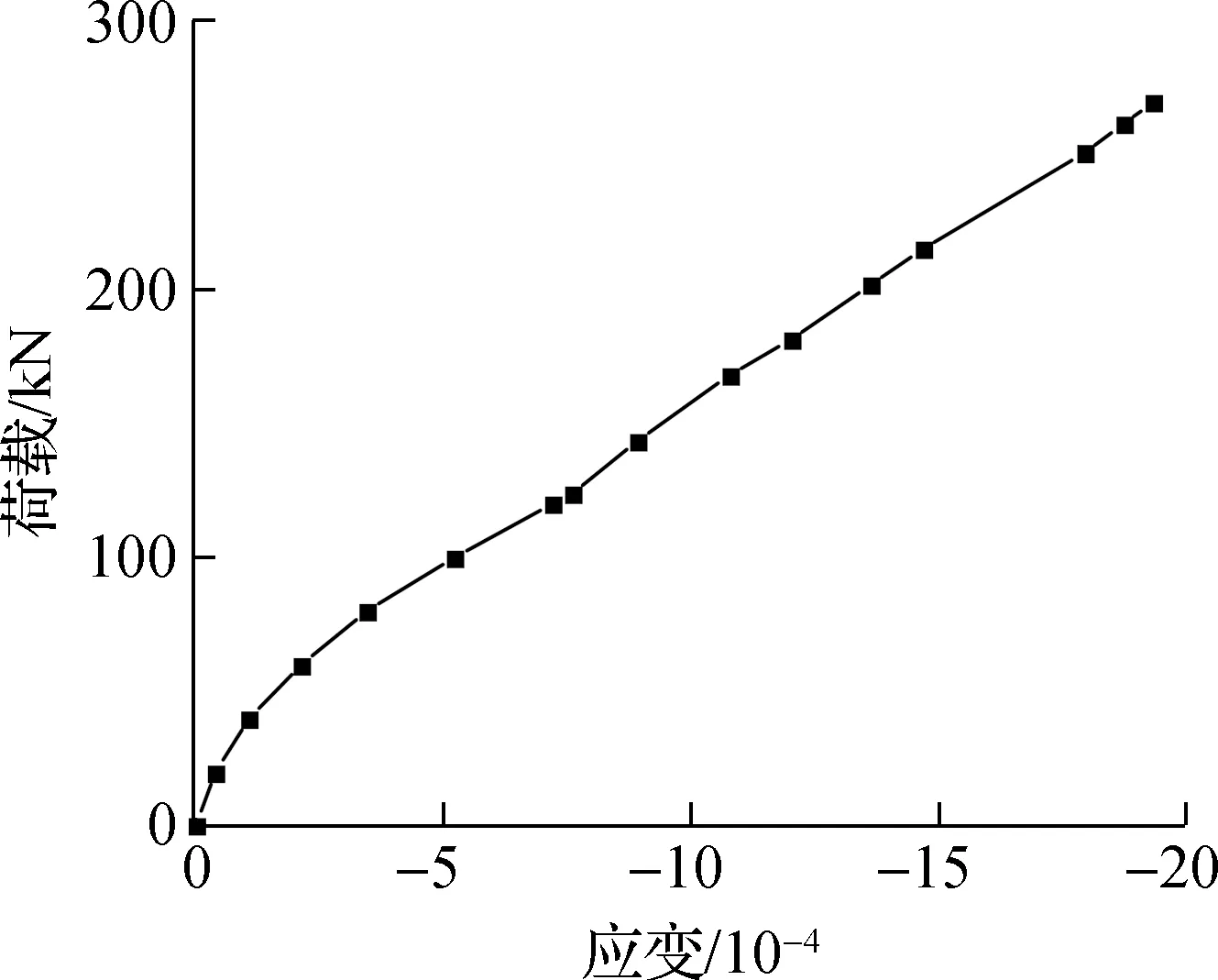
(a) 试件OCSN1跨中U肋

(b) 试件OCSC1支座U肋

(c) 试件OCSC2支座U肋

2.2.3 裂缝分布

图10给出了试件OCSC1和OCSC2的裂缝情况对比.受钢纤维阻碍裂缝发展影响,达到相同宽度的初始裂缝和贯穿裂缝时,试件OCSC1所能承受的荷载比试件OCSC2更大,且试件OCSC1的延性也更优.

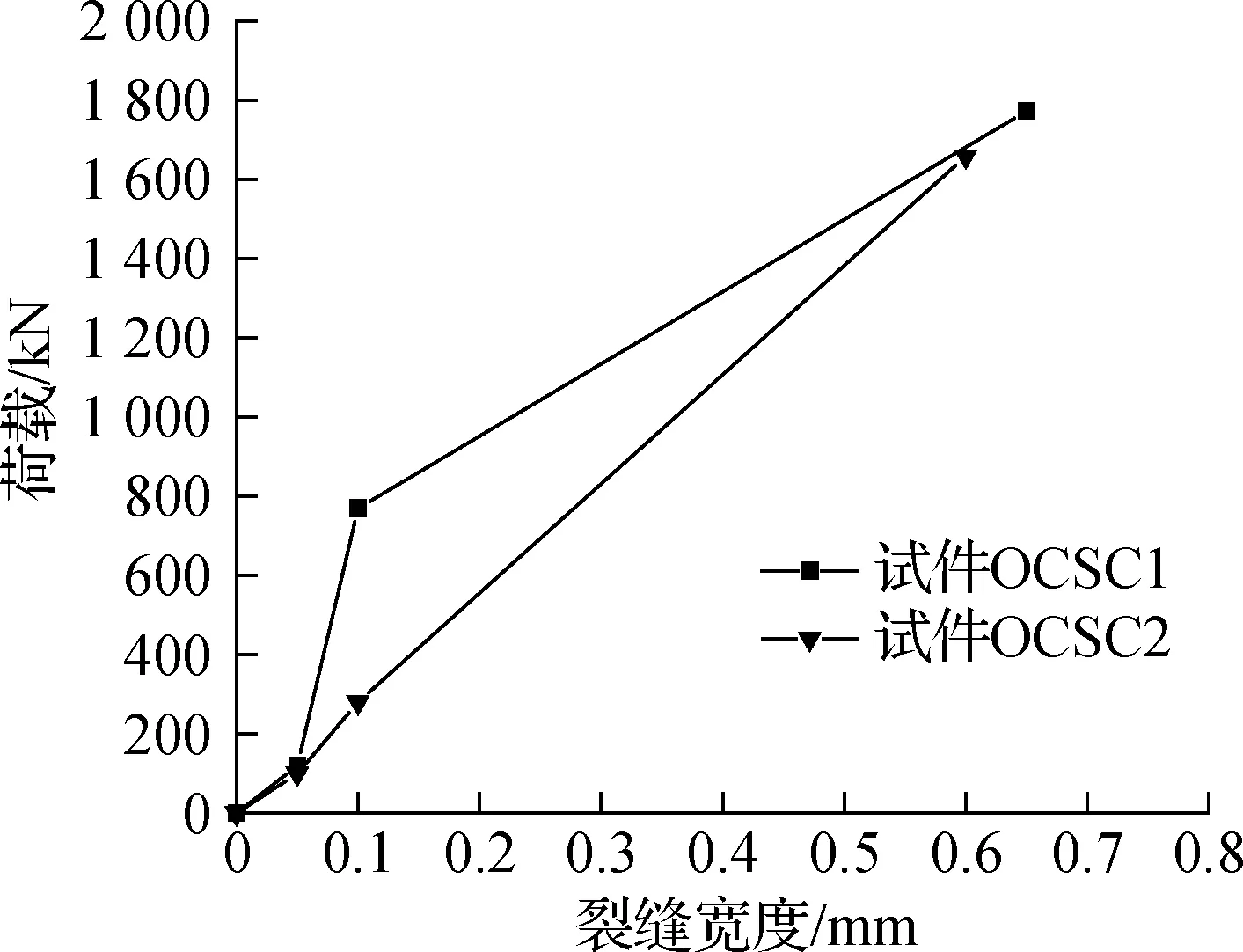
图10 试件OCSC1和OCSC2裂缝情况对比

表3给出了3个试件的初始裂缝宽度S0、贯穿裂缝宽度S1、最大裂缝宽度Sm及其对应的荷载P0、P1、Pm.

表3 不同试件裂缝宽度及对应荷载

3 组合板非线性分析

3.1 有限元模型

本文采用有限元软件ABAQUS对3块试验板进行非线性分析.正交异性钢板包括钢顶板、U肋、腹板、加劲肋及横梁,使用四节点三维壳单元S4R;混凝土层及PBL开孔钢板连接件使用八节点三维实体单元C3D8R;贯穿钢筋和分布钢筋使用两节点三维桁架单元T3D2.考虑到模型计算精度与计算效率,网格划分采用25 mm×25 mm的网格尺寸.组合简支板采用单点反向加载,在正交异性钢板U肋上设置钢垫板,加载点设置在钢垫板上,同时支座位置处也设置钢垫板,以防出现应力集中现象.对于组合连续板采用两点对称加载,在跨中加载点处设置钢垫板.对于连续板,将混凝土板区域划分为普通混凝土区和钢纤维混凝土区域.

3.2 材料本构关系

ABAQUS软件中提供了3种混凝土本构模型,即塑性损伤模型、弥散开裂模型和脆性开裂模型.聂建国等[20]认为混凝土结构在承受拉压双向应力时采用塑性损伤模型模拟效果更好,该模型考虑了混凝土在拉压状态下的软化现象.因此,本文也使用塑性损伤模型来模拟混凝土在正负弯矩区的塑性变化.

3.2.1 钢纤维混凝土和普通混凝土

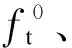
(1)

(2)

(3)

式中,αc1为混凝土棱柱体与立方体抗压强度的比值.据此计算得到的普通混凝土材料的轴心抗压强度、轴心抗拉强度、弹性模量分别为44.2、3.64、35 558 MPa.

对于钢纤维混凝土,单轴本构关系依据池寅等[23]提出的钢-聚丙烯混杂纤维混凝土(HFRC)应力-应变关系拟合公式得到.其中,单轴受压应力-应变关系式为

(4)

式中

(5)

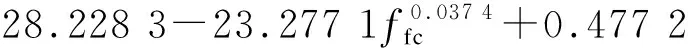
0.491 7λpf

(6)

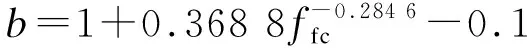
(7)

ffc=fc(1+0.206λsf+0.388λpf)

(8)

εfc0=εc0(1+0.705λsf+0.364λpf)

(9)

式中,σc、εc分别为HFRC单轴受压时的应力和应变;ffc、εfc0分别为HFRC的单轴抗压强度及其峰值应变;fc、εc0分别普通混凝土的单轴抗压强度及其峰值应变;λsf、λpf分别为钢纤维和聚丙乙烯的特征参数,且λsf=Vsf(lsf/dsf),λpf=Vpf(lpf/dpf),其中,Vsf、Vpf分别为钢纤维和聚丙乙烯的体积分数,lsf、lpf分别为钢纤维和聚丙乙烯的长度,dsf、dpf分别为钢纤维和聚丙乙烯的直径.

单轴受拉应力-应变关系式为

σt=(1-dte)Eftεt

(10)

式中

(11)

(12)

α1=1.2(1+0.265λsf+0.277λpf)

(13)

(14)

fft=ft(1+0.379λsf+0.02λsfλpf)

(15)

εft=εt(1+0.498λsf+0.697λpf

(16)

式中,σt、εt分别为HFRC单轴受拉时的应力和应变;Eft、Ef0分别为HFRC和普通混凝土的弹性模量;fft、εft分别为HFRC的单轴抗拉强度及其峰值应变;ft、εt为普通混凝土的单轴抗拉强度及其峰值应变.

根据拟合公式(6)～(9)和(13)～(16)可以看出,聚丙乙烯和钢纤维2种掺杂材料互不影响.本文仅考虑掺加钢纤维的情况,取聚丙乙烯体积分数为0.试验中材料参数选取如下:Vsf=1%,dsf=0.75 mm,lsf=35 mm,ffc=48.5 MPa,fft=4.28 MPa,Eft=36.207 GPa.

3.2.2 钢板和钢筋

Q355钢材及HRB400钢筋采用双折线弹塑性模型,分为弹性段和强化段,不考虑断裂失效(见图11).其中,弹性段的弹性模量为E0,强化段的弹性模量为0.01E0[24],所用材料参数按照材性试验取用,具体材料参数见表4.表中,σs,y、σs,u分别为钢材的屈服强度和极限强度;εs,y、εs,u分别为钢材的屈服应变和极限应变.

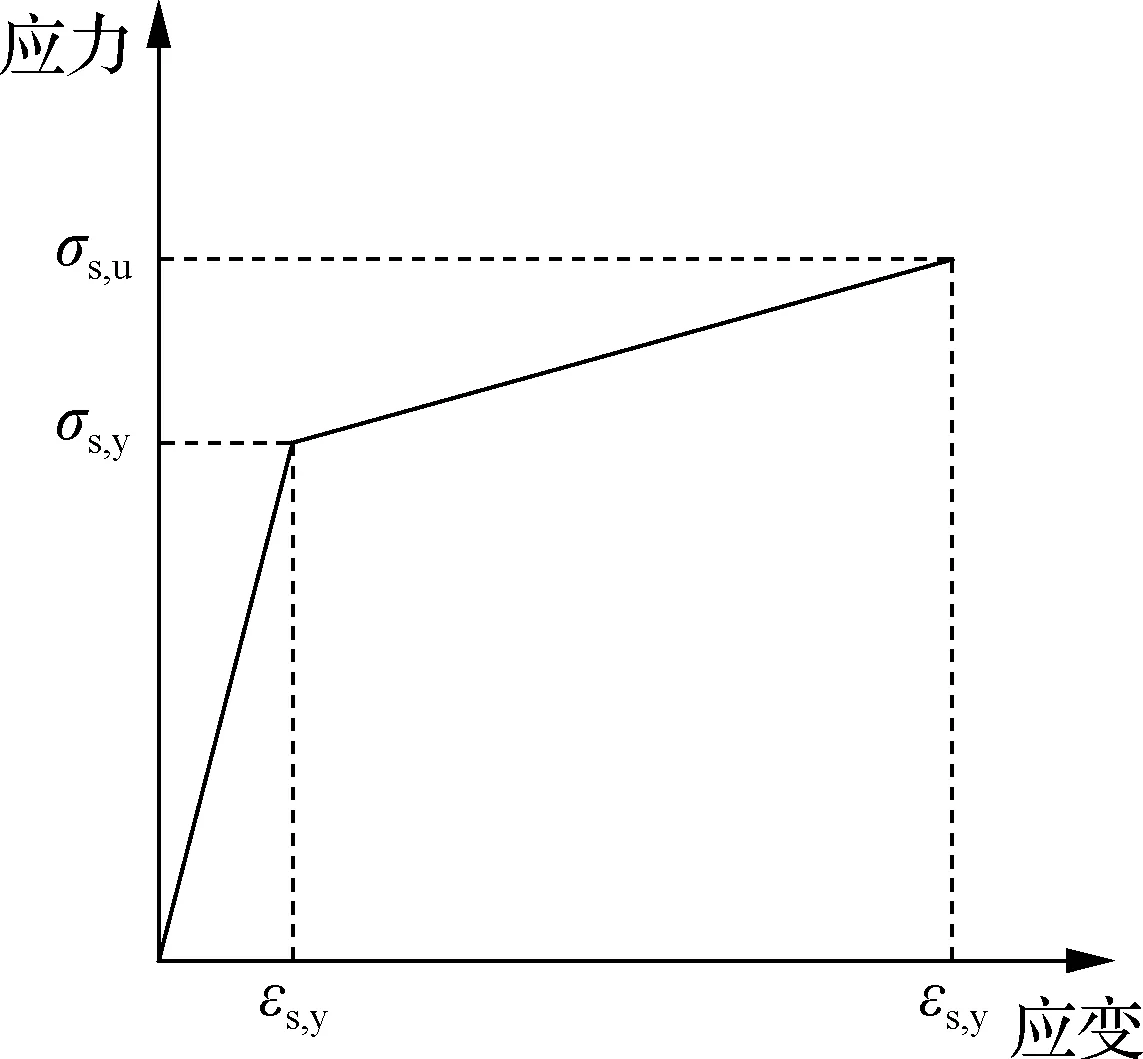
图11 钢材及普通钢筋的应力-应变曲线

表4 钢材及普通钢筋材料参数

3.3 界面相互作用及边界条件模拟

本试验中,混凝土板与底钢板以及混凝土板与开孔钢板间的接触行为采用面与面接触模拟[25];法向接触力采用硬接触模拟;切向接触力采用摩擦系数为0.2的罚摩擦模拟;所有底钢板之间的连接采用共节点的连接方式;开孔连接件与底钢板的连接以及加载钢垫板与组合板的连接采用tie约束模拟;分布钢筋与混凝土间连接采用embedded region约束模拟.

采用线约束来模拟组合板的边界条件.通过在组合板支座一端约束3个方向上的位移来模拟固定铰约束,在另一端约束2个方向上的位移以模拟滑动铰支座.

3.4 有限元模拟结果

采用力和位移加载方式对正交异性钢-混凝土组合板进行非线性全过程分析,提取跨中位置荷载-挠度曲线、钢板U肋底板的荷载-应变曲线以及主要破坏现象与试验结果进行比较.

3.4.1 荷载-挠度曲线对比

有限元模拟得到的跨中荷载-挠度曲线与试验结果对比见图12.由图可知,有限元模拟得到的正交异性钢-混凝土组合板跨中荷载-挠度曲线与试验曲线基本一致.3个有限元模型均能较好地模拟出3块组合试验板的受力全过程.

(a) 试件OCSN1

(b) 试件OCSC1

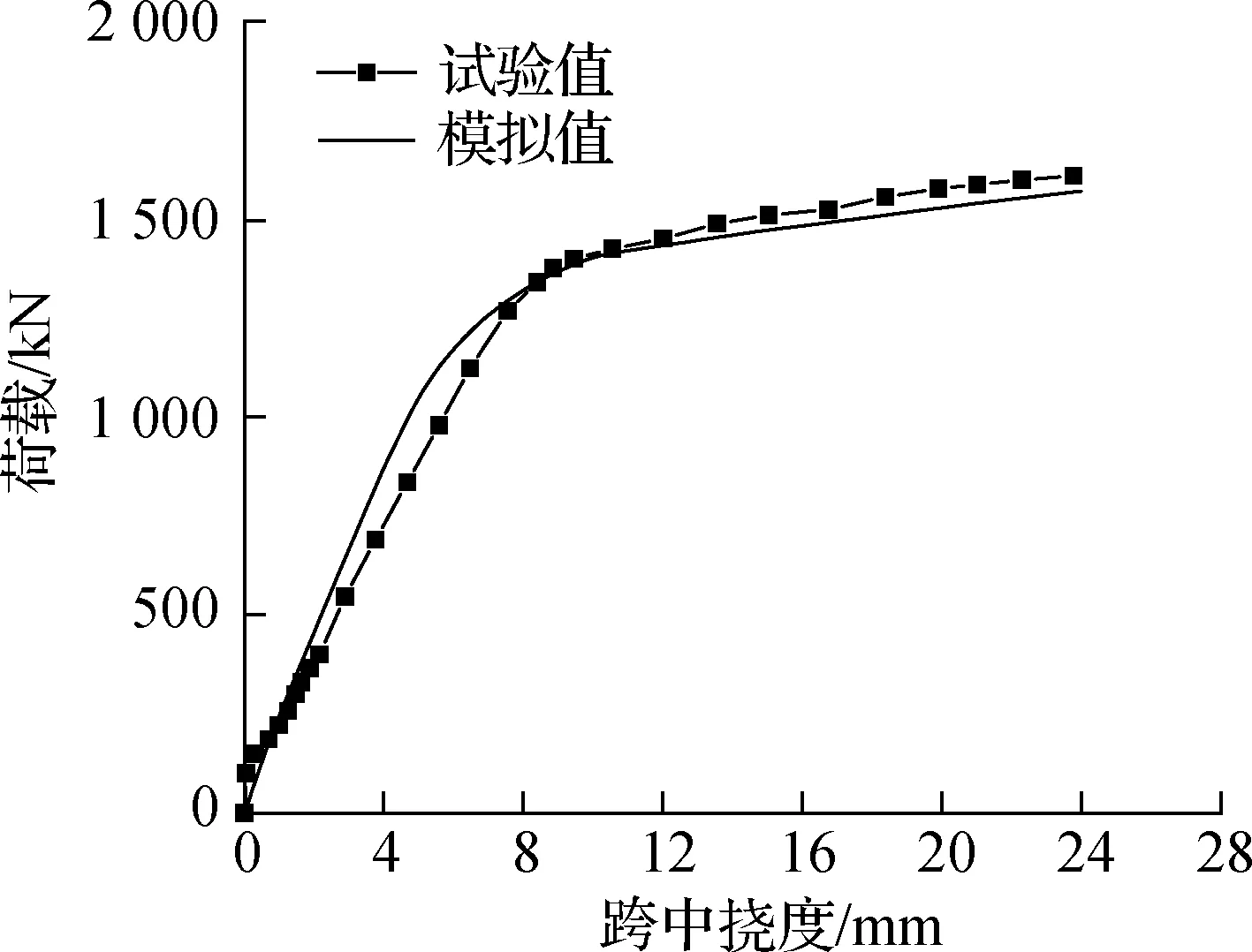
(c) 试件OCSC2

3.4.2 U肋底板荷载-应变曲线对比

有限元模拟得到的跨中荷载-应变曲线与试验结果对比见图13.由图可知,对于组合简支板,有限元模拟曲线与试验曲线基本一致.对于组合连续板,模拟曲线与试验曲线发展趋势类似,存在差距的可能原因在于:试验使用的应变片尺寸相较于模拟网格尺寸更小,导致应变模拟值不够精确.由此可知,有限元模型基本能够反映试验的U肋底板应变变化规律.

(a) 试件OCSN1

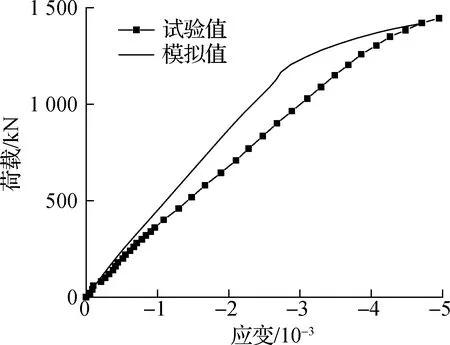
(b) 试件OCSC1

3.4.3 组合板破坏现象对比

图14给出了组合板混凝土层的最大主塑性应变云图.混凝土采用CDP模型模拟,在单元积分点处不会演化出裂缝,但当积分点处最大主塑性应变为正值(即有限元云图中绿色和红色部分)时,该点可视为产生裂缝,以反映混凝土的受拉开裂情况[26].由图可知,混凝土层裂缝分布与试验结果基本一致.试件OCSN1混凝土板在侧面出现竖向裂缝,并沿板顶贯穿.试件OCSC1在跨中位置混凝土板顶部被压碎,底部出现开裂,中间支座位置处的混凝土板顶部也出现开裂.

(a) 试件OCSN1

(b) 试件OCSC1

正交异性钢板的应力云图见图15.由图可知,组合简支板在跨中位置U肋发生屈曲,组合连续板在支座位置U肋发生屈服,与试验现象相符.

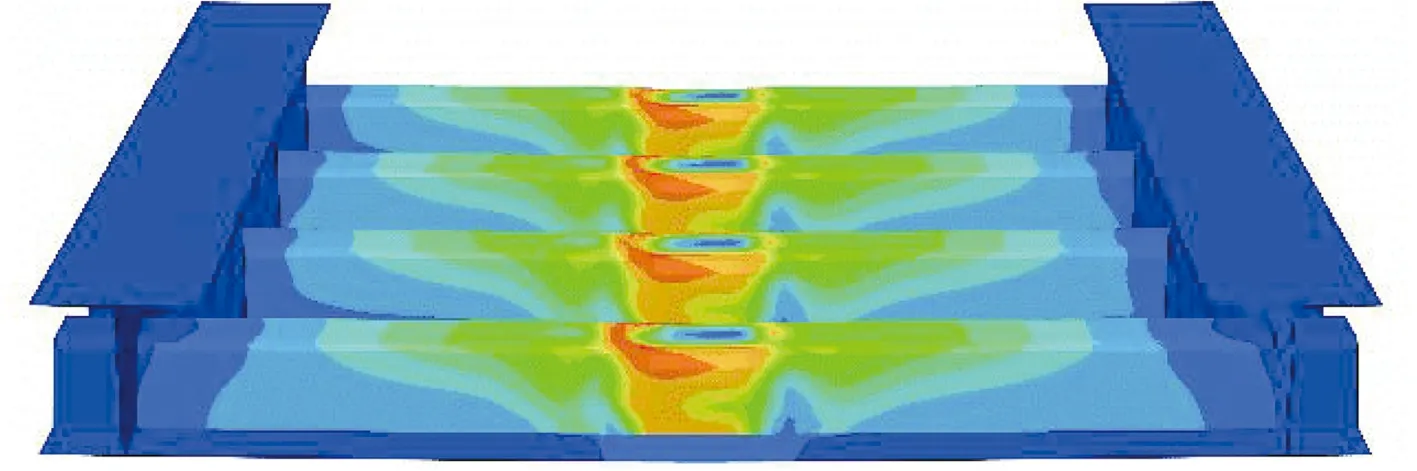
(a) 试件OCSN1

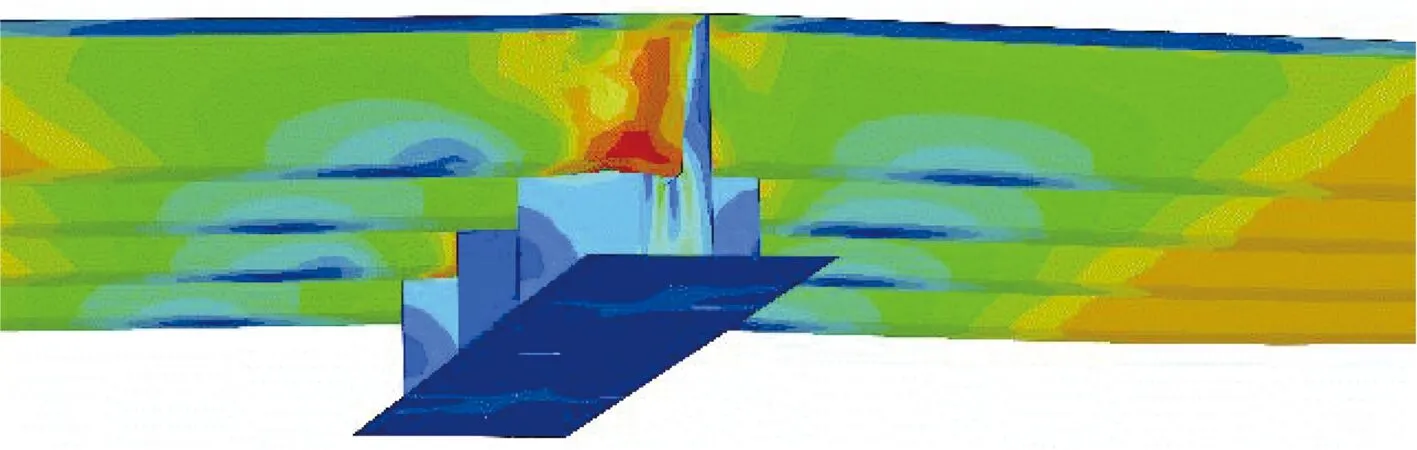
(b) 试件OCSC1

4 组合板影响参数分析

以试件OCSC1为例,利用ABAQUS有限元软件计算负弯矩区截面的弯矩与曲率,探究钢纤维体积分数、钢材强度和混凝土板厚对组合连续板负弯矩区开裂弯矩和极限弯矩的影响.

4.1 钢纤维体积分数的影响

依据《钢纤维混凝土结构设计标准》[27],对不同钢纤维体积分数的混凝土抗压强度和抗拉强度进行取值,结果见表8.按照文献[23]提出的纤维混凝土拟合公式计算得到本构关系,通过在有限元软件中改变钢纤维混凝土的材料属性来模拟不同的钢纤维体积分数.

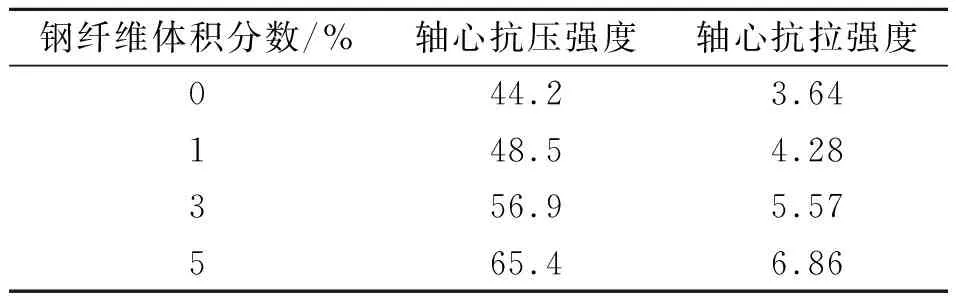
表8 不同钢纤维体积分数的混凝土材料强度 MPa

不同钢纤维体积分数下试件OCSC1的负弯矩区截面弯矩-曲率曲线见图16.由图可知,使用普通混凝土时,试件OCSC1的极限弯矩为390.7 kN·m,开裂弯矩为59.1 kN·m;当混凝土中钢纤维体积分数为1%时,试件OCSC1的极限弯矩为401.2 kN·m,开裂弯矩为76.1 kN·m;当混凝土中钢纤维体积分数为3%时,试件OCSC1的极限弯矩为406.5 kN·m,开裂弯矩为96.1 kN·m;当混凝土中钢纤维体积分数为5%时,试件OCSC1的极限弯矩为411.1 kN·m,开裂弯矩为117.3 kN·m.由此可知,钢纤维能通过增加混凝土的抗拉强度来提高负弯矩区的开裂弯矩.当钢纤维体积分数为1%时,开裂弯矩的提升率最大.但钢纤维体积分数的改变对组合板极限弯矩的影响较小.同时,使用过量钢纤维会导致加工困难[28],从节约材料和方便施工的角度出发,使用适当钢纤维即可.

图16 不同钢纤维体积分数下试件OCSC1的负弯矩区截面弯矩-曲率曲线

4.2 钢材强度的影响

图17给出了不同钢材强度下试件OCSC1负弯矩区截面弯矩-曲率曲线.由图可知,当钢材型号为Q235时,试件OCSC1的极限弯矩为273.3 kN·m;当钢材型号为Q345时,试件OCSC1的极限弯矩为350.6 kN·m;当钢材型号为Q390时,试件OCSC1的极限弯矩为381.1 kN·m;当钢材型号为Q420时,试件OCSC1的极限弯矩为400.9 kN·m.由此可知,增加钢材强度能提高负弯矩区的极限弯矩,但对负弯矩区的开裂弯矩无影响.

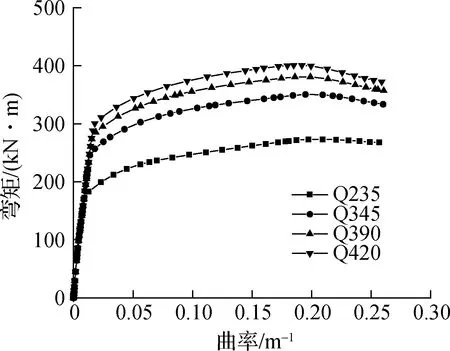
图17 不同钢材强度下试件OCSC1负弯矩区截面弯矩-曲率曲线

4.3 混凝土板厚的影响

图18给出了不同混凝土板厚下试件OCSC1负弯矩区截面弯矩-曲率曲线.由图可知,当混凝土板厚为80 mm时,试件OCSC1的极限弯矩为401.2 kN·m,开裂弯矩为76.1 kN·m;当混凝土板厚为100 mm时,试件OCSC1的极限弯矩为416.7 kN·m,开裂弯矩为84.6 kN·m;当混凝土板厚为120 mm时,试件OCSC1的极限弯矩为435.7 kN·m,开裂弯矩为106.4 kN·m;当混凝土板厚为140 mm时,试件OCSC1的极限弯矩为455.8 kN·m,开裂弯矩为123.1 kN·m.由此可知,增加混凝土板厚能够同时提高负弯矩区的开裂弯矩和极限弯矩.当混凝土板厚为120 mm(即混凝土板厚度和正交异性钢板高度比值为0.8)时,开裂弯矩的提升率最大.

图18 不同混凝土板厚下试件OCSC1负弯矩区截面弯矩-曲率曲线

5 结论

1) 在单点反向加载和两点对称加载下,正交异性钢-混凝土组合简支板和正交异性钢-混凝土组合连续板均呈现典型的弯曲破坏特征,即负弯矩区混凝土板开裂退出工作,正交异性钢板U肋发生局部屈曲,正弯矩区混凝土板被压碎等.正交异性钢-混凝土组合板的荷载-挠度曲线可近似分为弹性、弹塑性和塑性3个阶段,其中弹塑性阶段又分为混凝土开裂段和钢材屈服段.

2) 根据试验结果可知,在混凝土中加入钢纤维可以提高混凝土的抗拉强度,从而增加钢纤维混凝土的开裂荷载.在静载作用下,正交异性钢-混凝土组合连续板钢混界面间的滑移较正交异性钢-混凝土组合简支板小.通过对比组合简支板和组合连续板的荷载-挠度曲线可知,曲线下降段组合连续板的斜率较组合简支板大,这是因为加载到极限荷载时,简支板跨中出现塑形铰,成为可变体系,而连续板仅在支座位置出现塑形铰,结构仍能保持一定的承载能力和变形刚度.

3) 有限元计算结果与实测结果较为吻合,可预测组合板的抗弯性能.当钢纤维体积分数为1%时,钢-混凝土组合板开裂弯矩的提升率最大,但钢纤维体积分数的改变对整体抗弯极限承载力的影响较小.正交异性钢-混凝土组合板的开裂弯矩与正交异性钢板强度无关,极限弯矩则随钢板强度的增加而增大.增加混凝土板厚能够提高组合板的开裂弯矩和极限弯矩,当混凝土板厚度与正交异性钢板高度比值为0.8时,开裂弯矩的提升率最大.