基于DSMC方法的超低轨道卫星阻力特性分析
杭晓晨 李彦斌 孔祥宏 陈 强 费庆国
(1南京林业大学机电工程学院, 南京 210037)
(2东南大学空天机械动力学研究所, 南京 210096)
(3上海卫星工程研究所, 上海 201109)
超低轨道卫星运行于180~300 km高度地球轨道.相比于传统低轨道,超低轨道卫星侦查地面的光学成像分辨率成倍提高,雷达功耗降低,使得卫星小型化成为可能,从而大大降低了卫星的研制成本.超低轨道卫星在空间信息对抗方面具有优势,美国、欧洲、日本等国家相继对此类卫星投入了大量研究[1-3].卫星在超低轨道上处于稀薄气体大气环境,气动阻力不可忽略,经常需要离子发动机进行速度补偿,以保证卫星的轨道机动和姿态控制.因此,研究超低轨道卫星气动阻力特性和精确预测方法,对该类卫星的合理结构设计具有重要意义.
180~300 km轨道高度属于稀薄气体环境,气体分子间距大,克努森数高,不满足传统航空领域的气体连续性假设,基于纳维-斯托克斯方程的连续流体分析方法不再适用.目前,预测计算卫星阻力的方法主要有工程近似算法和数值仿真方法.Titov等[4]提出了低轨道卫星阻力计算的近似表达式,认为阻力与大气密度、迎风面投影面积以及来流速度平方呈正比关系.该表达式能够在卫星结构设计初期阶段提供快速的阻力近似预测.数值仿真方法包括面元积分法[5]、格子玻尔兹曼法[6]、直接模拟蒙特卡洛(direct simulation Monte Carlo, DSMC)方法[7]、试验粒子蒙特卡洛法[8]等.其中,DSMC方法是一种基于分子动力学的改进数值算法,利用概率统计判断分子间是否发生碰撞,相比于传统分子动力学仿真可以极大降低计算资源消耗.
Moe等[9]采用DSMC方法研究了稀薄气体环境分子-壁面碰撞模型,认为能量调节系数兼顾了不同的气动作用,并估算了阻力系数的不确定性.Mehta等[10]利用DSMC方法仿真分析了漫反射模型和准镜面模型对卫星阻力特性的影响,发现2种壁面碰撞模型在GRACE卫星上的阻力差异约为15%.DSMC方法也被用于分析航天器再入大气层时的稀薄大气环境,如文献[11]研究了航天器再入阶段的气动特性和动力学稳定性,文献[12]研究了气动加热效应等.李志辉等[13]将DSMC方法应用于模拟阿波罗指令舱稀薄气体动力学特征中.周伟勇等[14]采用部分计算总体叠加的思路,分析了复杂外形卫星的气动力,给出了卫星减阻的设计建议.黄飞等[15]基于DSMC方法分析了GOCE卫星的气动特性,讨论了不同物面反射系数对阻力特性的影响.靳旭红等[16-18]采用试验粒子蒙特卡洛方法,分析了大气模型、飞行高度、轨道纬度等对超低轨道卫星阻力特性的影响规律.
本文采用DSMC方法对一典型超低轨道卫星进行了三维分子动力学仿真,预测了卫星阻力特性,研究了卫星不同几何参数对气动特性的影响规律.
1 DSMC方法
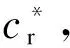
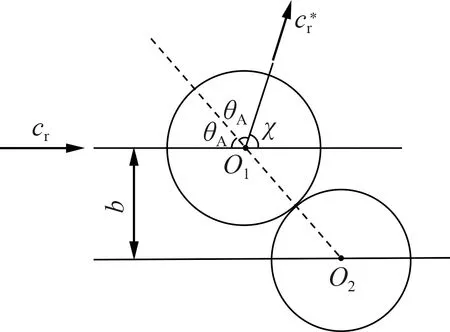
图1 VHS二元碰撞模型示意图
(1)
σT=πd2
(2)
式中,碰撞参数b为质心参考系中未扰动轨迹的最近距离,可由b=1/2(d1+d2)sinθA计算得到,其中θA为相对速度与球心连线的夹角;d为可变硬球分子的直径参数,是气体分子碰撞对中相对速度cr的逆幂律形式函数.
稀薄流气体分子与物面的相互作用直接影响DSMC方法对阻力特性的计算精度.针对卫星结构中与来流平行或小夹角的壁面,采用镜面反射模型,即假设气体分子与物面产生弹性碰撞.针对卫星结构中与来流垂直或大夹角的壁面,采用漫反射模型,即假设气体分子与物面发生非弹性碰撞,且反射后的气体分子向各个方向散射,散射时的分子速度满足平衡的Maxwell分布.采用动量协调系数来描述反射分子的动量特性改变,法向动量协调系数σn表示分子与物面碰撞过程的法向动量改变,切向动量协调系数στ表示切向动量改变,计算公式分别为
(3)
(4)
式中,pi、τi分别为入射分子的法向压力和切向压力;pr、τr分别为反射分子的法向压力和切向压力;pw为壁面法向压力.发生镜面碰撞时,σn=στ=0;发生漫反射碰撞时,σn=στ=1.
DSMC方法将抽样的气体分子以概率计数的方式来表示真实环境中大量的真实分子,从而降低计算量.本文采用非时间计数法(no time counter,NTC)[7],在一个DSMC网格内,选取潜在可能碰撞对,当其碰撞概率P大于生成的随机数R(0 以一典型超低轨道卫星为研究对象,轨道高度为268 km,环境大气密度为55.09 ng/m3,环境温度为951.5 K,飞行速度为7 740 m/s.基于DSMC方法研究卫星的阻力特性,分析结构构型对阻力特性的影响. 卫星几何模型如图2所示.卫星本体柱段需容纳一定体积的载荷,两侧太阳翼总面积约为10.2 m2.以柱体为长方体、横截面为矩形、柱体长3 m为基准模型,基于DSMC方法分析卫星在轨阻力特性,并研究网格密度、头锥形状、长细比等参数对阻力特性的影响规律. 图2 典型超低轨道卫星几何模型(单位:mm) 采用DSMC方法仿真稀薄气体时,卫星结构的网格过疏可能会导致对物面的曲面模拟失真,计算结果精度较低;过密的网格则会因为模拟大量分子壁面碰撞而加大计算资源消耗.以卫星的圆形平板头锥和半球形头锥为例,在200 km轨道大气环境下,研究网格密度对DSMC方法计算气动阻力结果的影响. 图3给出了不同网格密度设计方案.圆形平板直径为1 m,厚度为10 mm,低、中、高密度网格分别包含524、960、1 960个三角形网格,对应的网格特征长度分别为100、50、30 mm,相对尺度分别为10%、5%、3%.半球形头锥底面外接圆直径为1 m,低、中、高密度网格分别包含500、1 000、2 000个三角形网格,对应的网格特征长度分别为110、75、55 mm.不同网格密度模型受到的气动阻力见表1. (a) 低密度 (b) 中密度 (c) 高密度 表1 不同网格密度模型受到的气动阻力 图4给出了半球形头锥的DSMC分析结果.由图可知,迎风面中心处压强最大,越靠外缘则压强越小.半球附近存在高压区,这是因为气体分子在头锥表面撞击后获得反向动量,导致区域内气体分子密度增加.由表1可知,低密度网格与中密度网格的气动阻力差在0.3 mN以内,中密度网格与高密度网格的计算结果几乎无差别,故后续数值分析均采用中等以上的网格密度方案,即在对卫星表面划分网格时,采取网格相对尺度在3%~5%范围内值取. (a) 表面压强场 (b) 全域压强场 本节研究不同的卫星头锥形状对受到气动阻力的影响.考虑锥度为60°、90°、120°的四棱锥、六棱锥、八棱锥、圆锥以及半球形头锥和圆形平板头锥总共14个分析模型(见图5).实际工程中结构设计必须考虑星体的载荷尺寸约束,将所有头锥模型的尺寸均设为底面投影外接直径为1 m的圆. (a) 锥角60° (b) 锥角90° (c) 锥角120° 不同的头锥模型在平飞(θ=0°)、竖飞(θ=90°)两种飞行姿态下的气动阻力计算结果见表2.由表可知,圆形平板头锥、半球形头锥、圆锥在平飞姿态下具有完全相同的迎风面投影面积0.785 m2,所受气动阻力相差不大,均为18.50~18.95 mN,故迎风面投影面积是影响气动阻力的主要因素.四棱锥、六棱锥、八棱锥等其他模型底面投影外接圆,故迎风面积均小于0.785 m2,受到的阻力幅值也较小.图6给出了头锥模型的迎风面与阻力散点图.由图可知,头锥受到的阻力与迎风面积具有线性相关性. 图6 不同头锥模型的阻力特性 同时表2给出了不同头锥模型平飞姿态时的阻力系数CD,圆形平板头锥的阻力系数最大为2.13,60°圆锥阻力系数最小为2.08.在相同的迎风面投影面积情况下,平飞姿态下头锥的锥角越小,头锥越尖,受到阻力越小,但锥角不同导致的平飞阻力差异在1 mN范围内.在竖飞姿态下,锥角越小,迎风面越大,因此竖飞时阻力水平越高.例如,60°锥角的圆锥平飞阻力为18.49 mN,为同一迎风面积下的最低阻力值,但其竖飞时阻力为10.77 mN,阻力值较大.究其原因在于,在气体粒子与物面的碰撞中,头锥越尖,壁面与来流的夹角越小;气体粒子撞击壁面的过程中,法向动量改变越小,切向动量改变越大,即压差阻力占比较小,摩擦阻力占比较大. 表2 不同头锥阻力特性结果 为进一步揭示压差阻力和摩擦阻力的关系,研究了不同高度梯形圆锥模型的气动阻力变化(见图7),与基准的60°锥角圆锥模型进行对比,结果见表3.显然,梯形圆锥高度越低,平飞姿态下头锥将受到越多来流方向气体分子的撞击,摩擦分量占比越小,总阻力略微升高. 图7 梯形圆锥高度影响分析模型 表3 梯形圆锥阻力特性 mN 卫星星体长细比也是初期结构设计时必须要考虑的重要因素.本节研究了不同结构星体的阻力特性随长细比的变化规律.考虑载荷需要,卫星模型星体横截面均设计为外接直径为1 m的圆,星体形状分别为四棱柱、六棱柱、八棱柱与基准圆柱,利用DSMC方法分析得到阻力特性,结果见表4.同时也给出了圆柱星体带圆锥头锥结构所受的气动阻力值,对比分析了同投影面积下头锥对气动阻力特性的影响. 表4 不同长细比星体结构阻力特性 mN 由表4可知,对于同样的星体横截面,在迎风面投影面积相同的情况下,长细比越大,星体所受阻力也越大.究其原因在于,DSMC仿真中,大量的气体分子与星体侧面发生小入射角的摩擦型碰撞,星体长细比越大,气体分子与星体侧面接触面积越大,引起的摩擦阻力分量也越大.针对本文采用的卫星模型,长细比每增加1,阻力增加约5%~8%. 利用欧洲GOCE卫星算例,验证本文提出的DSMC方法.GOCE卫星是世界上第1颗重力梯度测量卫星,主体由卫星本体、太阳翼和稳定翼构成.星体为八棱柱,太阳翼面积较大,稳定翼面积较小,其分析模型如图8所示. 分析域为20 m×10 m×10 m的立方体.根据网格收敛性结论,将GOCE卫星表面划分为6 980个网格,网格相对尺度为3%.分析结果如图9所示,GOCE卫星的六边形头部压强最大,太阳翼、尾翼与来流接触面呈现较大压强.由全场压强云图可以看出,气体分子密度在卫星头部附近最高;相对于远处流场,气体分子在尾翼附近、星体侧面更为聚集.该卫星在268 km轨道大气环境下,平飞时所受气动阻力为8.8 mN.将本文方法获得的GOCE卫星在典型轨道200~268 km的气动阻力结果与文献[17]中GOCE卫星在不同大气模型下的阻力曲线进行对比,对比结果见图10.由图可知,本文方法结果与文献[17]中采用多种大气模型的计算结果吻合良好. (a) 表面压强场 (b) 全域压强场 图10 GOCE卫星阻力特性与文献值对比 针对典型超低轨道卫星结构(见图2和图11),研究整机在不同姿态和攻角飞行时所受的阻力,并分析平飞姿态下全动尾翼转动对整体气动特性的影响.全动的水平尾翼为梯形,安装于星体尾部高于整星中轴线40 mm处,面积为0.2 m2.分析结果见表5. 图11 卫星尾翼位置(单位:mm) 由表5可知,与200 km轨道的头锥、星体算例结果相比,GOCE卫星每单位投影面积所受到的空气阻力明显减小.究其原因在于,268 km轨道的空气更为稀薄,每立方米空气分子数为1.144×1015,远小于200 km轨道中每立方米空气分子数(5.8×1015),相应的气体分子碰撞次数和碰撞概率均降低,因此阻力较小. 表5 卫星整机与尾翼多攻角阻力特性 全动尾翼偏转角会加大迎风面积,攻角为10°时附加阻力为0.09 mN,升力为0.031 mN,升阻比为0.34;攻角为20°时,附加阻力为0.35 mN,升力为0.041 mN,升阻比为0.12;攻角为30°时,附加阻力为0.56 mN,升力为0.053 mN,升阻比为 0.10.因此,在稀薄气体自由分子流情况下,升阻比随攻角增加呈下降趋势;而在连续流环境下,随攻角增加,升阻比先增大后减小.由此可见,在升力特性方面,超低轨道的稀薄气体环境与连续流环境具有较大差异.尾翼偏转角由0°增加到30°时,升力逐渐增大,升阻比在0.10~0.34范围内先增大后减小. 1) 基于DSMC方法分析了典型超低轨道卫星的阻力特性,采用小攻角镜面反射、大攻角Maxwell漫反射联合模型,研究了卫星结构几何构型对阻力特性的影响规律.结果表明,迎风面投影面积是影响卫星阻力的主要因素.在相同的迎风面投影面积下,较尖的头锥结构能略微降低平飞阻力. 2) 星体长细比对卫星阻力有较大影响.相同的投影面积情况下,星体越长,卫星侧面与气体分子的接触面积越大,产生切向的摩擦阻力越大.对于本研究中的卫星,长细比每增加1,阻力增加约5%~8%. 3) 设计的卫星结构在268 km典型超低轨道下,尾翼偏转角由0°增加到30°时,升力逐渐增大,升阻比在0.10~0.34范围内先增大后减小. 4) 对于GOCE卫星,本文分析得到的阻力特性结果与文献[17]中多种大气模型结果吻合良好,验证了DSMC方法在计算超低轨道卫星阻力特性时的准确性.2 低轨卫星阻力特性

2.1 网格密度对DSMC结果收敛性的影响


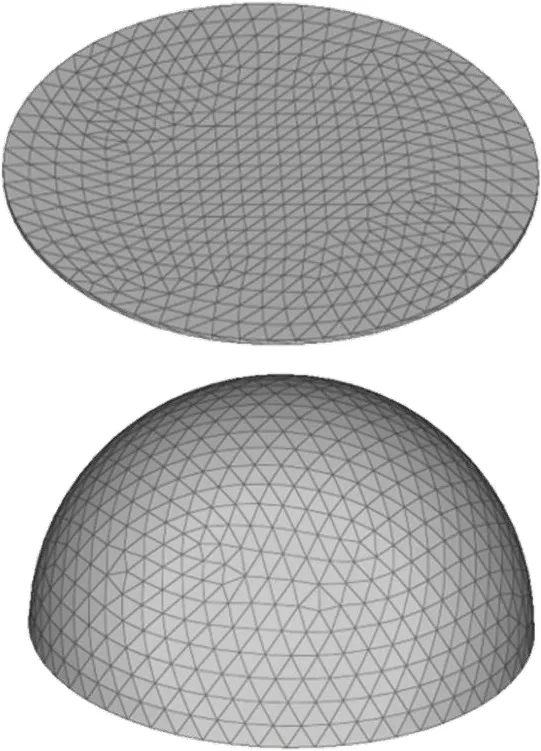


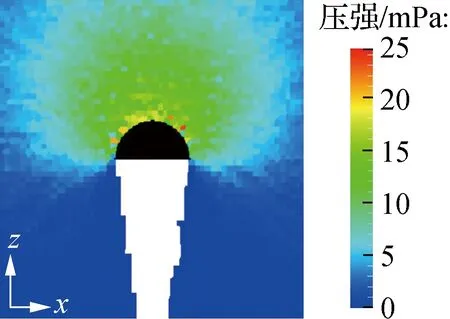
2.2 头锥几何参数对阻力特性的影响

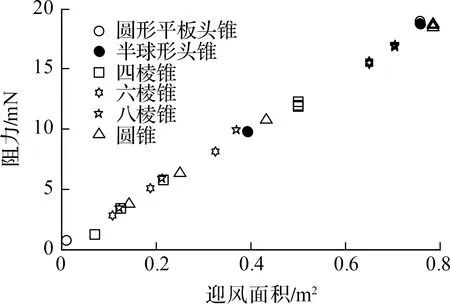
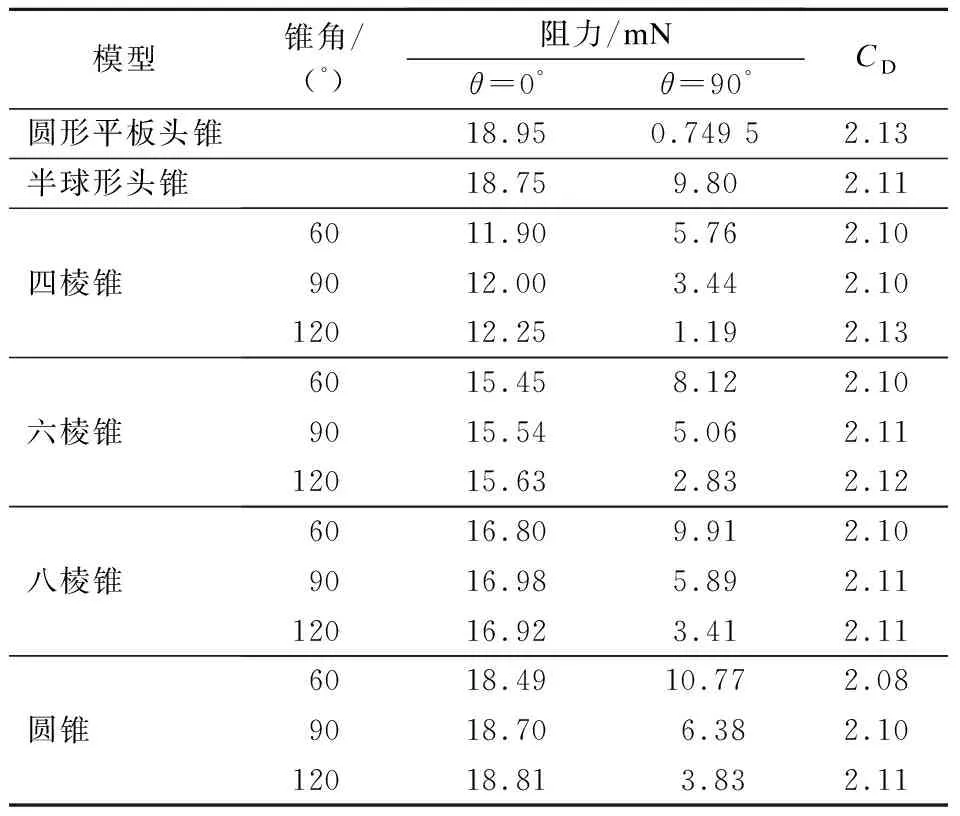
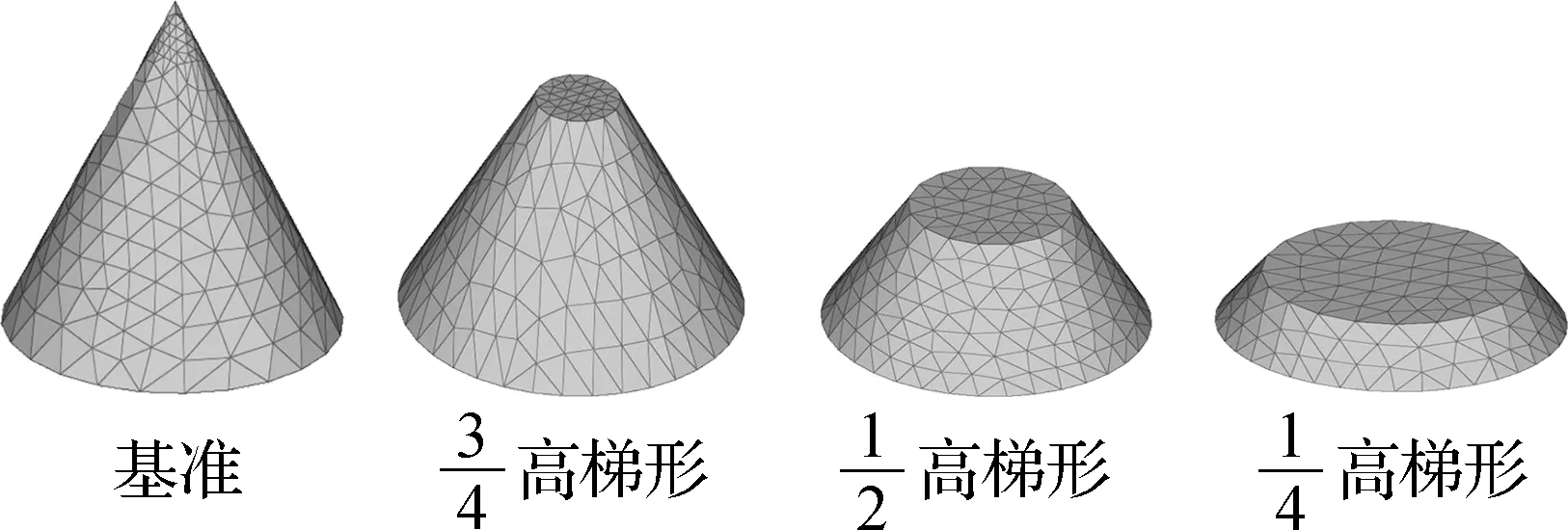

2.3 卫星星体长细比对阻力特性的影响

2.4 基于DSMC方法的整星气动特性分析
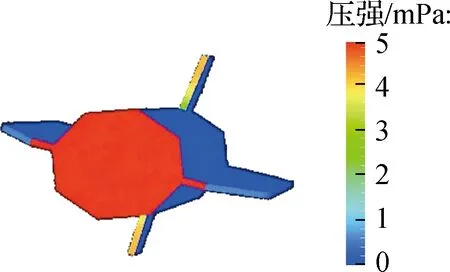



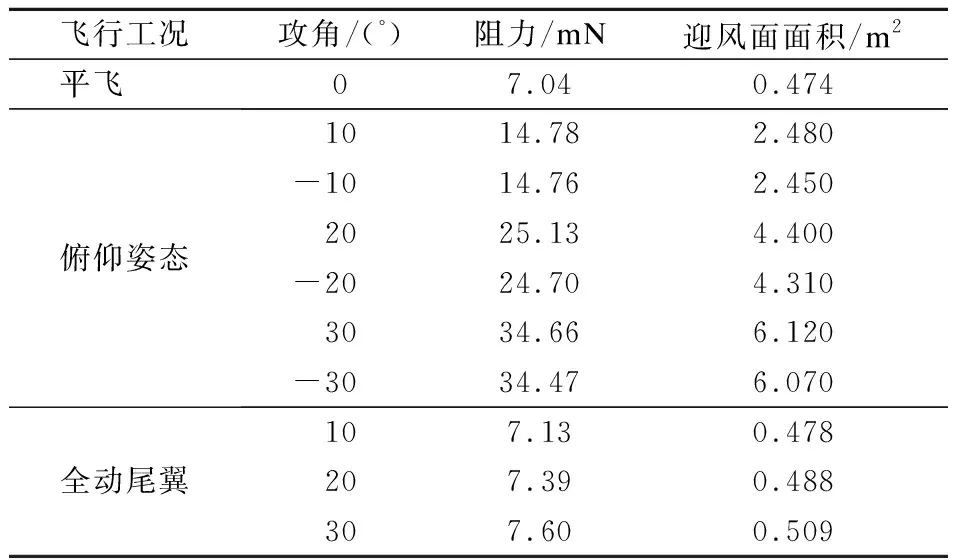
3 结论

