新型张拉整体管道机器人运动性能

陆金钰 许植胤 刘继磊

(东南大学土木工程学院, 南京 211189)

随着新型城市建设速度的加快,管道在日常生活以及工业制造中的应用逐渐增大,对其探测、检修的需求也越来越多[1].但是采用人工清理维修管道需要拆卸管道,费时费力,很多管道也隐藏在人工难以抵达的建筑物内部或是深埋于地下.因此国内外很多学者开始研究利用机器人对管道进行探测[2-3],以及时发现管道破损之处.机器人可以代替人工进入狭小的空间作业,在很多危险的管道环境下机器人的优势更加明显[4].

张拉整体结构是由受压杆件和受拉绳索组成的索杆张拉结构[5].当将其应用于机器人中时,张拉整体结构能够承受一定的冲击而不受损坏,具有质量小、可折展、便于储存运输、占用空间小等特点[6].目前已有多种构型、多种运动步态的机器人得到深入研究,如滚动式球形机器人[7]、膜驱动机器人[8]、蠕动式三杆机器人[9]、脊柱型机器人[10]等.随着张拉整体机器人的不断发展,也有学者将其应用到管道探测当中[4,11-12].但是设计出的机器人由多个四面体框架通过索连接而成,四面体框架本身无法变形,构型较为复杂笨重,且运动时需要索杆混合驱动,控制构件多,控制策略繁琐.

张拉整体管道机器人横截面积小,在管道中工作时不易造成管道堵塞,相较于其他管道机器人适用性更强,同时具有轻质、可折展等优点.基于此,本文首先以三杆星型张拉整体作为基本单元,设计了一种基于纵波法运动步态的新型张拉整体管道机器人.该管道机器人由多个相同单元构成,具有模块化装配、驱动简单和方便控制等优点.然后采用ADAMS动力学仿真软件,建立了五单元机器人仿真模型,并验证了该设计的可行性.最后,基于前进距离、能量消耗和稳定性参数3个评价指标,研究了不同模型参数和不同工作条件下机器人的运动性能.

1 新型张拉整体管道机器人

1.1 三杆星形张拉整体单元拓扑模型

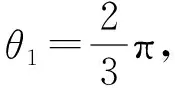
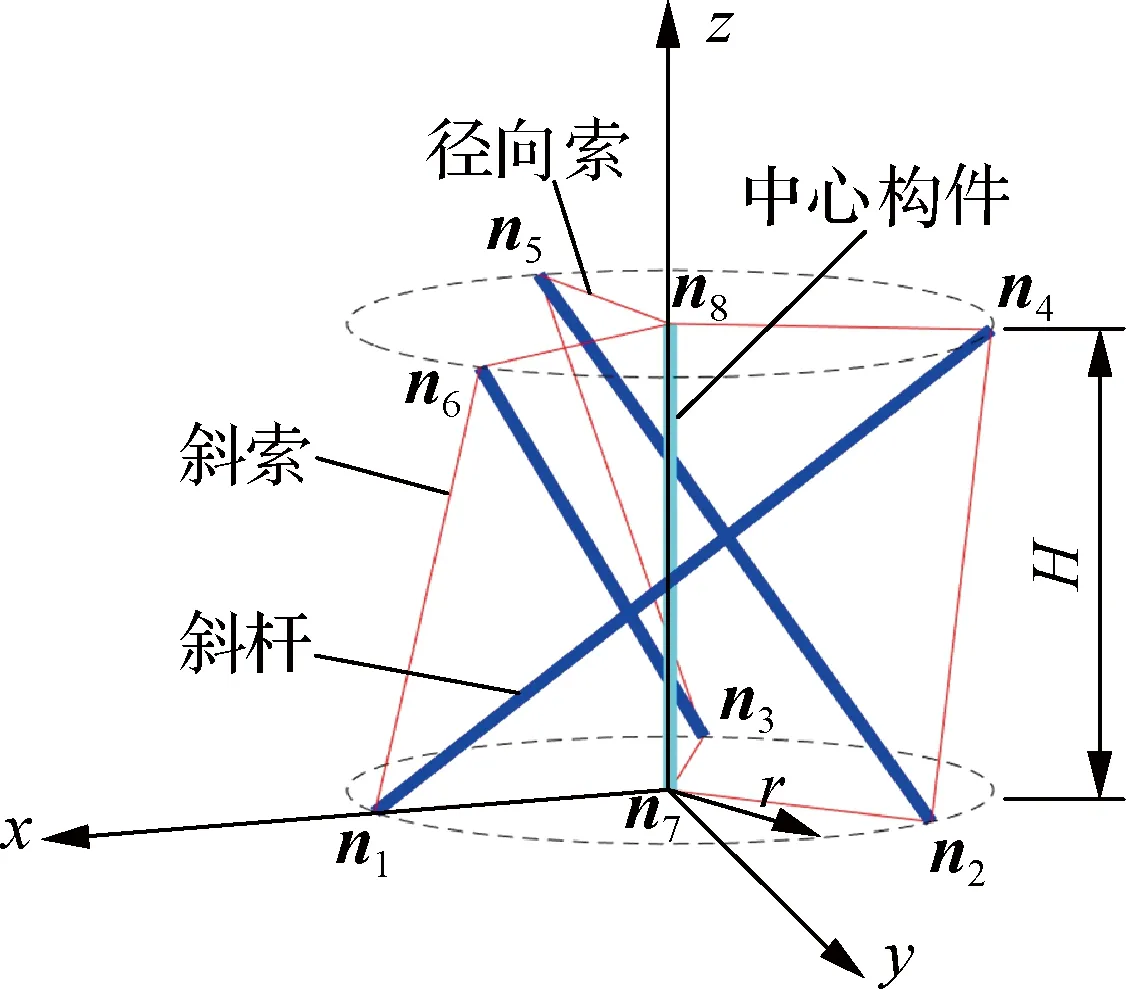
图1 三杆星形张拉整体的拓扑模型

限定下底面圆位于xy平面,中心构件位于z轴,n1点位于x轴,则三杆星形张拉整体结构的节点坐标计算公式如下:

n1={r,0,0}T,n2=R1n1,n3=R1R1n1
n4=R2{r,0,H}T,n5=R1n4,n6=R1R1n4
n7={0,0,0}T,n8={0,0,H}T

(1)

通过坐标和连接拓扑关系,可以根据文献[14]中的平衡矩阵理论对结构单元进行分析.计算得三杆星形张拉整体结构的自应力模态数s=1,机构位移模态数m=6,且判定其为几何稳定结构[15].

1.2 驱动策略可行性判定

根据文献[16],三杆星形张拉整体结构具有一定的折展性能,改变中心构件的长度可以调整结构形态,如图2所示.图中,h为中心构件长度,R为结构端面半径.

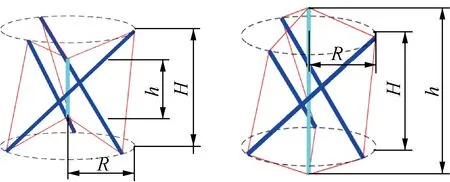
图2 h≠H时的三杆星形张拉整体结构

在折展过程中,中心构件长度变化会导致形态发生变化,其他结构参数也随之受到影响.此时,需要对结构进行形态分析,确定形态变化后的结构参数.本文采用动力松弛法解决上述问题.节点的初始坐标根据式(1)计算,中心构件长度h=H,质点系此时保持平衡.当中心构件长度变为h+e后(e为中心构件的驱动长度),节点n7、n8的坐标为n7={0,0,-e/2}T和n8={0,0,H+e/2}T.为保持中心杆长不变,固定节点n7、n8,其余节点在不平衡力下振动.关于动力松弛法的计算公式参见文献[17].

以H=200 mm、r=100 mm、e=150 mm的三杆星形张拉整体为例,判定驱动策略是否可行.

在经过动力松弛法迭代后,三杆星形张拉整体结构在变形前后的形态参数如表1所示.经过计算,相较于变形前,结构发生了径向收缩,如图3(a)所示,结构的端面半径R由100 mm降到85.41 mm.而节点不平衡力经过416次迭代,下降到了设置的限值1 mN,如图3(b)所示.变形前后,斜索的长度变化最大,由206.59 mm增大至228.43 mm,增加了10.6%;径向索长度变化较小,增大了5.63 mm,约为5.63%;斜杆由于设置的轴向刚度远大于索,其长度变化几乎可以忽略.在驱动星型张拉整体单元伸长时,所有构件的预应力均增大,表明若结构施加了初始预应力,机器人在整个运动过程中均不会因为丧失预应力而丧失刚度.

表1 驱动前后的形态参数

(a) 单元状态叠加

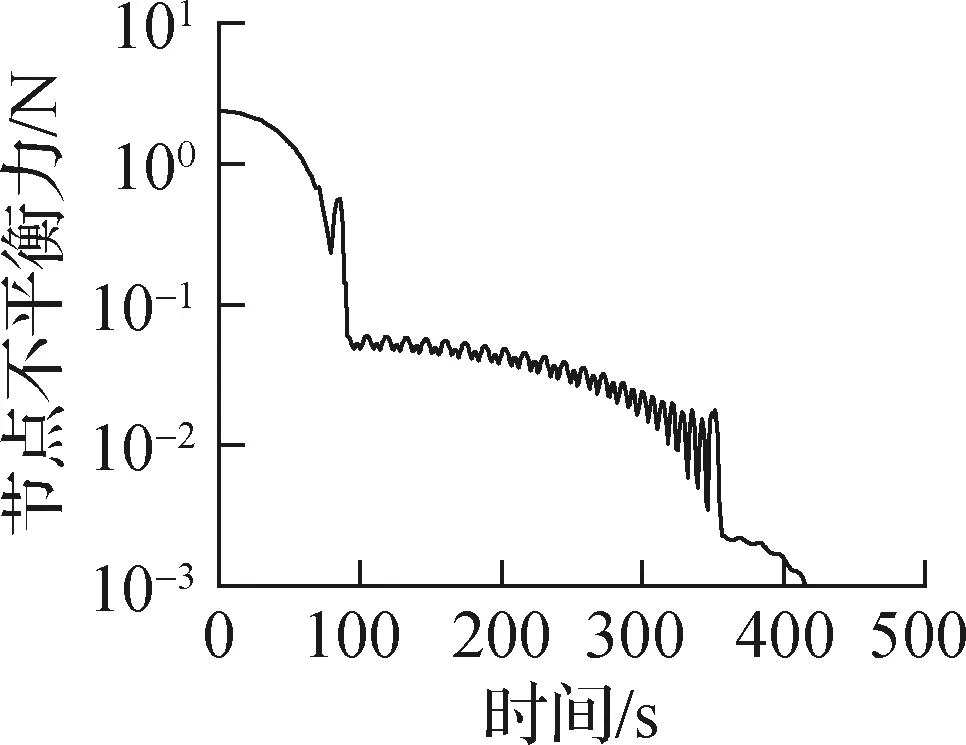
(b) 节点不平衡力收敛曲线图3 动力松弛法计算过程

根据最终平衡构型的各个节点坐标,应用平衡矩阵理论对结构单元进行分析[14],分析结果为:s=1,m=6,且乘积力矩阵Q为正定矩阵,结构几何稳定[15].在变形后,索构件均伸长,表明索在张拉整体变形过程中不会松弛;同时杆构件缩短,承受压力,符合张拉整体索受拉杆受压的特性.

分析结果表明:对于H=200 mm、r=100 mm的三杆星形张拉整体,驱动中心构件由200 mm伸长至350 mm的驱动策略是可行的.

1.3 机器人构型设计

张拉整体管道机器人构型由多个相同的三杆星形张拉整体单元串联组成.相邻单元的连接方式如图4(a)所示.初始平衡状态下,将单元平放使得中心构件与地面平行,且单元中心构件长度h=H.每个张拉整体单元中有2个杆端点接触地面,相邻单元仅通过中心构件连接,连接方式为刚接.所有单元的中心构件保持共线,机器人与地面的接触点分布合理,能够保持平衡.

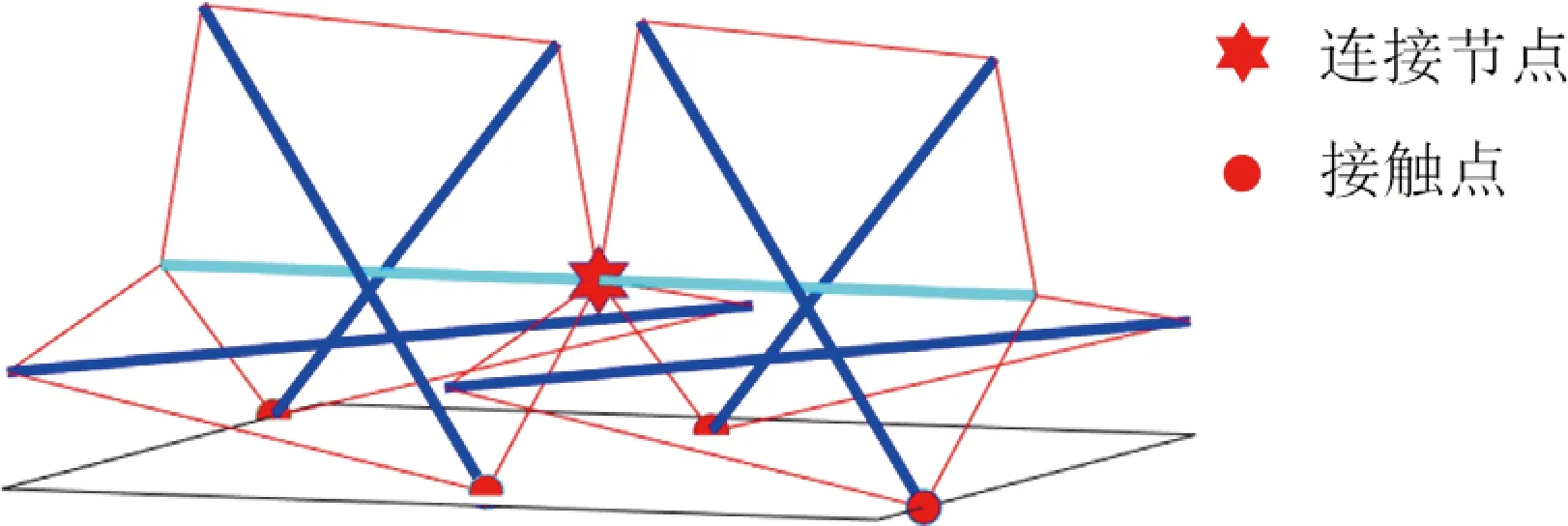
(a) 单元连接方式

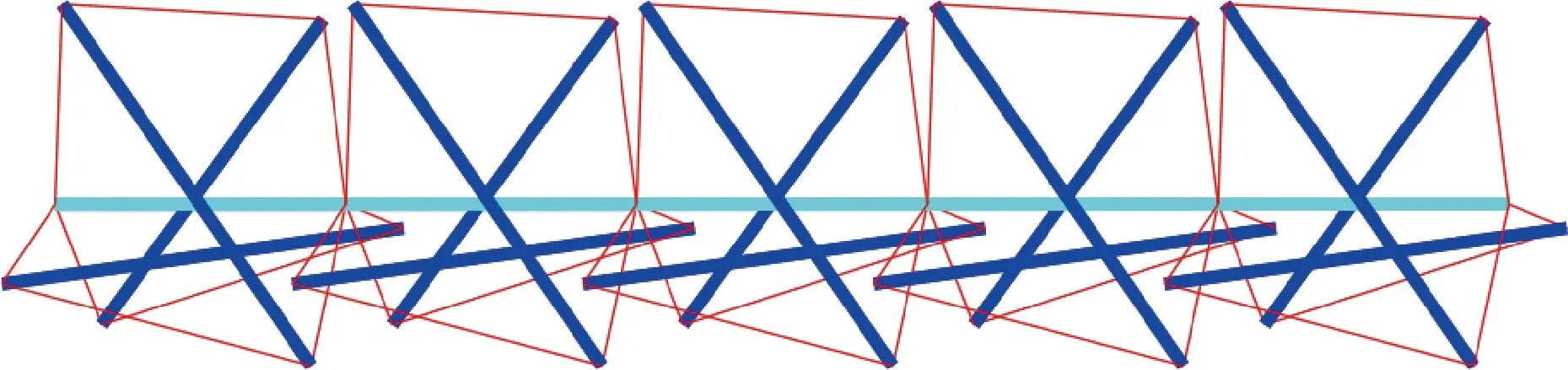
(b) 五单元机器人构型

通过该连接方式,根据单元高度H、底面圆半径r和单元数量n三个参数可以确定张拉整体管道机器人构型.当H=200 mm、r=100 mm、n=5时的机器人构型如图4(b)所示.

1.4 纵波法运动步态

在张拉整体管道机器人构型中,通过控制中心构件伸缩,每个单元的纵向长度均可以发生变化.令所有中心构件伸长缩短的总时间一致,设为T,按照如图5所示的顺序调节各个中心构件的伸缩,可形成机器人运动步态.具体步骤如下:

图5 纵波法运动步态

① 初始时刻,单元1～5的中心构件长度h=H.

② 0～T时,单元1中心构件伸长,长度变为h+e.

③T～2T时,单元1中心构件缩短,恢复至h.同时,单元2中心构件伸长,长度变为h+e.

④ 重复上述过程,直到5T～6T时,单元5缩短,机器人所有单元复位,理论前进距离为中心构件伸长量e.

由于该步态与物理学中纵波的传递方式类似,本文称为纵波法运动步态.对于一个有n个单元的机器人,纵波法步态可以分为开始阶段、运动阶段和结束阶段,分别对应0～T、T～nT和nT～(n+1)T.在开始或结束阶段,仅第1个单元或第n个单元处于伸长状态,径向收缩,与管道壁的接触面积少,而非驱动单元径向不收缩,尺寸大,与管道相接触,提供较大的摩擦力以保持静止状态.在运动阶段,相邻单元一伸一缩,且伸缩速度相同,使得被驱动单元总长度不变,理论上不会引起其他非驱动单元的位置变化.

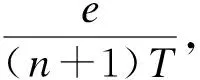
2 仿真模型算例

2.1 ADAMS仿真模型

为了验证纵波法运动步态在张拉整体管道机器人中的可行性,本节以图4(b)中的机器人为例,进行仿真测试.

机器人仿真模型采用ADAMS建立,如图6(a)、(b)所示,模型的主要建模参数如表2所示.其中,杆索构件尺寸的选取参考文献[18],摩擦系数的选取参考干燥条件下铁和橡胶的摩擦系数,该接触条件是机器人实际应用的一种可能情况,即橡胶端点的机器人在铁质管道中前进.机器人的前进方向为y轴正方向,重力方向为z轴负方向.按照纵波法产生的步态机理,采用step函数输入5个单元的驱动控制函数,如图6(c)所示.为了让机器人驱动时从稳定状态开始,单元1在t=4 s时开始伸长.

表2 ADAMS仿真建模参数

(a) 仿真机器人模型轴测图

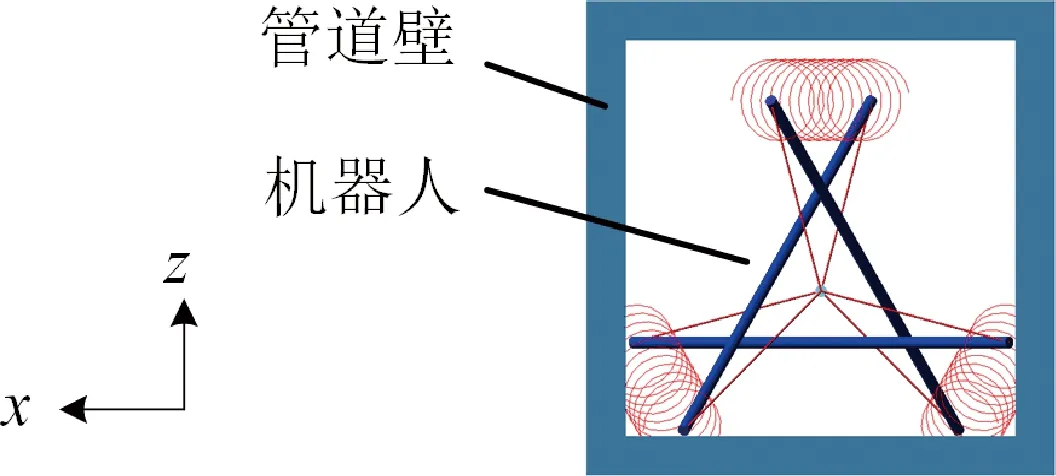
(b) 仿真机器人模型侧视图

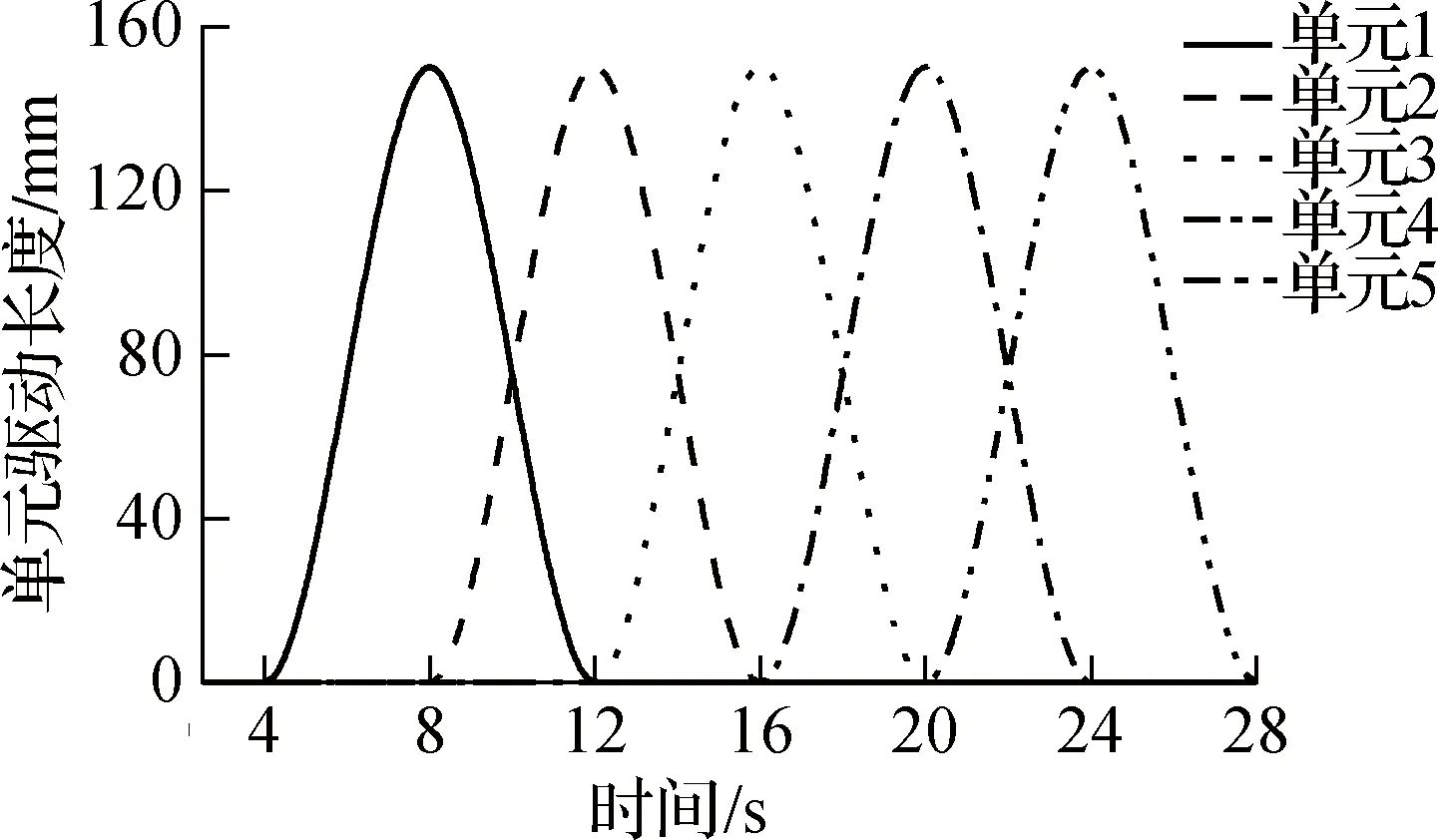
(c) 中心驱动杆驱动控制函数

2.2 机器人运动性能评价指标

本文研究的机器人运动性能包括前进性能、耗能性能和稳定性能,分别采用一次纵波法运动步态下的前进距离Δd、能量消耗ΔW和稳定性参数Δs作为评价指标.3个指标通过驱动过程中的数据定量计算.

前进距离Δd通过驱动前后机器人头部的坐标变化计算,即

(2)

能量消耗ΔW通过每个单元的驱动构件做的功进行计算,即

(3)

式中,ΔW为能量消耗,J;Fi为第i个中心杆的压力,N;vi为第i个中心杆的驱动速度,m/s.

稳定性参数Δs通过行进过程中机器人头尾的最大高度差计算,即

(4)

式中,Δs为稳定性参数,mm;zhead、ztail分别为机器人头、尾的z坐标,即高度,mm.

由图3(a)可知,单元在伸长过程中,径向会伴随着收缩.当单元前后串联时,单元径向的收缩会导致机器人高度的变化,尤其是在按照纵波法这样前后非对称变化的步态运动时,高度变化也会出现前后不对称的现象,这也就导致了机器人头部和尾部的高度差.高度差越大,稳定性参数Δs越大,机器人倾斜现象越严重,运行越不稳定.

2.3 仿真结果

仿真中机器人的形态以及3个运动性能评价指标如图7所示.由图7(a)、(b)可知,在t=4～8 s内,机器人极速前进,向前运动近150 mm,前进距离曲线与图6(c)所示的单元1驱动长度曲线基本一致.机器人在t=8～28 s稍向后移动,也即在后续4个张拉整体单元被驱动时,机器人会向后略微移动.在t=28 s,机器人复位,此时前进距离为133.53 mm,略小于理论前进距离150 mm,但是总体上机器人仍向前移动.从仿真过程中还可以看出,张拉整体单元由于自重会产生z向的压缩和横向的扩张,而机器人左右两侧的管道壁恰好可以约束这一横向扩张,避免张拉整体单元变形过大.同时张拉整体和管道壁的接触也可以增大摩擦力,避免机器人向后滑动.

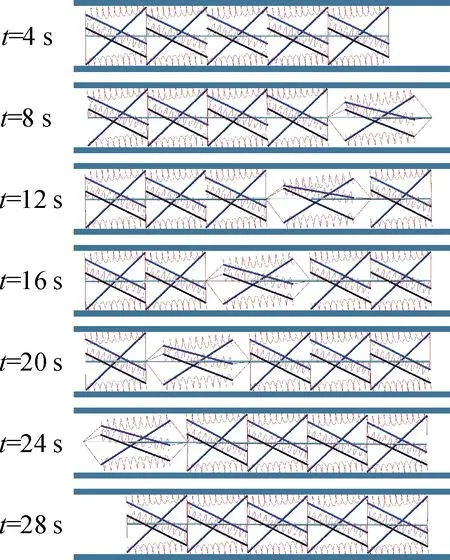
(a) 机器人仿真过程(俯视图)

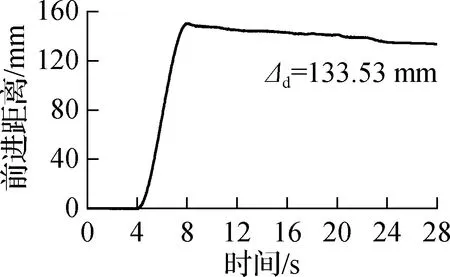
(b) 机器人前进距离变化

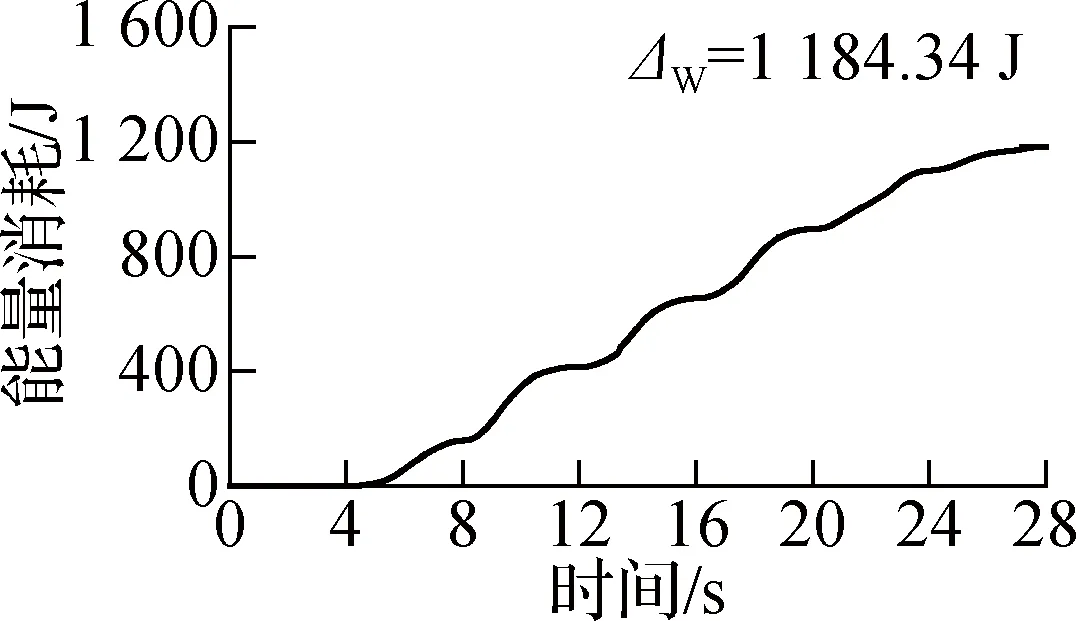
(c) figure

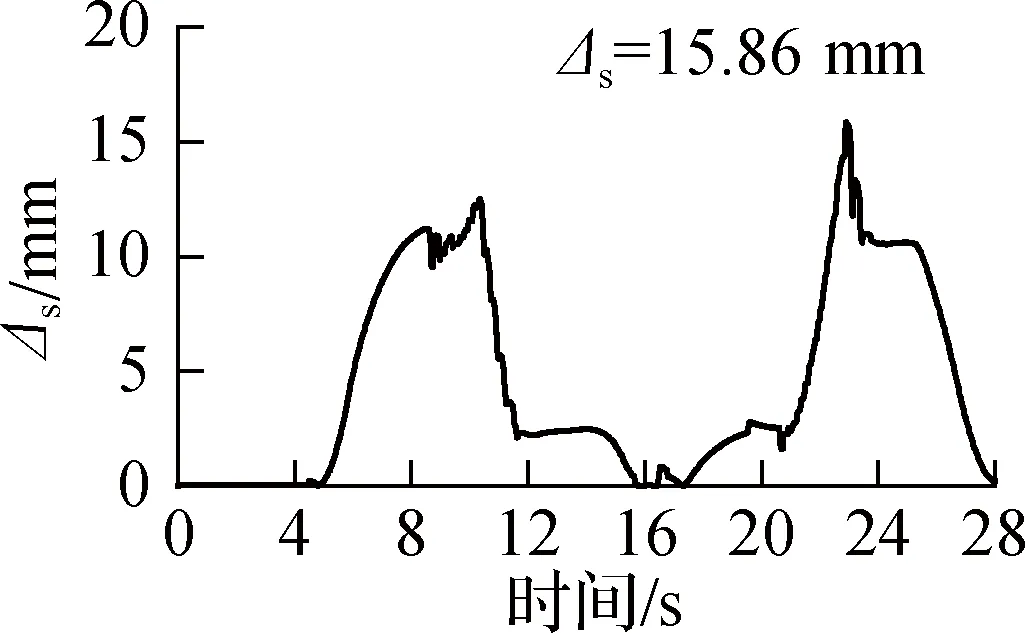
(d) 机器人行进稳定性变化

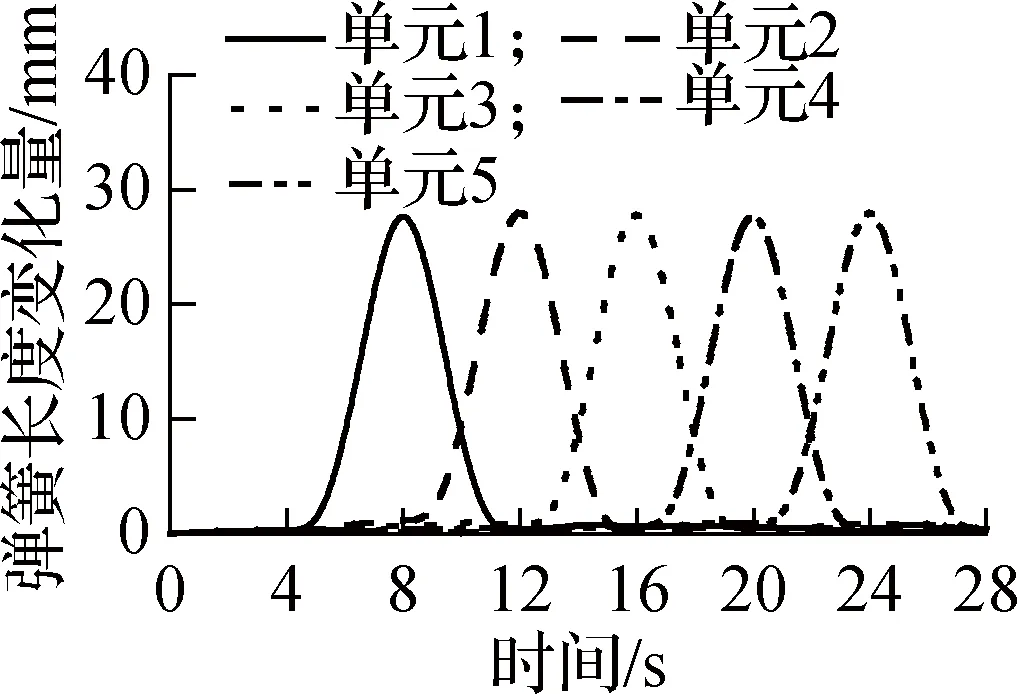
(e) 单元1～5的斜索长度变化图7 张拉整体管道机器人仿真结果

由图7(c)可知,机器人的能量消耗随时间增加而不断增加,在t=28 s时达到1 184.24 J.在驱动过程中,能量消耗与时间基本呈线性关系,即能量消耗与驱动单元的相对位置无关.这表明各单元的驱动杆仅作用于自身单元的折展,基本不作用于其他单元.

由图7(d)可知,稳定性参数Δs=15.86 mm,机器人总高度为170.71 mm,行进过程中最大的高度差约占总高度的9.3%,表明机器人行进过程较为稳定.机器人在t=23 s时达到最不稳定的状态,这是由于星形张拉整体单元的中心构件在伸长的同时,结构径向会产生收缩[16].因此,当机器人头尾单元被驱动时,即t∈[4,12]∪[20,28]s时,由于单元径向收缩会产生悬浮现象,从而导致机器人倾斜;而当头尾单元不驱动时,即t∈[12,20]s时,头尾单元落地,z坐标基本不变,稳定性较好.

由图7(e)可知,各个单元斜索在被驱动时均伸长,伸长量最大值基本相同,约为28 mm,在不被驱动时基本保持原长.同时,所有单元的斜索并未出现缩短的现象,证明了机器人中的索时刻受拉,不会松弛.

通过模拟仿真,初步验证了该构型的张拉整体管道机器人具有在水平方形管道中前进的能力.

3 机器人运动性能参数分析

3.1 模型参数设置

本文所分析的机器人参数为单元高度H、斜索预应力Fp、机器人与管道壁之间的静摩擦系数f1、动摩擦系数f2、驱动时间T、驱动长度e,共6个.参数的取值范围和基本值如表3所示.参数分析过程中,某个参数变化时,其余参数保持基本值不变.对于单元高度H变化以及驱动长度e变化的多种情况,均通过了1.2节的驱动策略可行性验证.

表3 参数变化范围

3.2 仿真结果分析

在所选参数变化范围内,张拉整体管道机器人3个运动性能评价指标的变化趋势如图8所示.从图中可以看出:

(a) 单元高度H

(b) 斜索预应力Fp

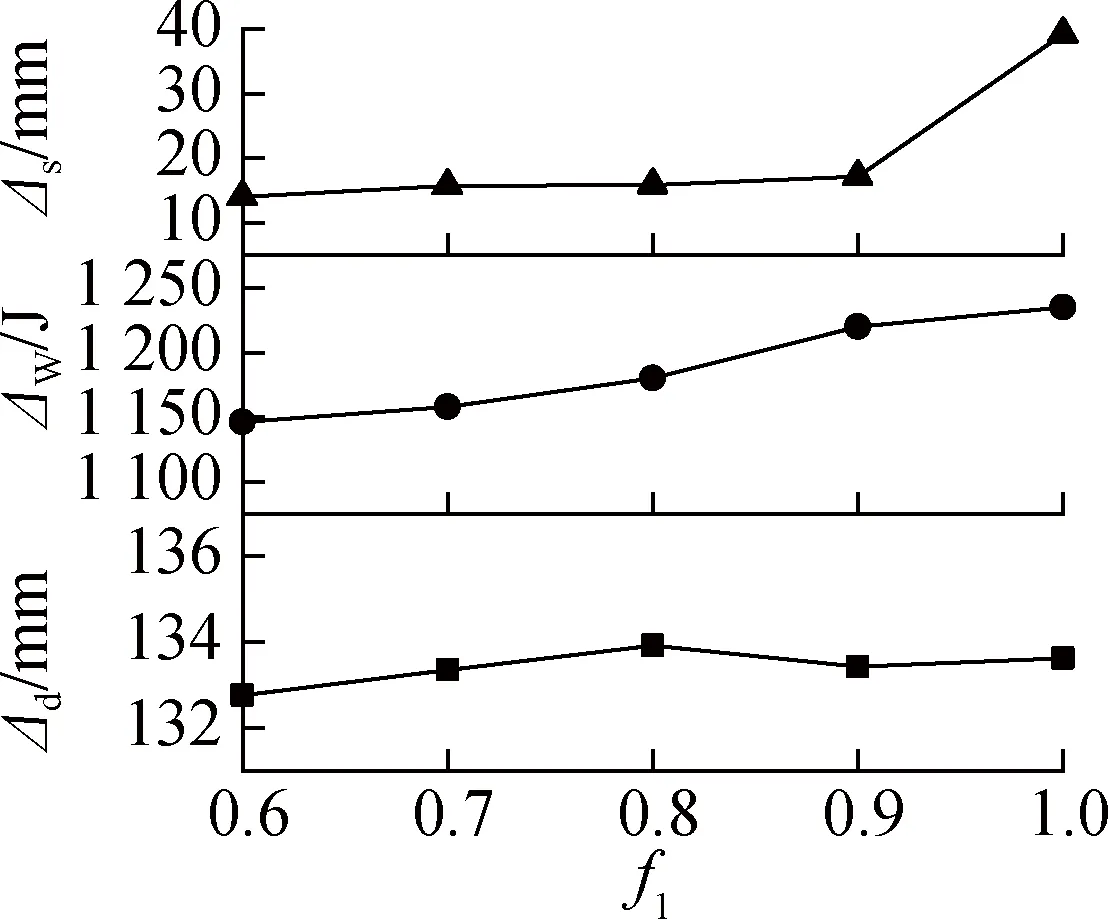
(c) 静摩擦系数f1

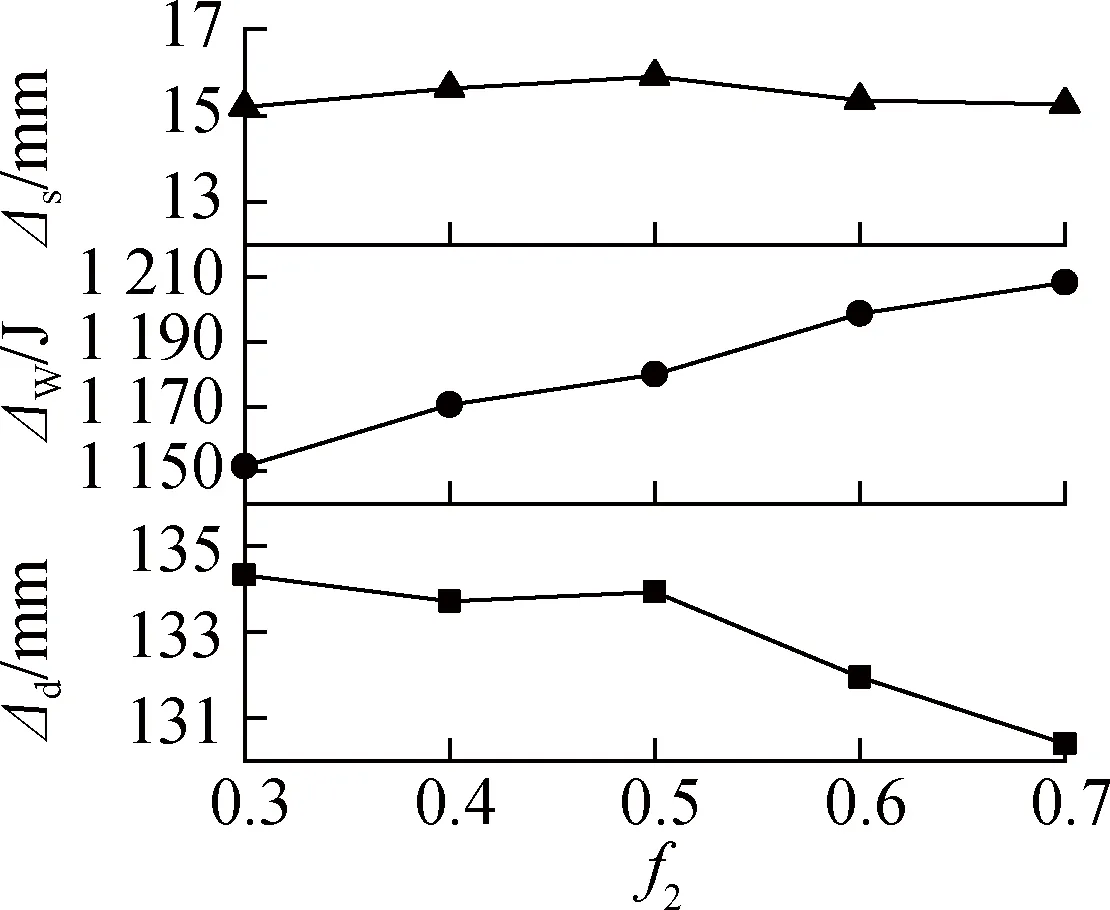
(d) 动摩擦系数f2

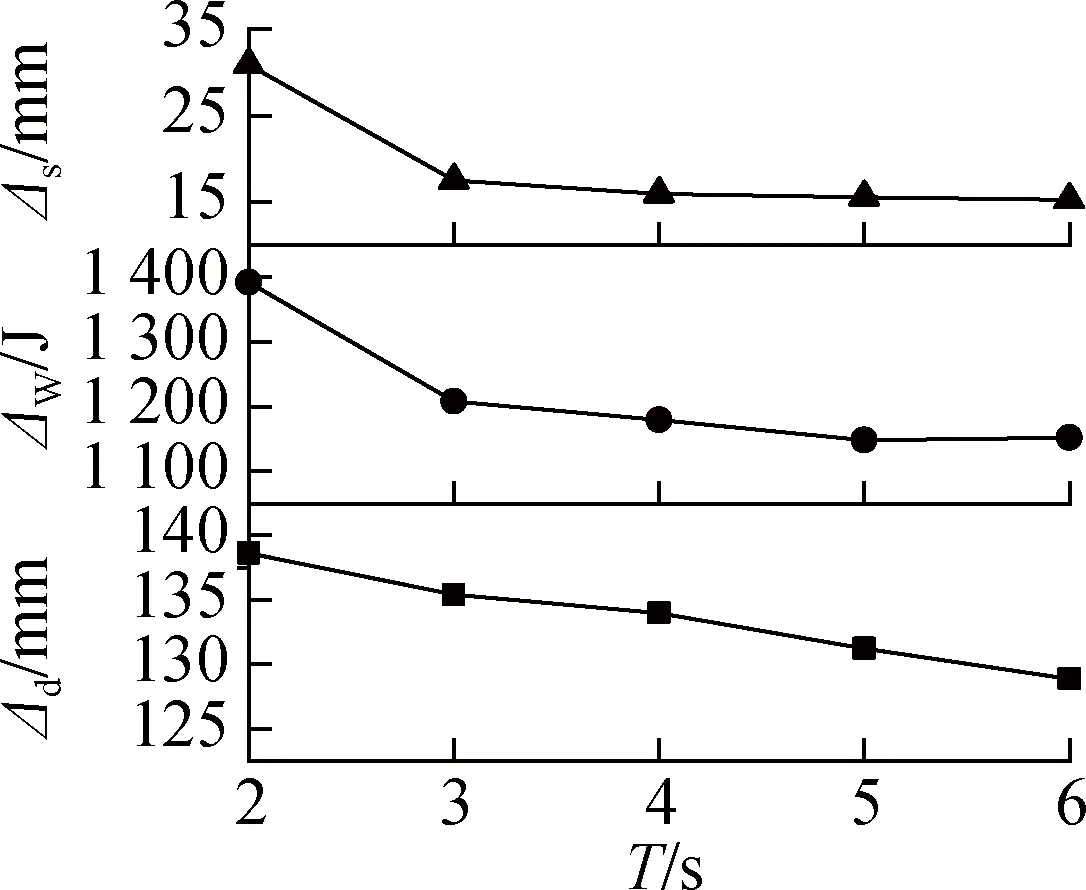
(e) 驱动时间T

(f) 驱动长度e

1) 单元高度H的增大对于Δd、ΔW、Δs三种性能指标的影响不大.

2) 斜索预应力Fp增大时,Δd、ΔW增大,Δs减小.预应力增大导致结构的刚度随之增大[19],机器人受到碰撞等扰动减小,结果更加贴近理论情况,使Δd增大,Δs减小;同时,预应力的增大也会引起中心杆轴力增大,使ΔW增大.

3) 静摩擦系数f1增大时,Δd、ΔW、Δs均增大.静摩擦力能够有效阻止机器人在t=8～28 s内向后滑动,结果更加贴近理论情况,使Δd增大;同时,静摩擦力的增大使机器人受到的阻力增大,从而使ΔW增大;阻力增大也会引起机器人受到约束,约束过大(f1=1.0)时机器人发生扭曲,Δs增大.

4) 动摩擦系数f2增大时,Δd减小,ΔW增大,Δs影响不大.动摩擦力越大,机器人前进时受到阻碍越大,前进距离与理论值之间的误差也随之增大,Δd减小.ΔW分析同静摩擦系数f1.

5) 驱动时间T增大时,Δd、ΔW、Δs均减小.机器人总运动时间增大,阻力做功就会增大,进而导致Δd减小,ΔW增大;同时,驱动时间增大,机器人运动缓慢,因此Δs会减小.

6) 驱动长度e增大时,Δd、ΔW、Δs均增大.根据纵波法运动步态,驱动长度越大,Δd就越大;但驱动长度增大,每个单元的变形就会增大,ΔW必然增大,Δs增大.

3.3 结果讨论

增大斜索预应力Fp、静摩擦系数f1、驱动长度e和减小动摩擦系数f2、驱动时间T均能够提高机器人的前进距离.在驱动长度e=175 mm时,前进距离最大能够提高到158.39 mm.但参数的调整有一定范围,超过限制则会导致能量消耗过大以及稳定性下降.例如,当Fp<10 N、f1>1.0、T<2 s时会使得稳定性下降,导致单元扭曲.当Fp、f1、f2、e过大时,均会导致能量消耗过大.

4 不同工作条件下机器人前进性能

4.1 单元损坏对前进性能的影响

根据纵波法运动步态的形成过程,纵波在机器人中的传递由2个相邻单元完成,一旦有某个单元无法伸缩,波将无法正常传递.如图9(a)所示,当单元3损坏不能伸缩时,波无法从前向后传递,机器人前进量几乎为0.但是,若驱动策略跳过损坏的单元3,波的传递通过单元2、4的伸缩进行,如图9(b)所示,机器人的理论前进距离仍为e.

(a) 不调整驱动策略

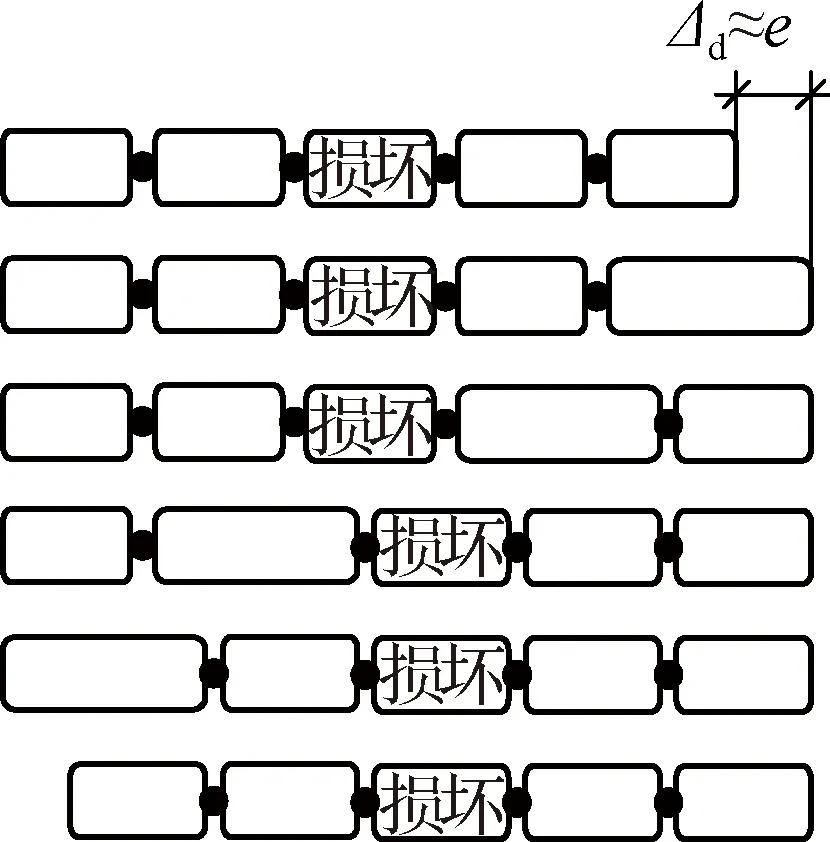
(b) 调整驱动策略

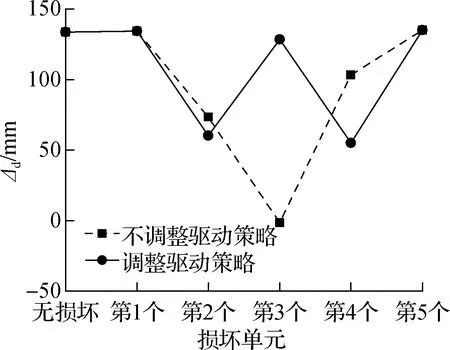
(c) 单元损坏时机器人前进距离

将上述驱动策略输入ADAMS模型中,仿真得到的前进距离如图9(b)所示.由图可知,单元1、5损坏后,机器人的前进距离不受影响,这是因为波能够在首尾单元不参与的情况下传递.若不调整驱动策略,中间3个单元的损坏会中断波的传递,降低机器人的前进距离,甚至停滞不前.若调整驱动策略,在单元3损坏时,机器人的前进距离从-1.58 mm提升至128.3 mm,但仍小于无损坏时的前进距离;在单元2、4损坏时,机器人的前进距离降低至60.09和55.01 mm.这是因为纵波虽然跳过了损坏单元成功传递,但是损坏单元始终与管道壁接触,摩擦力较大,阻碍机器人前进.在波跳过该单元传递时,机器人向后滑动,前进距离下降.相较于单元3,单元2、4在机器人构型中分别位于偏前和偏后的不对称位置,从而下降幅度更大.

整体而言,在1个单元损坏的条件下,虽然前进距离有所下降,但是通过调整驱动策略,机器人仍有继续前进的能力,且前进距离最小为73.41 mm,为原距离的一半以上,具有较好的鲁棒性.

4.2 负重对前进性能的影响

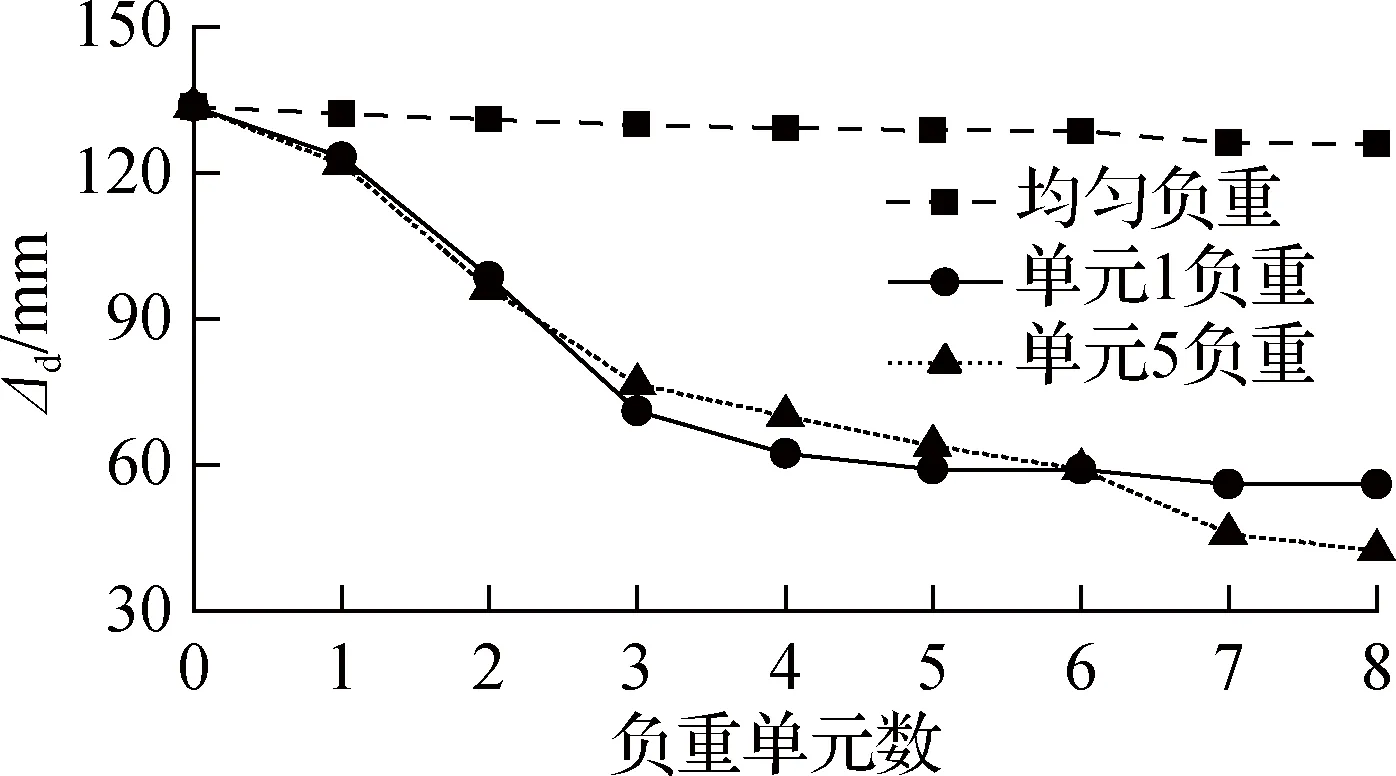
在管道机器人实际应用时,一般需要携带摄像机等装置[1],即负重前进.张拉整体机器人所携带的装置一般绑扎于杆上[9].对于本文机器人构型,斜杆的运动幅度大,中心杆较稳定,因此选择将负重布置在中心杆上.以机器人一个单元的质量为负重单位 (约0.23 kg) ,建立长方体物块,并与中心杆固定连接,通过改变长方体物块的质量来改变负重质量,如图10(a)～(c)所示.为了探究负重位置对于机器人前进性能的影响,分别将负重设置在单元1、5和全部单元上.调整负重质量,仿真结果如图10(d)所示.

(a) 均匀负重

(b) 单元1负重

(c) 单元5负重

(d) 机器人前进距离

由图可知,机器人负重增多,前进距离减小.在全部单元负重时,前进距离能够维持在较高水平,在负重为8倍单元质量时为125.81 mm.而在单元1、5负重时,前进距离下降明显.在负重为6倍单元质量时,即降低至不负重时前进距离的一半,为63.86 mm.

由于负重,张拉整体单元的z向压缩和横向扩张的变形更大.负重均匀分布时,各单元变形基本一致,在两侧管道壁的约束下,前进距离并未急剧下降.负重分布不均匀时,即使有管道壁的约束,前后单元的高度变化不同,机器人发生倾斜,前进距离大幅降低.

整体而言,负重均匀分布时,负重质量对机器人前进性能影响不大;负重不均匀分布时,由于各单元变形不一致,随负重质量增大,机器人前进性能下降明显,应尽量避免.

4.3 管道倾斜对前进性能的影响

很多长直管道并不会始终水平,而是有一定的倾斜角度,因此探究机器人在斜管道中的前进性能很有必要.机器人与管道壁之间的动摩擦系数基本值f2=0.5,机器人理论爬坡的极限角度为θ=arctanf2=26.6°.设置管道倾斜角度范围为0°～25°,其余参数不变,测试机器人前进距离,结果如图11所示.

图11 管道倾斜时机器人前进性能

由图11可知,倾斜角度越大,机器人前进距离就越小.在倾斜角度为10°时,前进距离减小至原来的64%.当管道倾斜角度大于20°时,前进距离为负值.整体而言,机器人在管道倾斜10°以下时保持近一半的前进性能,但坡度较大时,无法在管道中前进.

4.4 管道截面对前进性能的影响

将管道截面改为圆形,测试机器人在圆形管道中的前进性能,圆管的半径为110 mm,略大于张拉整体半径100 mm,其余参数同表2.经过仿真,机器人在管道中前进120.08 mm,如图12所示.相较于方管,机器人在圆管中会发生较多的侧向移动甚至旋转,这会增大机器人前进过程中受到的阻力,降低机器人前进效率.同时,圆管对于张拉整体变形的约束能力小于方管,单元在运动过程中的变形会更大,对于前进也有一定的影响.但是在仿真过程中,机器人并未出现单元扭曲或停滞不前的情况,说明机器人同样可以在圆形管道中前进.

(a) 圆管仿真模型

(b) 机器人前进距离变化

5 结论

1) 基于具有良好折展性能的三杆星形张拉整体,设计出张拉整体管道机器人的构型,并给出纵波法运动步态的驱动策略.ADAMS仿真结果证明机器人可以按照纵波法的运动步态在方形长直管道中平稳前进.

2) 为了提高机器人的前进性能,可以适当增大斜索预应力Fp、增大静摩擦系数f1、减小动摩擦系数f2、减小驱动时间T和增大驱动长度e.但参数的调整有一定范围,超过限制则会导致能量输入过大以及稳定性下降.参数分析为此类机器人的参数设计优选和应用提供了参考.

3) 在管道倾斜角度大于20°时,机器人无法前进;在任一单元损坏时,通过调整驱动策略,机器人仍能保持一半以上的前进距离;负重均匀分布在机器人构型中时,相较于仅单元1或单元5负重的情况,机器人前进性能受负重质量影响较小;机器人在方形和圆形管道中均可以正常前进.