面向超声喷丸的纵弯复合换能器设计与分析

芦小龙 施陆锴 李武琴

(南京航空航天大学航空航天结构力学及控制全国重点实验室, 南京 210016)

喷丸成形技术利用高速丸体冲击金属板件表面,使材料表层重构残余压应力,进而使板件发生向受喷击面凸起的塑性变形,在成形的同时还可改善抗疲劳性能[1-2].其中,超声喷丸作为新型金属冷加工工艺,相较于传统喷丸方法,其可控性更高,加工后的工件具备更高的残余压应力和更小的表面粗糙度[3].超声喷丸的工作介质(弹丸或撞针)在喷丸结束后可进行循环利用,也可有效降低浪费和污染[4].

超声喷丸的成形效果与众多因素相关.Lu等[5-6]从压应力角度描述了电流和撞针直径等因素对成形的影响.Guo等[7]对施加不同喷丸速度的板件变形进行数值模拟,得出喷丸速度与曲率半径的关系.此外,Liu等[8]和Lu等[9]辅以激光或真空的方式对非常规条件下的喷丸成形效果进行了分析.

上述对成形因素的研究均依靠单一纵振的超声换能器,然而对于涉及有限空间的腔体内部超声喷丸处理可实施性较低.利用换能器的纵振模态带动工作介质会受限于轴向尺寸而难以进入较小空间,弯振模态则避免了这个难题.纵弯复合换能器在许多领域内得到了应用.陈一博[10]结合斜槽式细杆设计了一种斜槽式纵弯复合振动夹心式压电超声换能器,实现了换能器的纵弯复合振动.李华等[11]将纵向振动换能器和薄球壳相结合,设计了一种纵弯转换球面弯曲振动聚焦系统,使得纵向振动换能器的超声振动转化为球壳的弯曲振动.

针对现有超声喷丸设备无法加工腔体内部的问题,本文提出一种利用单、双极化压电陶瓷相结合的纵弯复合超声喷丸换能器,通过激励单、双极化陶瓷实现纵振和弯振,以实现加工不同板件的喷丸成形.首先,采用COMSOL软件对换能器进行模态仿真,改变尺寸参数使得工作端面呈现较大振幅.其次,对装配换能器进行串联电感匹配.最后,通过对厚度为10 mm 的2024-T351板件进行超声喷丸处理,从弧高和残余应力角度验证了纵弯复合喷丸技术的可行性.

1 换能器仿真分析

1.1 基本结构

纵弯复合超声喷丸换能器主要包括压电振子和变幅杆,如图1(a)所示.前盖板内侧为螺纹通孔,后盖板内侧为光孔,通过预紧螺钉将压电陶瓷压紧.同轴线的压电陶瓷相对极化方向相反,与后盖板相邻的2片压电陶瓷为单极化,剩余4片为双极化.变幅杆前后两端均为螺纹盲孔,分别与压电振子和纵振垫板螺纹连接.单、双极化压电陶瓷受到正弦高频交流信号激励时,由于逆压电效应促使垫板端面产生振动.喷丸枪结构以及2个工作模式如图1(b)所示,换能器的纵向和弯曲振动带动撞针实现喷丸冲击.

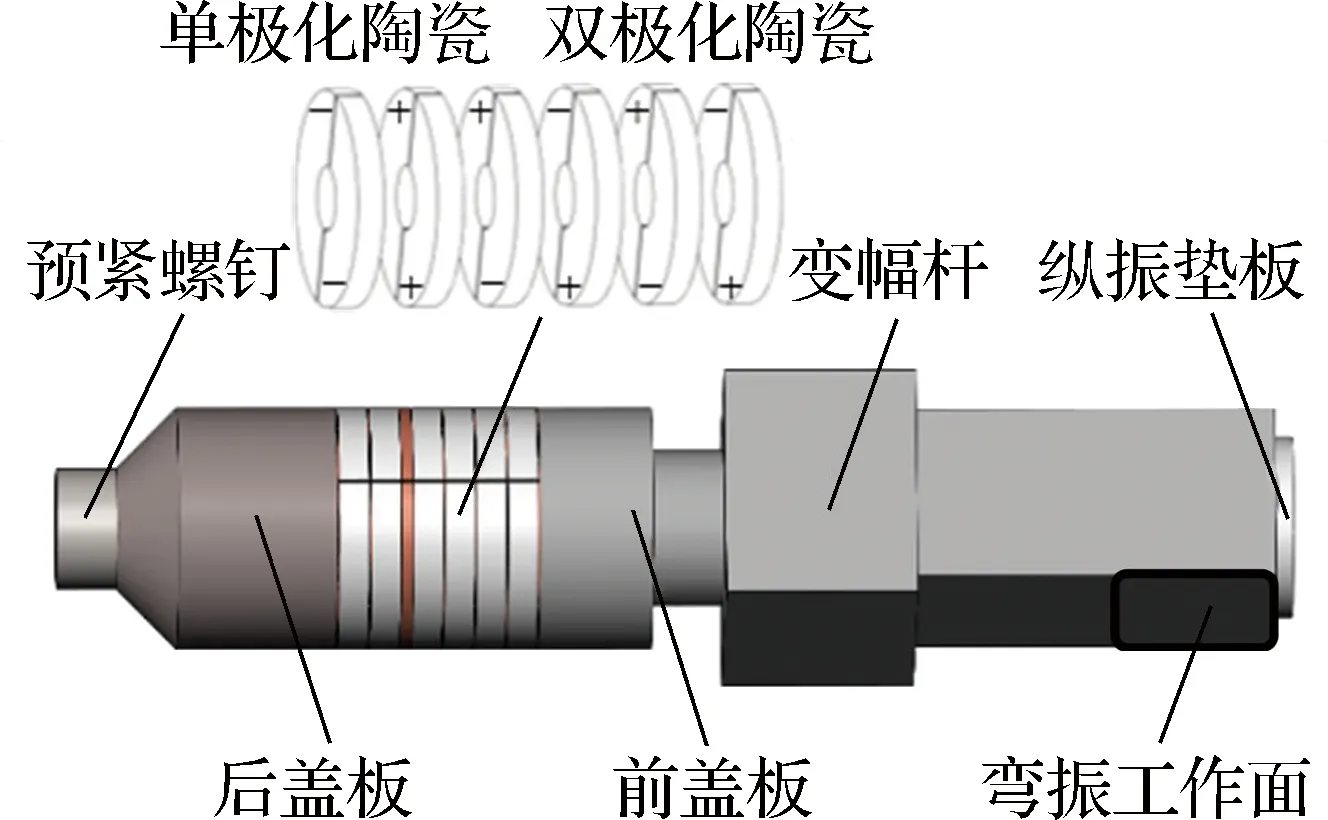
(a) 换能器构型

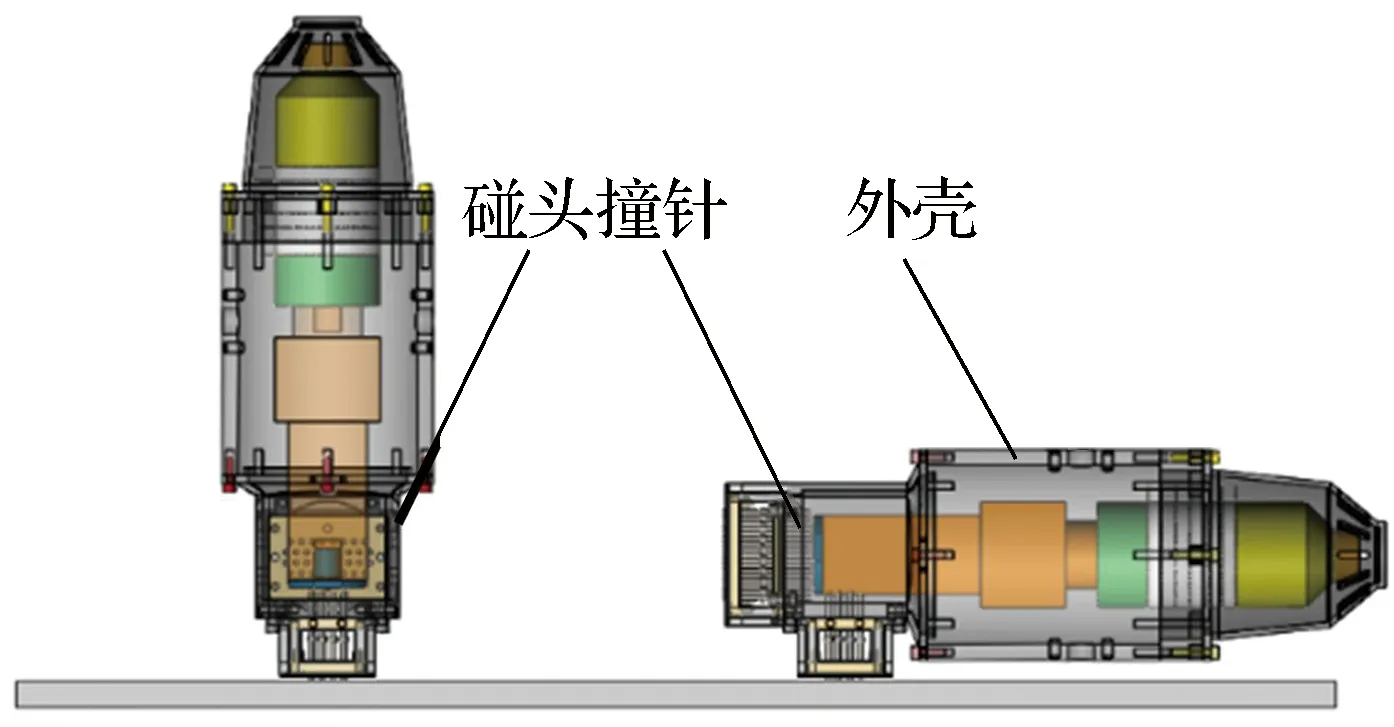
(b) 喷丸枪外形

1.2 模态分析

本文采用COMSOL仿真软件对换能器模态进行了仿真计算.首先对换能器特征频率进行分析,然后在计算的所需模态频率的基础上进行频域分析,并调整尺寸使得换能器在纵振、弯振2种模态下工作端面均实现较大振幅.

仿真物理场选择压电多物理场耦合,分别包含固体力学物理场与静电物理场.省略换能器各零部件间连接部分的螺纹以及接线等,并将换能器设置为各部件的联合体.考虑到换能器工作时需承受撞针喷丸冲击板件后的反弹,采用刚度较大的PZT-8型压电陶瓷作为振子的材料,其密度为7 600 kg/m3,压电常数d33为243 pC/N.选用厚度为5 mm且内、外径分别为15 和40 mm的压电陶瓷作为核心元件,由此设定前后盖板外径均为40 mm,而轴向尺寸以及变幅杆各段尺寸均可调整.换能器其他零部件材料及其密度如表1所示.

表1 不同部件材料及其密度

换能器纵振和弯振2个模态的振型分别由单、双极化压电陶瓷独立激发产生,因此施加的静电条件和谐振频率并不相同,特征频率以及频域分析需分开计算.如图2(a)所示,将极化方向相反的2片单极化陶瓷相邻面设定为U+,两侧设定为U-,特征频率求解区间为10～30 kHz.计算得到所需模态的特征频率后,通过频域分析计算所需模态特征频率下的换能器工作端面振幅.多次优化尺寸后的频域计算结果表明,当激励频率为22.524 kHz时换能器呈现二阶纵振.以上述换能器各段尺寸为基础计算弯振模态时工作端面振幅,结果如图2(b)所示.由图可知,同侧相邻半片陶瓷极化方向相反,最外侧和中间设定为U-,其余设定为U+.当激励频率为12.600 kHz时换能器呈现三阶弯振.此时,纵振压电陶瓷与弯振压电陶瓷均位于最佳励振位置.与前盖板接触的变幅杆圆柱段直径为26 mm,其余2段截面为方形,边长分别为40 和30 mm.换能器各段的轴向尺寸如表2所示.

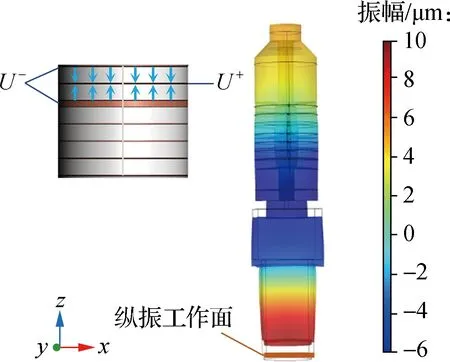
(a) 纵振模态

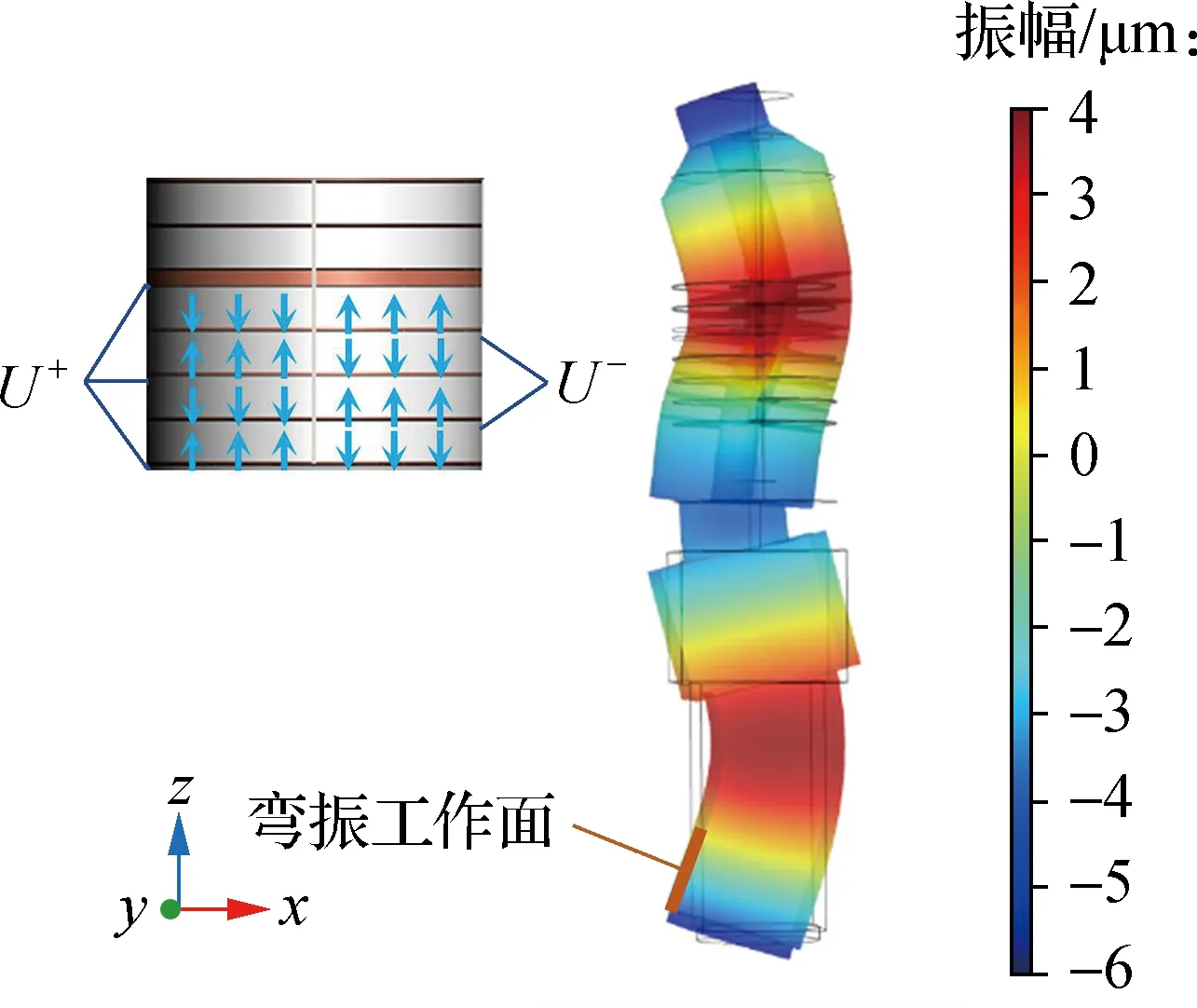
(b) 弯振模态

表2 不同部件的轴向尺寸

2 性能测试

按照1.2节模态分析所得的结构尺寸(见表2)进行加工装配,由于压电陶瓷抗拉强度低,且为了更好地传递振动,在后盖板施加19.6 kN压力后以50 N·m的扭矩旋紧预紧螺钉.装配完成的换能器如图3所示.

图3 超声喷丸换能器实物

采用激光多普勒测振仪分别对换能器的2个工作端面进行测振.设置扫频区间为10～30 kHz,激励电压为100 V,结果如图4所示.纵振工作面如图4(a)所示,垫板端面在10～30 kHz内出现多个振速峰值.在fs1处出现最大振速,且与仿真结果最为接近.以fs1进行定频分析,该端面最大振幅为1.0 μm.弯振工作面如图4(b)所示,变幅杆端面也在区间内出现多阶弯振振模态,以fs2进行定频分析,该端面最大振幅为0.8 μm.

(a) 垫板端面纵振工作面

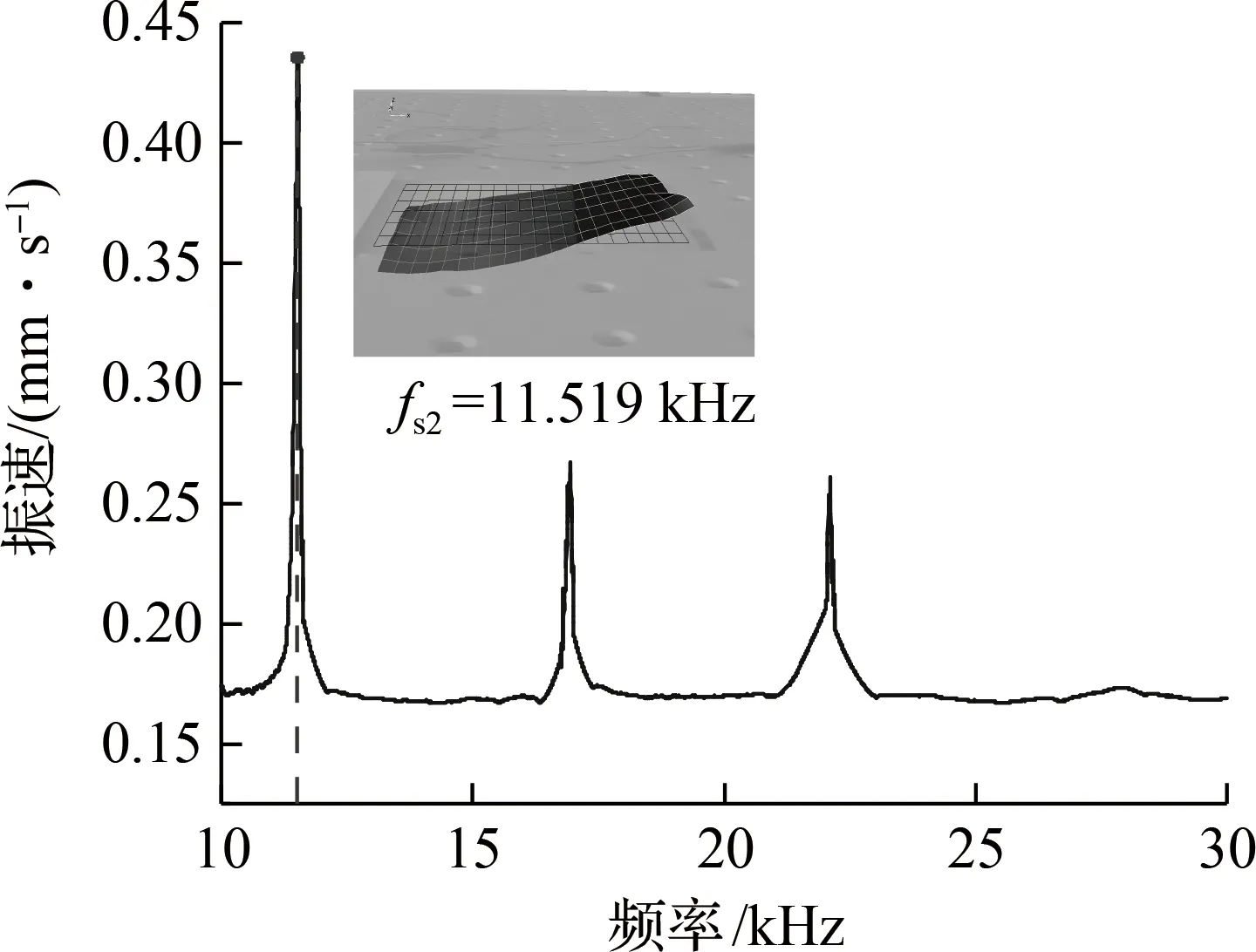
(b) 变幅杆端面弯振工作面

对于单一振动模式的换能器,谐振频率附近的等效电路为并联电容C0、动态电感L1、动态电容C1和动态电阻R1的串并联[12],如图5所示.而处于谐振状态下的压电换能器,其支路上L1和C1互相抵消,等效为阻容元件的并联,对外呈现为容性[13].由于谐振频率附近换能器等效元件变化极大,因此难以精确获取换能器阻抗值,可将其等效为容性元件Ca和阻性元件Rb的串联[14-15],并用串联电感Ls补偿使得负载电路呈现阻性.

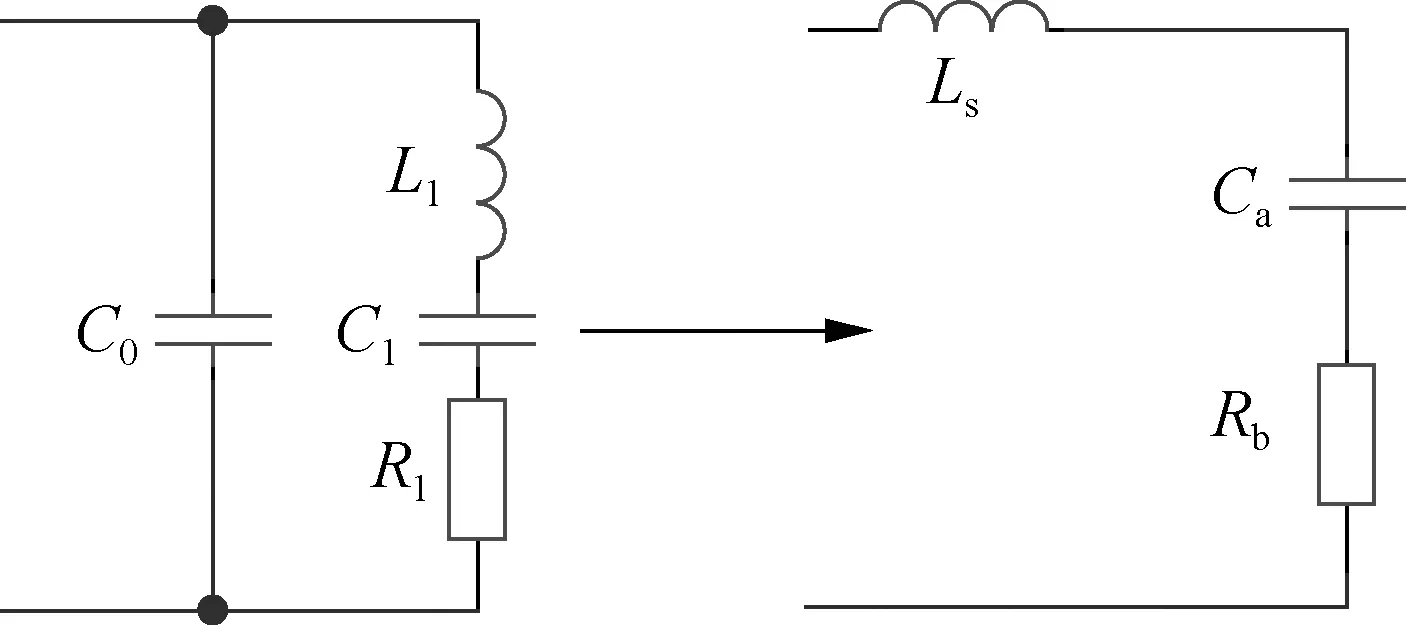
图5 换能器等效电路及匹配方式

利用示波器测得换能器实际工况下的电压峰值Umax、电流峰值Imax和2路信号之间的时间差ΔT.阻抗计算公式如下:

(1)

φ=ΔT×f×360°

(2)

Re=ZTcosφ

(3)

Im=ZTsinφ

(4)

ZT=Re+Imj

(5)

式中,ZT为超声换能器阻抗,Ω;f为换能器实际工况下的频率,Hz;φ为电压电流的相位差,也是超声换能器的阻抗角,(°);Umax为电压峰值,V;Imax为电流峰值,A;ΔT为电压信号和电流信号的时间差,s;Re为阻抗实部,Ω;Im为阻抗虚部,Ω.

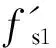
(6)

计算得到纵振模态的匹配电感理论值为3.1 mH,弯振模态匹配电感理论值为14.1 mH,并在此基础上微调电感,负载电路的阻抗结果如图6所示,图中,Zin1、Zin2分别为纵振模态和弯振模态的阻抗.换能器在匹配后呈现阻性,工作端面纵振模态和弯振模态的最大振幅分别提升至1.4和1.2 μm,分别增长了40%与50%.

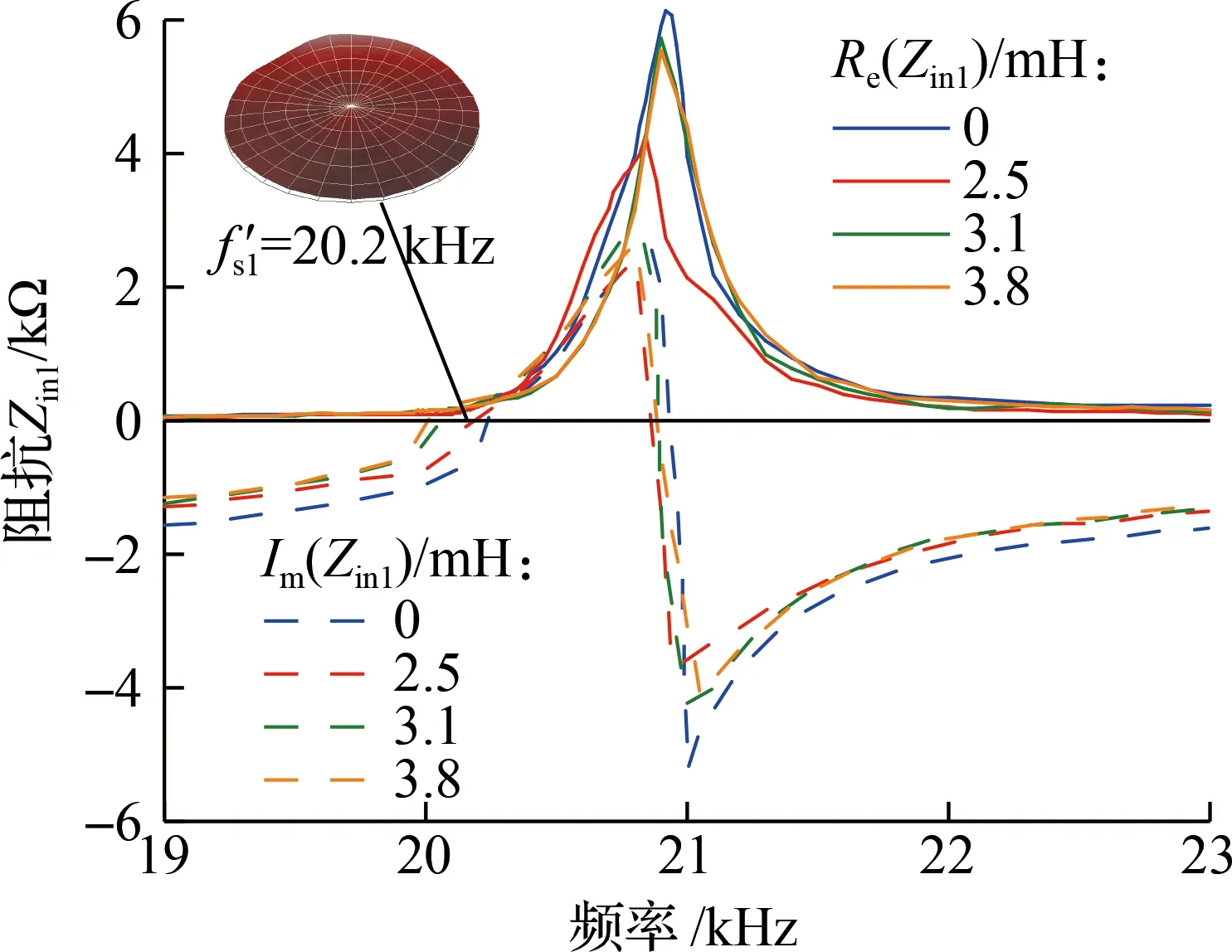
(a) 纵振匹配

(b) 弯振匹配

3 喷丸试验

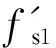
(a) 碰头构型

(b) 撞针尺寸(单位:mm)

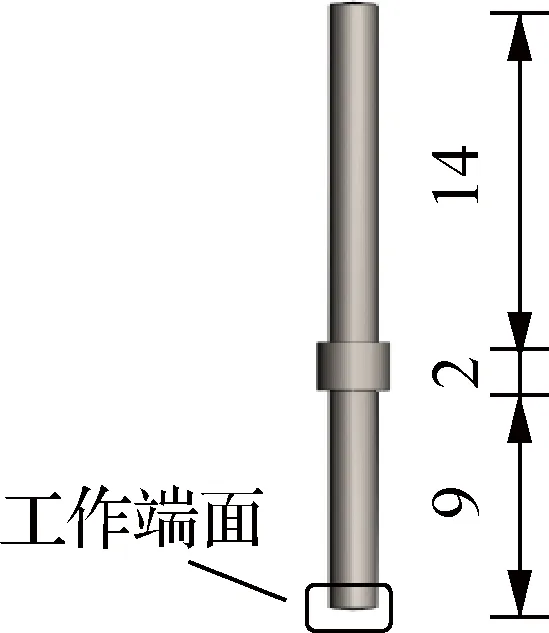
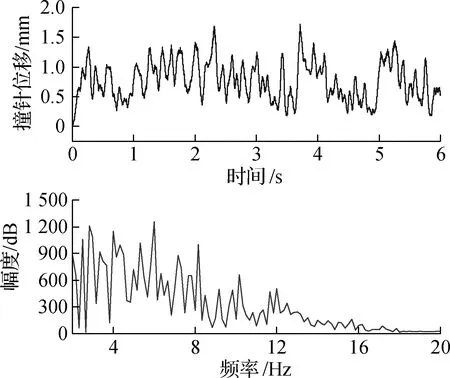
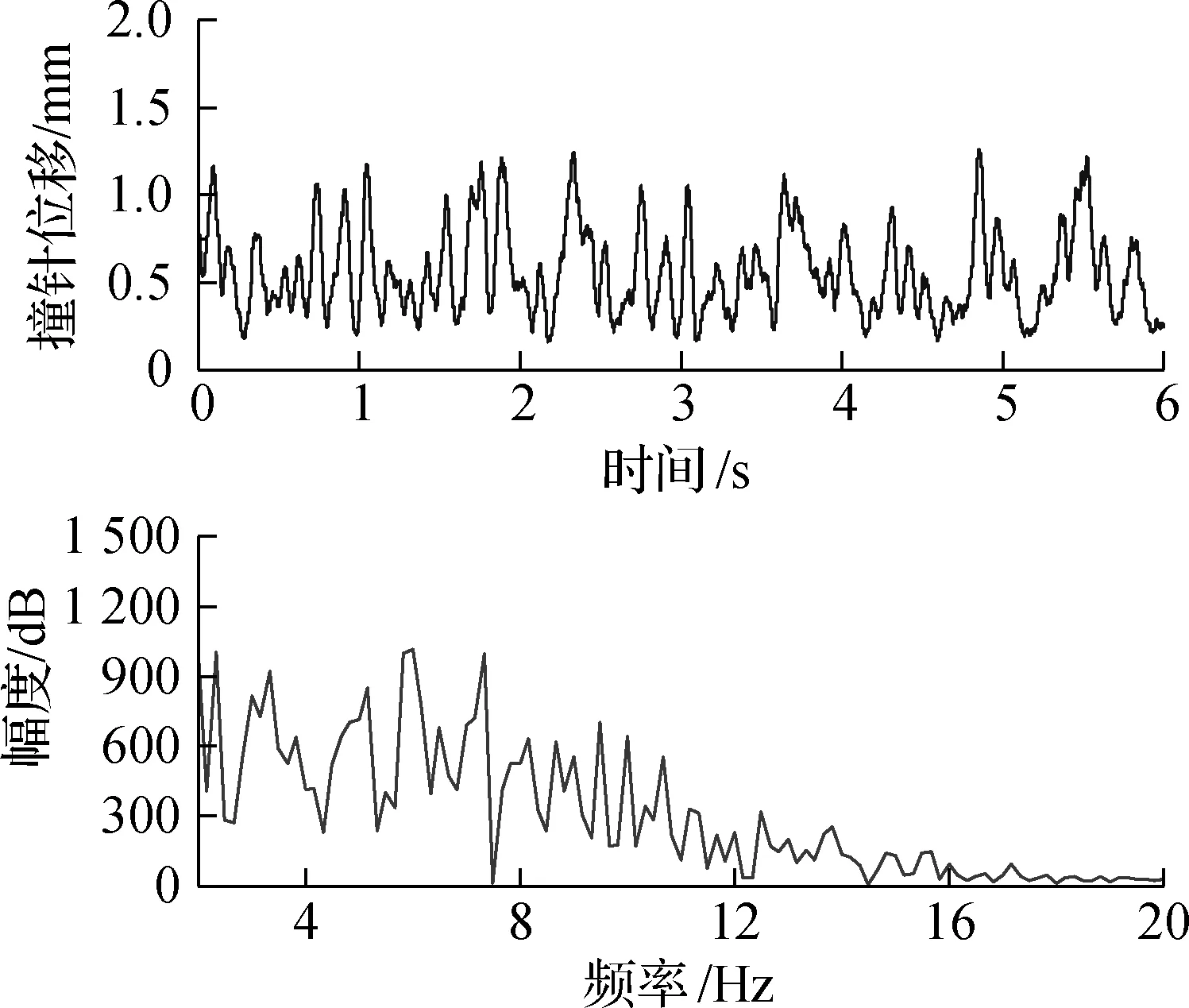
利用激光位移传感器记录纵振和弯振2种模态下撞针的位移,采样周期为0.2 ms. 撞针运动轨迹如图8(a)和(b)所示.由图可知,撞针冲击频率均远小于激励信号频率,恢复周期不等,且位移幅值在不同恢复周期内呈现波动.在记录的6 s内,纵振端面的撞针最大位移达到1.7 mm,而弯振端面的撞针最大位移达到1.3 mm.

(a) 纵振模态

(b) 弯振模态

喷丸枪碰头通过外壳与换能器相装配,需确保2个工作端面均能抵住该方向的撞针.图9为喷丸枪样机的纵弯操作模式.

(a) 纵振喷丸

(b) 弯振喷丸

选取常见的航空壁板材料2024-T351作为试验件,板件尺寸为800 mm×50 mm×10 mm,两端由夹具固定,沿长度方向进行喷丸,时间为15 min.板件成形结果如图10所示.纵振喷丸最终弧高为0.64 mm,而弯振喷丸最终弧高为0.55 mm.这一方面是由于弯振工作端面的撞针越远离变幅杆末端,振幅越小;另一方面是因为纵振工作端面的撞针位移本就大于弯振.基于X射线法对残余应力进行测试,结果如图11所示.由图可知,受喷工件表面在约100 μm深处残余压应力达到最大值,约为250 MPa,改善了板件的抗疲劳破坏能力.

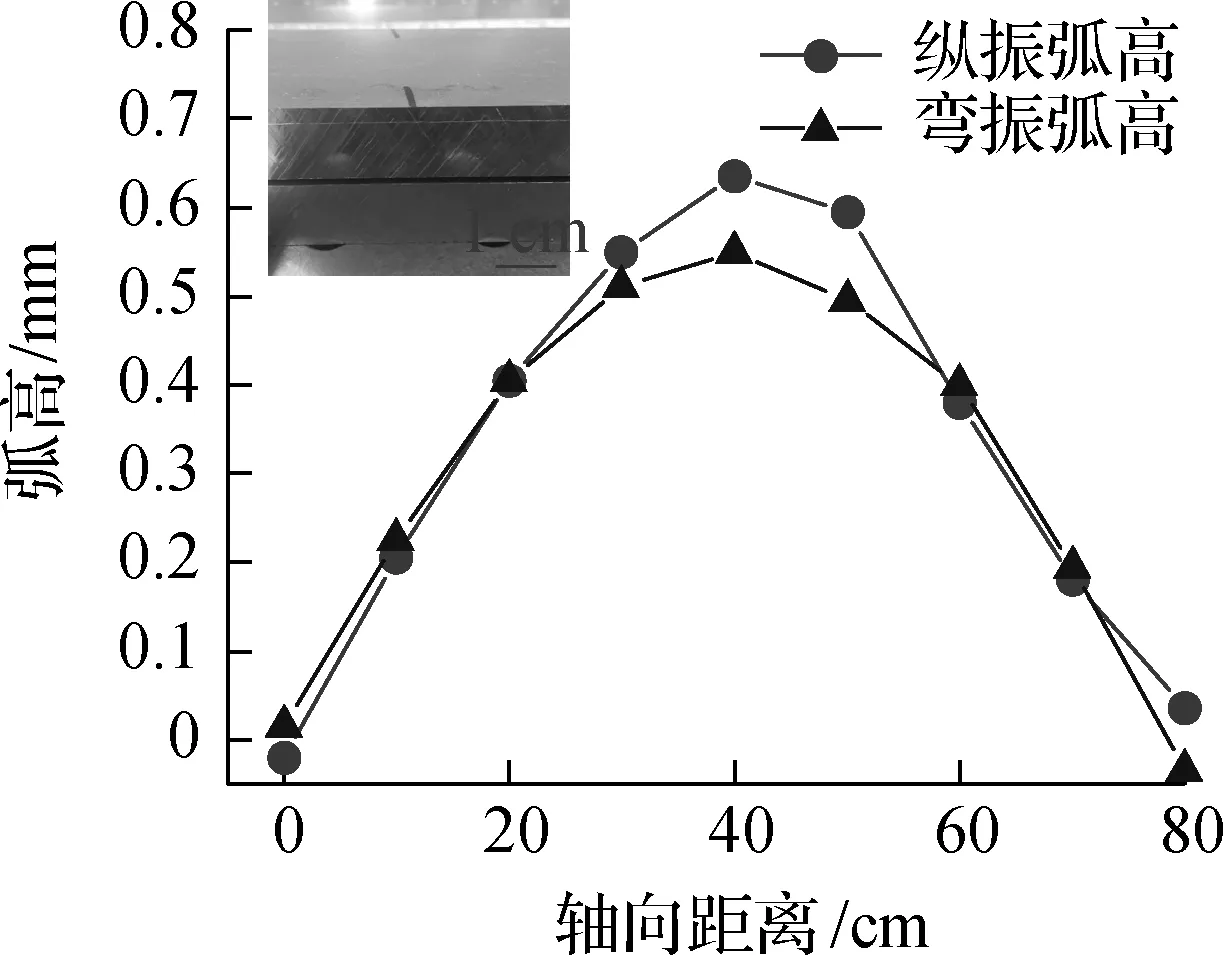
图10 喷丸成形弧高变化曲线

图11 纵弯喷丸工件残余应力曲线

4 结论

1) 利用压电陶瓷的逆压电效应,采用单、双极化压电陶瓷,设计了一款纵弯复合模态的夹心式压电换能器,借助COMSOL软件对换能器模型进行了仿真分析.分析结果表明,换能器在不同频率下分别表现出二阶纵振模态和三阶弯振模态.

2) 采用激光多普勒测振仪对换能器2个模态下的工作端面进行测振.测试结果表明,换能器仿真和实物测试共振频率相差不超过2 kHz,且经匹配后实物2个模态的工作端面振幅与未匹配前相比,分别增长了40%和50%,表明匹配能起到增大换能器振幅的效果.

3) 利用激光位移传感器测试2个模态下的撞针位移,在相同激励电压下,纵振模态下的撞针位移略大于弯振模态.通过搭建的喷丸试验平台对喷丸枪2个模式的校形效果进行了验证,并利用X射线法测试了板件的残余应力.试验结果表明,纵振和弯振喷丸模式均可使得板件发生弯曲,但纵振模式对板件产生的弧高和残余应力值都更大.