基于动态择优组合的板材切割下料算法

鞠云鹏 ,常德功

(青岛科技大学a.自动化与电子工程学院;b.机电工程学院,山东 青岛 266061)

随着板式家具的批量生产,采取何种优化的板 材下料方法以提高板材利用率、降低产品的定制成本,成为企业竞争的关键所在[1-4]。计算机辅助排样方法能够提高排板精度,将低人工费用,减少误操作,提高板材切割效率[5]。将一批不同尺寸规格的板件排列在大的板材上并达到高的板材利用率是一个复杂问题,并且不确定能否在多项式时间内找到答案[6]。应用常规方法来解决这类多项式不确定性问题,所用时间达不到现实要求。对于生产规模较小的企业,可以使用早期板材切割下料的一些方法[7-11]。但随着板式家具的批量定制,很多企业的产量已达不到市场需求,同时板材切割利用率低的问题也开始暴露。针对低效率、低利用率问题,一些新的算法被先后提出。最下最左算法[12]首先被提出,之后在此基础上出现了下台阶算法[13],后来又出现了最低水平线算法[14-15]以及近似算法[16]。以上几种方法相对于传统排样方法具有明显优势,但不能对所有矩形件进行全局搜索,因此,其具有一定局限性。随着GA、SA、TS、AA、ANN 等智能算法的发展,出现了智能算法与常规算法相结合的优化算法。文献[17]将蚁群算法与启发式算法相结合,来优化板材切割下料。文献[18]依据模拟退火局部搜索能力强、收敛速度慢和遗传算法全局搜索能力强、收敛过早的特点,将二者进行有效结合。通过智能算法寻优,对于不确定性排板问题可以更大范围的搜索有效解。对于数量较大、尺寸差异、规格不一的板件排样,遗传算法能够在更大的范围空间内进行寻优,但搜索有效解的时间会变长[19]。相对于最低水平线算法,最低水平线搜索算法在一定范围内进行了寻优,但需对换两个矩形件的位置,造成后面排板过程中小件缺失。本研究在最低水平线搜索算法基础上,首先,将待排板件按面积大小进行排列。其次,在最低水平线排放矩形件时,按照矩形件的长度或宽度所占据最低水平线的比例来选取。若组合占据的比例较大,则优先选取矩形件组合进行排放,并且组合中矩形件不能与其它待排矩形件交换顺序。通过对矩形板件进行排样,此优化组合算法能够有效提高板材的利用率。

1 数学模型

整块矩形大板的长、宽分别为L、W,为减少切割过程所产生的余料,应尽量使所排放板件之间的空隙减到最小。设待排板件的规格数为k,第i 种板件的个数为ni,宽、长分别为wi,li。大板数量充足,则待切割小板件的数量可表示为

板件排放过程中可按长边进行排放,也可按短边进行排放,这需根据板件有无纹理加工要求进行。第一块板件应首先放置在大板的左下角,并且后面板件要排放均匀。设大板左下角为基准点,第i 块板件左上角的坐标表示为(x1i,y1i),其右下角的坐标表示为(x2i,y2i)。根据板件按长边或短边的排放形式,其对角线上两点的坐标可表示为

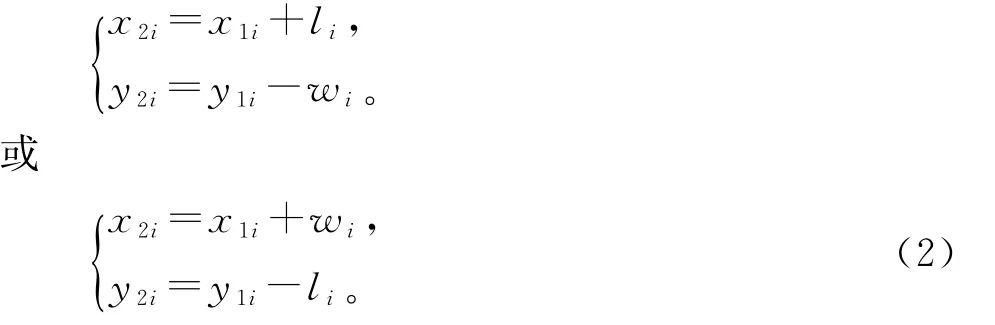
ri＝0、1,当板件按长边进行排放时,ri取0。当板件按短边进行排放时,ri取1。建立板件左上角坐标与右下角坐标的关系:

为提高板材的利用率,板材上板件间的距离应尽量小,但板件排放时不能重叠、不能压边。取任意两个板件Rt、Rs,为满足排放要求,需满足坐标关系。根据式(3)可得

板件在排放时,除满足板件间不能重叠、压边外,还应保证板件不能排到大板边界之外,即板件右下角横坐标小于板件长度,板件左上角纵坐标小于板件宽度。根据以上约束可得

式(5)中u 为单位阶跃函数。为使板材利用率最高,应满足式(6)目标函数。

一般Sj为定值,代表一批板材中大板的面积;Sm为一次生产中所用最后一块大板的面积。

2 优化组合算法分析

本工作以启发式定位算法为基础,并对数据库中待排件逐一进行面积计算,然后按面积大小进行排序。采用动态择优组合算法对其进行排放。假设最低水平线长度为l,板件的排放顺序如下。

1)选择待切大板的底边作为最低水平轮廓线,使其成为集合元素。

2)从待排矩形件中搜索矩形件或矩形件组合,搜索原则按照矩形件或矩形件组合占据最低水平线的比例来确定。若存在多个组合,则按照面积大小优先选取面积较大的组合。

3)在所建立的集合中查找最低水平线,并比较组合件底边长度与l:①如果组合件底边长度较短,则组合件可放置在该水平线。如果组合件底边长度大于l,但宽度小于l,且板件没有纹理切割要求,那么此组合件经旋转后可放置在该水平线。如果该组合件的长度不等于其宽度,并且长、宽均小于l,且板件没有纹理切割要求,则将该组合件按长边放置在该水平线。②否则在待排放的矩形件序列中,将其它组合件的长、宽与l进行比较,当搜索到合适的组合件时,不互换当前不能排放的矩形件与所搜索到的组合件的位置,而是只将搜索到的组合件放置在当前最低水平线。如果组合件的长、宽均大于l,则最低水平线需调整至一定高度,此高度应与该水平线相邻的其它最低轮廓线的高度保持一致,同时最低轮廓线集合也需进行更新。

4)重复执行程序第2)、3)步,一块大板被切割完成后,需用另一块大板,此时再从程序第(1)步开始执行。本工作将此算法称为动态择优组合算法。

3 比较分析

3.1 下料数据

为更好的验证优化组合算法对排板的有效性,本文以工厂实际提供的下料板件数据为实验数据。板材采用常用的2440×1220×18 规格,单位为mm。下料板件的尺度及纹理要求如表1所示。

表1 板件明细Table 1 Details of the board

3.2 排板算法比较与分析

3.2.1 最下最左算法

图1为最下最左算法排版。对板件{＋1,＋2,＋3,＋4}进行顺序排放,数字前的“＋”表示板件不能旋转。根据最下最左规则,排放完板件1、2、3后,板件1、2与板件3之间产生了大的空隙(图1(a))。再继续对板件4进行排放,板件4排放完成之后,仍然没有弥补前面留下的空隙(图1(b))。4个板件较为理想的排放形式如图1(c)所示,其板件的排放较为紧凑。

图1 最下最左算法排板Fig.1 Bottom left algorithm layout

3.2.2 下台阶算法

对板件{＋1,＋2,＋3,＋4}进行顺序排放,此节中的板件区别于图1中的板件,数字前的“＋”表示板件不能旋转。将最下最左算法的排板与下台阶算法的排板进行比较,见图2。对前3个板件的排放,二者均没有明显优势(图2(a))。对第4个板件进行排放时,出现了差距,最下最左算法没有将板件放置在最低轮廓线上,造成整体排放高度较高,而下台阶算法整体排板较为均匀,板件排列紧凑。

图2 BL算法与下台阶算法排板对照Fig.2 Comparisons between BL algorithm and lower step algorithm

3.2.3 最低水平线算法

最近水平线算法见图3。对板件{＋1,－2,＋3,＋4}进行顺序排放,此节中的板件区别于前面的板件,数字前的“＋”表示板件不能旋转,“－”表示板件旋转90°后排放。图3中(a)～(f)是根据最低水平线法对4个板件的排放过程。

图3 最低水平线算法排板Fig.3 Lowest horizontal line algorithm layout

分别采用最低水平线法和下台阶算法对6个板件的排板效果进行比较见图4。对前5个板件的排放,二者均没有明显优势(图4(a))。对第6个板件进行排放时,二者出现了差距。最低水平线法将板件6安置在了最低轮廓线处,下台阶算法将板件6安置在了比最低轮廓线高的板件4之上,造成下台阶算法的整体排板高度较高,排板不均匀,而图4(b)的排板效果较为理想。

图4 最低水平线法与下台阶算法排板对照Fig.4 Comparisons between the lowest horizontal line method and the lower step algorithm

3.2.4 最低水平线搜索算法

对图3中4个板件进行排放,采用最低水平线法对板件3排放时,由于板件3长度大于当前最低水平线,因此,板件3不能放在最低水平线gd,此时需更新最低水平线,新的最低水平线变更为ab,然后对待排板件进行排放。根据最低水平线搜索算法规则,当板件3不能排放在gd时,可从待排件中选出适合排放的板件4,这样就避免了最低水平线以上部分排放空间的浪费。将最低水平线搜索算法与最低水平线法进行比较见图5,图5(b)较图3(f)的整体排板更低、更均匀。

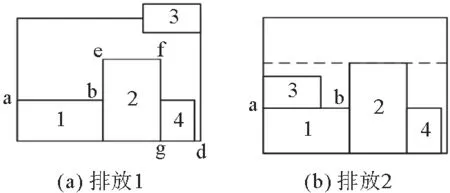
图5 基于最低水平线搜索算法排板(对照图3)Fig.5 Layout based on the lowest horizontal search algorithm(comparative Fig.3)

3.2.5 动态择优组合算法

对板件{－1,＋2,－3,＋4,－5,＋6,－7}进行顺序排放,此节中的板件区别于前面的板件,数字前的“＋”表示板件不能旋转,“－”表示板件旋转90°后排放。根据最低水平线搜索算法规则对7个板件进行排放见图6,当第4个板件进行排放时,出现了板件4长度大于当前最低水平线的情况,为此采用搜索算法,选择了合适的板件7,并将合适板件与不合适板件的位置进行了交换。再对板件5、6、4进行排放,造成图6(c)的整体排板高度较高,板件2、3、4、6间留有大的空隙。区别于最低水平线搜索算法,根据动态择优组合算法规则对7个板件进行排放见图7,在找到合适的板件7之后,将其安置在当前最低水平线处。然后再对板件4、5、6进行排放,效果如图7(b),通过图得知,其排板均匀、整体高度低,较图6(c),其利用率更高。

图6 基于最低水平线搜索算法排板(对照图7)Fig.6 Layout based on the lowest horizontal search algorithm(comparative Fig.7)

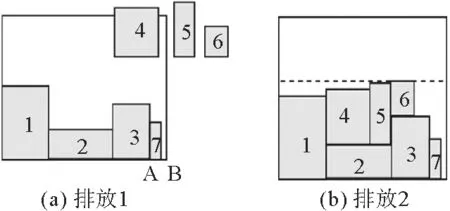
图7 动态择优组合算法排板Fig.7 Dynamic optimum combination algorithm layout

为验证动态择优组合算法的排板效果,选用表1中实际切割板件作为优化组合排列对象。同时,采用最低水平线搜索算法对实际切割板件进行排列(图8),与动态择优组合算法(图9)形成对照。表2为板材利用率表。

表2 板材利用率Table 2 Utilization rate of raw materials

图8 基于最低水平线搜索算法排板(对照图9)Fig.8 Layout based on the lowest horizontal search algorithm(comparative Fig.9)

图9 基于动态择优组合的矩形件排板Fig.9 Rectangular parts layout based on dynamic optimal combination

分别采用以上两种方法对表1中不同规格的板件进行排板,通过图8、图9得知,采用动态择优组合算法比最低水平线搜索算法少用1张大板,采用优化组合方法能够明显提高板材的利用率。表2统计了优化组合方法下6张大板各自的利用率。

4 结 语

对于板材切割下料问题,最下最左算法、下台阶算法、最低水平线算法、最低水平线搜索算法具有一定的优势,但以上算法的适用范围较窄,为此采用基于动态择优组合的板材切割下料算法。通过实验板件所用大板的张数可以证明基于动态择优组合的板材切割下料算法更能提高板材的利用率。