用于路面纹理指标计算的点云坐标校正方法

朱乐毅 黄晓明 罗浩原 马 涛

(东南大学交通学院, 南京 211189)

(东南大学道路交通工程国家级实验教学中心, 南京 211189)

路面的抗滑性能是公路建设与运营管理中评价安全性的重要指标之一.基于摩擦学分析和试验统计学,许多研究建立了路面的纹理指标与路面-轮胎摩擦系数以及路面抗滑指标间的相关关系[1-6].近年来,CT扫描、光学成像、激光扫描等非接触式表面检测技术的发展为获取路面纹理形貌信息提供了多种便捷支持[7].其中激光扫描技术基于三角测量原理[8],可快速准确地采集路面的纹理形貌信息并生成点云模型,广泛应用于路面抗滑性能与路面养护技术的研究.

在进行纹理指标计算之前需要对纹理点云进行预处理以保证纹理指标的可靠性.国际标准化组织(ISO)提出了一套点云处理流程[9-11],主要包括:缺漏修正、波长过滤、倾斜与偏移抑制等步骤.其中,点云数据的倾斜与偏移多由路面自身坡度或扫描系统标定差异而产生,需要对点云进行坐标校正.点云零基准线(面)是点云坐标校正环节的重要元素,决定了点云中各数据点在垂直于水平面方向上的波动程度,Goubert等[12]也称其为计算辅助水平线.彭毅等[13]全面总结了区域三维纹理特征参数的计算公式、高度参数、体积参数和功能参数等常用指标的计算结果与点云零基准线(面)的关系,基于不同点云零基准线(面)计算的纹理指标将具有显著差异.因此有必要确定出适用于路面纹理指标有效计算的点云坐标校正方法.

现有研究大多使用LTS(laser texture scanner)等点状激光扫描仪采集二维点云数据[14].Hong等[15]、徐自生[16]采用最小二乘法校正单个断面点云坐标,以二维点云高程平均值为零基准线.这种方式弱化了点云模型对实际路面纹理的表征精细度,纹理指标计算易产生误差.任万艳[17]、刘梦梅[18]将高密度二维点云集拼接为三维区域点云,采用最小二乘法依次校正每个二维点云坐标,以断面纹理指标平均值作为区域纹理指标.通过拼接的方式获得三维点云将使零基准面由一系列互相独立的零基准线构成,而非一个完整的水平面,这会导致路面纹理变形,基于此类零基准面计算得到的区域纹理指标的有效性也有待验证.目前,Handyscan、FreeScan等线状激光扫描仪可直接获取三维点云,若提出适用于三维点云的坐标校正方法,则可避免拼接二维点云对区域纹理指标计算结果的影响.

针对上述问题,本文探究了传统点云坐标校正方法的不足,分别针对二维点云与三维点云提出了相应的坐标校正方法;对比了在不同点云坐标校正方法下路面纹理指标的计算结果差异,结合路面纹理形貌重构图像确定出的点云坐标校正新方法更适用于断面纹理指标与区域纹理指标计算,为数字化技术研究路面抗滑性能提供支持.

1 路面纹理点云坐标校正方法

1.1 二维点云坐标校正方法

二维点云坐标校正方法普遍用于抑制单个断面的倾斜与偏移[18-19],以消除路面自身坡度以及测试设备震动的影响[20].该方法拟合出一条表征断面点云分布情况的直线,即断面趋势线,其斜率反应断面点云的整体倾斜情况,截距代表断面点云的偏移程度.用原始二维点云高程坐标减去对应的断面趋势线高程坐标,使断面趋势线与零基准线重合,就完成了二维点云的倾斜与偏移校正(见图1).

(a) 原始断面纹理

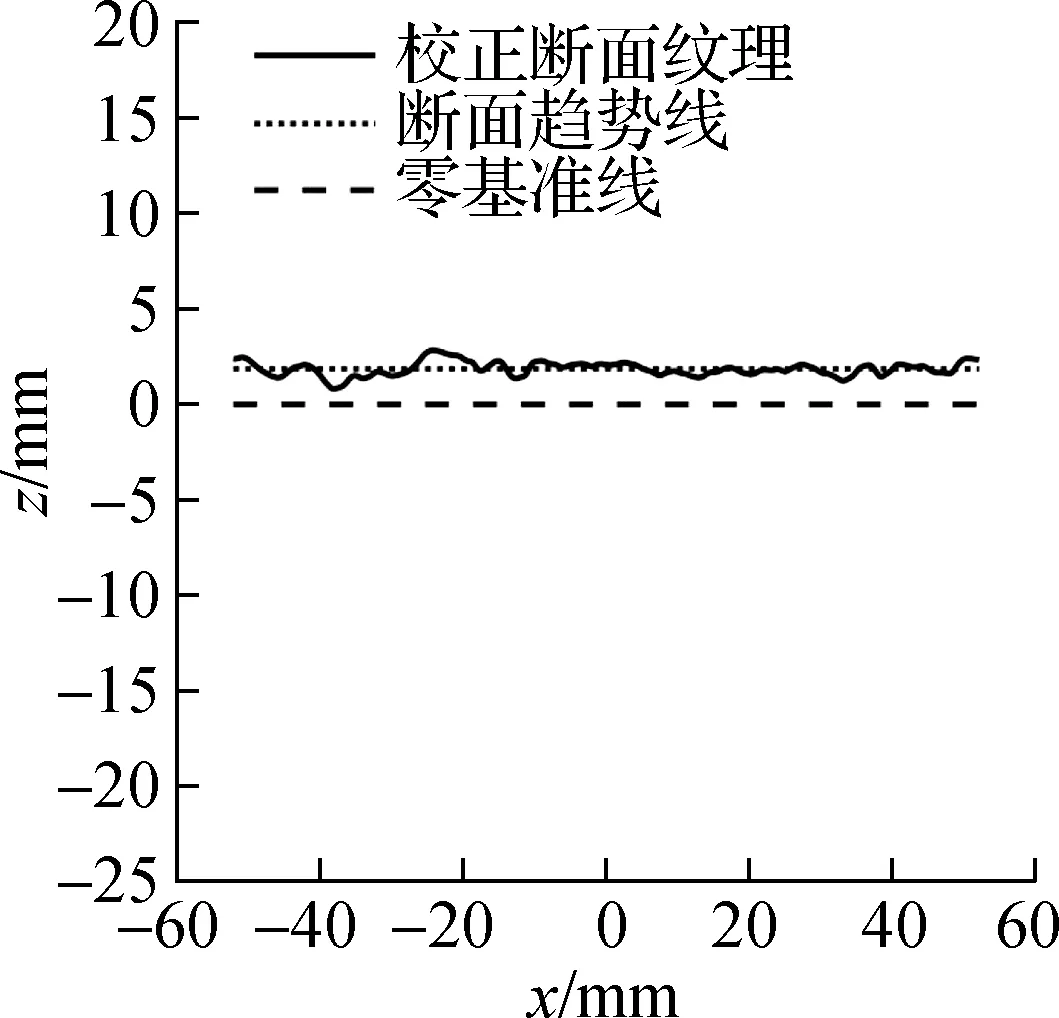
(b) 倾斜校正

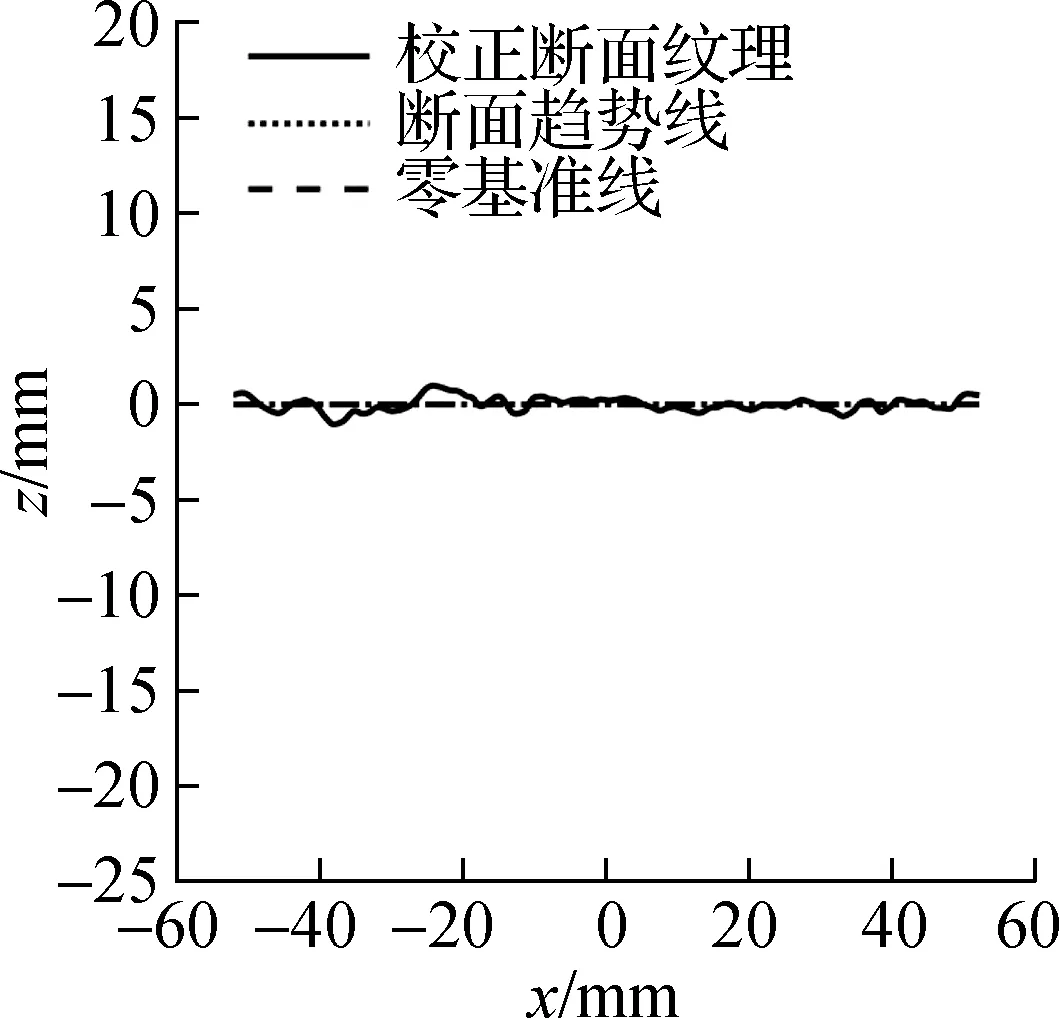
(c) 倾斜与偏移校正

1.1.1 传统二维点云坐标校正方法

标准ISO 13473-2∶2002[10]采用最小二乘法确定断面趋势线,提出了传统二维点云坐标校正方法,用公式表示为

(1)

(2)

Zi=zi-b1i-b0i=0,1,…,m-1

(3)

式中,i为二维点云数据点编号;zi、Zi分别为校正前后第i个二维点高程坐标;m为二维点云数据点总数;b1为断面趋势线斜率;b0为断面趋势线截距.

传统二维点云坐标校正方法沿坐标系纵轴(y方向)拟合点云,若沿坐标系横轴(x方向)则应用最小二乘法,将获得一条不同的断面趋势线,后者同样可作为点云校正的基准线使用,这就导致零基准线的不唯一性问题.简而言之,传统二维点云坐标校正方法在不同的拟合方向下将得到不同的零基准线,导致点云坐标校正结果不唯一.此外,文献[21]指出最小二乘法的误差会随拟合直线斜率绝对值的增大而增大,降低了传统二维点云坐标校正方法处理大坡度路段路面点云的准确性.

1.1.2 二维点云坐标校正新方法

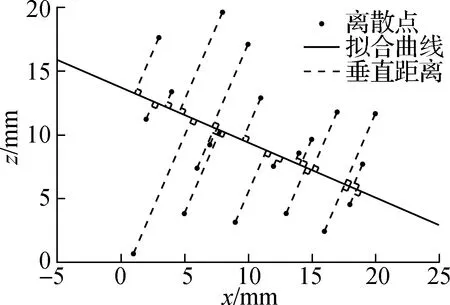
(a) 最小距离法

(b) 最小二乘法

最小距离法综合平面坐标系内2个坐标轴方向的偏差,通过求解欧氏距离的最小值进行拟合,相比最小二乘法更符合几何意义上的最佳拟合直线[23].因此,本文采用最小距离法确定断面趋势线,避免传统二维点云坐标校正方法产生零基准线不唯一性的问题,提出了二维点云坐标校正新方法.该方法相比于传统二维点云坐标校正方法,将式(1)更改为

(4)

式中

(5)

(6)

1.1.3 2种方法的稳定性对比

在路面纹理采集环节中,不同品牌型号的扫描设备通常具有不同的内置坐标系,同一扫描设备在各次作业中所建立的局部坐标系也会受到初始标定结果的影响,这将导致二维点云在不同坐标系下具有不同的断面趋势线,点云坐标校正结果将出现不稳定.为探究二维点云坐标校正方法的稳定性,本文以开级配抗滑磨耗层(OGFC)路面为例,采集图3(a)所示的二维点云片段,分别利用传统方法与新方法在不同坐标系内获取断面趋势线(见图3(b)和(c)).图中,坐标系x′oz′由坐标系xoz逆时针旋转角度θ得到.

如图3所示,坐标系x′oz′和坐标系xoz中的断面趋势线在新方法下完全重合,而在传统方法下存在偏离.这是由于点到直线的垂直距离在不同坐标系内是固定的,与坐标系方位无关(见图3(b));而点到直线的方差距离依赖于坐标系的纵轴方向(见图3(c)),坐标系x′oz′和坐标系xoz中的方差线分别平行oz′与纵轴oz.由此可以说明,相比传统二维点云坐标校正方法,新方法具有更好的稳定性,有助于评价来自不同扫描设备或在较大空间时间跨度下获取的路面纹理.

(a) 二维点云采集位

(b) 新方法拟合结果

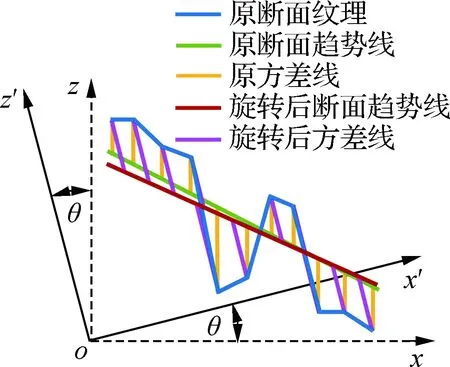
(c) 传统方法拟合结果图3 2种二维点云坐标校正方法的稳定性对比

1.2 三维点云坐标校正方法

二维纹理指标(仅由坐标(x,z)所确定)在表征具有三维属性(即包含区域坐标(x,y,z)信息)的路面纹理特征与摩擦学特性时具有一定局限性[24],同时考虑到轮胎与路面间的三维接触特性[4-5,25],有必要将路面纹理研究的基本单元从二维断面扩展到三维区域.

各种三维扫描设备的应用使获取路面纹理三维点云更加便捷[26-27],对三维点云同样也需要进行坐标校正.主要目标是消除:① 路面在横向与纵向上的坡度与用于指标计算的零基准面间的倾斜与偏移;② 不同扫描批次下扫描设备标定基准的差异,或不同扫描设备所建立内置坐标系的差异;③ 前期点云处理环节中使用逆向工程软件调整坐标系产生的人眼误差,或逆向工程软件捕捉不同点云模型零基准面间的差异.

1.2.1 传统三维点云坐标校正方法

目前三维路面纹理评价多采用基于断面纹理计算的二维评价指标的均值[28],对于整体考量区域纹理的纯三维指标的研究与应用较少.虽然目前已有大量三维扫描设备用于扫描路面纹理,但是传统三维点云坐标校正方法仍是一种基于二维点云坐标的切片面包式校正方法.该方法按照研究所需精度将三维点云拆分为一系列固定间距的二维断面点云集[19,26,29],然后独立地将各个二维点云的断面趋势线调至零刻度面.校正后的二维断面点云集经拼接即可得到校正后的三维点云.

本文沿平行二维断面方向(x方向)对断面趋势线进行投影,以探究传统三维点云坐标校正方法对断面趋势线的改变,并沿垂直二维断面方向(y方向)选取3个截面,进一步研究了三维纹理形貌的变化情况.断面趋势线投影面及截面见图4(a).

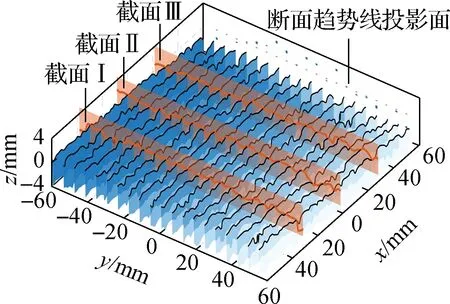
(a) 投影面及截面示意图

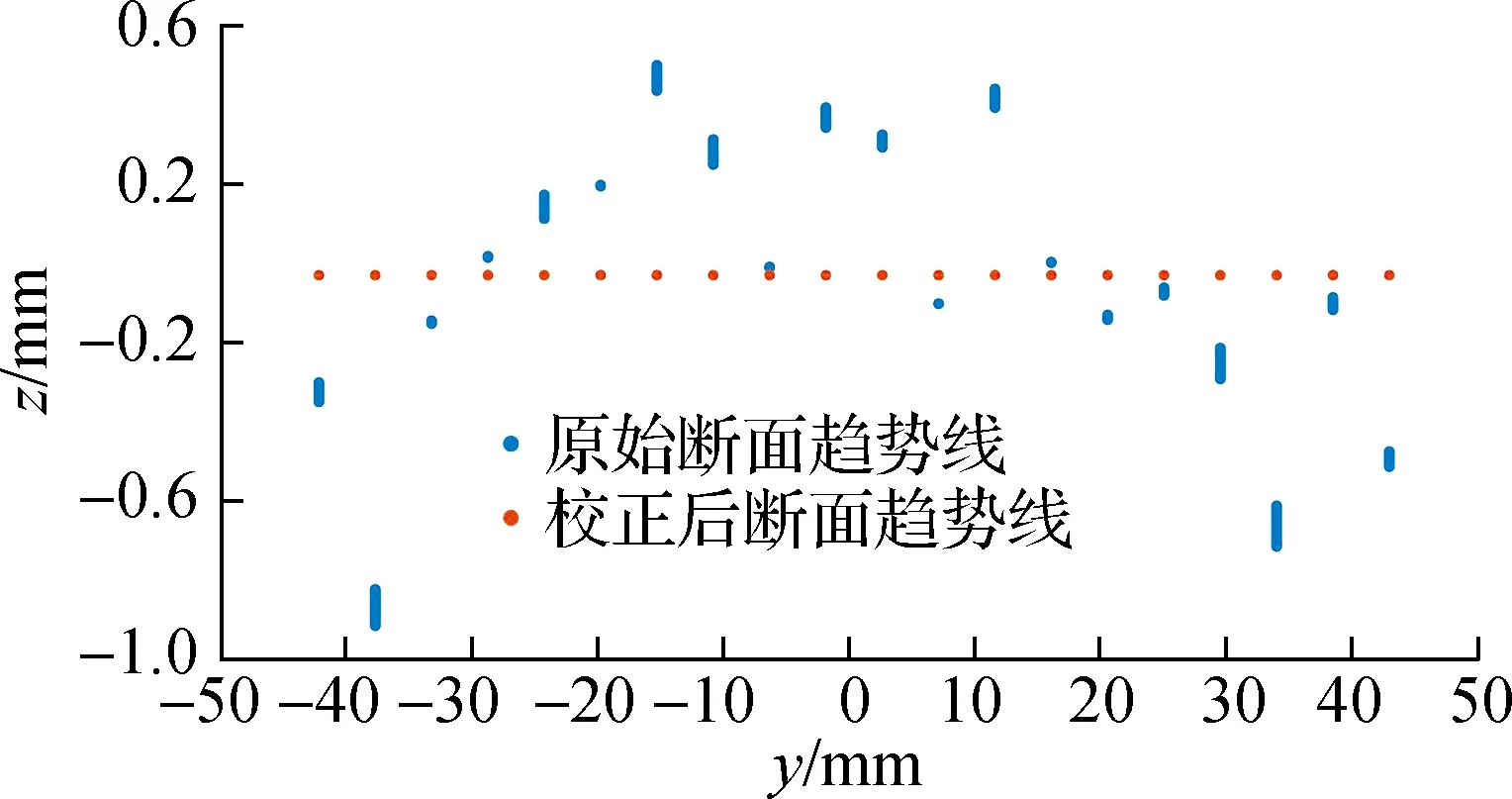
(b) 断面趋势线在投影面上的变化情况

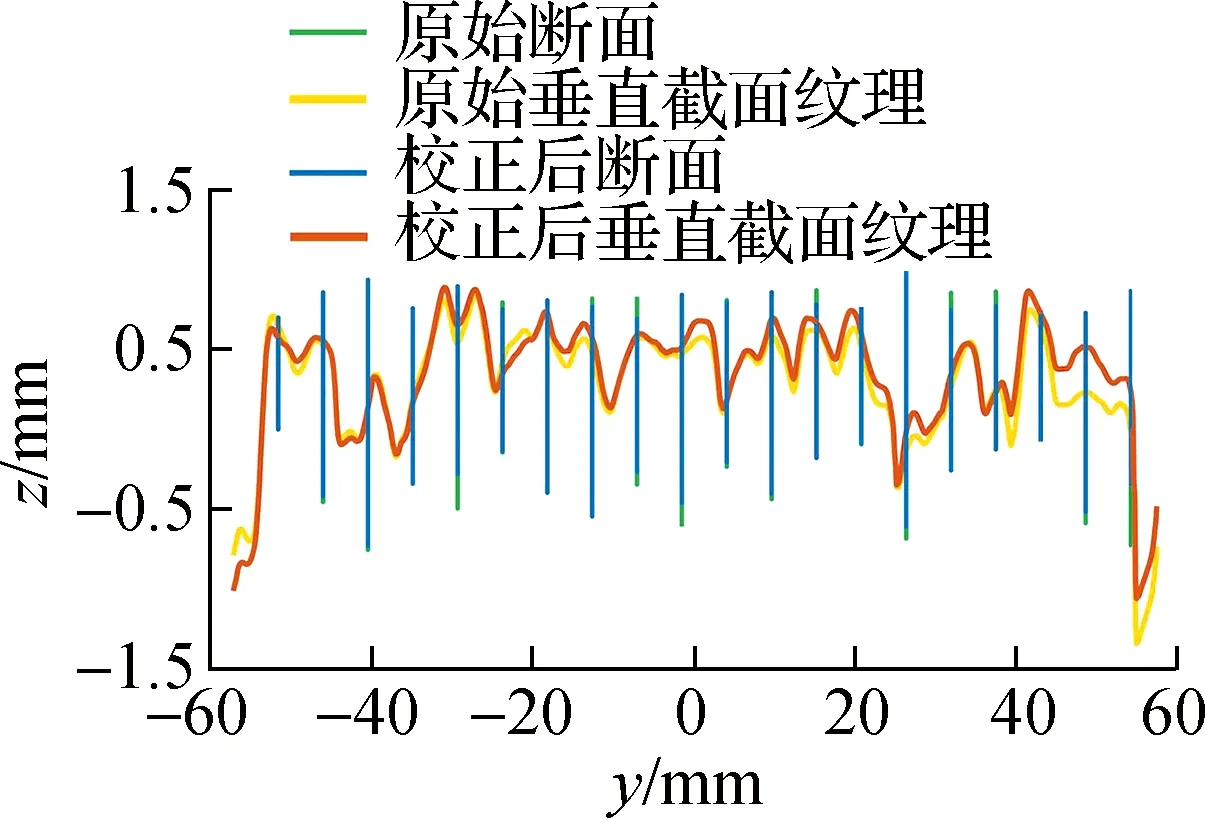
(c) 截面Ⅰ纹理变形

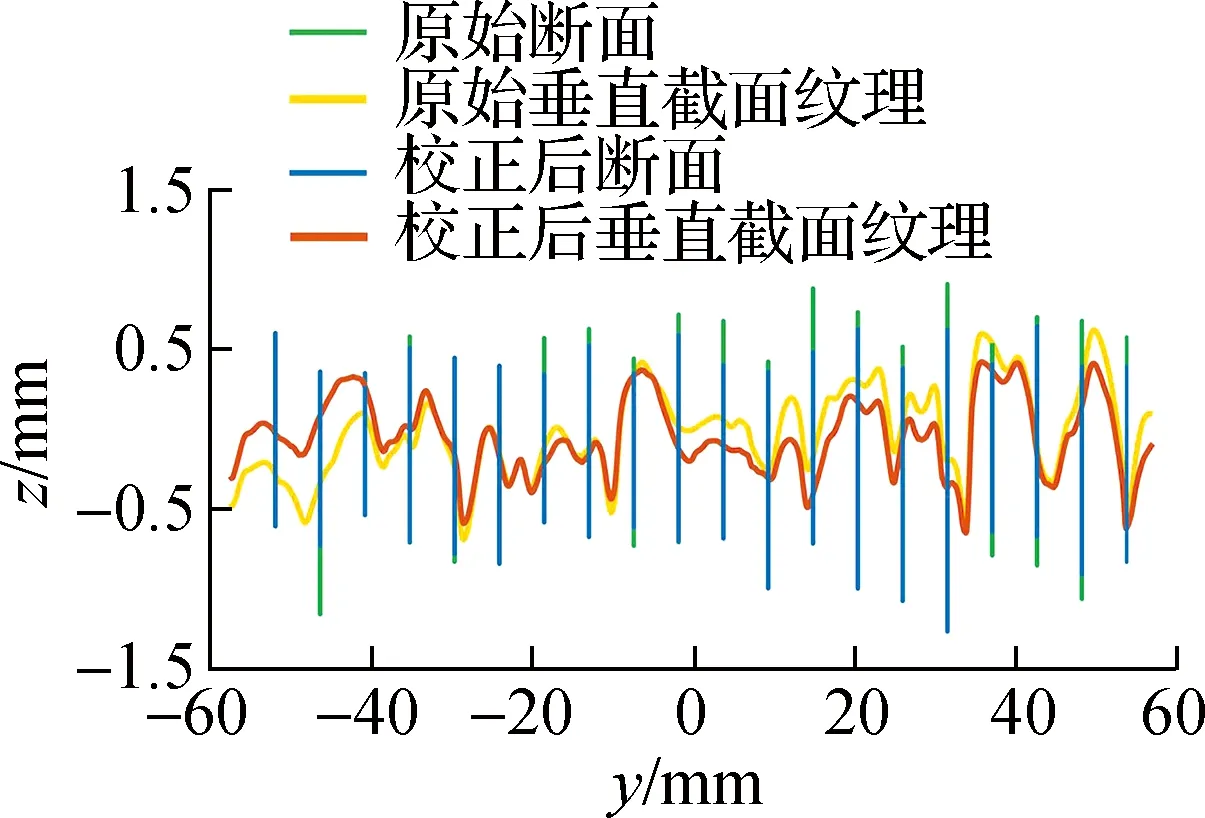
(d) 截面Ⅱ纹理变形

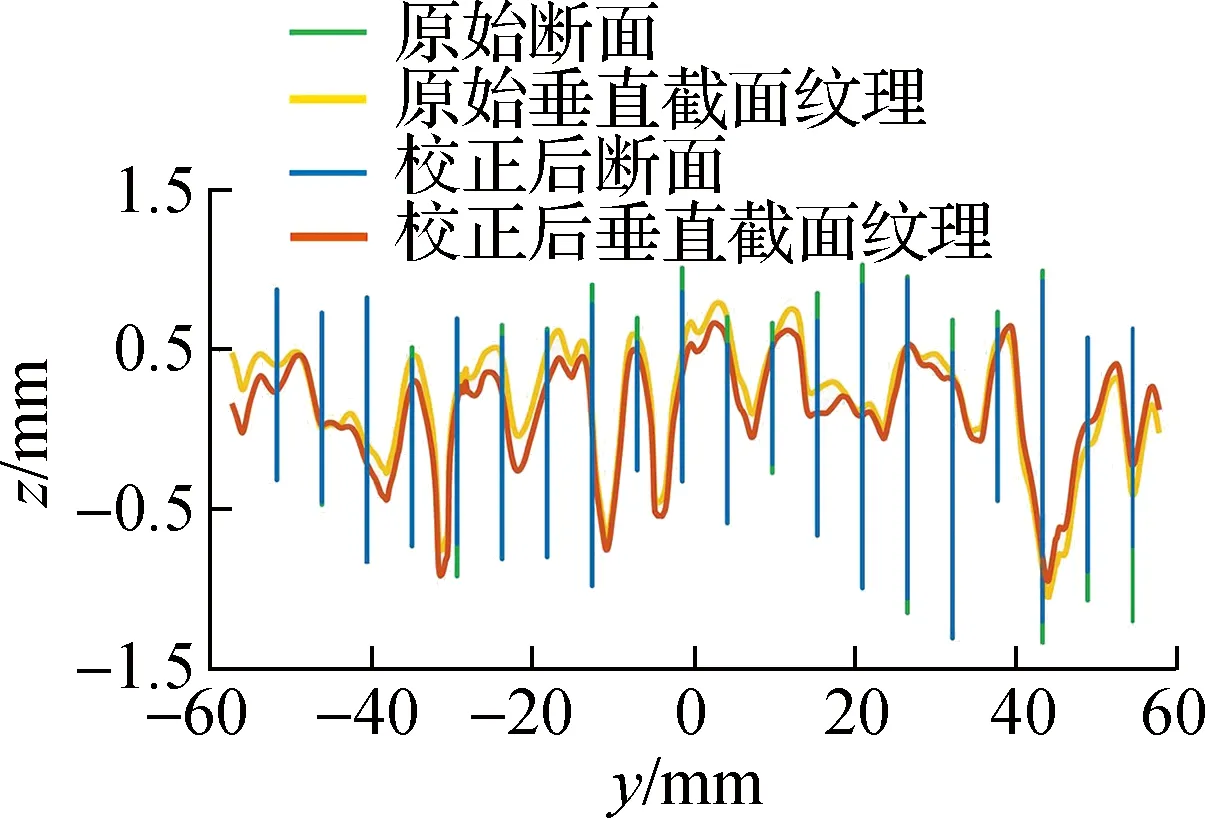
(e) 截面Ⅲ纹理变形

如图4(b)所示,在投影面上的原始断面趋势线具有不同的长度与高程,长度越长对应越大的倾斜程度.采用传统三维点云坐标校正方法后,各断面趋势线均为点状且位于零刻度线,说明各断面趋势线与零水平面重合.传统方法削弱了原本客观存在于各原始断面间的高度与角度差异,势必会导致三维纹理形貌的改变.

如图4(c)、(d)、(e)所示,本文任意选取了与拆分三维点云所得的二维断面相垂直的3个截面,其纹理形貌均在传统三维点云坐标校正方法下发生了不均匀变形,上凸纹理与下凹纹理的陡峭程度、高程变化量以及起讫位置等特征均被改变,纹理特征均趋于平滑.结合图4(b)可知,传统方法独立地校正每个断面趋势线至零刻度处,使各二维断面发生不协调的转角与位移.由此得出,传统三维点云坐标校正方法的不足在于因各断面间转角与位移的不协调而引起的三维纹理变形.

以一个典型的路面坑槽扫描实例来说明传统三维点云坐标校正方法所带来的纹理形貌失真问题.坑槽实际形貌见图5(a),坑槽最大深度约为5.7 cm.首先使用FreeScan UE Pro型手持激光三维扫描仪获取路面坑槽的原始三维点云(见图5(b)),扫描仪主要参数见表1.然后选定0.1 mm的拆分间距对其应用传统三维点云坐标校正方法,校正结果见图5(c).由图可知,原始三维点云具有明显的坑槽特征,而校正后的三维点云高程分布集中于零刻度面附近,坑槽特征消失,显著地改变了原始纹理形貌.虽然图5所示的坑槽扫描案例为路面纹理采集环节的一种特殊情况,但有效地说明了传统三维点云坐标校正方法的不足,即三维纹理的变形失真问题.

(a) 坑槽实际形貌

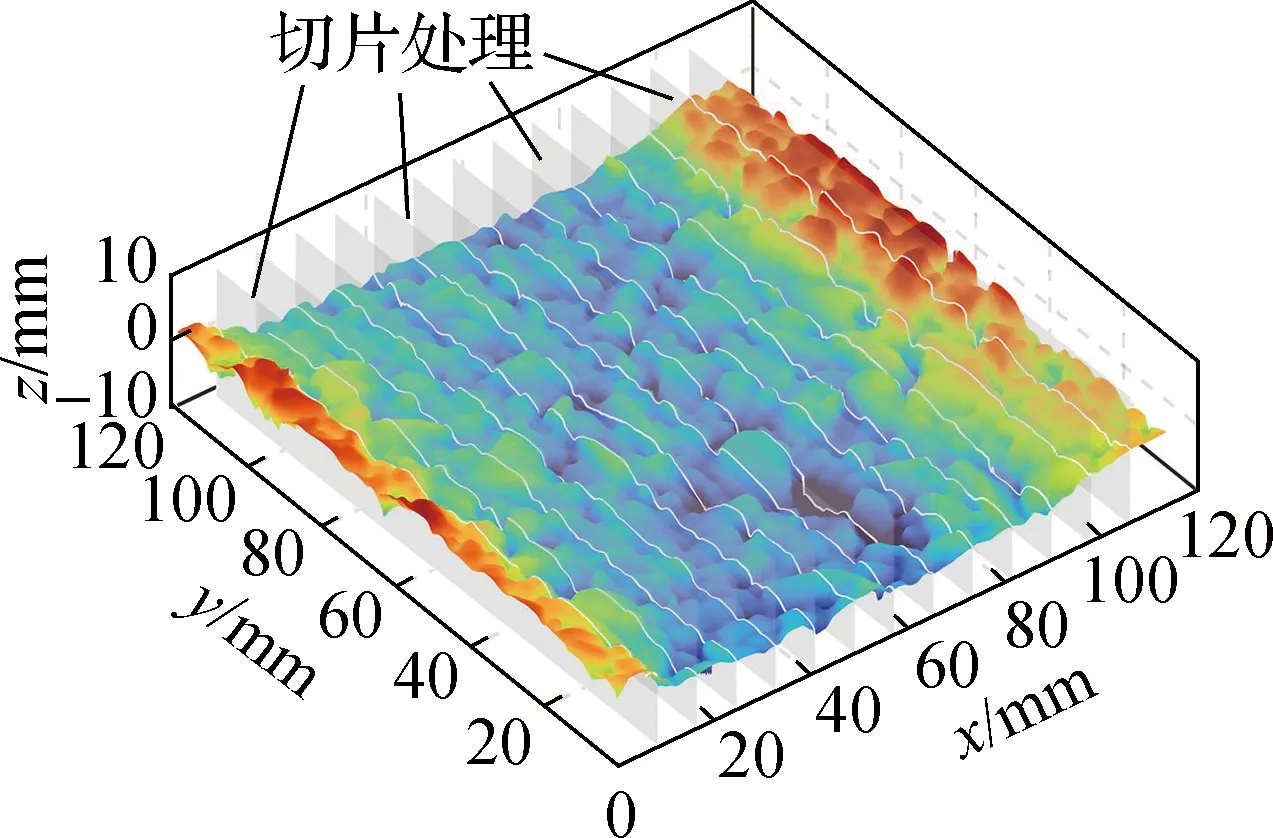
(b) 原始三维点云

(c) 传统方法校正后的三维点云

表1 FreeScan UE Pro型手持激光三维扫描仪主要参数

1.2.2 三维点云坐标校正新方法

要解决传统三维点云坐标校正方法的不足,应将三维点云视作一个整体进行校正,采用可唯一确定的平面来代替一系列将发生不协调转角与位移的断面趋势线,即点云趋势面,以点云趋势面作为三维点云坐标校正的基础,从而避免三维点云的变形,该过程见图6.

(a) 原始三维点云及其趋势面

(b) 校正后三维点云及其趋势面

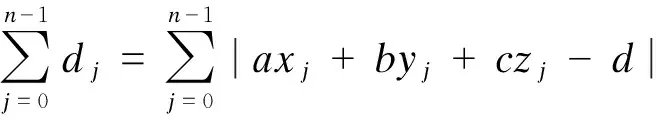
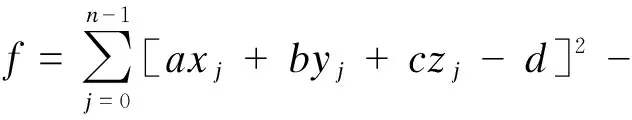
(7)

式中,实数λ为拉格朗日乘数;j为三维点云数据点编号;n为三维点云数据点总数.

特征值法沿x、y、z轴3个方向进行拟合,可以在不同坐标系下保持良好的稳定性.因此,本文采用特征值法确定点云趋势面,提出了三维点云坐标校正新方法,具体步骤如下:

① 将式(7)对d求偏导,令其偏导数为0,则有

(8)

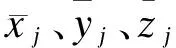
② 求解实对称矩阵A的最小特征值λmin与对应的特征向量{a,b,c},即

(9)

③ 将特征向量{a,b,c}代入式(8)求解参数d,确定点云趋势面方程ax+by+cz=d.

④最后,按下式进行三维点云坐标校正,即

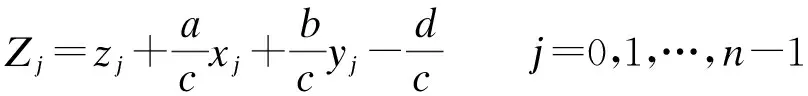
(10)

式中,zj、Zj分别为校正前后第j个三维点云高程坐标.

2 基于不同点云坐标校正方法的纹理指标计算结果分析

2.1 5种纹理指标

为比较点云坐标校正新方法与传统方法下纹理指标计算结果的差异,本文选取了公称最大粒径为13 mm的沥青混凝土(AC-13)、开级配抗滑磨耗层(OGFC-13)以及公称最大粒径为3 mm的环氧沥青面层(EAP-3)3种路面作为研究对象,使用FreeScan UE Pro型手持激光三维扫描仪获取二维与三维点云.参考常用指标[15,33-35]与标准ISO 13473-2∶2002[10]推荐指标,计算了5种纹理指标.

2.1.1 平均断面深度

平均断面深度(MPD)将二维断面点云分为等长的2段,取2段最高峰值的平均值与断面点云均值之差得到MPD,计算公式为

(11)

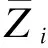
2.1.2 估计平均构造深度

估计平均构造深度(EMTD)依据铺砂法原理进行计算,二维点云基于图7(a)所示的点云峰顶线进行计算,三维点云基于图7(b)所示的点云峰顶面进行计算.二维点云的估计平均构造深度TEMTD-2D和三维点云的估计平均构造深度TEMTD-3D的计算公式分别为

(12)

(13)

式中,Zp(xi)为二维点云峰顶线方程;p、q为三维点云在x、y方向上数据点编号;s、t为三维点云在x、y方向上数据点总数;Zp(xp,yq)为三维点云峰顶面方程;Zpq为校正后x方向第p个、y方向第q个三维点云高程坐标.

图7(b)所示的峰顶面Zp(xp,yq)将显著影响TEMTD-3D的计算结果.本文参考Dan等[36]所提出的纹理参考平面概念,选定三维点云高程分布的4.8%分位数作为峰顶面Zp(xp,yq),计算TEMTD-3D.

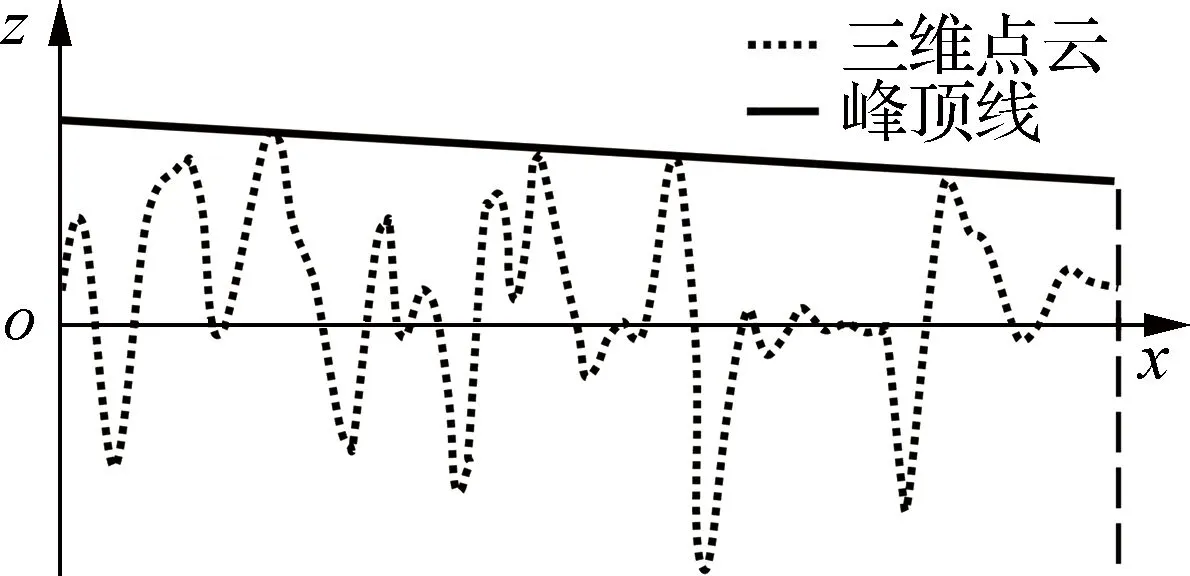
(a) 二维点云及其峰顶线

(b) 三维点云及其峰顶面图7 峰顶线与峰顶面示意图

2.1.3 纹理均方根偏差

纹理均方根偏差Rms为点云偏距的均方根值,二维点云的纹理均方根偏差Rms-2D和三维点云的纹理均方根偏差Rms-3D的计算公式分别为

(14)

(15)

2.1.4 纹理斜偏度

纹理斜偏度Rsk常用于衡量点云高程概率密度函数曲线分布的对称性.Rsk>0,则纹理凸峰尖锐凹峰平坦;Rsk<0,则纹理凸峰宽平凹峰狭窄;Rsk=0,则纹理凸峰凹峰形态相近.二维点云的纹理斜偏度Rsk-2D和三维点云的纹理斜偏度Rsk-3D的计算公式分别为

(16)

(17)

2.1.5 纹理陡峭度

纹理陡峭度Rku常用于衡量点云高程概率密度函数曲线峰部的尖度.Rku>3,则纹理高程分布陡峭;Rsk<3,则纹理高程分布平缓;Rsk=3,则纹理高程正态分布.二维点云的纹理陡峭度Rku-2D和三维点云的纹理陡峭度Rku-3D的计算公式分别为

(18)

(19)

2.2 二维点云坐标校正方法下的纹理指标对比

根据标准ISO 13473-1∶2019[9]要求,本文分别在AC-13、OGFC-13、EAP-3三种路面的轮迹带中心线上选取8个长度为1 m的断面,获取二维点云,分别应用二维点云坐标校正新方法与传统方法消除点云倾斜与偏移,计算每种路面在2种校正方法下的断面纹理指标.计算结果见表2.

表2 断面纹理指标计算结果

由表2可知,在2种二维点云坐标校正方法下,断面纹理指标计算结果并没有显著差异,各个纹理指标及其标准差十分接近,这说明在同一坐标系下由最小二乘法与最小距离法确定出的断面趋势线之间的差异是可以忽略的.但考虑到在不同坐标系下的校正方法的稳定性,二维点云坐标校正新方法更具优势.

另外,表2中所列的纹理指标均具有较大标准差.从指标类型来看,Rsk最为显著;从路面类型来看,OGFC-13最为显著.这表明所选取的8个断面间纹理差异性强,仅以单个断面的纹理指标表征路面纹理特征是不可靠的.因此,有必要获取三维点云以计算区域纹理指标.对于OGFC-13等纹理指标波动较大的路面,建议扩大扫描范围以获得稳定的指标计算结果.

2.3 三维点云坐标校正方法下的纹理指标对比

根据标准ISO 13473-1∶2019[9]要求,本文分别在AC-13、OGFC-13、EAP-3三种路面的轮迹带中心线上选取8个尺寸为120 mm×120 mm的矩形区域,获取三维点云.利用MATLAB软件分别应用三维点云坐标校正新方法与传统方法.其中,传统方法以0.1 mm的间距将三维区域点云拆分为二维断面点云集,依次沿横、纵方向应用二维点云坐标校正新方法.另外,本文根据《公路路基路面现场测试规程》(JTG 3450—2019)通过铺砂法获取了3种路面的实测构造深度(TD)作为参照.纹理指标计算结果见表3,纹理形貌对比见图8.

由表3可知,2种三维点云坐标校正方法下的纹理指标计算结果存在明显的差异,Rku最为显著.3种路面在新方法下EMTD与TD之间的偏差分别降为传统方法下的18.52%、47.79%与34.30%,表明三维点云坐标校正新方法对原始路面纹理特征的复原精度更好.

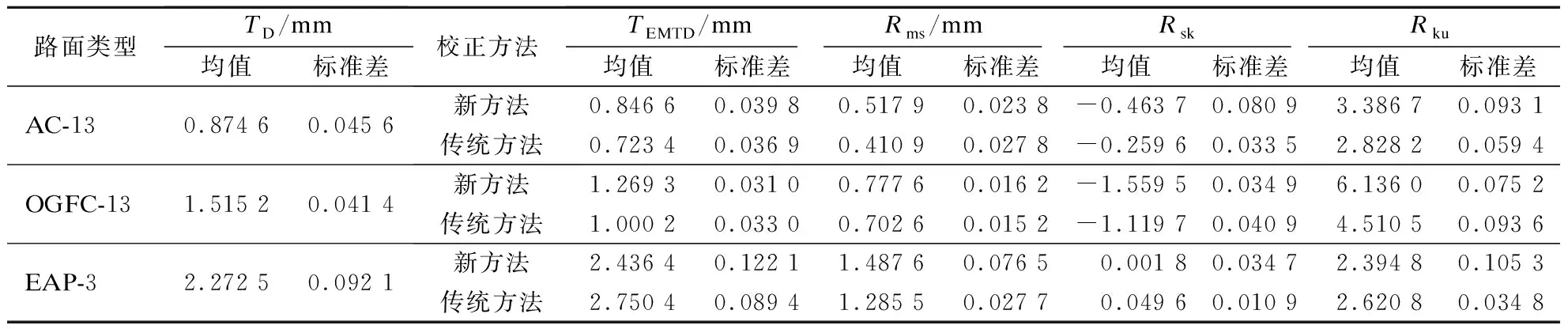
表3 区域纹理指标计算结果

传统三维点云坐标校正方法下的Rms更小,即点云偏离点云趋势面的程度更小,三维区域纹理趋于平滑,这是导致传统方法下EMTD与TD差异更大的重要因素.对应于图8中新方法下纹理形貌的色域更宽,即点云的高程分布范围更广,进一步验证了2种校正方法下Rms的差异.

2种校正方法下AC-13与OGFC-13路面的Rsk<0,EAP-3路面的Rsk>0,参考以正纹理(Rsk>0)与负纹理(Rsk<0)对路面的分类方法[37],判断AC-13与OGFC-13为负纹理路面,EAP-3为正纹理路面.正纹理路面在传统三维点云坐标校正方法下的纹理斜偏度绝对值|Rsk|更大,对应路面纹理中低于零基准面的下凹尖峰数量减少;负纹理路面在传统三维点云坐标校正方法下的纹理斜偏度绝对值|Rsk|更小,对应路面纹理中高于零基准面的上凸尖峰数量减少.图8也反映了这一变化规律,图8(h)所示的纹理形貌相较于图8(i)深蓝色区域的面积减少,而图8(b)与(e)所示的纹理形貌相较于图8(c)与(f)亮黄色区域面积减少.

(a) AC-13实际纹理形貌

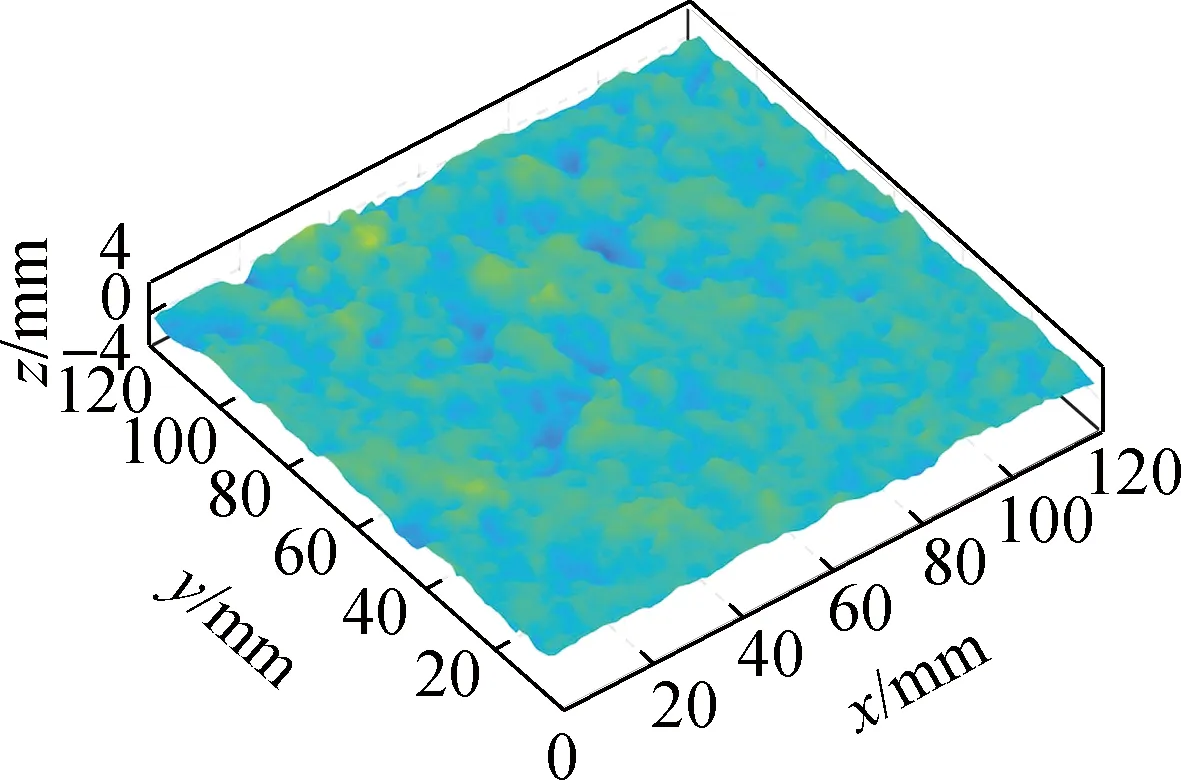
(b) 应用传统方法校正的AC-13

(c) 应用新方法校正的AC-13

(d) OGFC-13实际纹理形貌

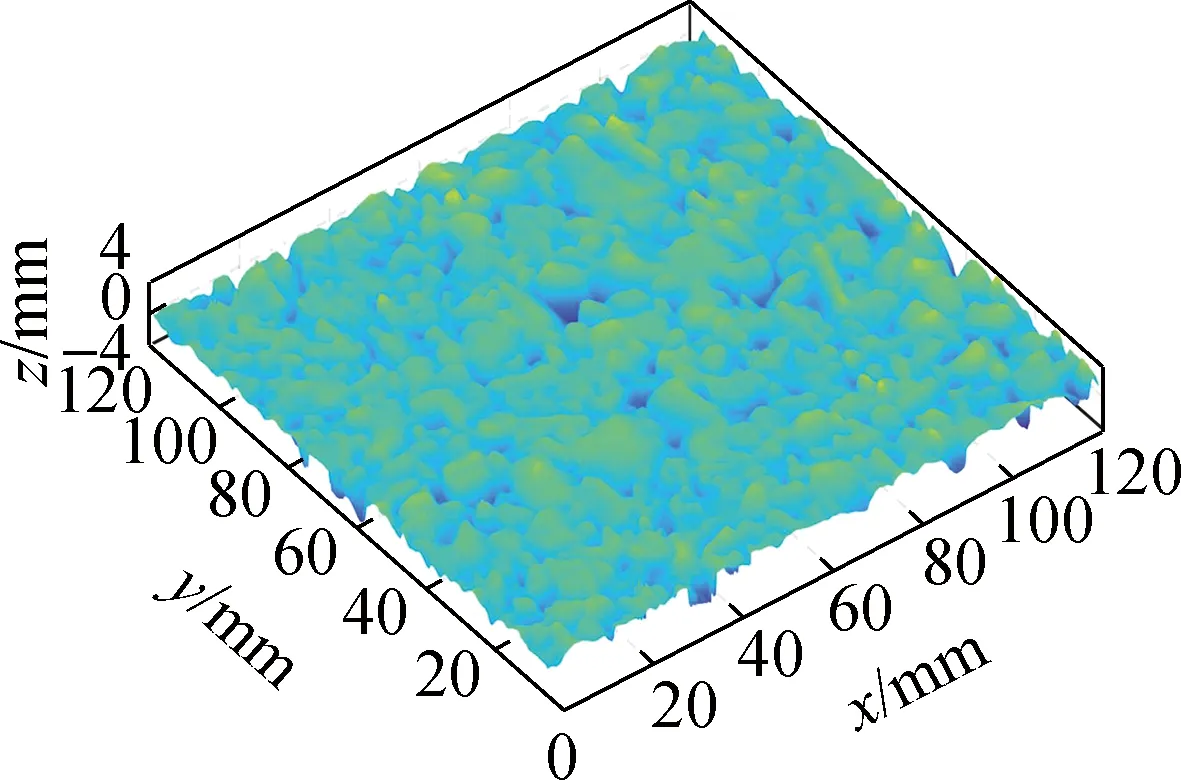
(e) 应用传统方法校正的OGFC-13

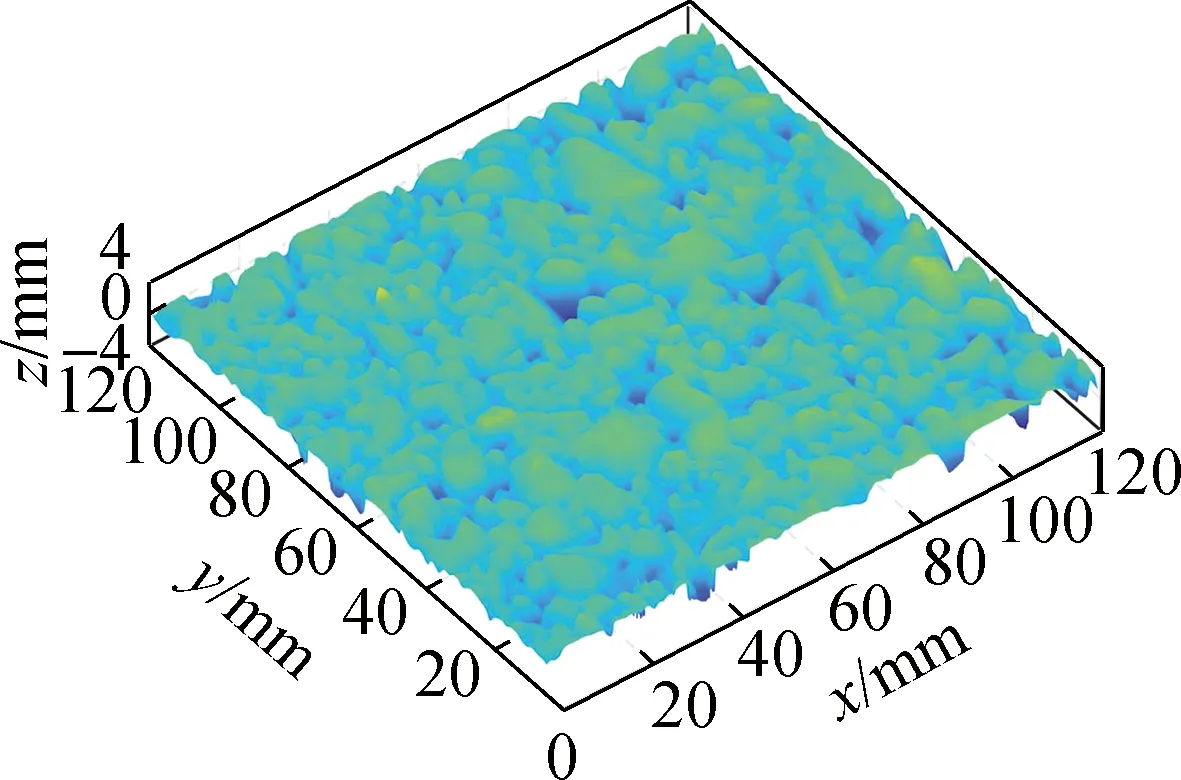
(f) 应用新方法校正的OGFC-13

(g) EAP-3实际纹理形貌

(h) 应用传统方法校正的EAP-3

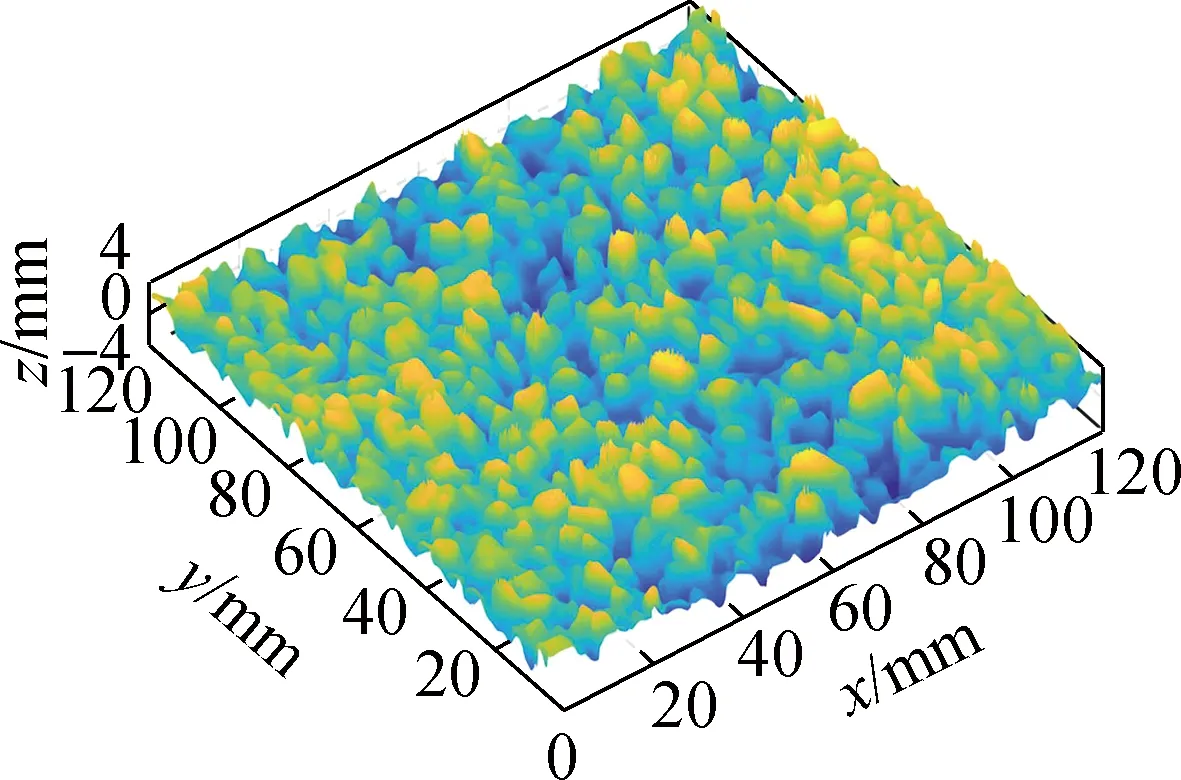
(i) 应用新方法校正的EAP-3

AC-13与OGFC-13两种负纹理路面在传统三维点云坐标校正方法下的Rku更小,即高于零基准面的低频度极端值数量减少,对应于图8(b)与(e)中纹理形貌向亮黄色区域的过渡相较于图8(c)与(f)更加平缓;而正纹理路面EAP-3在传统三维点云坐标校正方法下的纹理陡峭度Rku更大,即低于零基准面的低频度极端值数量减少,对应于图8(h)中纹理形貌向深蓝色区域的过渡更加平缓.

综合以上分析,传统三维点云坐标校正方法改变了路面纹理的形貌特征,使路面纹理趋于平滑,并且纹理指标计算结果与实测值偏差较为显著.三维点云坐标校正新方法更适用于三维区域纹理指标计算,提高了路面纹理形貌的复原精度与路面纹理指标计算结果的有效性.

3 结论

1) 基于最小距离法提出了二维点云坐标校正新方法,该方法的校正结果不受初始坐标系的限制,具有良好的稳定性,解决了基于最小二乘法的传统校正方法的结果随扫描设备型号或设备标定误差而改变的问题.

2) 传统三维点云坐标校正方法降低了纹理均方根偏差Rms,区域纹理趋于平滑:对于正纹理路面,增大了纹理斜偏度绝对值|Rsk|与纹理陡峭度Rku,减少了区域纹理中低于零基准面的下凹尖峰数量与低频度极端值;对于负纹理路面,降低了纹理斜偏度绝对值|Rsk|与纹理陡峭度Rku,减少了区域纹理中高于零基准面的上凸尖峰数量与低频度极端值.

3) 基于特征值法提出了三维点云坐标校正新方法,将区域点云视作一个整体进行坐标校正,避免了传统校正方法产生区域纹理的变形,更真实地还原了路面的纹理形貌.在新方法下,对于研究选用的3种路面样本(OGFC-13、AC-13、EAP-3),纹理均方根偏差Rms大于传统方法,更贴近实际路面纹理状态.EMTD与TD的偏差减小为传统方法的47.79%以下,新的方法提高了路面纹理形貌的数字化重构精度,更适用于区域纹理指标的计算.

4) 本文提出的二维与三维点云坐标校正新方法有助于提高路面纹理形貌的重构精度与路面纹理指标的计算准确度,为利用激光扫描等非接触式纹理测量方法评估路面工程的抗滑性能或噪声特性提供了一种优化方法,具有一定的应用前景.