基于气弹试验 15 MW 超长柔性叶片颤振临界风速预测的叶根反力法
陆曼曼 柯世堂 吴鸿鑫 高沐恩 田文鑫 王浩

摘要: 颤振是风力机叶片超大化发展必须解决的首要难题,气弹模型测振风洞试验是其最有效的预测方法之一,但传统方法无法精确解决模型相似比和测量精度的难题。本文提出一种基于主梁刚度等效原则的超长柔性叶片气动/刚度映射一体化三维完全气弹模型设计方法,采用高速摄像技术和高频六分量天平进行全风向角同步测振和测力风洞试验;系统研究了 NREL?15 MW 超长柔性叶片的非线性动态响应频谱特性,对比分析了基于叶尖位移与叶根反力的风力机叶片颤振性能和临界失稳状态,发现了采用叶根反力来预测颤振性能的可行性,提出了超长柔性叶片颤振失稳预测的叶根反力法。研究表明:本文提出的气弹模型设计和实验方法能精确有效地模拟风力机叶片动力性能与颤振行为,试验发现超长柔性叶片在桨距角为 93°~96°和 284°~287°区间内发生颤振,颤振区间内颤振临界风速随桨距角的增大呈现先减小后增大的趋势,在桨距角为 94°时达到最小,其风洞临界风速为 5.4 m/s;叶根反力与叶尖位移存在一致发散性和强相关性,提出的叶根反力颤振指标 δ≥2% 时,风力机叶片进入颤振临界状态。
关键词: 15 MW 超长柔性叶片;气弹模型设计方法;同步测振测力试验;颤振临界风速;叶根反力法
中图分类号: TK83 文献标志码: A 文章编号: 1004-4523(2023)03-0718-11
DOI:10.16385/j.cnki.issn.1004-4523.2023.03.014
引 言
随着风电机组朝着超大功率发展,风力机叶片愈发朝着超长、柔、细演变,由此带来的结构和气动双重非线性[1?3]导致的风力机叶片振动,尤其是失稳性颤振必须得到解决。在强风等恶劣天气条件下,大型风力机叶片颤振风毁事故[4?8]屡见不鲜,如 2003年台风“杜鹃”及 2006年台风“桑美”导致的风力机叶片扭转颤振破坏。传统的风力机叶片颤振预测方法(多参数法[9]、变形激盘法[10]和特征值法[11]等)对于大型风力机叶片这种在流场中存在众多非线性、非定常因素以及承受复杂负荷的结构很难做到准确预测。因此,建立超长柔性叶片颤振临界风速准确、有效的预测方法,具有重要的理论和应用价值。
目前针对风力机叶片颤振预测的研究多采用数值模拟方法[12?14],其颤振预测分析方法主要有频域分析和时域分析。频域分析[15?17]方法以 Hansen[18?19]提出的基于多叶片坐标变换[20?21]计算方法最为典型,通过坐标变换改进算法求解特征值来求解风力机叶片颤振临界转速,但其简化了气动模型并忽略了流体与结构耦合,很难精准预测颤振临界状态。时域分析[22?24]方法的基本思路是,通过希尔伯特?黄变换[25?26]提取逐增风轮转速叶尖幅值突增的扭转或弯曲模态对应的时程及其包络线,判断风力机叶片是否发生颤振,但其只考虑风力机叶片一阶模态,忽略了高阶模态的影响。气弹模型风洞试验[27?30]是研究颤振性能的最有效手段之一,但由于风力机叶片翼型不规则,其截面、刚度、质心等沿展长不规则分布使得其氣弹模型设计难;又因缩尺模型尺寸小但变形大,其测点布置及捕捉难、干扰性强且测量精度低,导致国内外缺少超长柔性叶片三维颤振气弹模型试验研究。现有研究仅采用二维翼型测压、测力试验[31?34],其验证了二维翼型测压测力的一致性,为后期振荡翼型的风洞试验研究提供了新方法,但二维翼型无法完整反映三维超长柔性叶片的气弹失稳性能。
鉴于此,本文以 NREL?15 MW 超长柔性风力机叶片为研究对象,考虑风力机叶片复合材料和结构的双重非线性,提出了基于主梁刚度等效原则的超长柔性叶片三维完全气弹模型设计方法,并采用高速摄像技术和高频六分量天平进行全风向角同步测振和测力风洞试验,对比分析了基于叶尖位移与叶根反力的风力机叶片颤振性能和临界失稳状态,发现了采用叶根反力来预测颤振性能的可行性,最后提出了超长柔性叶片颤振失稳预测的叶根反力法。
1 超长柔性叶片气弹模型
1. 1 叶片参数
本文以美国可再生能源实验室 NREL?15 MW风力机的配套超长柔性叶片作为气弹模型风洞试验的 研 究 对 象 ,其 风 轮 直 径 为 240 m,轮 毂 高 度 为150 m,叶片全长为 117 m,叶尖预弯为 4 m,质量为65.252 t,最大弦长为 5.77 m,叶根直径为 5.2 m,叶片质心位于 26.8 m 处,叶片采用的翼型为 FFA?W3系列。风力机叶片几何参数详见表 1。
1. 2 气弹试验模型设计
结构动力学相似和气动外形相似是气弹模型设计的基本原则[35]。叶片气弹模型风洞试验需要模拟几何尺寸、风场特性和气动弹性特性。气弹相似条件物理量可采用无量纲参数来表示 ,如 Reynolds数、Froude 数、Cauchy 数、密度比、阻尼比等,而风力机叶片所在流场空气为低速、不可压缩、牛顿黏性流体,其流体运动方程与结构运动方程为:
对流体运动方程所有项乘以 λl/λ 2u,对结构运动方程考虑减缩频率相同,即 λbλω/λV=1。为保证原型和模型流体运动与结构运动的相似性,物理量的比值需满足:
考虑风洞阻塞率要求 ,模型几何缩尺比选为λl=1/70,其他无量纲参数在风力机叶片气弹模型风洞试验中也需严格模拟,具体相似参数见表 2。由于风力机叶片气弹模型的柔性大、弹性范围要求高,等效主梁材料弃用传统机翼气弹模型常用的金属材料,采用弹性区间大且轻质的聚酰胺纤维材料。风力机叶片因其各向异性铺层复合材料制作工艺带来的沿展长刚度分布不规则问题,使缩尺模型各截面几何形状需独立设计。为了准确模拟真实风力机叶片的刚度沿展长的变化规律,并同时实现缩尺模型水平弯曲刚度、垂直弯曲刚度和扭转刚度的分别对应,等效刚度梁截面形状采用异形变截面十字形。根据模型控制截面的目标刚度设计其具体尺寸,在刚度变化明显的地方增加控制截面数量,在刚度区别不大的地方减少控制截面数量,共计10个主梁控制截面。控制截面采用二次线性内插,保证主梁光滑过渡,使得梁段尺寸由叶根到叶尖逐渐减小。由于风力机缩尺模型叶尖尺寸极小,等效刚度梁截面在满足尺寸要求时不足以提供其相对刚度,故在风力机叶片相对展长80%的位置不再设置等效刚度梁截面,刚度由加强肋提供。因高频六分量天平作为风力机叶片的支撑件,其刚度对模型的频率有一定的影响,本文所采用的原型风力机叶片叶根刚度为46.5 MPa,根据相似准则,风力机叶片气弹模型质量轻且叶根具有足够刚度,从而降低了高频六分量天平刚度对模型频率的影响。风力机叶片气弹模型结构理论刚度与实际刚度对比及等效刚度梁截面形状见图1。
气弹模型采用“主梁+维形框段”的结构形式,为了保证模型的气动外形以及维形框段不提供附加刚度,框段采用和主梁单点联结整体打印的三维框架。聚酰胺纤维主梁(变截面异形梁)提供全部刚度,维形框段采用聚酰胺纤维 3D打印,为防止风力机叶片变形时框段接触而产生附加刚度,相邻框段间有 3 mm 间隙,外部采用轻质木片填充节段模型的前缘、后缘与檩条之间的空隙,保证模型的气动外形。通过质量块调整配重使模拟模型的重心和转动惯量满足设计要求。三维风力机叶片气弹模型结构设计及制作见图2。
2 风洞试验方法与结果分析
2. 1 工况设置与测量系统
试验风洞为回流式风洞,试验段长为 20.0 m,宽为 2.5 m,高为 2.0 m,最大风速为 50.0 m/s。风力机叶片气弹风洞试验在均匀流场中进行,来流风方向以垂直叶片预弯方向定义为 0°桨距角,顺时针为正角度方向,在风洞试验中通过逆时针转动试验模型来实现,共 36 个桨距角,每个桨距角测量 7 个风速工况,逐级加载。最终风洞试验中风力机叶片气弹模型布置如图 3 所示。本试验采取的测量方案是振动?反力同步测量以建立其同步相关性,整个气弹试验测量系统分为高速摄像观测系统、高频六分量天平振动实时采集系统和风洞实时风速测量系统。
高速摄像观测系统共分为两部分:顶部高速摄像系统(观测叶尖挥舞位移与摆振位移)布置在风洞内顶部,由信号延长线外接控制室信号分析系统;外部水平高速摄像系统(观测风力机叶片竖向沉浮)。高频六分量天平底端与风洞转盘固接,顶端与风力机叶片气弹模型连接,通过采集系统实时测量根部六分力。风洞试验段参考高度处布置眼镜蛇进行实时风速采集 。风洞试验高速摄像采样频率为330 Hz,采样时间为 5 min;叶根高频六分量天平采样频率为 1000 Hz,采样时间为 5 min。
为验证气弹试验模型风力机叶片与真实风力机叶片的运动相似性,采用锤击法测出真实模型的固有频率,通过测量试验模型的固有振动特性进行风力机叶片气弹模型标定。表 3 为气弹模型风力机叶片与真实风力机叶片的结构动力特性对比分析。发现真实风力机叶片与数值气弹模型和风洞气弹模型的各阶模态固有频率基本吻合,前四阶模态误差均在 10% 以内,表明气弹模型的动力学特性与真实风力机叶片匹配较好,保证了气弹模型的颤振特性与真实风力机叶片的相似精度。
2. 2 颤振区间确定
图 4给出了风速分别为 7.1 m/s和 8.7 m/s时(实际风速分别为 59.4 m/s和 72.8 m/s)风力机叶片不同桨距角下叶尖挥舞、摆振位移均方根变化曲线。由图 4 可知,当风速一定时,风力机叶片在桨距角 93°~96°及 284°~287°区间时,叶尖位移均方根突增,在两个区间内其挥舞位移均方根最大值分别出现在桨距角为 94°和 286°时;其他桨距角叶尖位移均方根在 0~0.2 cm 幅值内波动,无明顯变化,故初步判定桨距角93°~96°及 284°~287°区间内发生颤振。
取风洞风速为 7.1 m/s(实际风速为 59.4 m/s)时叶尖位移均方根最大值对应的桨距角进行分析。图5 为桨距角为 286°时叶尖位移振动幅值时程曲线及不同阶段位移功率谱。可发现风力机叶片发生颤振过程中,其叶尖位移随时间的增加共经历三个阶段:第 1 阶段为短时蓄振阶段,风力机叶片积累能量,表现为无规则抖振;当风力机叶片积累一定能量后进入第 2 阶段,即发展阶段,叶尖位移随时间增加而增大,进入发散阶段;第 3阶段为稳定阶段,当叶尖位移发散后进入一定值附近,其表现为简谐振动的“软颤振”[36]。风力机叶片在颤振三阶段中,其功率谱主导频率幅值随阶段演变逐渐变大,而主导频率随阶段演变逐渐变小,最终在稳定阶段达到最小,其主导频率逐渐趋近于结构固有频率 4.68 Hz。对比分析可发现,挥舞位移振幅明显大于摆振位移振幅,表明风力机叶片颤振失稳主要在挥舞方向。
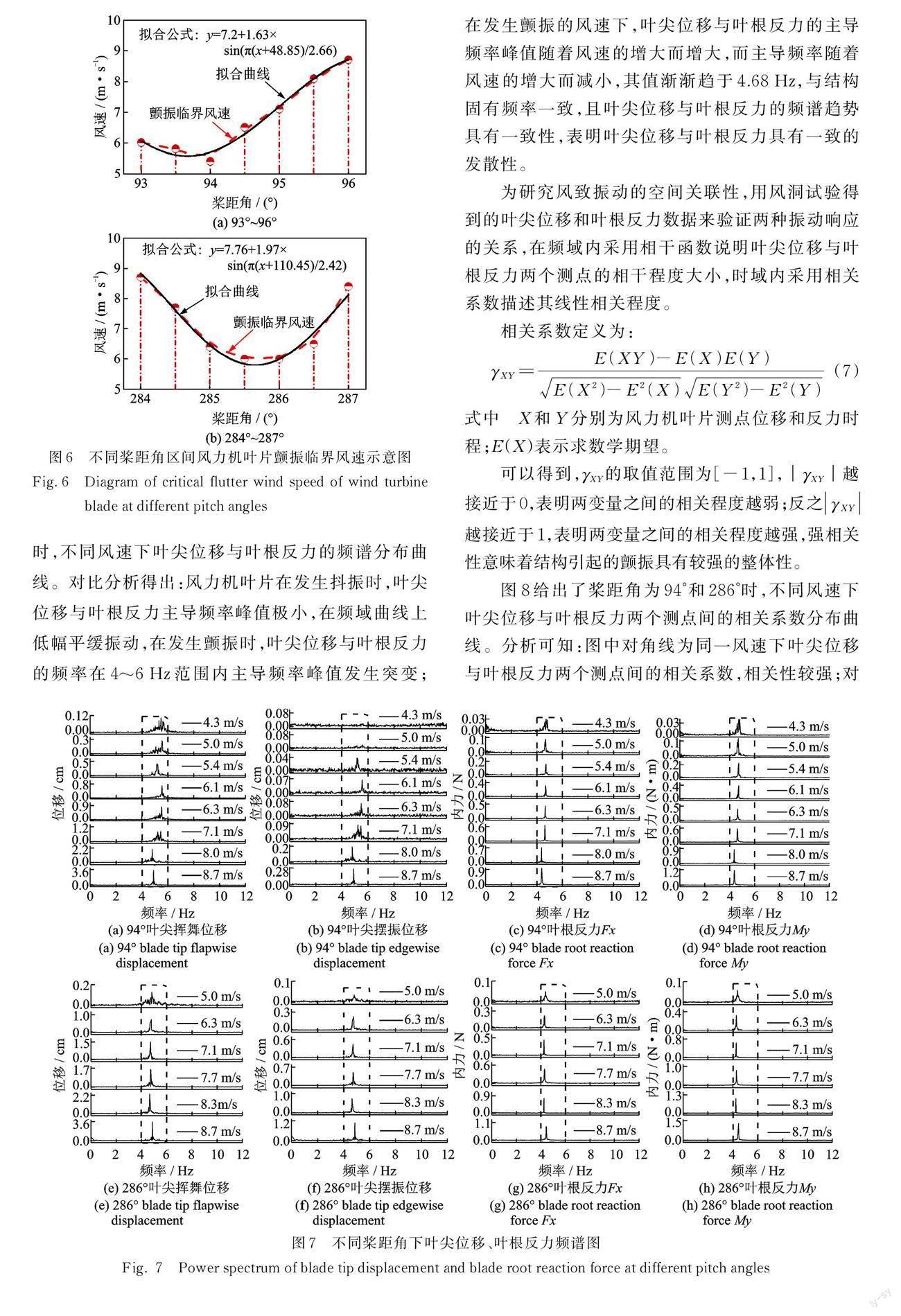
图 6 给出了由叶尖位移得出的颤振临界风速示意图。由图 6 可知:在颤振区间内,临界风速随桨距角的增大呈先减小后增大的趋势,在桨距角为 94°和286°时达到最小,其风洞临界风速分别为 5.4 m/s 和6.0 m/s(实际临界风速分别为 45.2 m/s和 50.2 m/s)。颤振临界风速与拟合曲线吻合较好,因风力机叶片翼型的不对称,颤振区间以 190°呈现反对称分布。
3 颤振预测叶根反力法
3. 1 反力?位移一致发散分析
图 7 给出了风力机叶片在桨距角为 94°和 286°时,不同风速下叶尖位移与叶根反力的频谱分布曲线。对比分析得出:风力机叶片在发生抖振时,叶尖位移与叶根反力主导频率峰值极小,在频域曲线上低幅平缓振动,在发生颤振时,叶尖位移与叶根反力的频率在 4~6 Hz 范围内主导频率峰值发生突变;在发生颤振的风速下,叶尖位移与叶根反力的主导频率峰值随着风速的增大而增大,而主导频率随着风速的增大而减小,其值渐渐趋于 4.68 Hz,与结构固有频率一致,且叶尖位移与叶根反力的频谱趋势具有一致性,表明叶尖位移与叶根反力具有一致的发散性。
为研究风致振动的空间关联性,用风洞试验得到的叶尖位移和叶根反力数据来验证两种振动响应的关系,在频域内采用相干函数说明叶尖位移与叶根反力两个测点的相干程度大小,时域内采用相关系数描述其线性相关程度。
相关系数定义为:式中 X 和 Y 分别为风力机叶片测点位移和反力时程;E(X)表示求数学期望。
可以得到,γXY的取值范围为[?1,1],│γXY│越接近于 0,表明两变量之间的相关程度越弱;反之 | | γXY越接近于 1,表明两变量之间的相关程度越强,强相关性意味着结构引起的颤振具有较强的整体性。
图 8 给出了桨距角为 94°和 286°时,不同风速下叶尖位移与叶根反力两个测点间的相关系数分布曲线。分析可知:图中对角线为同一风速下叶尖位移与叶根反力两个测点间的相关系数,相关性较强;对角线两侧是两测点之间不同风速下叶尖位移与叶根反力的相关系数,离对角线距离越远表示两个测点风速差别越大,相关系数也随着风速差值的增大而减小。相较于抖振,风力机叶片发生颤振时,叶尖位移与叶根反力两个测点间的相关系数大,相关性强。综上可得,当风力机叶片发生颤振时,叶尖位移与叶根反力存在较强的相关性。
相干函数是在频域范围内对结构进行动力分析计算的关键参数,反映了风荷载在频域内的空间相干性,是影响风致响应的主要因素之一,定义为:式中 Pxx ( f ) 和 Pyy ( f ) 分别为信号 x(t)和 y(t)的自谱密度函数;Pxy(f)为两个信号的互谱密度函数。根据风洞试验获得叶尖位移与叶根反力时程曲线,分析不同风速和不同桨距角下叶尖位移与叶根反力的相干特性。
图 9 给出了桨距角为 94°和 286°时,不同风速下叶尖位移与叶根反力两个测点间的相干函数分布曲线。对比分析可知:叶尖位移与叶根反力相干函数分布曲线呈先平缓后减小再平缓波动的趋势;在发生抖振的风速,叶尖位移与叶根反力相干函数在频率为 3 Hz 时开始骤减,随后趋于 0;在发生颤振的风速,叶尖位移与叶根反力相干函数在频率为 4.7 Hz时开始骤减,随后趋于 0,其骤减频率与结构固有频率相一致。叶尖位移与叶根反力低频区相干函数显著大于高频区相干函数,低频区相干函数趋于 1,高频区相干函数趋于 0。故当风力机叶片发生颤振时,低频区叶尖位移与叶根反力存在较强的相干性。
3. 2 颤振判定准则
颤振判定准则是判断结构是否发生气弹失稳的重要指标,本文基于叶根反力与叶尖位移的一致发散性,选取超长柔性风力机叶片的叶根二分量反力(Fx 和 My)为目标时程变量,以叶根反力颤振判定准则来判断叶片是否发生颤振,定义超长柔性风力机叶片颤振临界状态设计表达式:γ ? δ ≥[ δ ] (9)式中 γ 为结构重要性系数,取为 1.1;δ 为结构颤振反力指标;[δ]为结构颤振反力容许值。
定义超长柔性风力机叶片的叶根反力颤振指标δ 为 3 s 时距叶根二分量反力(Fx 和 My)的相对标准差斜率极值,其表达式为:式中 κ ( a )t = 3 s 为超长柔性风力机叶片 3 s 时距内叶根反力(Fx 和 My)的相对标准差;f 为叶根二分量反力采样频率(本文 f=1000 Hz);a 与 aˉ 分别为叶根反力 3 s 时距内反力样本和样本均值;n 为 3 s 时距内反力样本的个数;E ( a ) 为 3 s 时距内反力样本的采样数学期望值。因为目标时间太短数据不稳定,目标时间太长无代表性,综合考虑实验数据的稳定性,t选取为 3 s。式 中 Δ( a ) 为 3 s 时 距 内 叶 根 二 分 量 反 力(Fx 和My)的相对标准差的斜率,其值要求大于等于 0,若小于 0,则表示不会发生颤振。
δ = max ( Δ( a )Fx,Δ( a )My ) (12)式中 δ 为结构颤振反力指标,即 3 s 时距内叶根二分量反力(Fx 和 My)的相对标准差的斜率的最大值对应的叶根二分量反力颤振指标,当指标值大于一定值时所对应的风速为风力机叶片颤振临界风速。
图 10 给 出 了 不 同 风 速 下 颤 振 工 况(桨 距 角93°~96°,284°~286°)与抖振工况(桨距角 0°~360°)的超长柔性风力机叶片 δ?v 曲线。由图 10 分析可知:所有桨距角下叶根反力颤振指标 δ 均随着风速的增大逐渐变大;对于颤振工况(桨距角 93°~96°,284°~286°),叶根反力颤振指标 δ 在颤振临界风速处存在突增的现象,δ 随风速变化呈现非线性关系;而对于抖振工况(桨距角 0°~360°),δ 随着风速的增加 近 似 为 线 性 关 系 。 当 桨 距 角 区 间 为 93°~96°和284°~286°时,风洞风速分别低于 5.4 m/s 和 6.0 m/s(实际风速分别为 45.2 m/s 和 50.2 m/s)时,该区间内桨距角下的叶根反力颤振指标 δ 均小于 2%。考虑一定安全系数下,定义风洞风速为 6.0 m/s 作用下叶根反力颤振指标容许值[δ]=2.2%。结合 δ?v 曲线中发散容许值,强风作用下超长柔性风力机叶片颤振临界风速状态可表示为:
图 11 给出了由叶尖位移得出的颤振临界风速与由叶根反力法得出的颤振临界风速的对比图。由图 11 可知,两种判定方法得到的临界风速在颤振区间内趋势基本一致。表明以叶根反力法判定颤振临界风速的可靠性。
3. 3 有效性验证
为评估本文提出的基于叶根二分量反力的叶根反 力 颤 振 判 定 法 的 有 效 性 ,基 于 OpenFAST 构 建NERL?15 MW 风力机数值计算模型,通过约束塔架变形、风轮转动、偏航系统和变桨系统,逐级改变风向与风速,获取其数值模拟颤振风速与桨距角。以风力机叶片振动位移时程判断风力机叶片的颤振临界风速,图 12 给出了基于 OpenFAST 在颤振桨距角为 94°时,不同风速下叶尖挥舞位移时程对比示意图。对比分析表明:风速为 55 m/s 时,基于 Open?FAST 求得的叶尖位移呈发散趋势,且其发散阶段为三段式分布,与本文全风向气弹风洞试验结果趨势一致。通过数值模拟和未预弯气弹风洞试验求得的叶尖挥舞位移与叶根反力数据,表 4 给出了叶根反力法与传统叶尖位移法判断风力机叶片颤振临界风速的对比列表。对比分析表明,叶根反力法和传统叶尖位移法的风力机叶片颤振判定预测结果吻合较好。
4 结 论
本文系统研究了 15 MW 风力机超长柔性叶片颤振形态、发生机理及判别准则,提出了风力机叶片气弹模型设计方法、风洞试验测量方法和基于叶根反力的颤振预测方法。具体研究结论如下:
(1)提出一种基于主梁刚度等效原则的超长柔性风力机叶片气动/刚度映射一体化三维完全气弹模型设计方法:风力机叶片相对展长 0~80% 位置由异形变截面十字梁提供风力机叶片等效刚度,后段风力机叶片刚度由加强肋提供;风洞气弹模型总体结构形式采用“主梁+维形框段”整体 3D 打印。采用高速摄像技术和高频六分量天平进行全风向角同步测振和测力风洞试验。风洞试验验证了本文提出的气弹模型设计和试验方法能精确有效地模拟风力机叶片的动力性能与颤振行为。
(2)葉片风致振动分为三个阶段:第 1 阶段为短时蓄振阶段,风力机叶片积累能量,表现为无规则抖振;当风力机叶片积累一定能量后进入第 2 阶段,即发展阶段,叶尖位移随时间增加而增大,进入发散阶段;第 3 阶段为长时间稳定阶段,当叶尖位移发散后进入一定值附近后,其表现为简谐振动的“软颤振”。
(3)风力机叶片在桨距角 93°~96°和 284°~287°区间内发生颤振,颤振区间内颤振临界风速随桨距角的增大呈现先减小后增大的趋势,在桨距角为 94°和 286°时颤振临界风速最小,风洞临界风速分别为5.4 m/s 和 6.0 m/s(实际临界风速分别为 45.2 m/s和 50.2 m/s),因风力机叶片翼型的不对称,颤振桨距角区间呈 190°反对称分布。
(4)叶根反力与叶尖位移存在较强的一致发散性和强相关性,提出了基于叶根反力的超长柔性风力机叶片颤振性能指标。当叶根反力颤振指标大于2% 时,风力机叶片发生颤振。
参考文献:
[1] 唐迪,陆志良,郭同庆 . 大型风力机整机气动弹性响应计算[J]. 振动工程学报,2015,28(1):38?43.TANG Di, LU Zhiliang, GUO Tongqing. Aeroelastic simulations of a large horizontal?axis wind turbine[J].Journal of Vibration Engineering,2015,28(1):38?43.
[2] MCKENNA R, OSTMAN P, FICHTNER W. Key challenges and prospects for large wind turbines[J]. Re?newable and Sustainable Energy Reviews,2016,53:1212?1221.
[3] WANG Lin, LIU Xiongwei, KOLIOS A. State of the art in the aeroelasticity of wind turbine blades: aeroelas?tic modelling[J]. Renewable and Sustainable Energy Reviews,2016,64:195?210.
[4] 王力雨,许移庆 . 台风对风电场破坏及台风特性初探[J]. 风能,2012,27(5):74?79.
Wang Liyu, Xu Yiqing. Preliminary study on the dam?age of typhoon to wind farm and typhoon characteristics[J]. Wind Energy,2012,27(5):74?79.
[5] Chen X, Xu J Z. Structural failure analysis of wind tur?bines impacted by super typhoon Usagi[J]. Engineering Failure Analysis,2016,60:391?404.
[6] 陈斌,王凯,刘健,等 . 0608 号台风“桑美”过境前后对长 江 口 外 海 域 环 境 的 影 响[J]. 地 球 科 学 ,2016,41(8):1402?1412.
CHEN Bin, WANG Kai, LIU Jian, et al. The impact of super typhoon Saomai (0608) on the offshore envi?ronment near the Yangtze estuary[J]. Earth Science,2016,41(8):1402?1412.
[7] Ishihara T, Yamaguchi A, Takahara K, et al. An analy?sis of damaged wind turbines by typhoon Maemi in 2003[C]. Proceedings of the Sixth Asia?Pacific Conference on Wind Engineering, Seoul, Korea. 2005:1413?1428.
[8] Kikitsu H, Okuda Y, Okada H. High wind damage in Japan from typhoon Maemi and Choi?wan on September 2003[C]. Agenda 36th Joint Meeting Panel On Wind and Seismic Effects, Tsukuba, Japan. 2004.
[9] 周盛 . 叶轮机气动弹性力学引论[M]. 北京:国防工业出版社,1989:202?231.
Zhou Sheng. Introduction to Aeroelasticity of Turboma?chinery[M]. Beijing: National Defense Industry Press,1989:202?231.
[10] Adamczyk J J, Stevens W, Jutras R. Supersonic stall flut?ter of high?speed fans[J]. ASME: Journal of Engineering for Gas Turbines and Power,1982,104(3):675?682.
[11] Bendiksen O O, Friedmann P P. The effect of bending?torsion coupling on fan and compressor blade flutter[J]. ASME: Journal of Engineering for Gas Tur?bines and Power,1982,104(3):617?623.
[12] 任勇生,张明辉 . 水平轴风力机叶片的弯扭耦合气弹稳定性研究[J]. 振动与冲击,2010,29(7):196?200.
Ren Yongsheng, Zhang Minghui. Aeroelastic stability of a horizontal axis wind turbine blade with bending?torsion coupled[J]. Journal of Vibration and Shock,2010,29(7):196?200.
[13] Ke S T, Yu W L, Wang T G, et al. Aerodynamic per?formance and wind?induced effect of large?scale wind turbine system under yaw and wind?rain combination ac?tion[J]. Renewable Energy,2019,136:235?253.
[14] 伍波,王骑,廖海黎,等 . 不同风攻角下薄平板断面颤振机理研究[J]. 振动工程学报,2020,33(4):667?678.
WU Bo, WANG Qi, LIAO Haili, et al. Flutter mecha?nism of thin flat plates under different attack angles[J].Journal of Vibration Engineering,2020,33(4):667?678.
[15] Vatne S R. Aeroelastic instability and flutter for a 10MW wind turbine[D]. Trondheim: Norwegian Univer?sity of Science and Technology,2011.
[16] LOBITZ D W. Aeroelastic stability predictions for a MW?sized blade[J]. Wind Energy,2004,7(3):211?224.
[17] Malcolm D J. Modal response of 3?bladed wind turbines[J]. Journal of Solar Energy Engineering,2002,124(4):372?377.
[18] Hansen M H. Aeroelastic stability analysis of wind tur?bines using an eigenvalue approach[J]. Wind Energy,2004,7(2):133?143.
[19] Hansen M H. Aeroelastic instability problems for wind turbines[J]. Wind Energy,2007,10(6):551?577.
[20] Johnson W. Helicopter Theory[M]. London, UK: Do?ver Publications,1994.
[21] Bir G. Multi?blade coordinate transformation and its ap?plication to wind turbine analysis[C]. Proceedings of 46th AIAA Aerospace Sciences Meeting and Exhibit,Reno,Nevada.2008.
[22] Chen B, Hua X G, Zhang Z L, et al. Monitoring of wind turbine blades for flutter instability[J]. Structural Monitoring and Maintenance,2017,4(2):115?131.
[23] Pirrung G R, Madsen H A, Kim T. The influence of trailed vorticity on flutter speed estimations[J]. Journal of Physics: Conference Series,2014,524:1?11.
[24] Lobitz D W. Parameter sensitivities affecting the flutter speed of a MW?sized blade[J]. ASME: Journal of So?lar Energy Engineering,2005,127(4):538?543.
[25] Huang N E, Shen S S P. Hilbert Huang Transform and Its Applications[M]. 2nd ed. Singapore: World Scien?tific Publishing Company,2014.
[26] Huang N E, Wu Z H. A review on Hilbert?Huang trans?form: method and its applications to geophysical studies[J]. Reviews of Geophysics,2008,46(2):2007RG000228.
[27] 宋兆泓,孔瑞蓮,魏星禄 . 风机叶片的防颤设计与试验分析[J]. 航空动力学报,1987,2(4):328?331.
Song Zhaohong, Kong Ruilian, Wei Xinglu. Experi?mental analysis and modification of a windmill fan for preventing flutter[J]. Journal of Aerospace Power,1987,2(4):328?331.
[28] 程鹏 . 水平轴风力机叶片气动弹性的风洞试验研究[D]. 哈尔滨:哈尔滨工业大学,2009.
Cheng Peng. Experimental study of aeroelasticity forthe blades of horizontal axis wind turbines[D]. Harbin:Harbin Institute of Technology,2009.
[29] Dimitriadis G, Li J. Bifurcation behavior of airfoil under?going stall flutter oscillations in low?speed wind tunnel[J]. AIAA Journal,2009,47(11):2577?2596.
[30] Razak N A, Andrianne T, Dimitriadis G. Flutter and stall flutter of a rectangular wing in a wind tunnel[J].AIAA Journal,2011,49(10):2258?2271.
[31] 汤瑞源,赵明亮,吴永健 . 测力法在翼型动态失速试验研究中的应用[J]. 气动实验与测量控制,1995,9(2):16?20.
Tang Ruiyuan, Zhao Mingliang, Wu Yongjian. The ap?plication of the force measurement method on experi?mental study of airfoil dynamic stall[J]. Journal of Ex?periments in Fluid Mechanics,1995,9(2):16?20.
[32] Jiao Yuqin, Zhang Binqian, Jin Chengxin, et al. Experi?mental technique on direct measuring of aerodynamics forces of airfoil[J]. Journal of Experiments in Fluid Me?chanics,2005,19(2):40?44.
[33] 焦予秦,陈希平,王龙,等 . 风力机翼型极大迎角风洞直接测力试验技术[J]. 太阳能学报,2014,35(10):1911?1916.
Jiao Yuqin, Chen Xiping, Wang Long, et al. Direct force measuring testing technique for wind turbine airfoil at very high attack angle in wind tunnel[J]. Acta Energi?ae Solaris Sinica,2014,35(10):1911?1916.
[34] 孫皓 . 风力机翼型失速颤振的实验与数值模拟研究[D]. 武汉:华中科技大学,2019.
Sun Hao. Experimental investigation and numerical sim?ulation on stall flutter of an oscillating wind turbine air?foil[D]. Wuhan: Huazhong University of Science and Technology,2019.
[35] Suatean B, Gletuse S, Colidiuc A. Aeroelastic prob?lems of wind turbine blades[J]. AIP Coference Proceed?ings,2010,1281(1):1867?1870.
[36] 朱乐东,高广中 . 典型桥梁断面软颤振现象及影响因素[J]. 同济大学学报(自然科学版),2015,43(9):1289?1294.
Zhu Ledong, Gao Guangzhong. Influential factors of soft flutter phenomenon for typical bridge deck sections[J]. Journal of Tongji University (Natural Science),2015,43(9):1289?1294.

