一种极值搜索的齿轮系统振动信号阶次跟踪方法

徐磊 丁康 何国林 王远航

摘要： 在变速工况下，齿轮系统的振动信号具有非平稳性，频谱特征模糊，不利于特征提取和故障诊断。阶次跟踪方法作为一种非平稳信号分析方法，将原信号从时间域转换到角度域，有助于抑制变转速导致的频率模糊现象。广泛应用的计算阶次跟踪分析方法在实现等角度重采样过程中，通过提取瞬时转速积分求取瞬时角位移，或者基于相位解调获取角度‐时间关系，受限于积分累计误差或小的转速跟踪范围。利用齿轮系统啮合振动信号峰峰值对应的等角度间隔特征，提出一种基于时域信号极值搜索的无键相阶次跟踪方法。所提方法不需要通过转速积分获取瞬时角位移，同时允许较大转速变化范围，降低了阶次分析域变换过程的误差，抗噪性能良好，使阶次谱能量集中度和特征成分辨识度得到明显提高。理论分析、仿真对比分析和试验测试结果均验证了所提方法的有效性，适用于变转速工况下的齿轮箱非平稳振动信号频谱分析和故障诊断。

关键词： 故障诊断；阶次跟踪；齿轮系统；极值搜索；角度‐时间关系

中图分类号： TH165+.3；TN911.7 文献标志码： A 文章编号： 1004-4523（2023）03-0837-08

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.026

引 言

齿轮系统通常运行在不同程度的变转速或者转速波动工况下，对应的振动响应信号为非平稳信号［1‐2］。由于转速的变化，齿轮振动信号在时域不再具有周期性，同时响应信号产生调频特征，频率泄漏和频谱模糊现象严重［3］。阶次跟踪方法作为一种有效的非平稳信号分析方法，将等时间间隔采样的非平稳信号转化为等角度间隔采样的准平稳信号，有效降低变转速或转速波动对频谱特征的影响。对原始信号进行等角度间隔采样，关键在于获得转角与时间的对应关系。可以在信号采集时通过转速信号或键相信号间隔等角度触发采样获得，该类方法称為硬件阶次跟踪（Hard Order Tracking， HOT）；也可基于时间‐角位移函数对时域采样信号进行等角度重采样重构得到，该类方法称为计算阶次跟踪（Computed Order Tracking， COT）。 此外，还有Vold‐Kalman阶次跟踪技术［4‐6］和基于Gabor变换的阶次跟踪分析［7‐8］。

由于不需要复杂的电路和额外的硬件设备，计算阶次跟踪已经成为工业领域应用最广泛的阶次跟踪方法［9］。在装有转速传感器或者编码盘的情况下，可对采集的瞬时转速进行时间积分获取时间‐角位移函数。Fyfe等［10］基于转速计信号，通过二次多项式插值建立角度‐时间关系，比较了不同的多项式插值方法对后续重采样过程的影响，得出结论：三次样条插值在构造相角‐时间函数以及重采样原始信号方面能获得最好的结果。然而，键相装置在某些场合安装困难，因此，无键相的阶次跟踪方法（Ta‐cholessOrderTracking，TLOT）成为国内外学者研究的重点。一种思路是基于转速的数值积分获取角度‐时间关系。转速可以通过时频分析方法获得［11‐13］。其中最重要的是从时频图中精确地提取出时频脊线。但是，旋转部件的瞬时相位信息才是阶次跟踪的必要输入量。由瞬时频率获得的相位信息不可避免地存在积分累计误差，直接导致后续处理的不确定性增大，降低阶次跟踪的效果。

Bonnardot等［14］提出了一种基于相位解调的阶次跟踪方法。该方法提取出齿轮振动信号中的啮合频率成分，基于相位解调技术获取的角度‐时间关系建立参考信号。相对于通过瞬时频率积分获取角度和时间的关系，采用相位解调做阶次跟踪不受积分累计误差的影响，在本质上更为精确。Combet等［15］对Bonnardot的研究工作做了进一步扩展，关注于将阶次跟踪过程中的参数选择自动化。然而，为了不与相邻边带重叠，该方法要求的频率分辨率很高，同时仅可以应用于很小的转速波动。为解决适用转速范围不足的缺点，Coats 等［16］提出了一种多步迭代的相位解调阶次跟踪方法。该方法从最小的可分离的转频谐波开始，通过迭代方法逐阶获取更高阶转频谐波的相位。Coats 等［17］进一步基于啮合频率进行多步迭代的相位解调，避免齿轮箱振动信号转频谐波提取困难，但是在信号存在幅值调制的时候效果并不理想。

鉴于 TLOT 方法中存在的缺点，本文致力于直接建立旋转轴的角度‐时间关系用于振动信号的等角度采样，同时适用转速变化较大的工况。首先通过带通滤波器滤出单阶的啮合频率及其边带成分，由此降低了频率分辨率的要求，同时扩大了适用的转速范围；进一步地利用啮合频率信号时域波形中的相邻波峰波谷之间存在固定的角度关系，直接建立了等角度时间序列，对应齿轮多个啮合位置。在此之前，采用 Hilbert 变换去除了包络对波峰波谷的影响。原信号基于等角度时间序列的重采样使得阶次跟踪得以实现。与 Vold‐Karman 阶次跟踪方法的对比验证了所提方法的精度。所提方法运用在一个三轴五挡的变速齿轮箱上，结果显示与参考轴相关的成分能量聚集度增加，故障诊断的准确性提高。

1 信号模型与误差分析

齿轮系统在正常无损伤情况下的振动响应成分主要是齿轮啮合频率及其谐波成分。在实际工程中，轮系不可避免地存在制造、安装误差或负载波动，啮合频率成分会出现调幅调频现象［3］，因此单级定轴齿轮的振动响应信号的角域模型可表示为：式中 A 为信号幅值；Zr为该轴齿轮的齿数；an，n，αn分别对应第 n 阶调幅边带的幅值系数、阶数和相位 ；bm，m，βm 分别对应第 m 阶啮合频率的幅值系数、阶数以及相位；式（1）表示存在 M 阶啮合频率，每阶啮合频率两侧有 N 阶转频调制边带。φ 为齿轮轴的转角，与转速的关系可表示为：式中 ω（t）为齿轮轴的角速度，与转频 fn的关系为ω=2πfn。

对时域信号的阶次跟踪，需要基于转角和时间的关系对时域信号等角度采样。在无转速计的情况下，为获取转角和时间的关系，需要对响应信号做一系列处理。首先，为消除原始信号中多阶啮合频率成分叠加的影响，对第 k 阶啮合频率及其调制成分做带通滤波，滤波过后的信号为：

滤出的信号 yk （ φ ） 包括第 k 阶啮合频率成分及其两边的调幅调频边带。其中，调幅成分和调频成分都包含齿轮轴的转角信息，这里旨在从调频部分提取转角信息，需要去除调幅成分带来的干扰。采用 Hilbert 变换去除 yk （ φ ） 信号的包络，剩下的信号y？k （ φ ）可表示为：

y？k （ φ ） 仅包括单一的啮合频率成分，同时幅值被归一化。在时域的波形中，每个相邻的波峰和波谷之间存在固定的角度关系。因此，获取 y？k （ φ ） 信号波峰和波谷对应的时间，可以建立一组等角度时间序列，用于反映齿轮轴转角随时间变化的过程［18］。求极值点令 y？k （ φ ）的一阶导数等于 0 得：式中 齿轮轴运转时，f（n t）不为 0，仅当 sin（kZrφ+βk）=0 时等式成立，φ=（iπ－βk）/（kZr）（i∈Z+）时满足条件。因此 y？k （ φ ）信号相邻的波峰波谷之间角度间隔为定值 π/（kZr）。获取波峰波谷所对应的时间可以建立等角度时间序列（φh-th），且角度序列等间隔而时间序列不等间隔。原信号 y（t）如果直接基于该角度间隔采样，对应采样阶次为 2kZr，可分析的最高阶次为 kZr，通常不满足原信号最高分析阶次的要求。通过对等角度时间序列进一步细化插值，以获取更小间隔的角度序列，增大最高分析阶次。

1. 1 物理意义

参考信号（φh-th）是一个以 π/（kZr）的角度为间隔的等角度时间序列。等同于原信号基于齿轮齿数采样，一个旋转周期（2π）等间隔采样 2kZr个数据，齿轮每转过 π/（kZr）采样一次。时变啮合刚度可以反映齿轮的转动过程。以直齿轮为例，转动过程中，单双齿啮合区间交替，如图 1 所示，B1P1及 B2P2为双齿啮合区，P1P2为单齿啮合区。一个单齿加一个双齿啮合区，即一个啮合周期的转角为 2π/Zr。齿轮转一圈经过 Zr个啮合周期。时变啮合刚度的波形可以简化为脉冲信号，大的嚙合刚度区间和小的啮合刚度区间交替。由于啮合刚度可以由多阶啮合频率谐波成分组成［19］。当对响应信号的第一阶啮合频率成分做极值搜索时，等效为齿轮每转过一个啮合周期获取两个振动数据，k=1，转过一圈即获取 2Zr个数据；对响应信号的第二阶啮合频率成分做极值搜索，k=2，齿轮每转过一圈获取 4Zr个数据，以此类推。对于锥齿轮和斜齿轮同理，啮合区间包含的齿对数可能有所变化，但也只存在一个交变区间，啮合刚度的波形都可以简化成脉冲信号。

1. 2 误差分析

假设采样频率为 fs，采样时间间隔 Δt=1/fs。由于离散采样的原因，去包络后的信号 y？k （ φ ） 实际为y？k （ hΔφ ）序列（Δφ=fnΔt）。因此对离散信号做极值搜索，实际搜索得到的极值点与理论极值点存在偏差，偏差大小与采样频率有关。采样频率越大，偏差越小。离散采样误差体现在时间序列上。因为等角度时间序列（φh-th）中，等角度序列 φh 是直接构造的，为（iπ－βk）/（kZr）（i∈Z+），极值搜索是为了获得极值点的时间，即 th。

1. 3 适用转速变化范围

当转速变化时，啮合频率将出现明显的频率模糊现象，频率模糊范围涉及到所有转频；同时，调幅的存在进一步扩大频率模糊范围。当转速变化区间很大时，不同阶的啮合频率成分相互干扰，在高阶啮合频率处这种现象愈加明显。本文方法的等角度时间序列的建立是基于单阶啮合频率谐波及其调制成分的分离，这一过程是采用带通滤波器来实现的。滤波器需要保证该阶啮合频率及其调制成分处于通带内，而其他频率成分处于阻带内。因此，本文的阶次跟踪方法需要保证所滤的第 k 阶啮合频率不与相邻啮合频率混叠。

基于上述前提，假设采样时间内信号的平均转频为 fn，最大转频变化为 Δfn，不考虑调幅因素的影响，第 k阶啮合频率成分刚好与第 k+1阶啮合频率重叠，即 kZrΔfn+（k+1）ZrΔfn=Zrfn，如图 3 所示。此时Δfn=fn/（k+2）。所提方法的运用，至少要保证第一阶啮合频率能成功滤出，即 k=1，最大转速变化范围应为 fn/3。即信号在不存在调幅的情况下，本文的阶次跟踪方法的运用需要保证在采样时间内转速变化最大不超过平均转速的 1/3。在调幅的影响下，第 k阶啮合频率右边频和第 k+1阶啮合频率的左边频会发生重叠，允许的转速变化范围会进一步缩小。

2 算法步骤和数值仿真

2. 1 算法步骤

a）对原始信号 y（t）做 FFT，选择可分离的第 k阶啮合频率区间做带通滤波，得到信号 yk （ t ）；

b）对 yk （ t ） 做 Hilbert 变 换 去 除 调 幅 包 络 的 影响，获得幅值归一化的单谐波信号 y？k （ t ）；

c）搜索 y？k （ t ） 的极值点及其所对应的时间，建立等角度时间序列（φh-th），假设该序列对应的阶次谱的最高分析阶次为 Oh；

d）根据分析的最高阶次确定采样角度间隔，对等角度序列细化插值 g 倍，利用函数拟合（φh-th），插值获得细化的等角度序列 φg所对应时间序列 tg；

e）利用函数拟合原时域响应信号，基于细化的等角度时间序列（φg-tg）对原信号插值，建立等角度采样下的振动信号；

f）对等角度采样的振动信号做傅里叶变换获取阶次谱，对应的最高分析阶次为 g Oh。

2. 2 数值仿真

以式（1）构建仿真信号。令 Zr=90，an=［0.6，0.3］，bm=［1，0.8，0.6，0.4］。不失一般性，αn=βm=0。设置的转速曲线如图 4 所示，基于数值积分获得采样时间内的平均转速为 1289 r/min。仿真信号的幅值随转速变化，假定幅值A与转速fn的关系为A=50+fn/100，理论平均幅值为 62.89 m/s2。采样频率为 20480 Hz，采样时长为 50 s，信噪比为 5 dB。仿真信号局部放大的时域图和频谱图如图 5 所示。理论上仿真信号包含 4 阶啮合频率成分及其两边的2 阶调幅边带，但是在频谱上，由于转速变化引起的频率模糊现象非常严重，无法直接识别出信号所包含的成分，不利于轮系振动状态的特征识别。

根据 2.1 节所述的步骤处理仿真信号。选择对第一阶啮合频率做带通滤波获得信号 y（1 t），滤波器范围如图 5（b）中的虚线框所示。采用的 FIR 滤波器的半阶数设为 2000。对 y（1 t）做 Hilbert 变换去除包络信号的影响，并搜索极值，如图 6 所示。相邻极值点之间的相位差为定值 π/Zr，由这些极值点可以建立等角度时间序列，对应的阶次谱最高分析阶次为 Zr。进一步地，根据分析阶次确定角度的采样间隔，对等角度序列做 10 倍细化。利用三次样条函数拟合等角度时间序列，基于细化的等角度序列插值获得对应的细化时间序列，如图 7 所示。相比于利用转速积分获取角度‐时间关系的传统方法，所提方法与给定的转速时间曲线误差更小，如图 8 所示。在 0～1 s 时，3 条曲线基本重合，表示在初期传统方法和所提方法都能较好地逼近真实的角度‐时间关系；在 49～50 s 内，点划线偏离较大，源于传统方法的误差累计。基于三次样条函数，利用所提方法的角度‐时间关系对原始信号做插值处理。建立细化的等角度采样信号，做 FFT 的阶次谱如图 9 所示。

从所提方法的阶次谱中可以清楚地看到信号成分为两阶转频阶次调制啮合频率阶次，如图 9（b）所示。阶次谱中各个成分的阶次都准确地与理论值对应，啮合频率两边对称的调制边带表明由转速变化引起的调频被消除了。啮合频率阶次及其两边调制边带阶次的幅值与理论幅值的误差如图 10 所示。

现对比基于 Vold‐Kalman 滤波器的无键相阶次跟踪方法［6］。该方法需要基于时频脊线提取方法提取转速信号作为 Vold‐Kalman滤波器的输入，同时也没有积分累计误差的过程。采用 Cost‐function‐basedRidge Detection Method （CFRD）［20］提 取 仿 真 信 号的时频脊线，获得的转速曲线如图 11 所示。随后基于 Vold‐Kalman 滤波器将仿真信号分解成单一成分信号。去除单一成分信号的包络后做 Hilbert 变换即可获取信号的角度与时间的关系。将角度时间信号作为参考信号，获取的等角度仿真信号的阶次谱如图 12 所示。阶次谱的幅值与理论幅值的误差如图 10 所示，可以看到对比方法的啮合频率阶次两边的调制边带幅值并不对称，表明转速变化引起的调频还没有被完全消除，所以带来较大的误差。

所提方法与对比方法相比，在阶次方面，二者针对仿真信号都能获得准确的阶次；在幅值方面，从图10 中可以看出，所提方法更接近理论幅值。对比方法的精度受限于所提取转速的准确程度。

3 试验数据分析

实验数据来源于图 13 所示的三轴五挡手动变速器，其结构参数如表 1 所示，传感器位于输出轴上。测试工况为：五挡输出齿轮设置了断齿故障，输入转速从 1800 r/min 降到 1500 r/min，采样频率 fs=12800 Hz，采样时间 T=40 s。竖直方向上的振动加速度响应信号时域、频域图如图 14 所示，时频图如图 15 所示。频谱当中频率混叠十分严重，无法识别单一的啮合频率谐波成分。时频图中可以看出在1000～1200 Hz 内存在共振区间。为了能够准确地识别故障特征频率成分，现采用所提方法对实验信号进行阶次跟踪。

首先挑选第一阶啮合频率做带通滤波，如图15（b）所示。滤波器的上下限频率设置为464 Hz 和575 Hz，如图 15（b）中的虚线框所示。以中间轴为参考轴，对滤波信号做 Hilbert 变换后搜索极值，建立等角度‐时间关系，对应的最高分析阶次为 30。根据等角度‐时间关系，对角度序列细化 8 倍并建立角域采样信号，对应的阶次谱如图 16 所示，最高分析阶次为240。第一级齿轮的啮合阶次（30，60，90，120）和第二级齿轮的啮合阶次（43，86，129，172）很明显。60阶次两边的边带如图17所示。主要包含四组调制成分：第一组是啮合频率成分（60阶）；第二组是以中间轴转频调制啮合频率，如61，63，64階，如图17（b）所示；第三组是以输入轴转频调制啮合频率，如61.58，63.16阶，如图17（b）所示；第四组是输出轴的冲击故障特征频率，如图17（a）所示。阶次谱中啮合频率成分及其边带特征明显，频谱聚集度高，便于齿轮系统故障的识别。

运用对比方法处理实验信号，阶次谱如图18和19所示，可以大致地找到两组啮合阶次谐波以及60阶次附近的四组调制成分。但是，由于依然存在频率模糊，响应信号中成分所对应的阶次与理论存在一定偏差，如啮合阶次；各阶次的幅值也与对比方法相差较大，能量不够聚集。所提方法能更好地消除变转速引起的频率模糊现象。另外，对比方法需要进行大规模的解耦计算，计算效率更低。在MATLAB版本为R2018a，CPU为IntelCorei7‐8700及运行内存8GB的条件下，仿真计算中所提方法求解耗时 15 s，对比方法求解耗时5082 s；实验中所提方法求解耗时 8 s，对比方法求解耗时 33134 s。

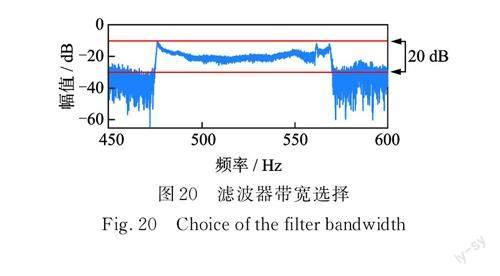
滤波器带宽的选择也影响所提方法的应用。在仿真信号中，第一、二阶啮合频率所属的两块区域之间间隔明显，如图5（b）所示，因此可以手动挑选中间过渡带的一个区域设置为滤波器的边界。在实验信号中，根据短时傅里叶变换检查出啮合频率区域大概的范围，如文中转速从1800r/min降到1500r/min，大致对应的常啮合齿轮副啮合频率范围为570～475Hz。但是，并不能直接将该区域设定为滤波器的范围，因为可能存在不同啮合频率区域的重叠，同时啮合信号还存在调幅成分。因此还需要根据信号的频谱进一步判断。文献［16］表明，区域中最高幅值和最低幅值之间相差20dB可以划分为一个啮合频率区间。因此，如图20所示，以475～570Hz中的最高幅值为上界，与其相差20dB的幅值为下界，在纵轴上画出一个区域；以高于下界的两个横轴区域之间为过渡带，在过渡带中选择464Hz和575Hz为滤波器的上下限。

4 结论

本文提出了一种基于极值搜索的无键相阶次跟踪方法，可用于变速工况下齿轮系统的故障诊断。该方法利用单一啮合频率信号的相邻波峰波谷之间存在固定的角度间隔，直接建立参考轴的转角时间序列，避免了由转速积分导致的累计误差。单一啮合频率成分的分离通过带通滤波器来实现，Hilbert变换去除包络对啮合频率波峰波谷的影响。随后振动响应信号可以基于细化的等角度时间序列重采样。与对比方法相比，所提方法对原信号的幅值恢复精度更高，同时处理方法简单，计算效率高。实验表明所提方法可以极大地增强变速工况下齿轮传动系统的特征识别及故障诊断的准确性。

参考文献：

［1］任凌志，于德介，彭富强，等.基于多尺度线调频基稀疏信号分解的齿轮故障信号阶比分析［J］.机械工程学报，2011，47（13）：92-97.

RenLingzhi， Yu Dejie， Peng Fuqiang， et al. Orderanalysis of gear fault signals based on multi-scale chirpletand sparse signal decomposition［J］. Journal of Mechani‐cal Engineering，2011，47（13）：92-97.

［2］ Chen Y J， Liang X H， Zuo M J. Sparse time seriesmodeling of the baseline vibration from a gearbox undertime-varying speed condition［J］. Mechanical Systemsand Signal Processing，2019，134：106342.

［3］ Yang X， Ding K， He G. Phenomenon-model-basedAM-FM vibration mechanism of faulty spur gear［J］.Mechanical Systems and Signal Processing， 2019，134：106366.

［4］ Havard V， Jan L. High resolution order tracking at ex‐treme slew rates using Kalman tracking filters［J］.Shock and Vibration，1995，2（6）：507-515.

［5］ 邓 蕾 ，傅 炜 娜 ，董 绍 江 ，等 . 无 转 速 计 的 旋 转 机 械Vold-Kalman 阶比跟踪研究［J］. 振动与冲击，2011，30（3）：5-9.

Deng Lei， Fu Weina， Dong Shaojiang， et al. TacholessVold-Kalman order tracking of rotating machinery［J］.Journal of Vibration and Shock，2011，30（3）：5-9.

［6］ Wang Y， Xie Y， Xu G， et al. Tacholess order-trackingapproach for wind turbine gearbox fault detection［J］.Frontiers of Mechanical Engineering，2017，12（3）：427-439.

［7］ Angle S， Martin R， Ruben P， et al. Harmonic ordertracking analysis： a speed-sensorless method for condi‐tion monitoring of wound rotor induction generators［J］.IEEE Transactions on Industry Applications，2016，52（6）：4719-4729.

［8］ Xu T， Wu X. Fast tracking algorithm based on Gabortransformation［J］. Computer Engineering and Applica‐tions，2016，52（6）：134-138.

［9］ 林京，趙明 . 变转速下机械设备动态信号分析方法的回顾与展望［J］. 中国科学：技术科学，2015，45（7）：669-686.

Lin Jing， Zhao Ming. Dynamic signal analysis for speedvarying machinery： a review［J］. Scientia Sinica Tech‐nologica，2015，45（7）：669‐686.

［10］ Fyfe K R， Munck E D S. Analysis of computed ordertracking［J］. Mechanical Systems and Signal Process‐ing，1997，11（2）：187-205.

［11］ 江星星，李舜酩，周东旺，等 . 时频脊融合方法及时变工况行星齿轮箱故障识别［J］. 振动工程学报，2017，30（1）：127-134.

Jiang Xingxing， Li Shunming， Zhou Dongwang， et al.Time-frequency ridge fusion method and defective iden‐tification of planetary gearbox running on time-varyingcondition［J］. Journal of Vibration Engineering，2017，30（1）：127-134.

［12］ He G， Ding K， Li W， et al. A novel order trackingmethod for wind turbine planetary gearbox vibrationanalysis based on discrete spectrum correction tech‐nique［J］. Renewable Energy，2016，87（1）：364-375.

［13］ Wang H， Chen P. Fuzzy diagnosis method for rotatingmachinery in variable rotating speed［J］. IEEE SensorsJournal，2011，11（1）：23-34.

［14］ Bonnardot F， El Badaoui M， Randall R B， et al. Useof the acceleration signal of a gearbox in order to per‐form angular resampling （with limited speed fluctua‐tion）［J］. Mechanical Systems and Signal Processing，2005，19（4）：766-785.

［15］ Combet F， Gelman L. An automated methodology forperforming time synchronous averaging of a gearbox sig‐nal without speed sensor［J］. Mechanical Systems andSignal Processing，2007，21（6）：2590-2606.

［16］ Coats M D， Randall R B. Order-tracking with and with‐out a tacho signal for gear fault diagnostics［C］. Pro‐ceedings of Acoustics. Fremantle，2012：1-6.

［17］ Coats M D， Randall R B. Single and multi-stage phasedemodulation based order-tracking［J］. Mechanical Sys‐tems and Signal Processing，2014，44（1-2）：86-117.

［18］ 曾智杰 . 行星齒轮系统振动信号传递机理与非平稳信号角域分析方法［D］. 广州：华南理工大学，2019.

Zeng Zhijie. Vibration signal transfer mechanism of plan‐etary gear system and angular analysis method of nonstationary signal［D］. Guangzhou： South China Univer‐sity of Technology，2019.

［19］ Liang X， Zuo M J， Feng Z. Dynamic modeling of gear‐box faults： a review［J］. Mechanical Systems and Sig‐nal Processing，2018，98：852-876.

［20］ Liu H， Cartwright A N， Basaran C. Moiré interfero‐gram phase extraction： a ridge detection algorithm forcontinuous wavelet transforms［J］. Applied Optics，2004，43（4）：850-857.