时滞反馈下非正交面齿轮主共振特性的多尺度法研究

莫帅 张应新 罗炳睿 岑国建 黄云生

摘要： 非正交面齿轮传动可以满足轴交角在 0°到 180°之间任意角的非正交传动形式，建立了含时滞反馈的非正交面齿轮传动系统的非线性动力学模型，考虑了时变啮合刚度、传动误差、齿侧间隙和输入扭矩波动等因素。此外，采用多尺度法对系统的主共振特性进行分析，判定了系统的主共振稳定性条件。用数值方法分析了时滞控制参数、啮合阻尼、时变啮合刚度波动幅值和载荷波动对系统幅频特性的影响。结果表明：在控制过程中应合理选择控制参数以避免主共振振幅过大和产生不稳定分支；适当的啮合阻尼有利于抑制系统主共振的振幅和缩减不稳定分支；过高的激励频率易产生主共振的不稳定分支；主共振的不稳定分支随着啮合刚度的波动的增加逐渐缩减，但是在激振频率接近主共振频率时，较小的啮合刚度波动也会导致系统失稳；载荷波动的增加会导致系统主共振幅值增加，对系统的稳定性造成损害。

关键词： 非线性动力学；主共振；非正交面齿轮；多尺度法；稳定性；时滞反馈

中图分类号： O322；TH132.41 文獻标志码： A 文章编号： 1004-4523（2023）03-0623-11

DOI：10.16385/j.cnki.issn.1004-4523.2023.03.004

引 言

非正交面齿轮传动系统可以满足轴交角在 0°到180°之间任意角的非正交传动形式，同时其所特有的对轴向安装误差不敏感和无轴向力的结构优势使其在高速重载的航空领域和小模数传动领域具有十分广泛的应用价值。齿轮系统具有丰富的非线性行为，因此对非正交面齿轮系统的振动进行控制并提高系统的可靠性具有重要的工程意义。各种受控动力系统的控制环节都不可避免地存在时滞，对于许多时滞系统，如果忽略其时滞会得到错误的结论，因此随着控制速度和要求的不断提高，控制过程中的时滞现象成为不容忽视的问题。多尺度法可以分析稳态响应的稳定性，描绘非自治系统的全局运动性态，这是多尺度法被引入到齿轮系统稳定性分析里的一个重要原因。

近年来，国内外学者对齿轮系统的主共振特性和稳定性做了大量深入的研究。文献［1］分析了有裂纹齿轮系统的参数共振和稳定性，并在此基础上采用多尺度法揭示了阻尼比等关键参数对齿轮系统稳定性的影响。文献［2］使用多尺度法研究了包括齿侧间隙等非线性因素在内的单自由度齿轮系统的受迫振动响应。文献［3］采用多尺度法对直齿圆柱齿轮的主共振特性做了深入研究。对于不稳定的系统，振动会不断增大直到系统被损坏，因此稳定性是系统必备的条件。文献［4？5］从不同方面阐述了多种因素对齿轮系统稳定性的影响，并提出了保证系统稳定性的理论和方法。文献［6］对含裂纹、点蚀等缺陷的故障齿轮的振动特性做了详细论述。文献［7］建立了随机波动模型来模拟风力机齿轮传动系统的外激励，用数值方法探讨了随机风及随机侧隙因素影响下系统的稳定性。文献［8？10］讨论了面齿轮分流传动系统和行星轮系的均载特性，从一个新的角度研究了齿轮系统的稳定性。文献［11］提出了一种使用双变化时间步长的算法，将小齿轮的速度和拖曳转矩作为激励源来分析润滑剂对齿轮系统振动的影响。

从已有文献来看，大部分研究聚焦于传统齿轮构型的振动特性和稳定性，而非正交面齿轮作为一

种由渐开线圆柱齿轮和圆锥齿轮啮合传动的新型传动构型，对其稳定性和振动特性的研究则相对较少，并且目前综合考虑主动控制参数和系统参数对振动特性影响的研究较少。

本文的主要目的是对含时滞反馈的非正交面齿轮的主共振特性进行研究，首先建立系统动力学模型，其中考虑了时变啮合刚度、传动误差、齿侧间隙和载荷波动等因素。随后采用多尺度法判定了系统的稳定性条件。最后采用数值方法研究了系统参数对系统幅频特性的影响。

1 非正交面齿轮系统动力学模型

1. 1 非正交面齿轮系统模型

如图 1 所示为非正交面齿轮传动系统模型，两坐标系的 Y 轴在 O 点重合，方向为垂直纸面向外。非 正 交 面 齿 轮 坐 标 系 O？X1Y1Z1 由 直 齿 轮 坐 标 系O？X2Y2Z2绕轴线 OY2旋转 γm得到，直齿轮轴线与坐标轴 OX2重合，非正交面齿轮轴线与坐标轴 OZ1重合，坐标系原点建立在两轴线的交点处。γm与轴交角 γ 满足 γm = 180°- γ。

1. 2 非正交面齿轮时变啮合刚度

由于面齿轮副在实际啮合过程中发生一对齿啮合与两对齿啮合的交替，因此齿轮副的啮合刚度随啮合齿数的周期性变化而变化。

本节通过有限元加载的方法求取面齿轮副的时变啮合刚度。建立如图 2 所示的非正交面齿轮副的有限元模型。为了减少不必要的计算量，只对五对轮齿进行计算。图 2 中 O 为齿轮轴线的交点，O1为非正交面齿轮底面与轴线的交点，O2为直齿轮的几何中心。求解过程设置了 3 个分析步，在第 1 个分析步中，对直齿轮施加微小转动量，面齿轮保持固定，使齿面接触，对面齿轮施加载荷，幅值为创建的 0？1平滑分析步；在第 2 个分析步中，释放面齿轮旋转自由度，面齿轮载荷幅值修改为 Ramp；在第 3 个分析步中，对直齿轮施加转动量，使直齿轮转过大约 5 个齿数，面齿轮载荷保持不变。

由于齿轮的刚度与齿轮的形状和载荷有关，其关系可表示为：

K m （ t ）= F （ t ） /xn （1）式中 xn表示轮齿间相对位移，由载荷作用下的传动误差 LTE 和法向静态传动误差 e（t）共同作用产生，可表示为：xn = LTE - e （ t ）=（r2 θ 2 - r1 θ 1 ） cos αn - e （ t ） （2）

用有限元方法求解载荷作用下的法向接触力F（t）和两个传动误差 LTE，e（t），根据式（1）便可得到时变啮合刚度的变化曲线。对有限元计算结果进行处理，首先提取啮合刚度的最大值和最小值，得到简化的矩形波形式的时变啮合刚度曲线，如图 3 中蓝色曲线所示；进而对矩形波形式的时变啮合刚度进行傅里叶拟合，一般只取到前 5 阶，得到更为精确的时变啮合刚度曲线，如图 3 中红色曲线所示。由此，可将非正交面齿轮副的时变啮合刚度表示为：式中 Ka为矩形波形式时变啮合刚度的幅值；ωm为啮合角频率，其值等于输入轴转速频率 ωs与输入齿轮齿数 Z2之积；kri为第 i 阶分量的波动幅值；Nk为傅里叶级数的阶数，本文中 Nk=5；φri 为第 i 阶分量的相位角。

1. 3 非正交面齒轮振动微分方程

如图 4 构建非正交面齿轮传动系统的扭振模型，将传动误差、时变啮合刚度、齿侧间隙、输入扭矩的波动等因素引入到该系统的振动模型。

假设轴承和轴的支撑刚度远远大于齿轮的啮合刚度，用啮合线方向上的等效位移 xn作为新的自由度来代替系统的两个扭转自由度 θ1和 θ2。非正交面齿轮副因振动和传动误差产生的啮合线方向位移可表示为式（2），式中，r1为直齿轮的分度圆半径，r2为非正交面齿轮齿宽中点到回转轴的距离。αn为齿轮副 的 法 向 压 力 角 。 e（t）可 表 示 为 e （ t ）= e a +er sin （ ω m t + φ0 ），其中，e a 为静态误差，er 表示误差的波动，φ0 为误差波动的相位。

将啮合线方向的位移 xn 视为唯一的自由度，得到系统振动微分方程：

取 bm为无量纲化标尺，对式（3）进行无量纲化，并将外载荷波动分解为一个常值项与一个波动项之和，得到：

本文考虑了施加主动控制后非正交面齿轮系统的时滞现象，时滞意味着系统当前状态的变化依赖于系统的过去。对于本文所研究的含时滞非正交面齿轮系统，在系统支撑处施加位移和速度的时滞反馈控制，将时滞反馈模型引入到系统的振动微分方程（4）中［12］。可得到：式中 位移时滞量 xˉ n （ τ - τd ） 在位移反馈回路中，表示非正交面齿轮系统啮合线上等效位移 xˉ n 在施加主动控制前后所表现出的时间差，其对应的位移控制量为 gd；速度时滞量 xˉ？ n （ τ - τ v ）在速度反馈回路中，表示非正交面齿轮系统啮合线上相对速度 xˉ？ n 在施加主动控制前后所表现出的时间差，其对应的速度控制量为 gv。

2 主共振特性时间多尺度法分析

该部分采用时间多尺度法对非正交面齿轮副扭转振动的主共振特性进行分析，其基本思路是将系统响应的展开式考虑为多个时间尺度的函数。

对含时滞反馈的系统振动微分方程（5）中的无量纲化齿侧间隙函数 f （ xˉ n ） 进行拟合［13］，三次多项式 已 经 能 够 精 确 反 映 系 统 啮 合 状 态 ：f （ xˉ n ）=δ1 xˉ n + δ2 xˉ 3n = δ1 （ xˉ n + δ0 xˉ 3n ），其中 δ1与系统固有频率 ω0满足 ω0 = δ1 。

引入 Ti = εiτ 表示不同尺度的时间变量，其中？ε？？1。不同的时间尺度描述了变化过程中的不同节奏，阶数越低，变化越缓慢，阶数越高，变化越迅速。将系统振动微分方程（5）的解表示为不同尺度时间变量的函数：式中 m 表示小参数 ε的最高阶次，其值取决于计算的精度要求。将不同尺度的时间变量 Ti视为独立的变量，xˉ n 可视为 m 个时间变量的函数。

对系统的主共振的稳定性进行分析。将方程（18）在 （ αˉ，φˉ ） 处线性化，形成关于扰动量 Δα 和 Δφ的微分方程：

3 非正交面齿轮主共振特性研究

为了研究非正交面齿轮传动系统的振动特性，本节探讨了控制参数、啮合阻尼、啮合刚度波动和载荷波动对系统主共振的影响。根据系统的物理参数定 义 方 程（20）的 初 始 无 量 纲 参 数 ：啮 合 阻 尼 ζm=0.05，时变啮合刚度波动幅值 κ=0.3，无量纲化后的静载荷 f0=0.1，动载荷波动幅值 f=0.3。位移反馈gd=0.2，速 度 反 馈 gv= ？ 0.2。 时 间 迟 滞 τd= τv=T/9。

3. 1 时滞参数对主共振特性的影响

方程（20）的其他参数取初始参数，使位移控制参数 gd从？0.2 变化到 0.2。图 5（a）给出以 gd为参数的幅频特性曲线族，可以观察到，随着 gd的增加，系统 主 共 振 达 到 峰 值 所 对 应 的 频 率 减 小 。 当 gd 从？0.2 增加到？0.1 时，主共振幅值降低，但是随着 gd继续增加，在 gd=0 和 gd=0.1 时，主共振的振幅激增，且存在较大的不稳定分支如图 5（a）中虚线所示。当 gd取 0.2 时，不稳定分支消失，且振幅降低。这表明当其他参数取初始值时，控制参数 gd取 0 或0.1 会导致系统稳定性变差。

图 5（b）给出了以 ω 为参数的幅频特性曲线族，描述了控制参数 gd随振幅 α 的变化关系。随着激励频率 ω 增加，系统主共振达到峰值所对应的 gd值减小，并且当 ω 取 1.075 和 1.1 时，系统主共振的幅频曲线出现不稳定分支，即振幅 α 产生多值。以 ω=1.1为例，图 5（b）中虚线框内为 ω=1.1 时振幅 α 发生跳跃的区域。当 gd增加时，振幅 α 沿曲线 gd？α 变化，到达 A1点时发生从 A1到 A3点的跳跃现象。这个过程反过来，即当 gd逐渐减小时，振幅 α 会从 A4点到 A2点突变。这种曲线多值现象对应于系统的不稳定状态，因此当系统工作在主共振频率附近时，应控制参数 gd使其避开 gd？α 曲线的多值区域。

本文用啮合力和齿间加速度来验证多尺度方法求解该系统的可行性。求解系统振动微分方程（5）后，将系统位移响应和速度响应回代至振动微分方程得到啮合力和齿间加速度随系统参量变化的规律。图 6 给出了位移控制参数 gd对啮合力和齿间加速度的影响，可以看出，随着 gd的增大，啮合力总体上呈逐渐增加的状态；且 gd>0.092 时，系统的齿间加速度随 gd的变化急剧增加。图 5 和图 6 表明，为了避免对系统主共振的稳定性造成损害以及避免过高的啮合力和齿间相对加速度，系统的位移控制参数gd应控制在小于 0 的范围内。

方程（20）的其他参数取初始参数，使速度控制参数 gv从？0.2 变化到 0.2。可以得到和位移参数 gd变化类似的结果：如图 7（a）所示，系统主共振达到峰值所对应的频率随着 gv 的增加而增加 ，并且在gv=0.1 和 gv=0.2 时，主共振的振幅激增，存在较大的不稳定分支，造成系统失稳。因此在控制过程中，当系统其他参数取初始值时，控制参数 gv取 0.1 或0.2 会损害系统的稳定性。图 7（b）所示为以 ω 为参数的幅频特性曲线族，系统主共振达到峰值所对应的 gv值随着激励频率 ω 的增加而减小，并且当 ω 取1.075 和 1.1 时，系统主共振的幅频曲线出现不稳定分支，表明系统即将失稳，图中虚线框内表示 ω=1.1 时的振幅跳跃区域，gv增加时振幅 α 从 A4突变到A1，gv减小时振幅 α 从 A2突变到 A3。

圖 8 给出了速度控制参数 gv对啮合力和齿间加速度的影响，可以看出，当 gv∈（？1，？0.6）时，啮合力逐渐增加而齿间加速度逐渐降低，当 gv∈（？0.6，0.1）时，啮合力和加速度的变化趋于平缓，当 gv>0.1时，啮合力和加速度都有剧烈的波动。

图 7 和 图 8 表 明 系 统 的 速 度 控 制 参 数 应 在（？0.6，0）内取值，以保证啮合力和齿间相对加速度不会剧烈波动，以及避免系统主共振振幅过高和产生较大的不稳定分支。

方程（20）的其他参数取初始参数，使位移时滞τd从 0 变化到 4T/9。图 9（a）给出以 τd为参数的幅频特性曲线族，可以观察到，随着 τd的增加，系统主共振 达 到 峰 值 所 对 应 的 激 励 频 率 增 加 ，并 且 当 τd 取2T/9 和 T/3 时，系统振幅显著降低，图 9（a）中虚线所示的不稳定分支明显缩减，当 τd<2T/9 或 τd>T/3时，系统振幅较大且都存在较大的不稳定分支，这表明当 τd取 2T/9 和 T/3 时系统主共振达到较好的稳定状态，在控制过程中应选取合理的位移时滞 τd，避免使系统振幅过高和产生不稳定分支，保证系统稳定性。

图 9（b）给出了以 ω 为参数的幅频特性曲线族，描述了位移时滞 τd 随振幅 α 的变化关系。可以看出，随着激励频率 ω 的增加，系统主共振的振幅 α 的不稳定多分支愈发扩张，表现为曲线愈发明显地出现多值。以 ω=1.2 为例，图 9（b）中虚线框内为 ω=1.2 时振幅 α 发生跳跃的区域。随着 τd增加，振幅 α沿 τd？α 曲线逐渐降低，经过 A1点时发生从 A1到 A3点的跳跃现象；同样地，当 τd减小时，振幅 α 发生从 A4到 A2点的跳跃。

图 10 给出了位移时滞 τd对啮合力和齿间加速度的影响，当 τd >3.47 时，系统的啮合力和齿间相对加速度发生剧烈波动。图 9 和图 10 表明位移时滞 τd可以降低主共振振幅和缩减系统的不稳定分支，有益于系统的稳定性，但是若位移时滞 τd过大会导致系统啮合力和齿间加速度剧烈波动，对系统稳定性造成损害。

方程（20）的其他参数取初始参数，使速度时滞τv从 0 变化到 4T/9。由图 11（a）的幅频特性曲线族可以看出，当 τv取 T/3 和 4T/9 时，主共振振幅大幅增加，且具有较大的不稳定分支。这表明当系统其他参数取初始值时，τv取 T/3 和 4T/9 会对系统稳定性造成损害。图 11（b）所示为以 ω 为参数的幅频特性曲线族，随着 ω 增加，曲线愈发明显地出现多值现象，表明系统主共振的振幅 α 不稳定的区域愈发增大，意味着系统更容易失稳。图 11（b）中虚线框内表示 ω=1.2 时的振幅跳跃区域，τv增加时振幅 α 从A4突变到 A2，τv减小时振幅 α 从 A1突变到 A3。

图 12 给出了速度时滞 τv对啮合力和齿间加速度的影响，当 τv >2.42 时，系统的啮合力和齿间相对加速度发生剧烈波动。图 11 和图 12 表明适当的速度时滞 τv可以降低系统主共振的振幅，但是若 τv取值过大会导致系统主共振振幅激增，产生较大的不稳定分支，且会造成系统的啮合力和齿间加速度的剧烈波动。

3. 2 啮合阻尼对主共振特性的影响

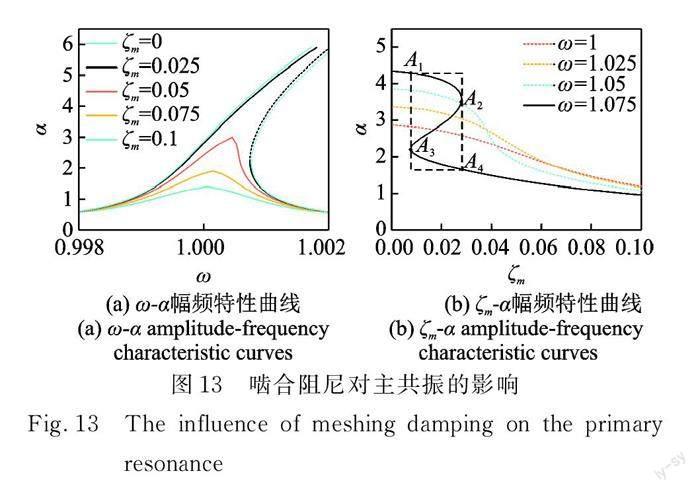
方程（20）的其他参数取初始参数，使啮合阻尼ζm从 0 变化到 0.1。图 13（a）给出以 ζm为参数的幅频特性曲线族。当 ζm取 0 和 0.025 时，系统存在如图中虚线所示的不稳定分支。随着 ζm的增大，系统主共振的振幅 α 下降，且不稳定分支逐渐缩小。当 ζm取0.05，0.075和 0.1时，不稳定分支消失，这表明可以通过适当增加系统的啮合阻尼来提升系统的稳定性。

图 13（b）给 出 了 以 ω 为 参 数 的 幅 频 特 性 曲 线族，描述了系统啮合阻尼 ζm 随振幅 α 的变化关系。当激励频率小于系统共振频率，即 ω 取 1 和 1.025时，系统主共振的振幅 α 随 ζm的增大而降低；当激励频率大于系统主共振频率，即 ω 取 1.05 和 1.075 时，系统主共振的幅频曲线出现不稳定分支，即振幅 α产生多值。图 13（b）中的虚线框内为 ω=1.075 时振幅 α 发生跳跃的区域：当 ζm增加时，振幅 α 沿 ζm？α 曲线降低，经过 A1点时，发生从 A1点到 A3点的跳跃现象，此时振幅突然降低，经过 A3点后 α 继续沿 ζm？α 曲线降低。当 ζm逐渐减小时，振幅 α 会发生从 A4点到A2点的突变。

啮合阻尼对系统啮合力和齿间加速度的影响如图 14 所示。可以看出，当啮合阻尼 ζm较小时，系统有较大的啮合力和齿间相对加速度。ζm的增加对降低啮合力和齿间相对加速度有明显的效果，且随着啮合阻尼的增加，啮合力和齿间加速度的变化逐渐趋于平缓。

13 和图 14 表明：适当地增加系统的啮合阻尼可以有效地抑制系统的主共振振幅，缩减不稳定分支，并且避免系统啮合力和齿间相对加速度的急剧变化。

3. 3 啮合刚度波动对主共振特性的影响

方程（20）的其他参数取初始参数，使啮合刚度波动幅值 κ 从 0.2 变化到 1。图 15（a）给出了以 κ 为参数的幅频特性曲线族，可以看出，当 κ 取 0.2，0.4和 0.6 时，系统存在如图中虚线所示的不稳定分支。随着 κ 的增大，系统主共振的振幅下降，且不稳定分支逐渐缩减。

图 15（b）给 出 了 以 ω 为 参 数 的 幅 频 特 性 曲 线族，描述了系统啮合刚度波动幅值 κ 随振幅 α 的变化关系。当激励频率大于系统主共振频率，即 ω 取1.05 和 1.075 时，系统主共振幅频曲线出现不稳定分支，即振幅 α 产生多值。以 ω=1.075 为例，图 15（b）中虚线框内为 ω=1.075 振幅 α 发生跳跃的区域，当κ 增加时，振幅 α 沿曲线 κ？α 变化，到达 A1点时发生从 A1到 A3点的跳跃现象。当 κ 逐渐减小时，振幅 α会发生从 A4 点到 A2 点的突变。同时观察到，ω=1.075 发生跳跃的区域所对应的 κ 值比 ω=1.05 时小，这表明激振频率接近主共振频率时，幅频特性曲线越容易出现多值，此时较小的啮合刚度波动也容易导致系统的不稳定。

啮合刚度的波动对系统啮合力和齿间加速度的影响如图 16 所示。可以看出，当啮合刚度波动量 κ小于 0.57 时，系统的啮合力和齿间相对加速度随着κ 的增加逐渐降低，当啮合刚度波动量 κ 大于 0.57时，系统的啮合力开始逐渐上升，且齿间相对加速度急剧增加。

图 15 和图 16 说明，适当增加啮合刚度的波动可以改善系统的动力学特性，降低主共振幅值，缩减系统的不稳定分支以及降低传动过程中的啮合力和齿间加速度。但当系统处于不稳定区域内，较小的啮合刚度波动也会导致振幅的突变。

3. 4 载荷波动对主共振特性的影响

方程（20）的其他参数取初始参数，使载荷波动幅值 f 从 0 变化到 0.5。图 17（a）给出以 f 为参数的幅频特性曲线族，当 f=0.1 时，系统主共振的稳态幅值较小，不存在不稳定分支；当 f 从 0.2 变化到 0.5 时，主共振的振幅急剧增加，存在如图中虚线所示的不稳定分支。随着 f 的增大，系统主共振的振幅增大，不稳定分支扩张。这表明外激励载荷过大会造成系统主共振的稳态幅值增加，并且对系统的稳定性造成损害。因此当系统工作在接近主共振状态时，应该避免过大的载荷激励。

图 17（b）给 出 了 以 ω 为 参 数 的 幅 频 特 性 曲 线族，描述了系统外载荷激励的波动幅值 f 随振幅 α 的变化关系。可以观察到，当激励频率大于系统主共振频率，即 ω 取 1.05 和 1.075 时，系统主共振的幅频曲线出现不稳定分支，即振幅 α 产生多值。以 ω=1.075 为例，图 17（b）中的虚线框内为 ω=1.075 时振幅 α 发生跳跃的区域。当 f 增加时，振幅 α 沿曲线 f？α增加，经过 A4点时发生从 A4到 A2点的跳跃现象，α继续沿曲线 f？α 增加。当 f 逐渐减小时，振幅会发生从 A1点到 A3点的突变。同时可以观察到，激励载荷f 越大，激振频率 ω 越高，振幅 α 的多值现象越明显，即系统的不稳定现象越明显。

载荷波动对系统啮合力和齿间加速度的影响如图 18 所示。可以看出，随着载荷波动的增加，齿间啮合力急剧增加且齿间相对加速度大幅度波动。

图 17 和圖 18 说明，载荷波动越大，主共振振幅越大，不稳定分支愈发扩张，且会造成啮合力激增和齿间加速度的剧烈波动，这无疑会对系统的稳定性造成损害。因此在实际工况中，应对系统的载荷加以限制以保证系统的稳定性。

选取如表 1 所示的三组时滞参数，分别代表不对系统做时滞反馈控制、对系统做合理的反馈控制和时滞参数选取不合理三种情况。其他参数按第 3节定义的初始参数选取，在 MATLAB 中采用 dde23命令求解含时滞微分方程（5）的响应，可得到如图19～21 所示的时间历程图和系统相图。

由图 19（a）可以看出，当不对系统做时滞反馈控制时，系统在 τ>150 后逐渐收敛到周期运动状态；对系统加入合理的时滞反馈控制时，系统响应的时间历程图如图 20（a）所示，可以看出，合理的时滞反馈控制参数可以使系统响应快速地收敛到周期运动状态。

当系统的时滞反馈控制参数选取不合理时，系统响应的时间历程图如图 21（a）所示，可以看出，此时系统响应不仅不会收敛到稳定解，反而会随时间的增加逐渐发散，导致系统的稳定性变差，由图 21（b）的相图可以看出，此时系统进入混沌状态。因此在控制过程中，应选取合理的时滞参数，避免对系统稳定性造成损害。

4 结 论

本文建立了非正交面齿轮传动系统的非线性动力学模型，采用多尺度法对系统的主共振特性进行分析，用数值方法分析了时滞参数、啮合阻尼、时变啮合刚度波动幅值和载荷波动对系统幅频特性的影响。结论表明：

（1）在控制过程中，系统的稳定性并不与时滞控制参数呈线性关系，应合理选择控制参数，将位移控制参数 gd和速度控制参数 gv限制在小于 0 的范围内，避免主共振振幅过大和产生不稳定分支，保证系统的稳定性。

（2）啮合阻尼有利于抑制振幅幅值过高，对缩减不稳定分支和防止振幅的跳跃具有明显的帮助。因此可以选取合适的润滑方式，适当增大阻尼，抑制系统在共振频率附近的响应峰值。

（3）载荷的波动会导致系统的不稳定，系统的振幅会随载荷波动幅值的增加而增加；对于啮合刚度，虽然随着啮合刚度的增加振幅会减小，但是当系统处于不稳定区域内，较小的啮合刚度波动也会导致振幅的突变。可以采用改善齿轮表面微观形貌及粗糙度的方法使时变啮合刚度波动趋于平缓。

（4）激励频率越大，幅频曲线越容易出现不稳定分支，系统振幅增加，且跳跃区域扩大，造成系统失稳。

参考文献：

［1］ WANG J G，LV B，SUN R，et al. Resonance and stabil？ity analysis of a cracked gear system for railway locomo？tive［J］. Applied Mathematical Modelling，2020，77（1）：253-266.

［2］ Moradi H， Salarieh H. Analysis of nonlinear oscilla？tions in spur gear pairs with approximated modelling of backlash nonlinearity［J］. Mechanism and Machine The？ory，2012，51（1）：14-31.

［3］ 石慧荣，赵冬艳，李宗刚，等 . 含时滞反馈控制的直齿圆柱齿轮主共振分析［J］. 振动与冲击，2019，38（21）：91-96.

SHI Huirong， ZHAO Dongyan， LI Zonggang， et al.Primary resonance analysis for a spur gear system with time delay feedback control［J］. Journal of Vibration and Shock，2019，38（21）：91-96.

［4］ LIU C Z，QIN D T，WEI J，et al. Investigation of non？linear characteristics of the motor-gear transmission sys？tem by trajectory-based stability preserving dimension reduction methodology［J］. Nonlinear Dynamics，2018，94（3）：1835-1850.

［5］ HU Z H，TANG J Y，CHEN S Y. Analysis of coupled lateral-torsional vibration response of a geared shaft ro？tor system with and without gyroscopic effect［J］. Pro？ceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science，2018，232（24）：4550-4563.

［6］ WANG X. Stability research of multistage gear trans？mission system with crack fault［J］. Journal of Sound and Vibration，2018，434（1）：63-77.

［7］ CHEN H T，WANG X H，GAO H C，et al. Dynamic characteristics of wind turbine gear transmission system with random wind and the effect of random backlash on system stability［J］. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical En？gineering Science，2017，231（14）：2590-2597.

［8］ MO S，ZHANG T，JIN G G，et al. Analytical investiga？tion on load sharing characteristics of herringbone plane？tary gear train with flexible support and floating sun gear［J］. Mechanism and Machine Theory，2020，144（2）：1-27.

［9］ 莫帥，岳宗享，冯志友，等 . 面齿轮分汇流系统动力学均 载 特 性 研 究［J］. 华 中 科 技 大 学 学 报（自 科 学 版），2020，48（2）：23-28.

MO Shuai， YUE Zongxiang， FENG Zhiyou， et al. An？alytical investigation on load sharing characteristics for face gear split flow system［J］. Journal of Huazhong University of Science & Technology （Natural Science Edition），2020，48（2）：23-28.

［10］ 莫帅，岳宗享，冯志友，等 . 面齿轮-行星传动串联系统固 有 特 性 研 究［J］. 华 中 科 技 大 学 学 报（自 科 学 版），2020，49（1）：24-30.

MO Shuai， YUE Zongxiang， FENG Zhiyou， et al. Re？search on natural characteristics of face gear-planetary gear compound transmission system［J］. Journal of Hua？zhong University of Science & Technology （Natural Science Edition），2020，49（1）：24-30.

［11］ LIU F H，ZHANG L，YU X H. Stability investigation of velocity-modulated gear system using a new computa？tional algorithm［J］. Nonlinear Dynamics，2017，89（2）：1111-1128.

［12］ PENG J，WANG L H，ZHAO Y Y，et al. Bifurcation analysis in active control system with time delay feed？back［J］. Applied Mathematics and Computation，2013，219（19）：10073-10081.

［13］ MORADI H，SALARIEH H. Analysis of nonlinear os？cillations in spur gear pairs with approximated modelling of backlash nonlinearity［J］. Mechanism and Machine Theory，2012，51（1）：14-31