基于自抗扰控制的电控机械式制动器弯道制动力控制策略研究*

白芳华 张强 郭雅各 徐海澜 白中浩

（1.招商局检测车辆技术研究院有限公司，重庆 401329；2.湖南大学，湖南大学车辆安全研究中心，长沙 410082）

主题词：主动安全 电控机械式制动器 制动力控制 弯道 自抗扰控制

1 前言

汽车在弯道工况下制动时，在制动力和离心力的作用下，垂直载荷会在汽车前、后轴和左、右轮之间发生转移，极易发生转向不足和转向过度等现象，导致车辆操纵稳定性不佳[1]。电控机械式制动器（Electro Mechanical Brake，EMB）克服了传统制动系统无法实现主动制动以及无法精确控制制动压力的缺点，可有效避免车辆打滑、侧翻，保证汽车的操纵稳定性与安全性[2]。

近年来，许多学者对线控制动系统的制动力分配策略进行了研究。黄源[3]首先根据各车轮的垂直载荷计算值对制动压力进行初始分配，然后根据各车轮轮速的差异调节制动压力。Xu等[4]根据制动强度的变化对前、后轴的制动力分配进行了自适应调节。Ding 等[5]使用滑模控制算法设计了横摆力矩控制器来确保质心侧偏角和横摆角速度尽可能接近各自的理想值。Sun等[6]基于径向基函数和粒子群优化算法设计了制动力分配策略。Ataei 等[7]使用模型预测控制方法设计了多目标集成控制器，可实现驱动和制动过程的滑移控制、横向稳定性控制、操纵性能改进以及防侧翻功能。Ji 等[8]利用自适应径向基函数网络可通过学习逼近任意非线性函数的特性，提出了一种新型的汽车动态稳定性控制策略。Ahmadian 等[9]采用主动转向控制和直接横摆力矩控制相结合的方法保证汽车制动稳定性。此外，也有部分学者[10-13]采用分层控制的方法，其上层控制器通常使用PID、滑模控制等算法来求取附加横摆力矩，下层控制器大多使用优化方法来分配附加横摆力矩。

与PID 算法相比，自抗扰控制（Active Disturbance Rejection Control，ADRC）算法解决了快速性和超调量的矛盾问题；与模糊控制、滑模控制等算法相比，ADRC算法方便实现、适用性广、不依赖于模型。

本文借鉴上述基于垂直载荷进行制动力分配和设计附加横摆力矩控制模块的思路，首先基于垂直载荷估计值进行制动力初始分配，再利用基于ADRC算法设计的附加横摆力矩控制模块求取提升车辆操纵稳定性的附加横摆力矩，最后通过制动力调节模块对初始分配的制动力进行调节，以提升汽车弯道制动时的制动效能和操纵稳定性，提高行车安全性。

2 数学模型

2.1 汽车弯道制动时的载荷转移

汽车弯道制动时，车轮的垂直载荷会发生转移，以汽车左转制动工况为例，4个车轮的垂直载荷分别为：

式中，FZ_L1、FZ_R1、FZ_L2、FZ_R2分别为左前轮、右前轮、左后轮、右后轮的垂直载荷；l1、l2分别为汽车质心与前、后轴的距离；g为重力加速度；ax、ay分别为汽车的纵向、侧向加速度；m为整车质量；L为轴距；w为质心高度；c为轮距。

2.2 二自由度汽车模型

在对汽车进行操纵稳定性研究时，通常选用横摆角速度和质心侧偏角作为评价指标，因此本文选择考虑沿y轴的侧向运动和绕z轴的横摆运动的二自由度汽车动力学模型作为参考模型，如图1所示。该模型忽略了转向系统、悬架系统等对汽车的影响，可以计算出横摆角速度和质心侧偏角的理想值，作为本文的评价基准。

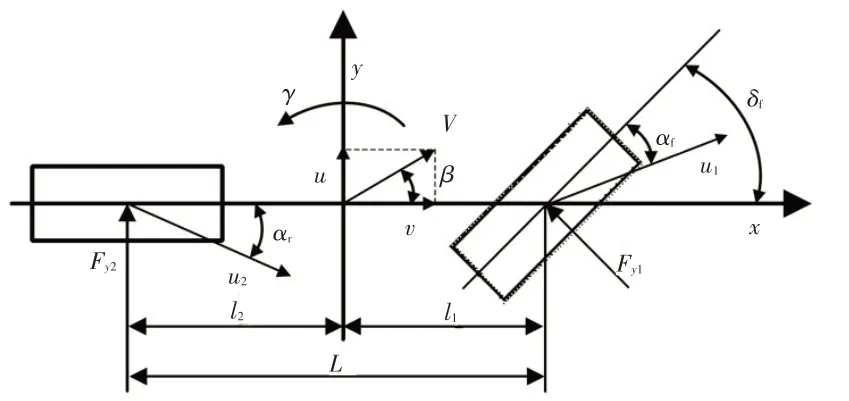
图1 二自由度汽车动力学模型

图1 中：δf为汽车前轮转角；u1、u2分别为前、后轮的实际运动速度；αf、αr分别为前、后轮的侧偏角；Fy1、Fy2分别为前、后轮的侧偏力；u、v分别为质心横向、纵向运动速度；V为质心的合成速度；β为质心侧偏角；γ为质心横摆角速度。

二自由度汽车动力学模型微分方程为：

式中，kf、kr分别为前、后轴侧偏刚度；IZ为汽车绕Z轴的转动惯量。

汽车稳态运行时横摆角速度γ、质心侧偏角β为定值，故可令和?为0，此外，汽车在转向过程中侧向加速度受到路面附着条件的限制，即ay=γv≤μg，得到理想横摆角速度为：

式中，μ为地面附着系数；sgn()为符号函数；K为汽车稳定性因数：

同理可得理想质心侧偏角为：

2.3 自抗扰控制算法

自抗扰控制算法主要包括跟踪微分器、扩张状态观测器和非线性状态误差反馈控制律，其基本结构如图2所示[14]。

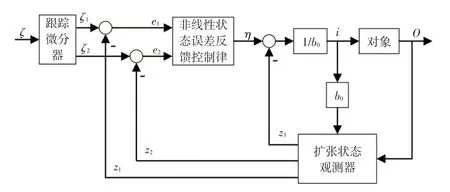
图2 ADRC基本结构

跟踪微分器可以从不连续或带噪声的输入信号中提取出跟踪信号及微分信号，简化控制器的设计并提升控制效果。跟踪微分器的离散形式为：

式中，ζ(k)为k时刻输入信号；ζ1(k)、ζ2(k)为k时刻从输入信号中提取的跟踪信号及微分信号；h为采样周期；ρ为速度因子；h0为fst()函数的步长；fst()为最速控制综合函数：

式中，x1、x2为fst()函数的2 个输入变量；d=ρh0；d0=h0d；y=x1+h0x2；a0=

扩张状态观测器用于解决ADRC 中扰动观测这一关键问题。它将总扰动扩张成系统的一个新状态变量，然后利用系统的输入、输出重构出包含系统原有状态变量与扰动的所有状态。离散形式的扩张状态观测器表示为：

式中，z1(k)、z2(k)为k时刻扩张状态观测器对系统的状态变量的估计；z3(k)为k时刻扩张状态观测器对系统的总扰动的估计；i(k)为k时刻被控对象的输入；o(k)为k时刻被控对象的输出；ε1为系统的状态变量估计z1(k)与被控对象的输出o(k)的差值；β01、β02、β03为增益系数；b0为控制系统的特征参数；σ为线性段的区间长度；fal()函数可表示为：

式中，e为fal()函数的输入变量；α为fal()函数的形状因子。

非线性状态误差反馈控制律既可以将跟踪微分器和扩张状态观测器输出的误差信号组合成类似PID 控制的线性组合，也可以利用fal()函数构造非线性控制组合，本文选择的PD形式的非线性组合为：

式中，η为非线性状态误差反馈控制律的输出；0<α1<1<α2；β1、β2为fal()函数的系数；e1、e2分别为跟踪微分器输出的跟踪信号及微分信号与扩张状态观测器的输出之差。

3 控制策略

3.1 整体方案

图3所示为控制策略的整体方案，其主要包含基于垂直载荷估计值的制动力初始分配模块、附加横摆力矩控制模块以及制动力调节模块。

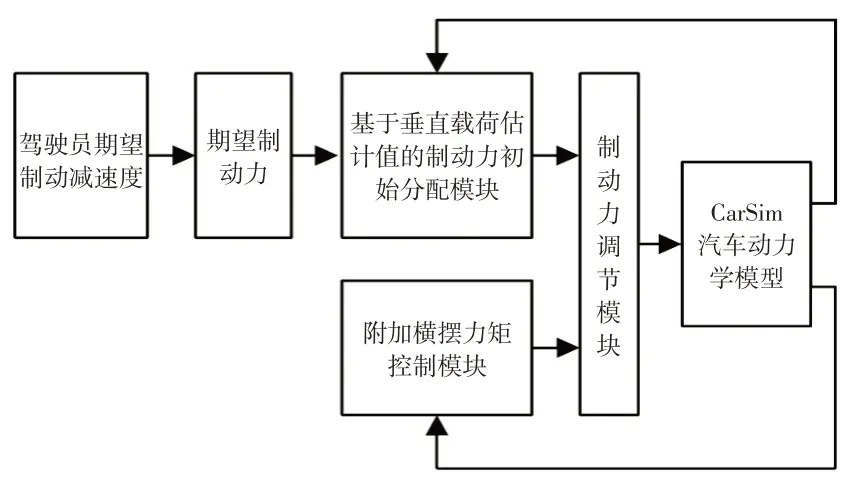
图3 整体方案

3.2 基于垂直载荷估计值的制动力初始分配模块

Limpert[15]提出了牵引系数这一概念，并将其定义为制动力与车轴垂直载荷的比值：

式中，μTj为第j轴的牵引系数；FXj为第j轴的制动力；FZj为第j轴的垂直载荷。

同时，Limpert还指出，汽车制动时的最优制动力分配策略应使前、后轴的牵引系数相同，这时前、后车轮可以同时达到附着极限。汽车进行弯道制动时，载荷会在前、后轴以及同一轴的左、右轮之间转移，这时4个车轮的垂直载荷各不相同，若要使4个车轮同时到达附着极限，则各车轮的牵引系数应满足：

式中，μT_L1、μT_R1、μT_L2、μT_R2分别为左前轮、右前轮、左后轮、右后轮的牵引系数。

式（12）等价于：

式中，FX_L1、FX_R1、FX_L2、FX_R2分别为左前轮、右前轮、左后轮、右后轮的制动力。

汽车制动时，首先根据驾驶员的期望减速度ad计算出汽车需要的制动力Fd，然后将Fd按照式（13）所示的比例关系分配给4个车轮：

根据式（15）进行汽车弯道制动力的初始分配，可以尽量使各车轮同时达到附着极限，从而显著提升汽车的制动效能。

3.3 附加横摆力矩控制模块

图4 所示为附加横摆力矩控制模块，其主要包含ADRC 横摆角速度控制模块和ADRC 质心侧偏角控制模块。ADRC 横摆角速度控制模块可以求取汽车实际横摆角速度γ跟随理想横摆角速度γd所需的附加横摆力矩ΔMγ；ADRC 质心侧偏角控制模块可以求取汽车实际质心侧偏角β跟随理想质心侧偏角βd所需的附加横摆力矩ΔMβ。汽车稳定性受到横摆角速度和质心侧偏角的共同影响，因此设置综合模块，其输出为：

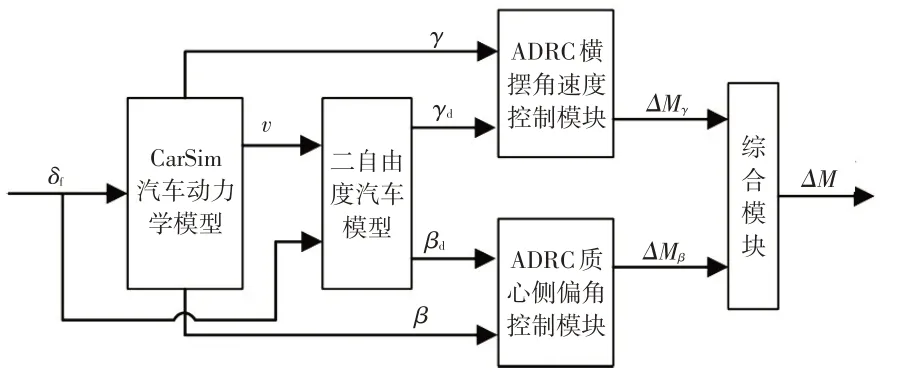
图4 附加横摆力矩控制模块

3.4 制动力调节模块

利用附加横摆力矩控制模块求取的附加横摆力矩ΔM需要转换成各车轮的附加制动力。附加制动力作用于不同的车轮会产生不同效果，以汽车左转工况为例，外侧车轮制动力增大时会产生负的横摆力矩，内侧车轮制动力增大时会产生正的横摆力矩。此外，当附加横摆力矩ΔM较大时，单独调节外侧车轮或内侧车轮的制动力可能会导致其快速到达路面纵向附着极限，进而产生抱死现象。因此，本文选择同时调节外侧车轮和内侧车轮的制动力来施加附加横摆力矩ΔM。

同样以汽车左转工况为例，为简化计算，忽略前轮转角的影响，首先计算ΔM对应的制动力ΔF，然后将ΔF按照各轮垂直载荷的比例关系分配给4个车轮：

式中，ΔFX_L1、ΔFX_R1、ΔFX_L2、ΔFX_R2分别为左前轮、右前轮、左后轮、右后轮的附加制动力，则各车轮的制动力修正为：

4 仿真分析

利用Simulink/CarSim 联合仿真验证制动力控制策略的有效性，CarSim整车动力学模型的部分参数如表1所示。

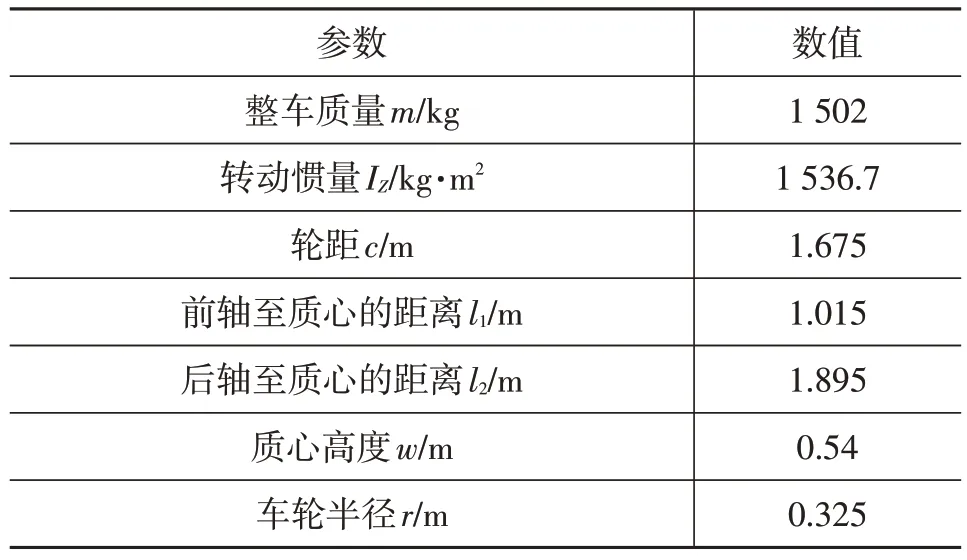
表1 CarSim整车动力学模型参数

为了进一步验证本文设计的分配策略（优化分配方案）的有效性，将该分配方案与比例分配方案的结果进行对比。当制动主缸输入压力为P时，比例分配方案中，各车轮的制动压力为：

式中，PL1、PR1、PL2、PR2分别为比例分配方案中左前轮、右前轮、左后轮、右后轮的制动压力。

为模拟汽车在高速转弯过程中的制动工况，设置仿真工况如下：车辆以v=80 km/h 的初速度在路面附着系数μ=0.85 的干沥青路面上行驶，前轮转角输入为1.5°，制动减速度分别为0.3g、0.5g和0.7g，汽车在第0 s 时开始制动，在1 s 内制动减速度线性增大到最大值后保持不变。

4.1 轮速响应

图5 所示为采用比例分配方案时不同制动减速度条件下的轮速响应曲线。当制动减速度较小（0.3g）时，由于汽车垂直载荷转移程度较弱，各车轮的轮速近似相等，未发生抱死现象；当制动减速度为0.5g时，随着垂直载荷转移程度的增强，分配给内后轮的制动力大于地面所能为其提供的最大纵向力，导致内后轮在第1.6 s时完全抱死；当制动减速度为0.7g时，由于垂直载荷转移程度的进一步加剧，除内后轮在第1.2 s 时完全抱死外，内前轮也在制动过程中出现了轻微的抱死现象。由图5可知，由于比例分配方案在弯道制动过程中无法针对垂直载荷的转移动态调整4个车轮的制动力，导致制动减速度较大时部分车轮出现抱死现象，降低了汽车的制动效能。

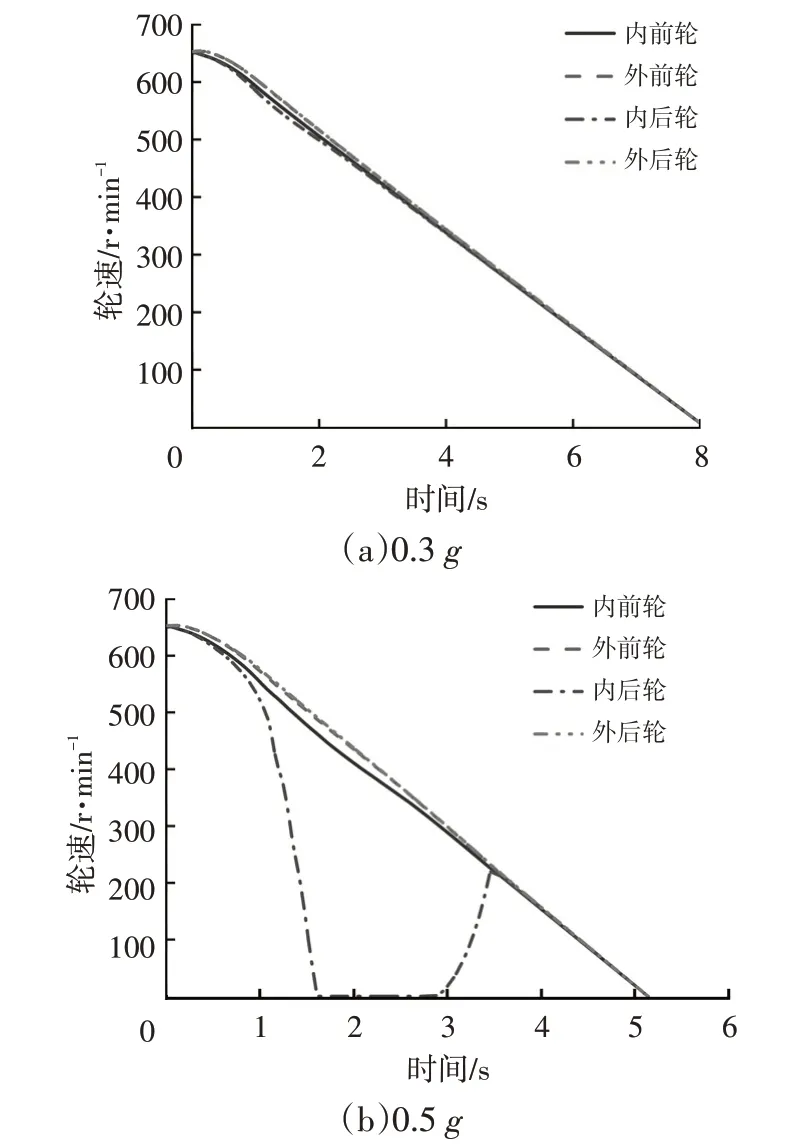
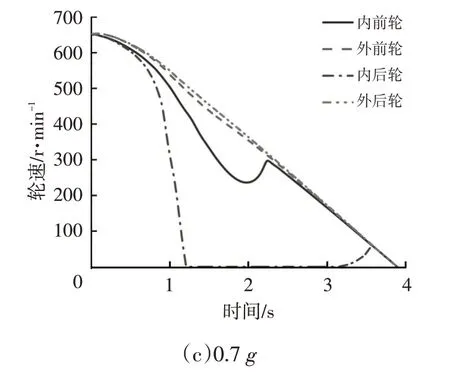
图5 采用比例分配方案时不同制动减速度下的轮速响应

图6 所示为采用优化分配方案时不同制动减速度下的轮速响应曲线。由于本文提出的制动力分配策略可以针对汽车各车轮垂直载荷的变化动态调整各车轮的制动力，能够充分利用地面附着力，使得汽车在弯道制动过程中基本无抱死现象，在提高制动效能的同时极大地提升了行车安全性。

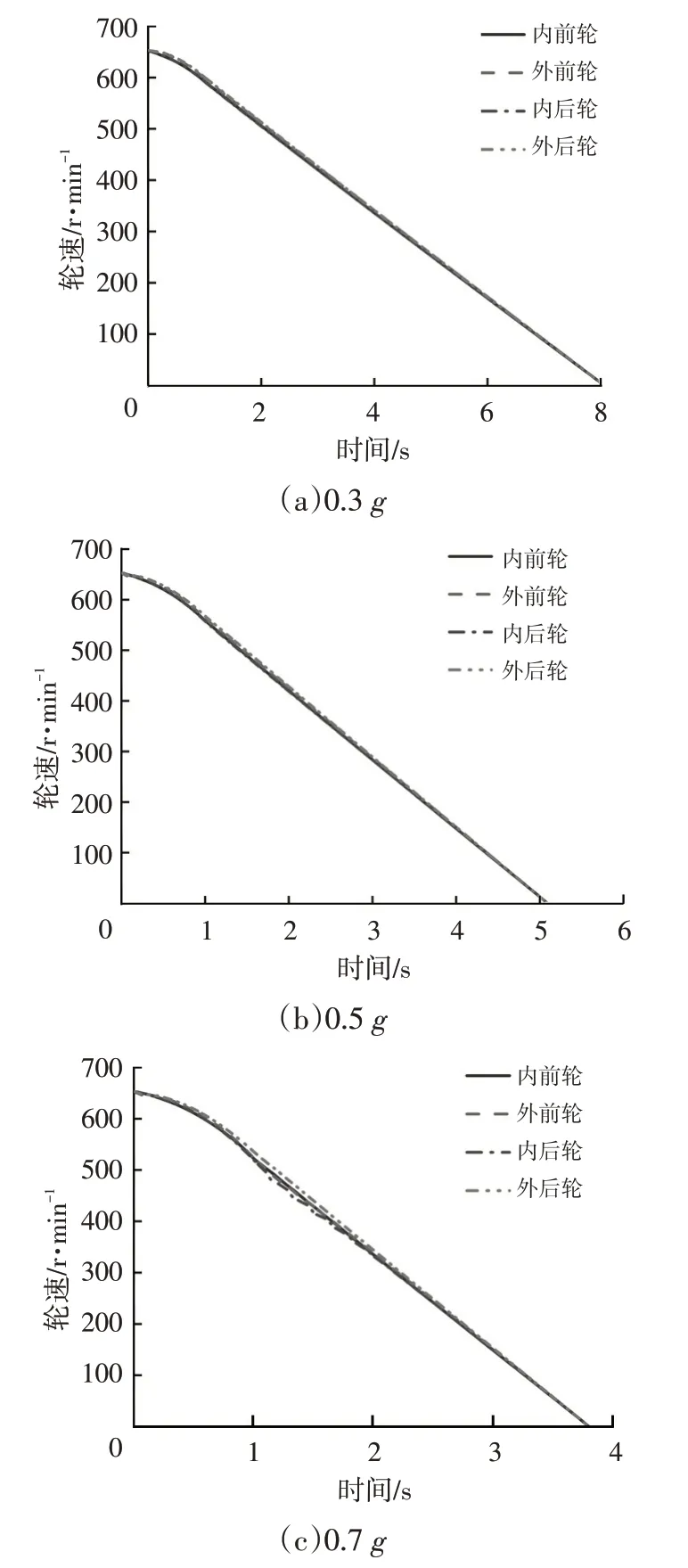
图6 采用优化分配方案时不同制动减速度下的轮速响应

4.2 横摆角速度响应

图7 所示为采用比例分配方案和优化分配方案时不同制动减速度下的横摆角速度响应。由图7可知，在不同的制动减速度下优化分配方案的横摆角速度较比例分配方案都更加接近于理想横摆角速度，能够更好地满足汽车弯道制动时的操纵稳定性需求。

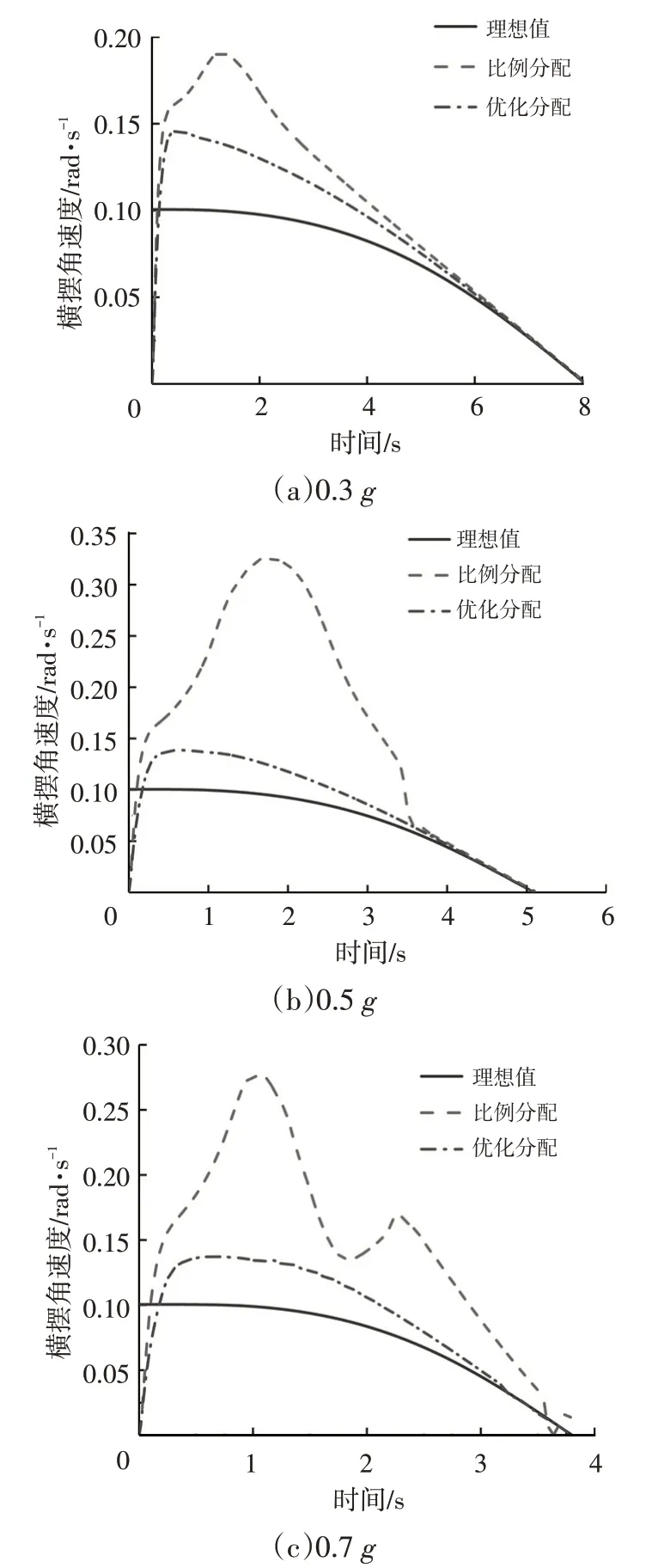
图7 不同制动减速度下的横摆角速度响应

4.3 质心侧偏角响应

图8 所示为采用比例分配方案和优化分配方案时不同制动减速度下的质心侧偏角响应。由图8可知，在不同制动减速度下优化分配方案的质心侧偏角较比例分配方案都更加接近于理想质心侧偏角，提升了汽车弯道制动时的操纵稳定性。

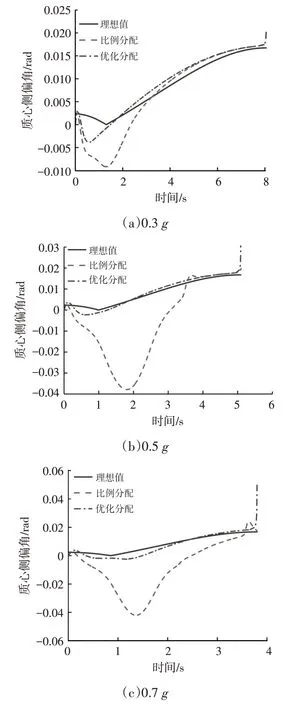
图8 不同制动减速度下的质心侧偏角响应

4.4 优化分配方案制动力分配结果

图9 所示为不同制动减速度下优化分配方案的制动力分配结果。受汽车自身的轴荷分配及弯道制动过程中的载荷转移影响，前轴的垂直载荷大于后轴垂直载荷，同时同一轴外侧车轮的垂直载荷大于内侧车轮垂直载荷，因此优化分配方案分配给前轴车轮的制动力较后轴车轮大，同时分配给同一轴的外侧车轮的制动力较内侧车轮大。

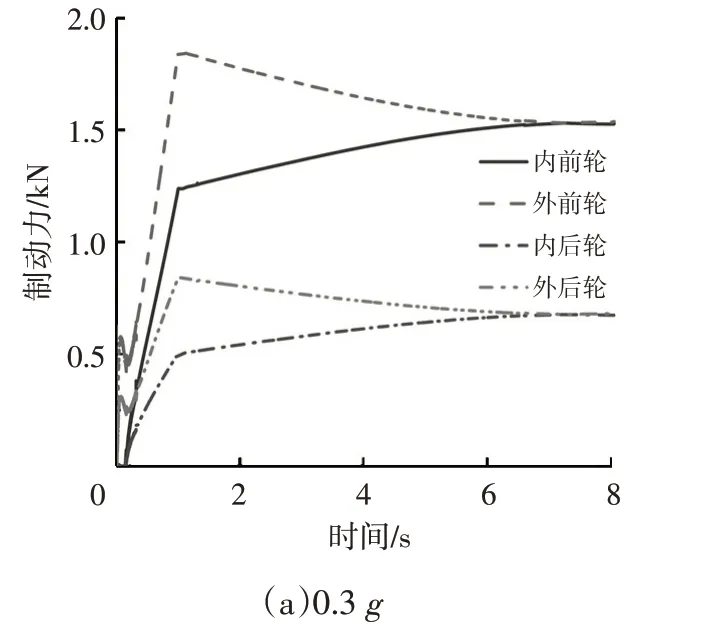
图9 不同制动减速度下优化分配方案制动力分配结果

5 结束语

本文提出了一种新型汽车弯道制动力控制策略，首先根据驾驶员的期望减速度得到所需的制动力，基于垂直载荷估计值进行制动力初始分配，其次，利用基于ADRC 算法设计的附加横摆力矩控制模块求取提升操纵稳定性所需的附加横摆力矩，最后通过制动力调节模块对初始分配的制动力进行调节。采用Simulink 与CarSim进行联合仿真，并在不同制动减速度工况下与比例分配方案的轮速、横摆角速度以及质心侧偏角响应进行了对比。结果表明：当制动减速度较大时，采用比例分配方案时部分车轮会出现抱死现象，降低了制动效能，而本文提出的制动力控制策略可以随着垂直载荷的转移动态调整各车轮的制动力，避免了车轮抱死现象，提高了制动效能；本文提出的制动力控制策略在不同的制动减速度下，汽车的横摆角速度和质心侧偏角都更加接近各自的理想值，显著提高了弯道制动时的操纵稳定性，保障了弯道制动的安全性。