基于回旋曲线的垂直泊车路径规划

张明海 丁宁 曹立波 颜京才 李旭升

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082；2.毫末智行科技有限公司保定分公司，保定 071000）

主题词：自动泊车 路径规划 直线—圆弧—回旋曲线

1 前言

随着汽车保有量的不断增加，城市交通严重拥堵，泊车环境越来越拥挤、复杂，技术不足或缺乏经验的驾驶员难以将车辆安全、准确、快速地泊入车位。因此，开发安全舒适的自动泊车系统对泊车安全具有重要意义[1]。

作为自动泊车系统的组成部分，路径规划模块是确保泊车过程安全舒适的关键[2]。曲线插值是常用的泊车路径规划方法，能够将路径用函数表达，具有运算耗时短、规划路径基本平滑可控的优点，缺点是缺乏灵活性。直线和圆弧组合是一种经典的方法，杜宾斯（Dubins）曲线[3]和Reeds-Shepp 曲线[4]可以生成两点间的最短路径，包括直线段和圆弧段，前者对应无倒车的情况，后者对应有倒车的情况。一些学者在此基础上进行了拓展或改进：Kim等[5]提出通过组合不同的圆弧和直线在狭窄环境中搜索所有可行路径，该方法较实用，且停车路径可以通过最小化成本函数进行优化；Sung⁃woo 等[6]将圆弧定位法应用于平行停车，提出了一种完全基于几何的方法，该方法最大的缺点是在直线和圆弧的连接点处曲率不连续，为了精确地跟踪路径，车辆必须在连接点停下，重新调整前轮方向，这将导致不必要的时间消耗和转向系统磨损。为了避免这些问题，学者们提出了一些解决方法，其中回旋曲线在处理路径平滑性方面具有独特优势。Vorobieva等[7-8]采用双圆弧规划平行泊车路径，然后使用回旋曲线进行平滑处理，解决了泊车过程中原地转向的问题。张家旭等[9]基于直线-圆弧组合方式设计平行泊车路径，并通过对固定回旋曲线的平移和翻转变换完成曲率连续的平行泊车路径规划，但使用回旋线时移动了圆弧端点。

本文采用几何方法，结合曲线路径最短和回旋曲线曲率平滑且符合车辆转弯特性的优点，对垂直车位的自动泊车路径规划开展研究。考虑开始泊车时航向角不为零的情况，首先使用直线圆弧组合的方式设计基础的一步和多步泊车路径，然后使用回旋线对圆弧段进行优化，可以有效消除路径中曲率突变的不平滑点，使整个泊车路径曲率连续，避免原地转向，以实现不同初始位置和姿态角条件下的垂直泊车路径规划。

2 垂直泊车基础路径规划

2.1 汽车运动学模型

为保证泊车过程的准确性，需要对车身轮廓运动轨迹进行计算，在给予一定裕度的情况下，将车身轮廓等效为矩形，如图1所示，图中L为轴距，Lf、Lr分别为前、后悬，W为车宽。

图1 汽车简化模型

由于泊车过程车速较低，可以忽略车辆侧倾和轮胎滑移的情况。本文采用基于阿克曼转向原理的运动学模型，将车视为平面刚体，选取后轴中心作为参考点，具有x、y、φ3个自由度，其中(x,y)为车辆坐标，φ为航向角，是车身与x轴正方向的夹角，逆时针为正，如图2所示。

图2 阿克曼转向模型

车辆的状态方程为：

式中，v为车速；δ为等效前轮转角。

根据最大等效前轮转角δmax和轴距L，可求得后轴中心对应的最小转弯半径Rmin：

2.2 单步泊车路径规划

车辆开始泊车时，首先通过全景环视系统检测车位角点P1、P4，在车位左角点P1处建立坐标系。此时后轴中心位于S1点，以S1为规划起点，坐标可根据P1、P4点得到，车身与车位的夹角φ即为初始航向角，垂直停车位尺寸为l×w，如图3 所示。车辆先从S1点沿X轴前进或后退至S2点，再按最小转弯半径Rmin行驶至S3点，切换倒挡按Rmin后退至S4点，最后沿直线后退至S5点泊入车位。图3中曲线为车辆后轴中心的轨迹，O0为的圆心，对应的圆心角为θ0，O1为的圆心，对应的圆心角为θ1。

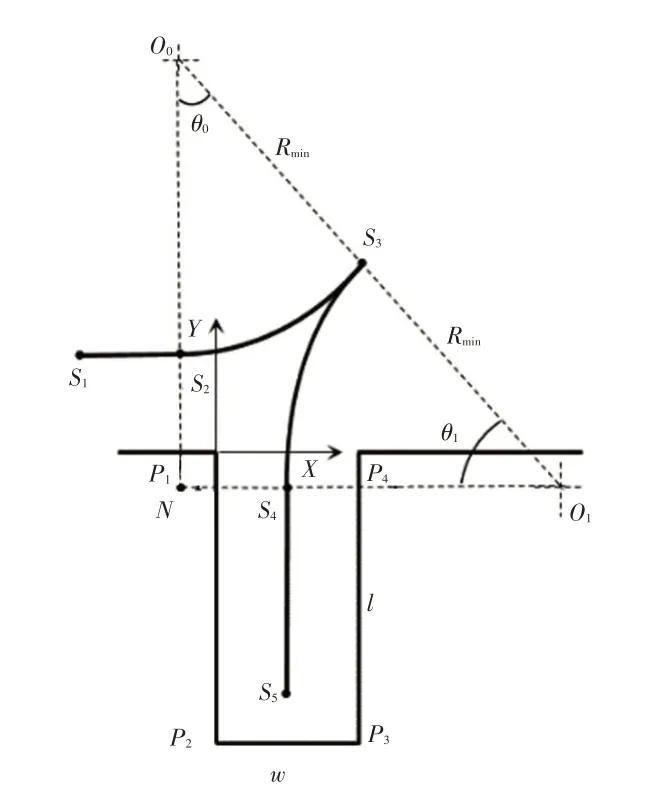
图3 单步垂直泊车示意

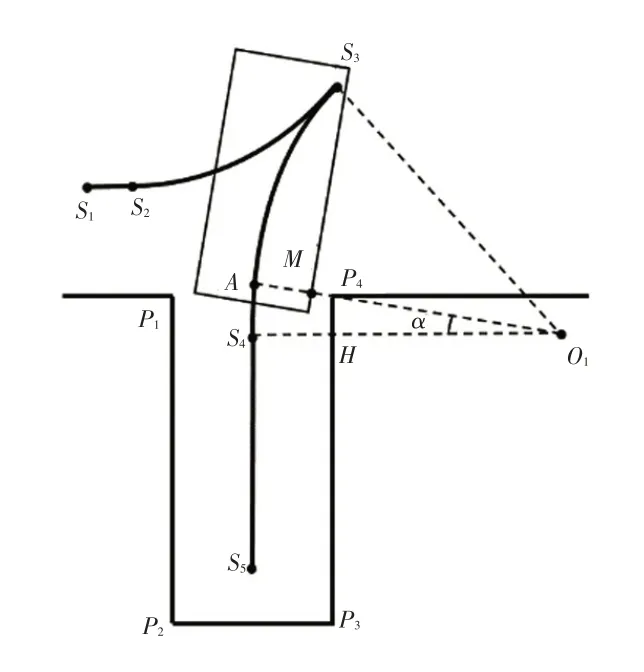
图4 单步泊车碰撞风险点示意

由图4中几何关系可得O1的坐标为：

图3中O0的Y坐标为：

在图3中，对于ΔO0O1N，有：

由此可得O0的X坐标为：

S2、S3、S4的坐标可以通过式（4）～（7）求得：

实际泊车时，起始点可能相对于S2点偏前，须先后退一段距离，如图5所示。此外，初始航向角φ一般不为0°，泊车过程需先通过一段圆弧，将车辆调整到与X轴平行的位置，再按照以上方法进行泊车，图6 所示为初始航向角不为零的泊车路径。

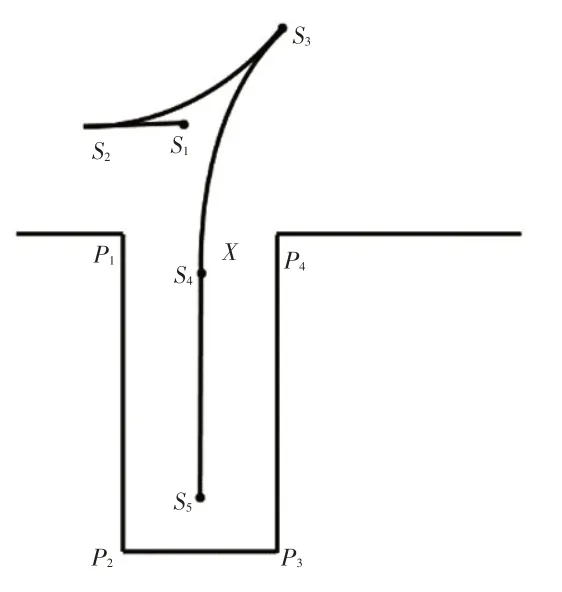
图5 起始点偏右时泊车路径示意

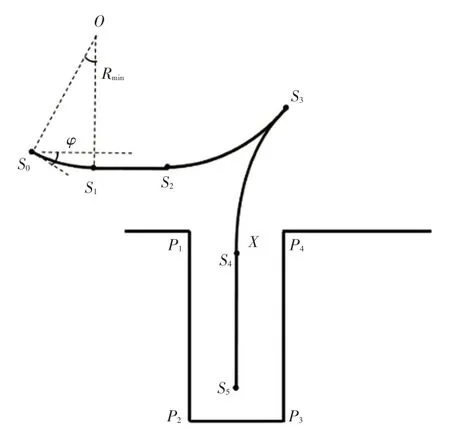
图6 初始角度φ≠0°的泊车路径示意

2.3 多步泊车路径规划

单步泊车所需空间较大，垂直泊车场景常遇到泊车空间不足的情况，比如道路较窄或对向车位停有车辆。如图7 所示，车辆轮廓左前点A1与上边界会发生碰撞。此时单步泊车难以实现，需采用多步泊车的方法完成。从图7中可以看出，引起碰撞的原因是一步泊车路径中S3点的Y坐标过大，因此，通过约束YS3即可避免碰撞。

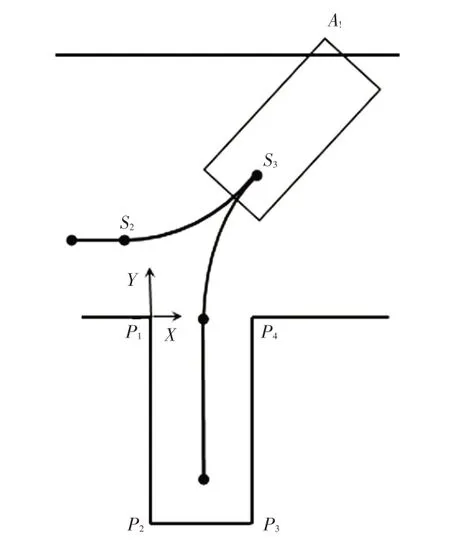
图7 车辆与上边界碰撞示意

图8 为车辆在S3点以及行驶至A点的泊车示意，为避免碰撞，车辆左前点A1与上边界需保留安全距离，将J与A1的距离定为安全距离Lsafe2。

图8 多步垂直泊车空间约束

由图8中几何关系可得：

由图9和图10中几何关系有：

图9 多步泊车路径示意

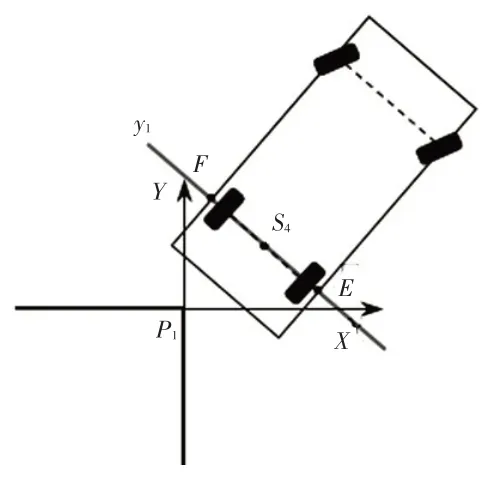
图10 S4点计算示意

设直线EF的解析式为y1=kx+b，则：

由式（19）～（22）可得到θ2、θ3的值以及O2、O3、S5、S6的坐标。

3 垂直泊车路径规划算法优化

前文设计的路径规划方法由直线和圆弧组成，可以完成泊车任务。但由于曲率不连续，要使车辆沿规划的路径行驶，必须在直线和圆弧连接处停车原地转向，这会造成转向机构及轮胎的磨损，还会延长泊车时间。因此，需要对第2节中的路径进行优化。回旋曲线可以很好地描述车辆行驶时转向的行为，如果车辆以恒定的速度运动，并以恒定的角速度转向，则后轴中心驶过的轨迹即为回旋线。回旋线具有曲率连续变化的特点[10]，满足泊车路径对曲率平滑的要求。本文使用回旋曲线对基础路径进行优化。

3.1 回旋曲线

回旋曲线是曲率K随其弧长s线性变化的曲线，可表示为：

式中，σ为曲率变化率。

车辆从起点O开始，初始状态为q0=(x0，y0，φ0，δ0)=(0，0，0，0)，x0、y0、φ0、δ0分别为车辆的初始x坐标、y坐标、车身航向角、曲率，以恒定的纵向速度和恒定的转向速度向左行驶，直至点E，转向盘到达最大角度，此时转弯半径为Rmin，车辆后轴中心驶过的轨迹如图11所示。距起始点s处车辆的姿态信息为：

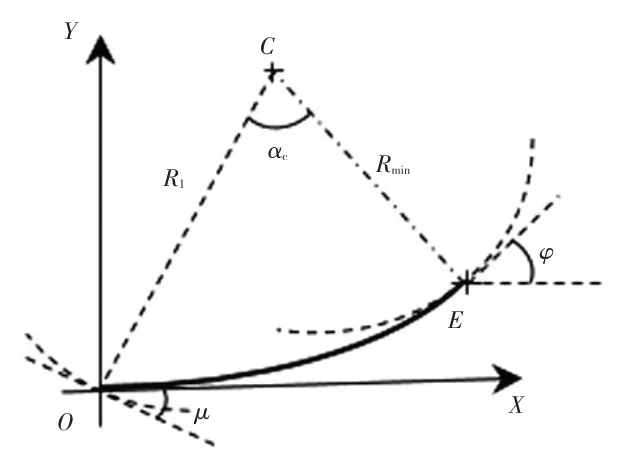
图11 回旋曲线

式中，A为回旋曲线参数，A2=RL=1/σ；Cf、Sf为菲涅尔积分：

圆心C的坐标为：

由图11可得：

为充分利用车辆的最大转向角并缩小泊车空间，回旋曲线长度S应尽可能小。回旋曲线长度与车速及转向速度有关：

式中，tmin为转向盘从0°转到最大角度所需时间；vδ为最大转向速度；vmax为泊车过程中的最大车速。

所用回旋线参数定为A2min=RminSmin，R1由式（25）～式（28）计算，αc为回旋线对应的角度。

3.2 连续曲率路径优化

第2节规划的路径中，存在的问题是直线与圆弧处曲率突变（从0 突变到1/R），且圆弧段起始曲率为1/R，这会给泊车过程带来困难。希望车辆每次前进/后退的路径曲率都是从0开始，并以0结束，且每一段路径曲率都是连续的。优化的思路是结合回旋线，将每一段圆弧都调整为“回旋线-圆弧-回旋线”（CAC）组合的曲线。

定义CAC 组合曲线包括：参数为A的回旋线，长度S，初始曲率为0，末端曲率为1/R；半径为R，角度为θ的圆弧；参数为A的回旋线，长度L，初始曲率为1/R，末端曲率为0。

针对第2节的结果，将最小半径Rmin替换为R1，使用回旋曲线将半径为R1的圆弧过渡到半径为Rmin的圆弧。此外，需将圆弧以S2为中心旋转角度μ，从而使优化后的航向角连续，如图12所示。

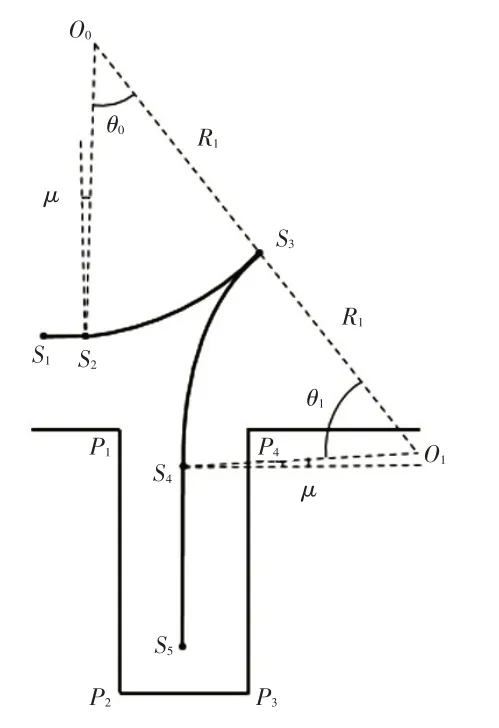
图12 回旋曲线优化的泊车路径示意

对于不同的圆心角度α，转化为回旋曲线-圆弧-回旋曲线（CAC 序列），考虑以下2 种情况：当α≥2αc时，使用完整的CAC 序列，如图13a 所示；当α<2αc时，使用2段回旋线（CC 序列）进行优化，如图13b 所示。回旋线对应的参数Anew、Lnew将有所变化：

图13 回旋曲线优化圆弧的2种情况

式中，Δφ=(φend-φstart)为汽车转过的角度。

4 仿真验证

本文针对某品牌SUV 汽车展开试验，汽车相关参数如表1 所示，采用尺寸为2.5 m×6 m 的垂直车位。通过MATLAB对垂直泊车进行仿真。

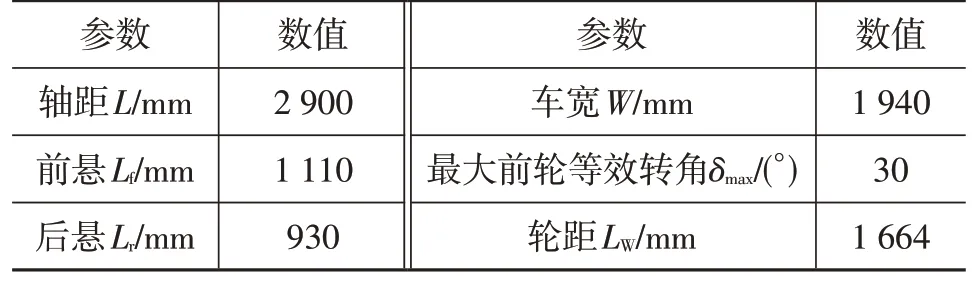
表1 汽车主要参数

图14 所示为汽车单步泊车规划的路径，图14a中，车辆的初始坐标为(-2,2)，初始航向角为0°；图14b中，初始坐标为(-3,2)，初始航向角为-5°。对于不同的初始位置和角度，本文的方法可以规划出直线-圆弧-回旋曲线组合的安全平滑泊车路径，但所需泊车空间较大。

图14 单步泊车仿真结果

为确保泊车过程的安全性并提高路径规划的适用性，根据实际泊车场景，将横向泊车距离限制为6 m。图15 为在不同的初始坐标和初始航向角下，规划的多步泊车路径均能避免碰撞且平滑。

图15 多步泊车仿真结果

5 结束语

本文对垂直车位自动泊车场景，规划了具有不同初始航向角的平滑泊车路径。首先，根据车辆初始姿态以及泊车空间，考虑运动学约束和碰撞约束，设计基于直线-圆弧组合的单步和多步垂直泊车基础路径规划方法。然后，对于连接点曲率不平滑的问题，结合回旋曲线对基础路径规划结果进行优化，实现了泊车路径的曲率平滑，有效避免了泊车过程中的原地转向。基于MATLAB 的仿真结果表明，对于不同的初始航向角，该方法能规划出安全无碰撞的平滑轨迹，验证了安全性和可行性。