基于VMD 样本熵和改进极限学习机的滚动轴承故障诊断
封成东,李玥,封成智
(1. 甘肃农业大学信息科学技术学院,甘肃 兰州 730000;2. 甘肃省生产力促进中心,甘肃 兰州 730000)
随着工业现代化进程的推进,旋转机械设备趋向高可靠性、高精度、低故障率发展,滚动轴承作为旋转机械设备的重要元件,其工作稳定性对设备安全可靠运行有重要影响。如何在滚动轴承的生命周期内准确、快速的识别轴承的局部或者早期故障并进行预防性维修是设备管理的重要内容,也是降低维修和运行成本、提高设备运转率的必然要求。
当滚动轴承出现损伤缺陷甚至局部失效时,其运行过程中产生的振动信号必然会发生变化,振动信号呈现出非线性、非平稳性特征[1]。在实际工程应用中,通过监测旋转设备的运行工况,采集滚动轴承的振动信号数据,利用信号处理工具深入挖掘振动数据中蕴含的时频等状态信息,并提取有效的信息特征是实现滚动轴承故障诊断的有效方法。变分模态分解(VMD)是由Dragomiretskiy[2]等提出的解析信号时频特性的方法,该算法在求解变分问题的过程中能够实现频域的自适应划分,将信号划分为指定个数的调幅调频的模态分量,同时确定不同模态分量的中心频率和带宽[3],有效的避免虚假分量的产生,广泛应用于复杂的、非平稳信号的处理和故障模式识别领域。向玲等[4]采用VMD 算法对滚动轴承信号进行分解、模态分量的筛选和重构,分析重构信号的Teager能量谱并提取轴承故障特征频率,仿真结果验证了基于VMD和Teager能量谱故障识别模型的有效性,而且要优于EEMD 算法。蔡赛男等[5]提取了VMD 分解后各模态分量的多尺度排列熵作为滚动轴承的故障特征,并将故障特征样本导入鲸鱼算法优化最小二乘支持向量机的分类模型,取得了较好的诊断准确率。常勇等[6]提出了基于VMD和优化模糊聚类相结合的轴承故障识别算法,通过VMD和奇异值分解对信号进行去噪声和异常值,并采用粒子群优化的模糊聚类进行不同故障类型的准确识别。VMD 对滚动轴承的故障振动信号进行分解后会产生指定个数的模态分量,为了量化模态分量中包含的故障信息,引入样本熵来提取特征信息作为故障诊断依据。样本熵是在近似熵理论基础上的一种改进算法,通过计算信号中产生新模式的概率大小来度量时间序列的复杂性[7],样本熵的数值的大小直接反应时间序列的复杂性。
当滚动轴承的故障特征提取后,需要构建分类器对故障特征样本进行训练学习和识别。极限学习机(extreme learning machine,ELM)是基于前馈神经网络的学习算法,具有训练学习速率高、泛化性能强、应用领域广的优良特性[8-9]。在实际应用中,ELM 算法输入层与隐含层间的连接权值及隐含层神经元的阈值是随机初始化的,在运行过程中可能出现不稳定性、鲁棒性差的缺点[10]。本文引入群智能算法中的麻雀搜索算法(sparrow search algorithm,SSA)[11]来优化ELM的初始权值和阈值,并搭建基于改进SSA优化ELM的分类器模型,将提取的滚动轴承故障特征样本导入分类器进行故障类型的识别。
1 基本原理
1.1 VMD原理
VMD 的分解是在迭代运算中求解约束变分问题最优解的过程,假设一组非线性、非平稳信号y(t)被分解为一系列调幅调频的分量信号uk(t),k=1,2,…,K,公式如下:
式中:Ak(t)为幅值φk(t)为相位,wk(t) =φ'k(t)为瞬时频率。
VMD约束变分问题可表述为:对分解后的每个模态分量进行希尔伯特变换得到解析频谱,在频谱中加入预估的中心频率并将混合频谱调制到对应的基带,计算调制后基带的梯度平方范数得到各模态的频率带宽,各模态的频率带宽和为最小,约束变分问题的公式如下:
式中:∂t表示偏导,*为卷积,δ为Dirac 分布,变分问题的约束条件为各模态分量之和为原始信号。
引入Lagrange 乘法算子和二次惩罚系数,将约束变分的求解转化为求解非约束变分的过程[3],公式如下:
式中:L为增广拉格朗日函数,λ为Lagrange 乘法算子,α为二次惩罚系数。
对公式(3)采用乘法算子交替方向法和傅里叶等距变换,迭代更新μk和wk得到模态分量和中心频率,具体公式如下:
本文结合VMD 中心频率法和模态分量的频率混叠性来确定VMD的分解个数,以美国Case Western Reserve University 实验室提供的滚动轴承振动数据为研究对象,振动数据是通过加速度传感器采集。这里以一组滚动轴承内圈故障信号为例,电机负载为735W,采样频率为12 000Hz,采样时间为0.2 s,采样长度为2 400,损伤直径为0.177 8mm,信号波形如图1 所示。采用VMD 分别对内圈故障信号进行2、3、4、5层分解,得到各模态分量的中心频率分布。分析表1可知,当分解层数为5时,模态4和模态5的中心频率比较接近,此时画出信号的4层分解和5层分解图以及对应的快速傅里叶变换后频谱图,如图2~3所示。由图3可知,分解层数为5时,模态4和模态5出现了频率混叠性,而4层分解后各模态分量并没有频率混叠现象,因而对内圈故障信号进行VMD分解的层数为4,同理轴承的正常、滚动体故障和外圈故障的VMD 分解层数通过分析均确定为4。
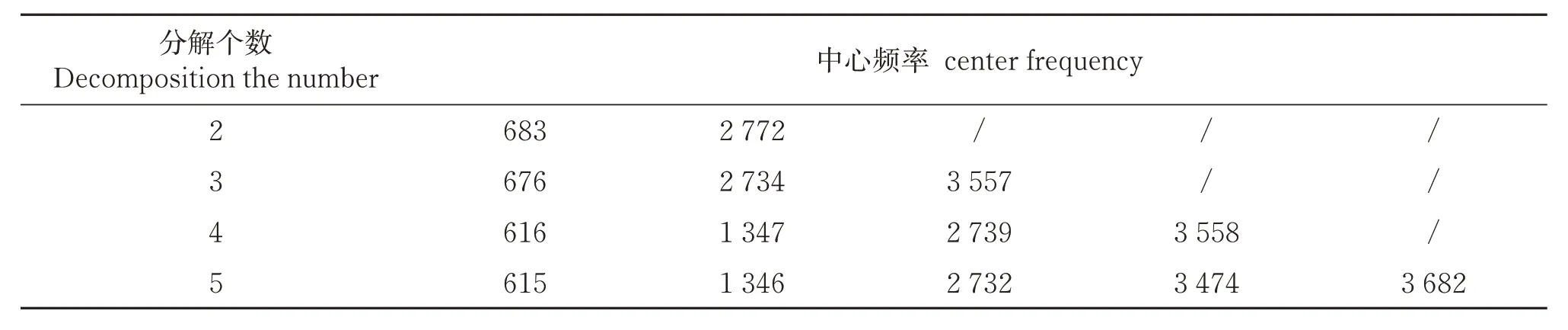
表1 VMD不同分解个数各模态的中心频率分布Table 1 Central frequency distribution of various modes of different decomposition numbers of VMD

图1 滚动轴承内圈故障波形图Figure 1 Rolling bearing inner race fault waveform
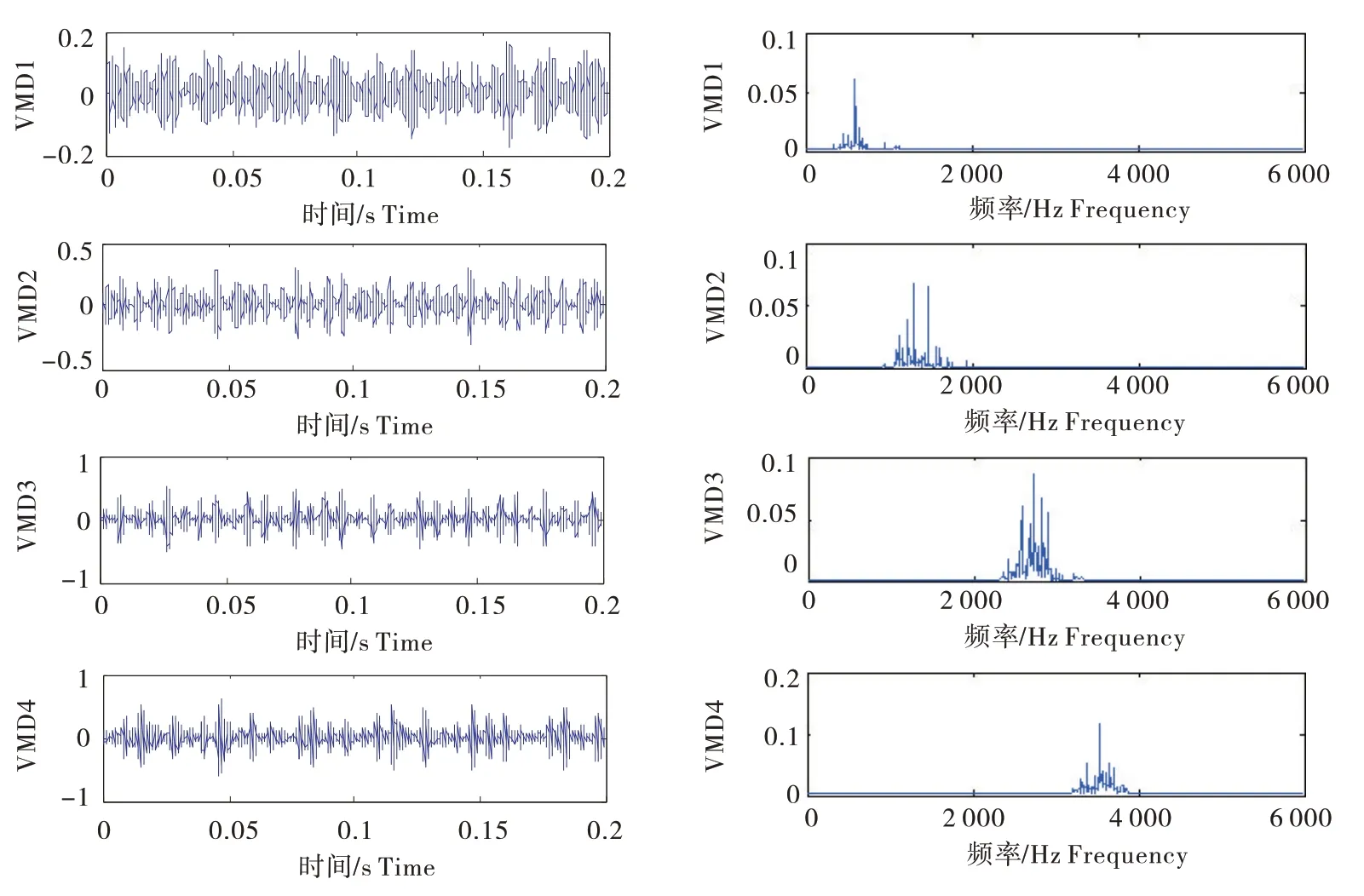
图2 内圈故障信号VMD四层分解波形图及频谱图Figure 2 VMD four-layer decomposition waveform and spectrum of inner race fault signal
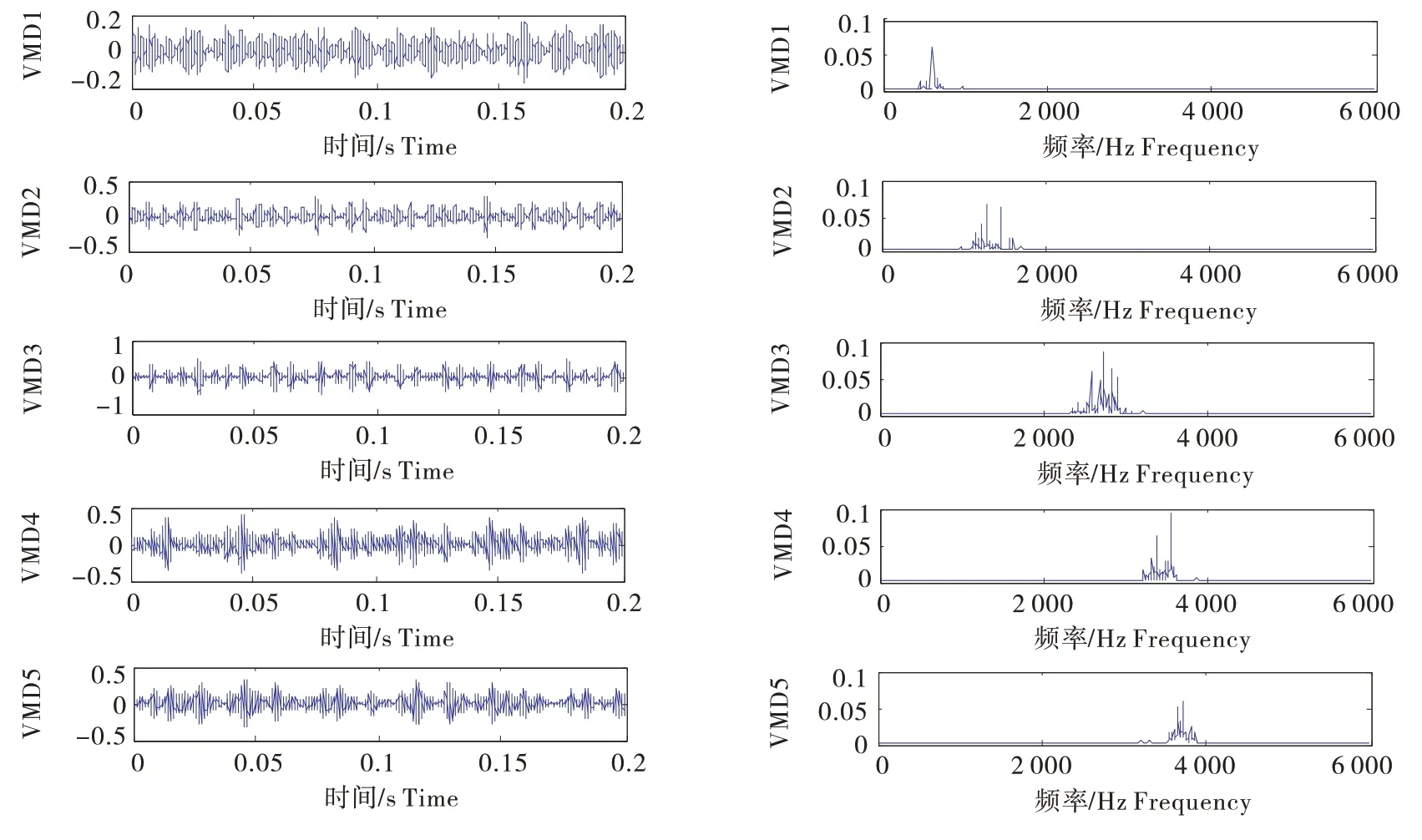
图3 内圈故障信号VMD五层分解波形图及频谱图Figure 3 Five-layer decomposition waveform and spectrum of VMD of inner race fault signal
1.2 样本熵
在实际应用中,样本熵的大小能度量数据序列的自我相似性和复杂性,而且样本熵的计算不依赖于信号的数据长度,因而在量化滚动轴承故障信号的特征时具有更好的统计稳定性和适应性,样本熵的计算步骤如下[12]:
(1) 给定原始时间序列x={x1,x2,…,xN},选择合适的嵌入维数m构造新的状态向量,x={xi,xi+1,…,xi+m-1},i=1,2,…,N-m。
(3) 给定相似性容限参数r,统计xi和xj之间的距离小于等于r的数量Bi,并做如下定义:
(4) 计算(r)的平均值:
(5) 将嵌入维数增加为m+1,重复上述4个步骤并计算得到Bm+1(r),当时间序列的长度为有限值时,样本熵计算为如下公式:
选取轴承的正常、内圈故障、滚动体故障和外圈故障振动信号,电机负载为735 W,采样频率为12 000Hz,采样时间为0.2 s,采样长度为2 400,故障损伤直径为0.177 8 mm,分别对4 种信号进行4 层VMD 分解,并提取各模态分量的样本熵,见图4,通过提取样本熵构建滚动轴承的特征样本并作为分类识别的依据。

图4 VMD分解后各模态的样本熵Figure 4 Sample entropy of each mode after VMD decomposition
1.3 极限学习机
相对于传统的前馈神经网络,极限学习机(ELM)的网络结构简单,只需要设定隐含层神经元数量、输入层神经元和隐含层神经元之间的连接权值以及隐含层神经元的阈值,其他层间的连接权值和阈值不需要调整,因而ELM 的网络学习、训练运算效率有明显的提升[13-14]。
假设给定的样本为(xi,yi),1 ≤i≤N,且均为实数范围内,ELM网络模型可表示为如下:
式中:Yj是网络输出,L为隐含层神经元个数,wi为输入层神经元和第i个隐含层神经元的连接权值,bi为第i个隐含层神经元的阈值,φ为激活函数,βi为第i个隐含层神经元与输出层神经元的连接权值。
ELM 的训练目标就是通过寻找最优的权值和阈值等参数,使得期望输出和网络输出的误差损失函数值最小,并得到最优解。
由于ELM 的输入层神经元和隐含层神经元之间的连接权值以及隐含层神经元的阈值是在网络结构中随机初始化的,实际应用中可能会出现过拟合、预测或者分类结果不稳定的病态现象[15],因为本文引入仿生智能优化算法对ELM进行优化,提高滚动轴承的故障诊断准确率。
2 基于改进麻雀搜索算法优化ELM的诊断模型
2.1 麻雀搜索算法基本理论
麻雀搜索算法(SSA)是2020 年提出的新型仿生智能算法,麻雀种群行为包括觅食和反捕食行为,觅食行为通过麻雀种群中的发现者和加入者实现,反捕食行为通过侦查预警机制实现[16-17]。SSA在解空间中具有优良的寻优搜索能力和快速收敛性能。
假设麻雀的种群规模为N,种群个体搜索最优解的空间维度为D,种群的集合向量为X={Xi},i=1,2,…,N,麻雀个体表示为Xi=[xi1,xi2,…,xid,…,xiD]。麻雀发现者的位置更新公式如下:
式中:xbt+1d表示麻雀个体在搜索空间第d维的最佳位置,xwtd表示麻雀个体在搜索空间第d维的最差位置,A表示长度为d、元素为-1或者1的向量。
麻雀种群在实现觅食行为时,会从种群中选择10%-20%的个体执行侦查预警机制,保证种群的安全,位置更新公式如下:
式中:β为个体移动步长控制系数,该系数是方差为1、均值为0的正态分布随机数,k为[-1,1]内的均匀随机数,fi为个体适应度,fg为当前迭代过程中种群最佳适应度值,fw为种群最差适应度值,e为防止分母为0的极小数值。
2.2 麻雀搜索算法的改进
虽然SSA 具有收敛速度快、局部寻优能力强的优点,但在迭代后期种群个体跳出局部极值的能力较弱,寻优过程中易陷于局部最优的缺点,因而为提高SSA的全局搜索能力对SSA进行改进,改进策略如下:
(1) 混沌初始化种群
标准SSA在种群初始化时,只是通过产生[0,1]之间的随机数和搜索空间的上限值、下限值的组合来产生初始个体,并不能保证初始个体在空间中是分布均匀,空间的遍历性较差。本文引入Sin混沌模型来初始化种群,增加麻雀个体在搜索空间中的遍历性,丰富种群的多样性。
(2) 反向学习策略
麻雀种群中的发现者在迭代开始就直接趋向最优解靠近,搜索范围小,易陷入局部最优。为了增强种群的全局寻优能力,引入反向学习策略进行扰动,计算对应的反向解和适应度值,比较该适应度值和种群最佳适应度值,保存适应度更好的解。
式中:Xb(t)和X'b(t)表示当前迭代的最优解和反向解,lb和ub分别表示搜索空间的上限和下限,b1表示信息交换参数,r表示[0,1]范围内的随机数。
2.3 改进麻雀搜索算法ISSA优化ELM的步骤
(1) 采用VMD 对滚动轴承故障信号进行分解并提取样本熵,构建样本熵特征样本,将样本划分为训练样本和测试样本;
(2) 设置SSA的参数,初始化种群规模、最大迭代次数、预警值、发现者比例、侦察者比例、搜索空间的上限和下限,计算麻雀个体的长度即ELM输入层神经元和隐含层神经元之间的连接权值以及隐含层神经元的阈值的长度;
(3) 采用Sin混沌算法初始化麻雀种群,以训练样本期望输出和网络输出的准确率作为适应度函数,计算麻雀个体的适应度值,保存最优适应度值和最差适应度值以及对应的位置;
(4) 根据发现者比例和个体适应度值,选取适应度优的麻雀作为发现者并更新位置,剩下的个体作为加入者并更新位置,同时根据侦察者比例随机选取麻雀个体作为侦察者并更新位置;
(5) 根据反向学习策略对当前代的最优解进行扰动并计算对应的适应度值,比较当前适应度值和种群最佳适应度值,保存适应度更好的解,进行下一次的迭代;
(6) 判断是否达到循环结束条件?若是,跳转至第2步并继续寻优,否则将最优解赋值给ELM 的初始权值和阈值,并结合训练样本进行网络的再学习及训练,最后导入测试样本进行滚动轴承的故障分类。
3 滚动轴承故障诊断仿真试验
3.1 数据分析
为了验证基于VMD 和改进SSA 优化ELM 的诊断模型的有效性和准确性,本文采用美国Case Western Reserve University 实验室的滚动轴承振动数据进行仿真试验[19]。电机驱动端采用深沟球滚动轴承,轴承型号为6205-2RS JEM SKF,轴承的内圈、滚动体和外圈设置电火花单点损伤故障,损伤直径为0.177 8 mm,数据源包括滚动轴承正常状态、内圈故障、滚动体故障和外圈故障的振动信号数据,分别在电机负载功率为0、0.74 6、1.49 2、2.238 kW 的工作状态下采集,采样频率为12 000 Hz。
选取电机负载功率为0.746 kW 的驱动端的振动信号数据,绘制滚动轴承时域波形图,图5-A为正常状态、B为内圈故障、C为滚动体故障、D为外圈故障的时域波形。采样时间为0.3 s,采样点为3 600。本文2.2节通过中心频率和频率混叠性确定了VMD分解的层数为4,分别对滚动轴承的四种状态进行4层VMD分解,见图6~9。
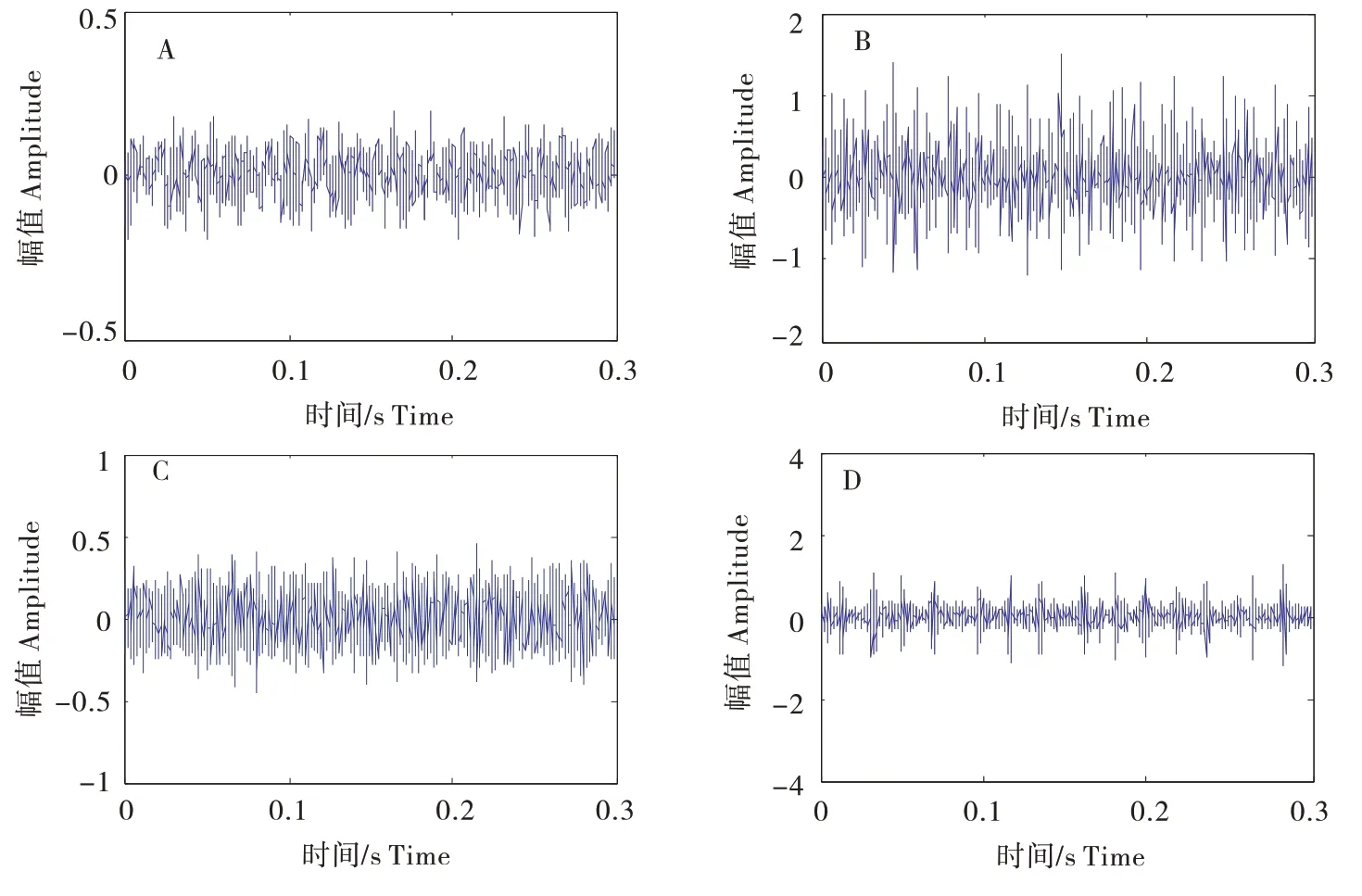
图5 滚动轴承四种状态的时域波形Figure 5 Time domain waveform of four states of rolling bearing
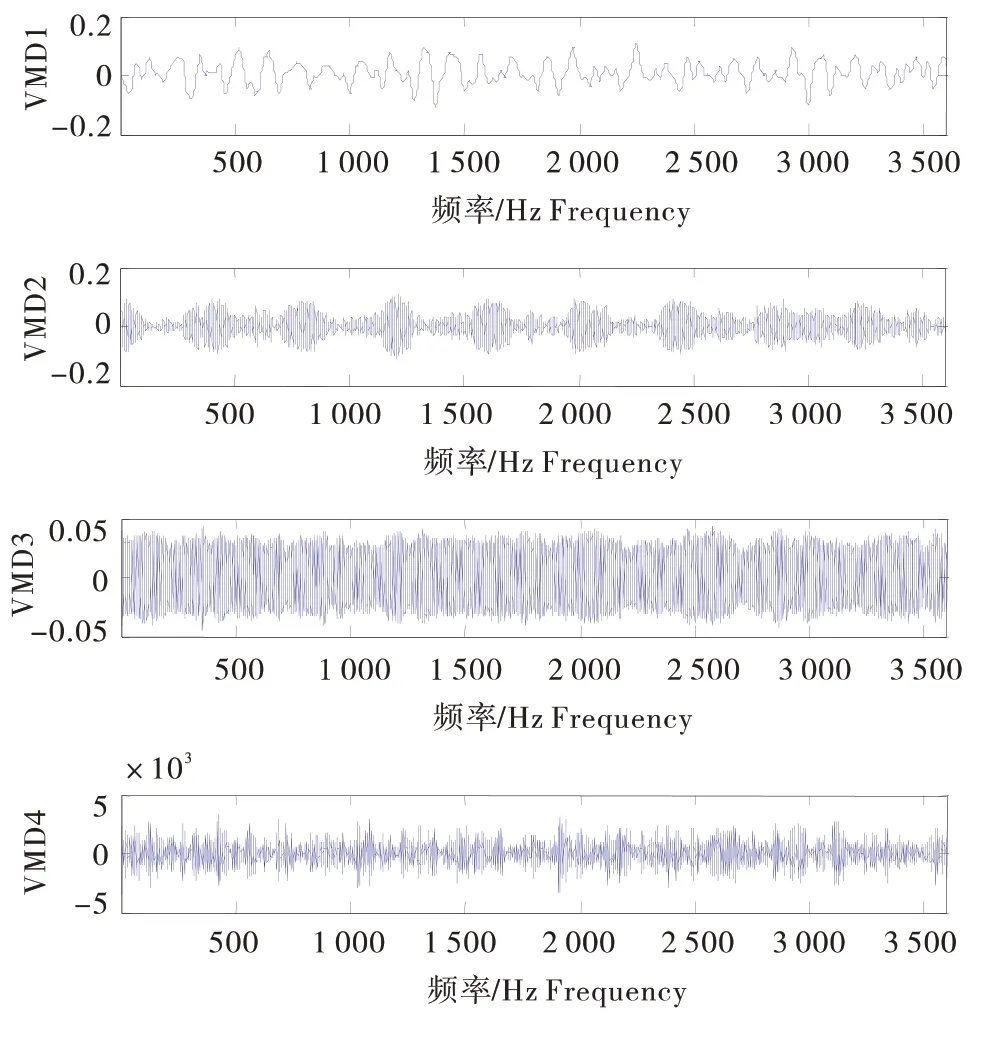
图6 正常状态的VMD分解图Figure 6 VMD decomposition in the normal state
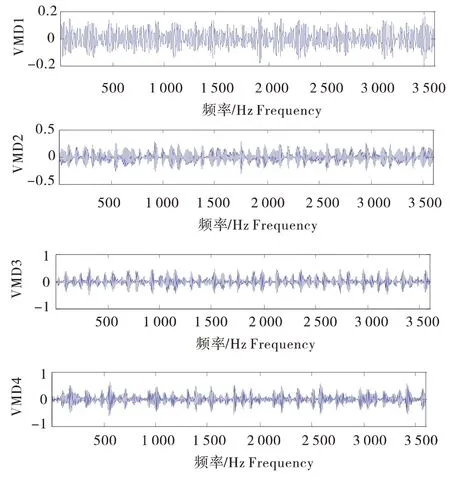
图7 内圈故障的VMD分解图Figure 7 VMD breakdown diagram of inner ring failure

图8 滚动体故障的VMD分解图Figure 8 VMD breakdown diagram of rolling volume failure

图9 外圈故障的VMD分解图Figure 9 VMD decomposition diagram of outer ring failure
3.2 特征样本的提取
在电机负载功率0、0.74 6、1.49 2、2.23 8 kW 的工作状态下,选取滚动轴承内圈故障、滚动体故障和外圈故障以及正常状态的4种类型的振动数据,每种类型在不同的负载功率状态下各采集50组,每组的数据长度为2 000,共计200组,4种类型的数据组数为800组。对数据进行4层VMD 分解,并提取各模态分量的样本熵,样本熵的嵌入维数为2,相似性容限选为各模态序列标准差的0.25 倍,最终得到800行4 列的特征样本矩阵。表2 列出了轴承振动信号经VMD 4层分解后的各模态的样本熵。定义4种类型的分类标签,滚动轴承正常状态为1,内圈故障类型为2、滚动体故障类型为3 和外圈故障类型为4。滚动轴承特征样本信息详见表3。

表2 滚动轴承四种状态的样本熵特征(部分)Table 2 Sample entropy characteristics of four states of rolling bearings (Part)
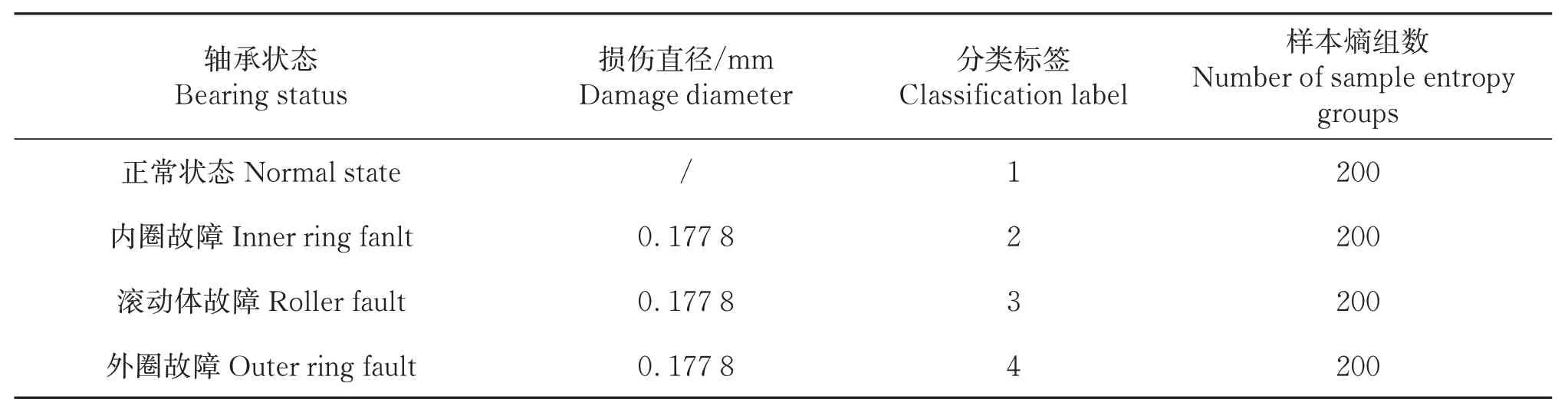
表3 滚动轴承特征样本信息Table 3 Rolling bearing feature sample information
3.3 滚动轴承故障分类识别
采用MATLAB 编程[20]分别建立ELM、SSAELM 和ISSA-ELM 的故障诊断模型,ELM 的输入层、隐含层和输出层神经元的网络结构为4-9-1,传递函数为Sigmoid。SSA-ELM 和ISSA-ELM 中的麻雀种群规模为50,最大迭代次数为300,发现者比例为种群规模的30%,侦察者比例为种群规模的20%,安全预警值为0.7,个体搜索空间的上限为5,下限为-5,根据输入层神经元和隐含层神经元计算麻雀个体长度为45。
特征样本随机划分为训练样本和测试样本,滚动轴承每种类型随机取值170 组共计680 组作为训练样本,剩下的120 组作为测试样本,ELM、SSAELM 和ISSA-ELM 所用的训练样本和测试样本是相同的,SSA-ELM 和ISSA-ELM 的适应度函数为训练样本期望输出和预测输出的分类准确率。将训练样本和测试样本导入SSA-ELM 和ISSA-ELM进行最优解的寻优和故障分类诊断,图10~11 为SSA-ELM 和ISSA-ELM 的迭代过程中种群最佳适应度曲线和平均适应度曲线。对比图10~11,ISSA-ELM 的最佳适应度准确率为98.68%,SSAELM 的最佳准确率为97.79%,ISSA-ELM 平均适应度范围优于SSA-ELM,因而改进的麻雀搜索算法ISSA有更好的全局寻优能力。
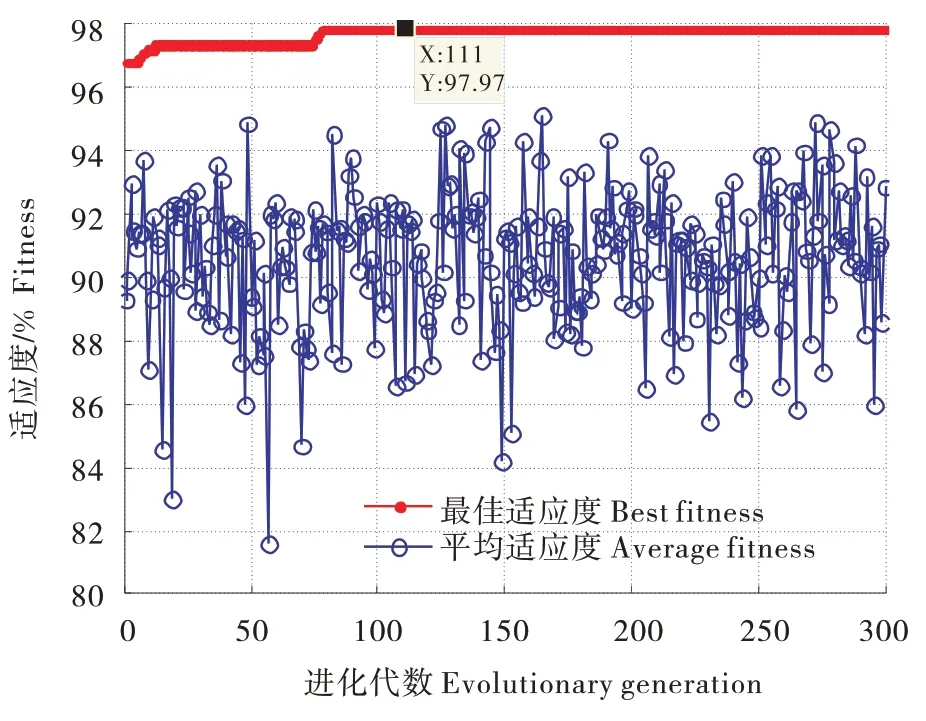
图10 SSA-ELM的适应度曲线Figure 10 Fitness curve of SSA-ELM
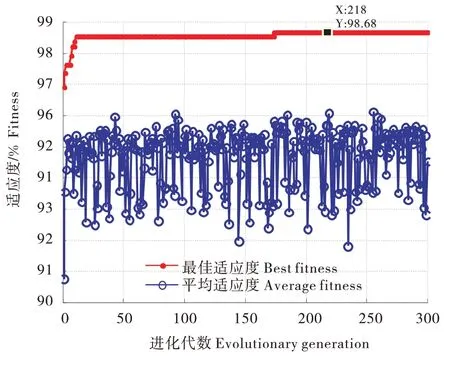
图11 ISSA-ELM的适应度曲线Figure 11 Fitness curve of ISSA-ELM
ELM、SSA-ELM 和ISSA-ELM 对120 组测试样本的分类结果如图12~14所示,3种诊断模型的分类结果对比,见表4。由仿真实验结果可知,ELM、SSA-ELM和ISSA-ELM 3种诊断模型的准确率均超过了90%,对滚动轴承的故障有较好的分类效果。ELM 对测试样本错分了8 个,SSA-ELM 错分了5个,ISSA-ELM错分了3个,错分类型主要集中在内圈故障和滚动体故障两种类型,分析存在的原因为内圈故障和滚动体故障样本熵特征样本中的小部分样本存在相似性,造成模型分类结果的互相混淆。综上所述,ISSA-ELM 相对ELM 和SSA-ELM 的诊断精度更高、泛化性能更优,分类结果验证了本文提出算法的有效性。
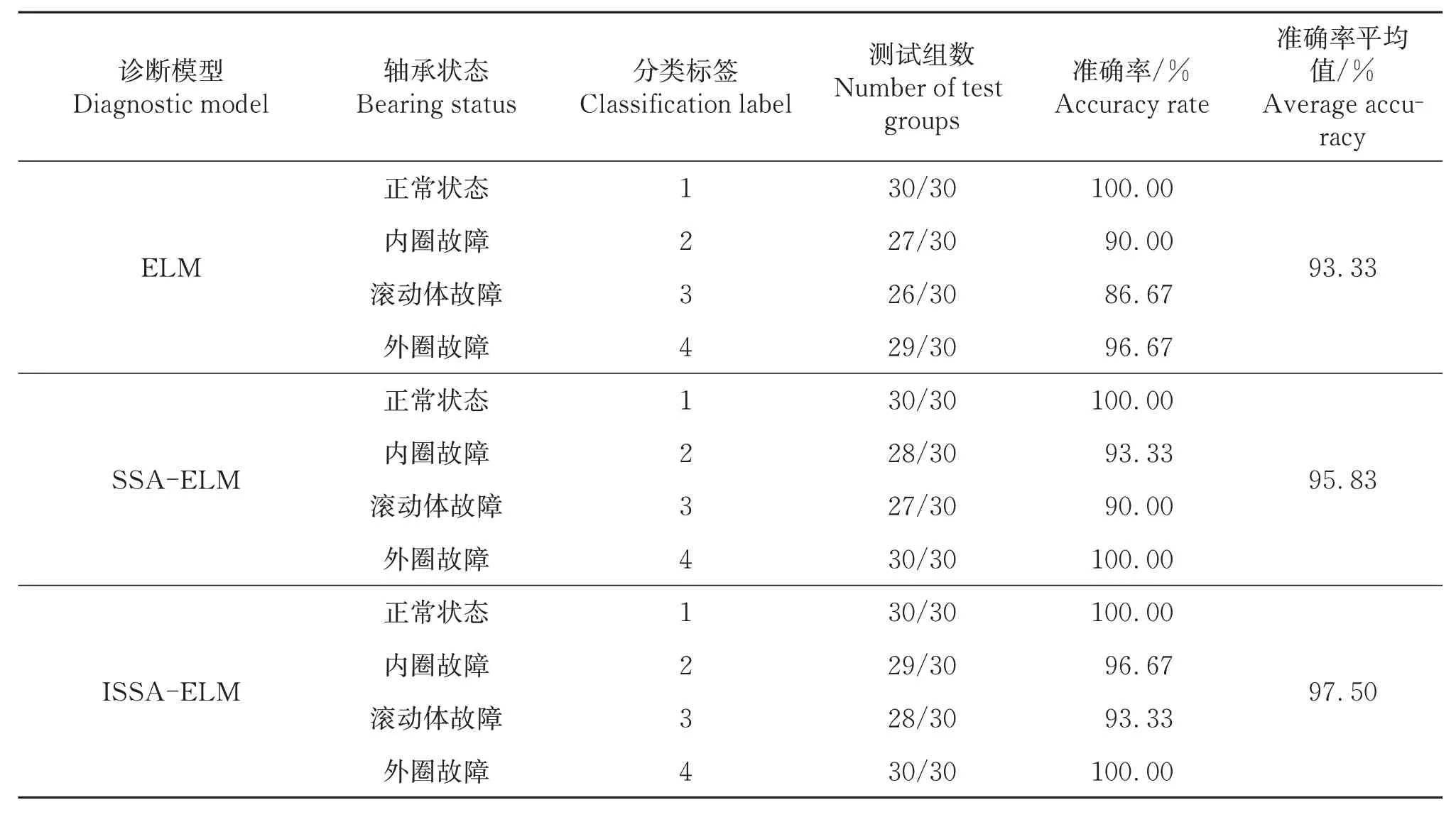
表4 三种分类模型结果对比Table 4 The results of the three classification models were compared
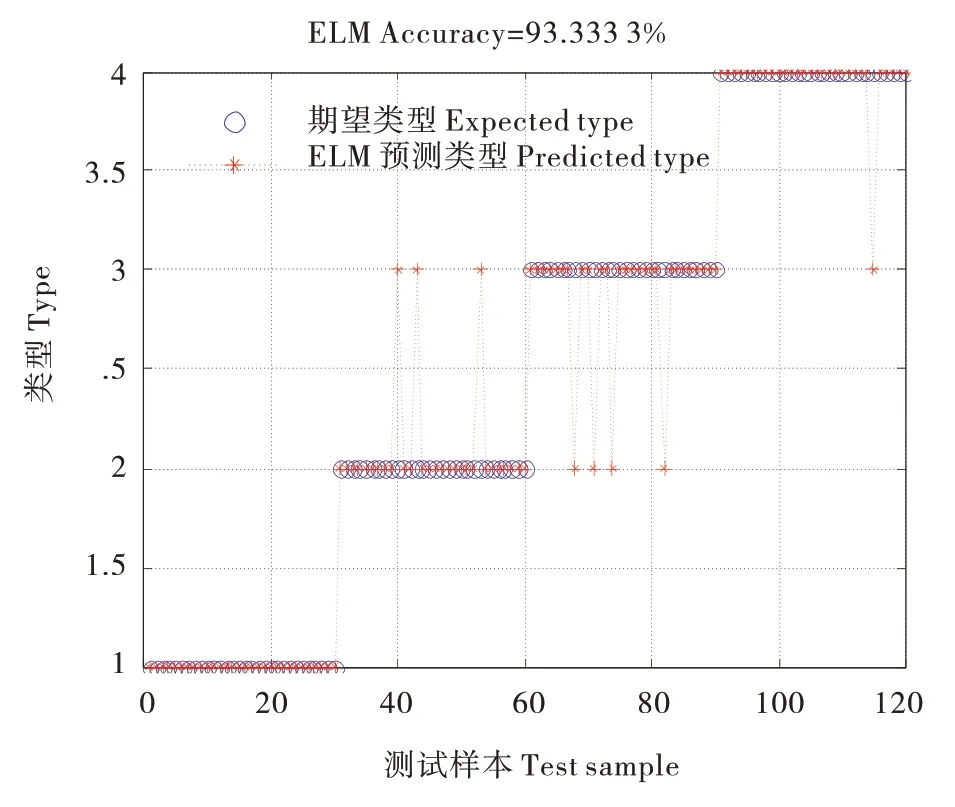
图12 ELM分类结果图Figure 12 ELM classification result diagram

图13 SSA-ELM分类结果图Figure 13 Classification results of SSA-ELM

图14 ISSA-ELM分类结果图Figure 14 Figure of classification results of ISSA-ELM
4 结论
为了更好提高滚动轴承故障诊断准确率,本文提出了基于变分模态分解 (VMD)VMD、样本熵和改进极限学习机(ELM)的滚动轴承故障诊断组合分类方法。以轴承正常状态、内圈故障、滚动体故障和外圈故障的振动信号为研究对象,采用变分模态分解VMD 算法将信号分解成多个模态分量并提取样本熵作为分类特征,构造了改进SSA 优化ELM(ISSA-ELM)的诊断模型,仿真实验结果表明,该模型精度更高、泛化性能更优、诊断识别效果更好,为滚动轴承故障诊断提供了一种新的有效方法。由于在诊断过程中,内圈故障和滚动体故障的类型识别出现了部分相互混淆现象,今后将进一步研究对以上类型的信号进行精细化处理,以更好地提取特征并实现更精确的诊断。

