基于霍尔传感器的汽车天窗防夹系统设计

李 博,宫迎娇,张元良

(1.大连理工大学机械工程学院,辽宁大连 116024;2.传感器国家工程研究中心,辽宁沈阳 110043;3.沈阳仪表科学研究院有限公司,辽宁沈阳 110043)

0 引言

根据市场调查,目前带有天窗的轿车的市场占有率约为70%,用户再次购车时对天窗的配置意愿高于95%[1]。在我国《乘用车内部凸出物》中规定:在电动车窗和天窗开口的4～200 mm处,防夹力应不大于100 N[2]。

当前用于汽车车窗防夹的控制算法以基于电机纹波电流防夹控制和霍尔传感器的防夹控制为主。王晓明等[3]使用霍尔传感器和电机加速度的防夹策略,通过霍尔脉冲信息,反映在运行过程中遇到的防夹力。杜延海[4]等设计了双霍尔的防夹方法,分别感应电机的位置和力矩,提高了车窗防夹的准确性。李丹丹[5]采用了根据霍尔脉宽计算速度,进而计算速度差的方法实现了防夹功能。文献[6]提出捕捉纹波电流的跳变和平均值,将平均值和阈值进行比较,来判定是否触发防夹的方案。李云等[7]在直流分量上叠加的纹波分量来获得位置信息,再对电流值进行积分,判断电机受力情况。苏洪等[8]提出了摩擦力的分离算法,设计了自动更新参数,提高了系统的适用性。史敏杰等[9]在天窗控制器领域首次加入了模糊控制,并通过了最终测试,实现天窗防夹功能。

由于电机的纹波电流易受到外界电磁干扰,提取纹波电流信息困难,且纹波个数易丢失,导致位置零点漂移[10]。而霍尔传感器可以直接反映电机转动的速度、位置以及受力情况,拥有较强的抗干扰性。对于汽车天窗而言,在起翘-滑动过程中,由于机械阻力,电机的载荷发生剧烈变化。因此在天窗起翘-滑动过程中极易出现误防夹的情况。

针对此问题,本论文结合具体的天窗产品,提出基于高斯模型的汽车天窗防夹控制算法。建立的防夹区域的高斯分布模型,由最大似然函数确定防夹区域的模型参数。通过模型判断样本点是否异常。将异常点与模型均值做差分计算,以消除机构阻力带来的影响,差分结果与比例因子的乘积进行窗口内累加计算,通过累加和与标定的阈值比较,判断是否发生防夹。经实验证明,该方法可以有效降低误防夹的发生。

1 天窗防夹系统模块组成

天窗防夹系统主要由控制单元模块、霍尔采集模块、电机驱动模块等组成,如图1所示。

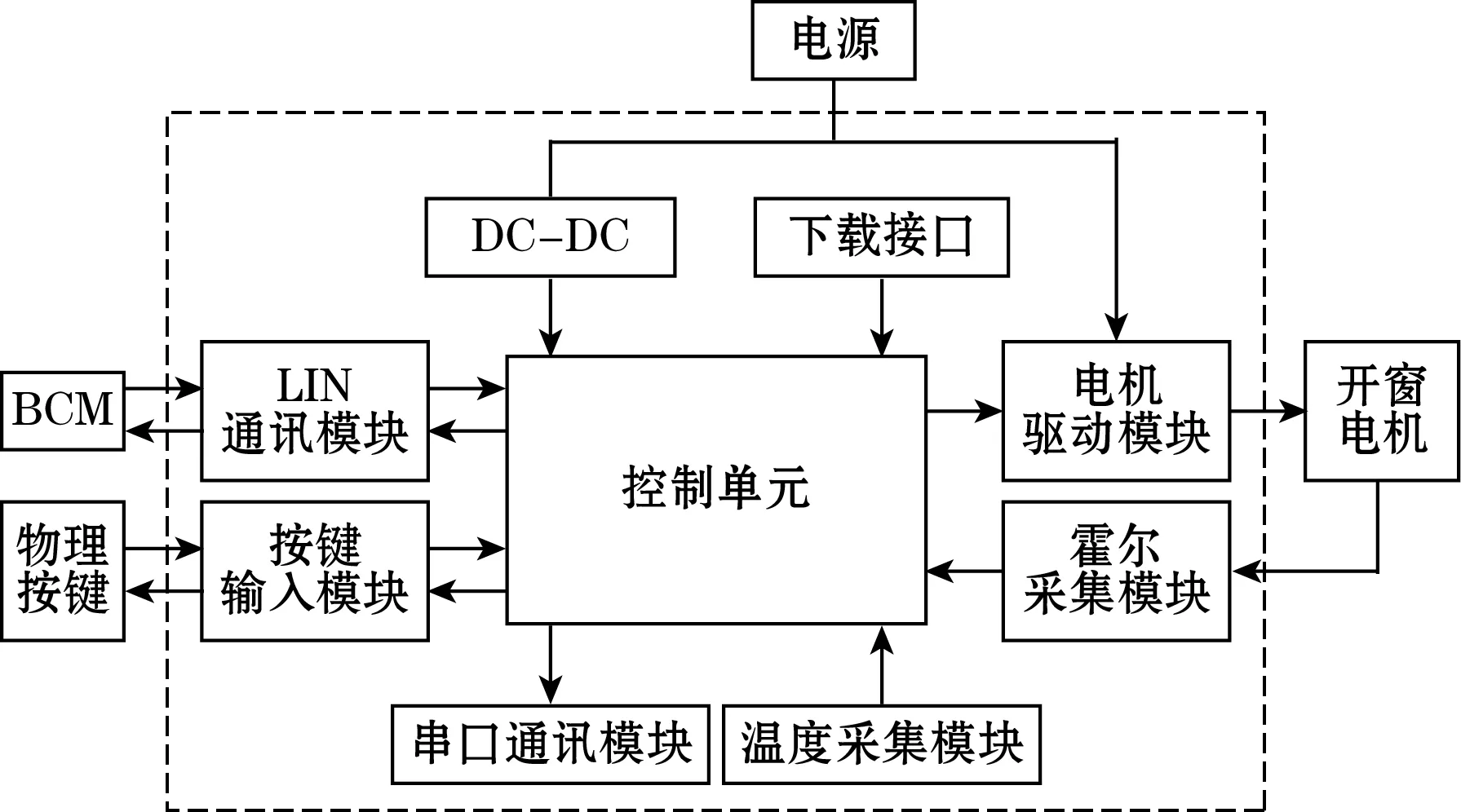
图1 天窗防夹系统模块组成框图

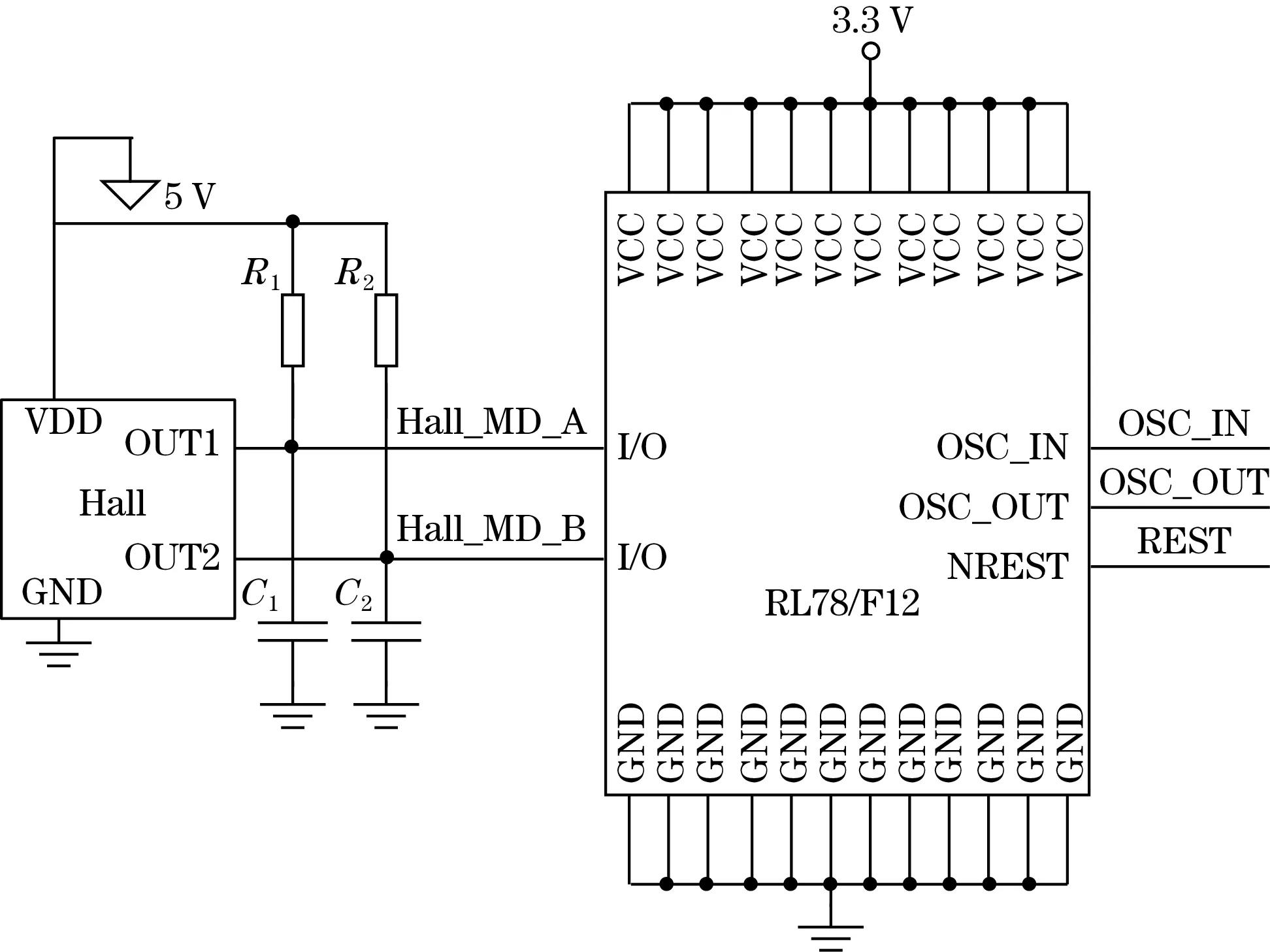
图2 MCU与霍尔传感器原理图

1.1 控制单元模块

控制单元模块负责开关输入、电机启停、转向等核心控制功能。MCU使用瑞萨的RL78/F12系列。霍尔传感器通过感知电机磁环的磁极变化产生霍尔脉冲,霍尔信号通过I/O端口被单片机采集。

1.2 电机驱动模块

天窗电机使用直流电机驱动,通过MOS控制双路继电器的通断,继电器通过吸引不同衔铁控制电机通路的电流方向,天窗电机驱动模块原理图如图3所示。

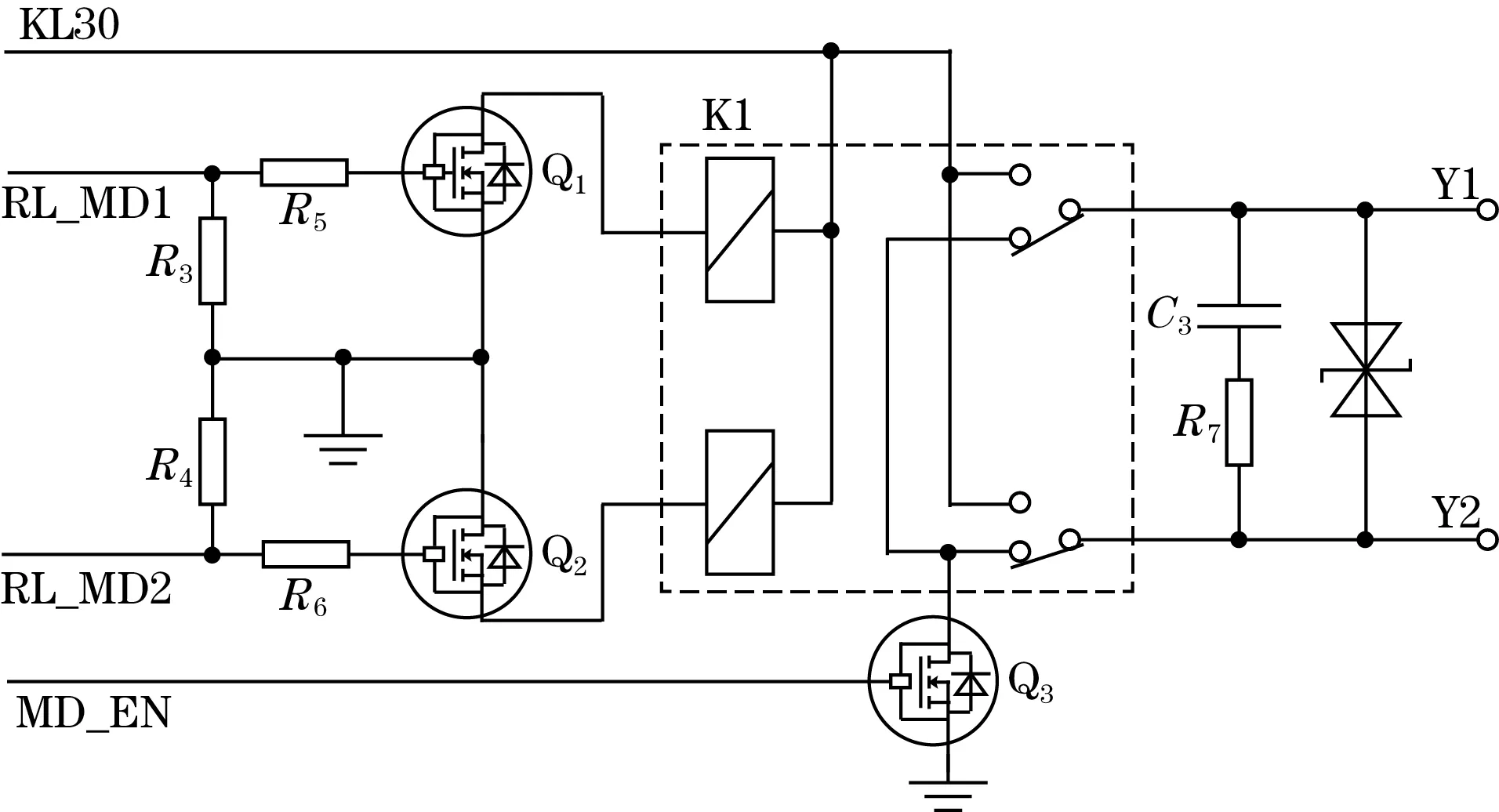
图3 天窗电机驱动模块原理图

2 天窗防夹系统软件设计

2.1 天窗防夹系统软件方案

方案软件分驱动层、中间层、应用层,如图4中所示。该软件分层架构的主要优点是将驱动层与应用层进行单独封装,提高系统软件模块的可移植性。

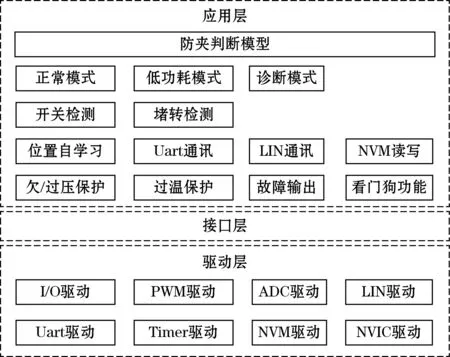
图4 系统软件分层架构

2.2 天窗防夹判断模块设计

防夹流程控制如图5所示。在从LIN总线或开关模块获取到天窗闭合信号之后,MCU模块控制天窗电机转动,将采集的霍尔信号,经过防夹判断模型,判断是否触发防夹,触发防夹后,电机反转;判断是否到达关闭位置,到达位置后,电机停止转动。

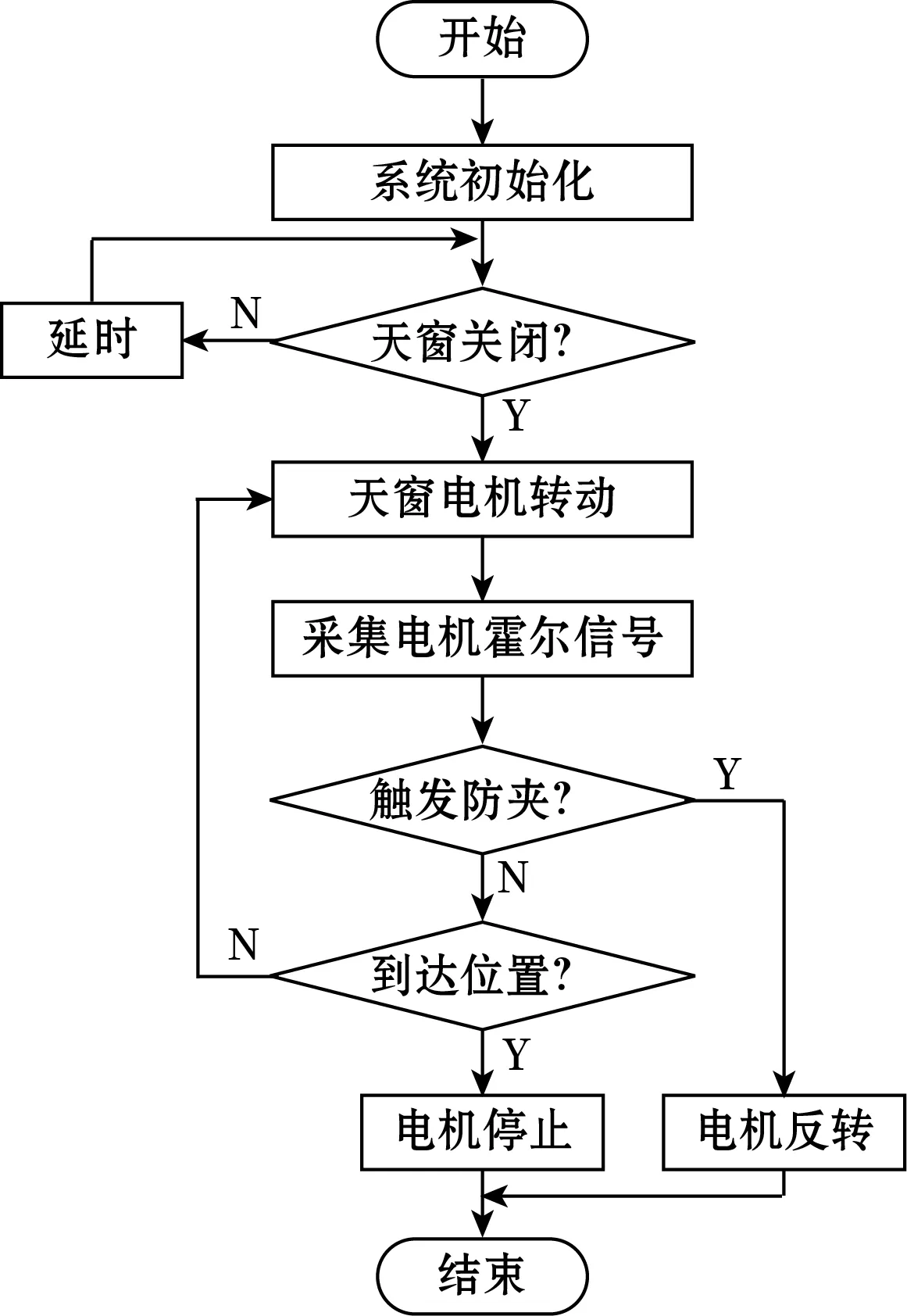
图5 防夹控制流程图

3 基于高斯分布的天窗防夹模型的构建

基于高斯分布的异常检测算法[11]的核心思路是:通过样本集学习并拟合高斯分布模型,当新样本点到来,会将低概率的新样本点当作异常点,视为发生异常。低概率样本点如图6中阴影部分所示。

图6 高斯分布曲线

在12 V系统电压下,采集100组在未遇到加持物的情况下的霍尔脉冲宽度样本,图7为样本集合中霍尔脉冲数为400处的霍尔脉宽分布直方图。

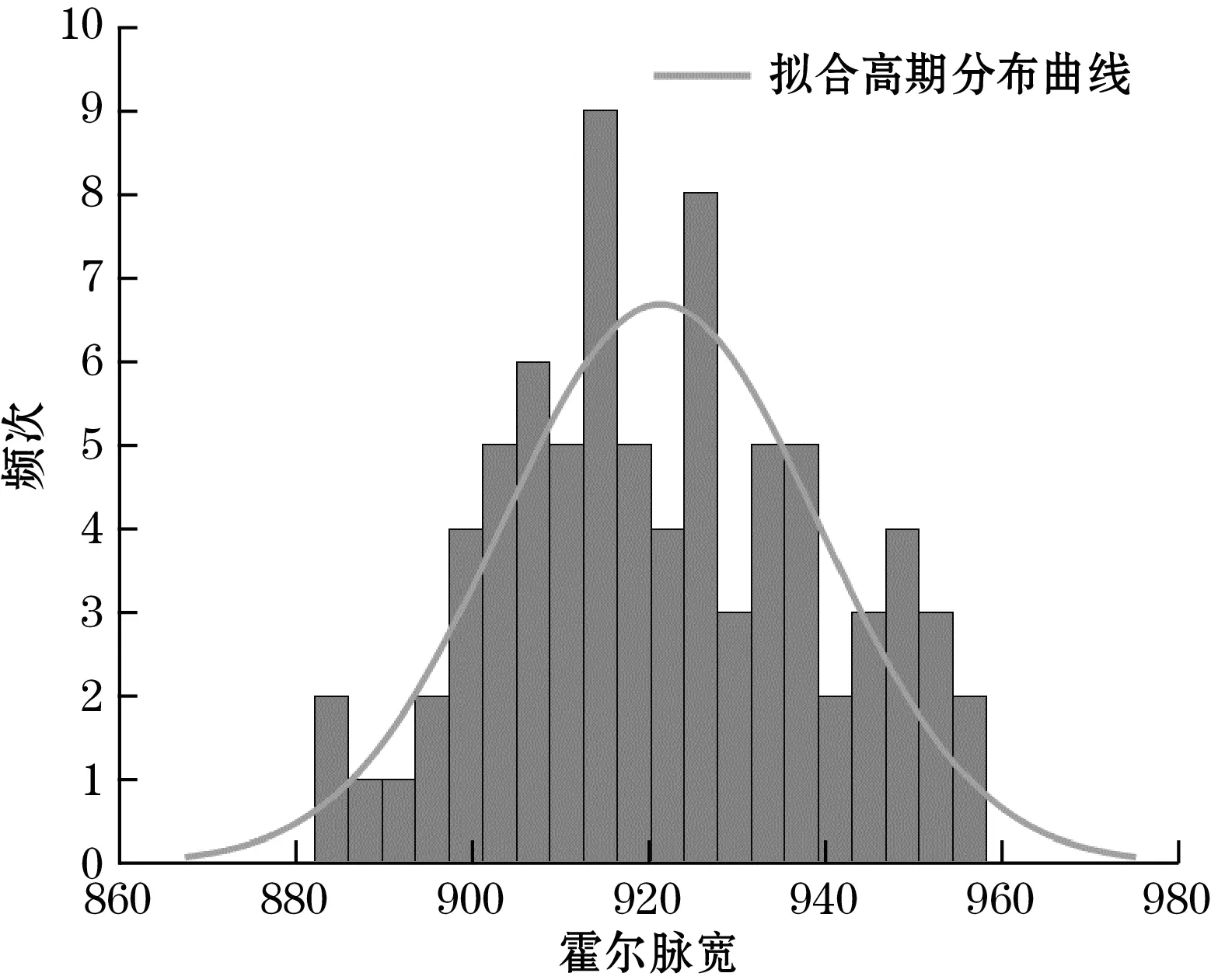
图7 霍尔脉冲宽度直方图

由图7可得,在12 V电压下,该位置的霍尔宽度分布接近高斯分布。假设在天窗的运行过程中,某一位置的霍尔脉宽在多次运行过程中的分布规律,符合高斯分布。经计算在该位置样本均值μ=921.13,样本方差S2=17.932 7。

3.1 模型样本数据获取

在天窗完整关闭过程中,采集防夹区域的霍尔脉冲宽度。如未遇到加持物阻力的情况下,称为一组正常的数据,记为Ni。则第i组正常数据,位置1～m的样本数据集可表示为

Ni=[x1x2x3…xm]

(1)

将n组的正常关闭过程中的样本集合记作Tn,可以表示为

(2)

3.2 基于S高斯的防夹判断模型

防夹判断模型分为两部分,一部分是高斯模型参数提取模块,一部分是防夹判断模块。

高斯模型特征提取模块是确定某一位置的霍尔脉宽高斯分布模型的均值和方差。防夹判断模块是根据霍尔脉宽在高斯分布中的偏离程度,计算是否触发防夹。其中高斯模型的数学表达式为

(3)

由样本集合得到1～m位置处模型的均值和方差,不同位置的均值和方差组成均值矩阵和方差矩阵表示为:

Uμ=[μ1μ2μ3…μm]

(4)

(5)

由此,特征提取模块建立1～m处的高斯分布模型。

记一个新样本为x,新样本的高斯分布的数值记为p(x;μ,σ2),设置概率阈值记作ε,如满足式(6),则该样本点是异常点。

p(x;μ,σ2)<ε

(6)

如果该样本点异常,将当前样本点的霍尔脉冲宽度与样本均值做差分计算,如式(7)所示,差分结果记作pwdiffi,当前霍尔脉冲宽度记作pwi,当前的样本均值记作μi,其主要目的是消除机构阻力带来的影响。

(7)

式中pwdiffi反应当前霍尔脉冲宽度偏离样本均值的偏离程度,对其作窗口内累加计算,累加和使用si表示:

(8)

式中:αi为样本点与样本异常边界ε的偏离程度。

αi表达式为

(9)

提出此比例因子使得pwdiffi×αi在[0,+∞]上连续,并且在未遇加持物的运行过程中,对于可能邻近ε的异常点,其比例因子较小,累加和si较小,减小了天窗误防夹的可能;在遇到加持物时,对于远小于ε的异常点,其比例因子较大,累加和较大,又保证了防夹的准确性。所以,此比例因子的提出是合理的。

累加和si作为当前的夹紧力评估值,防夹阈值记作sT,如果满足下列关系,即判定触发系统防夹。

si>sT

(10)

由此,建立了防夹判断模型。

3.3 基于高斯的防夹判断模型参数确定

已知样本集Tn,最大似然函数表示为

(11)

其对数似然函数为:

(12)

最终,求得正态分布的最大似然估计量为:

(13)

(14)

由此,得到1～m的样本集合的均值和方差,利用样本参数代替总体参数[12],得到集合的均值矩阵Uμ和方差矩阵Uσ2。

4 试验验证

4.1 实验数据获取

采集用于获得防夹判断模型的样本集合Tn,在防夹区域30～200 mm内,共采集天窗闭合样本数据100次。图9为MATLAB输出的样本集合的三维数据图,其中x轴为天窗的霍尔脉冲个数;y轴为样本集合的实验组数;z轴为霍尔脉冲宽度。

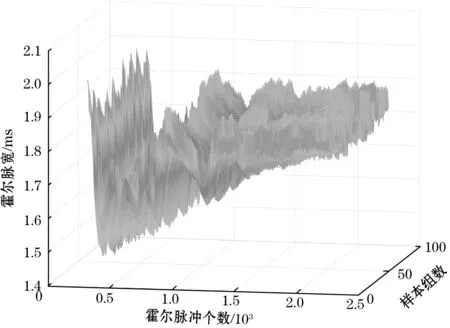
图9 测试样本三维视图

测试仪器采用德国Drive Test FM200仪器作为防夹测试的测试仪。该测试仪主要用于天窗、车窗升降器等的夹紧力测量。将天窗的防夹区域每10 mm进行一次防夹测试且夹紧力设置为(80±3) N采集18组的霍尔脉宽数据作为待测数据,绘制二维图,如图10所示。

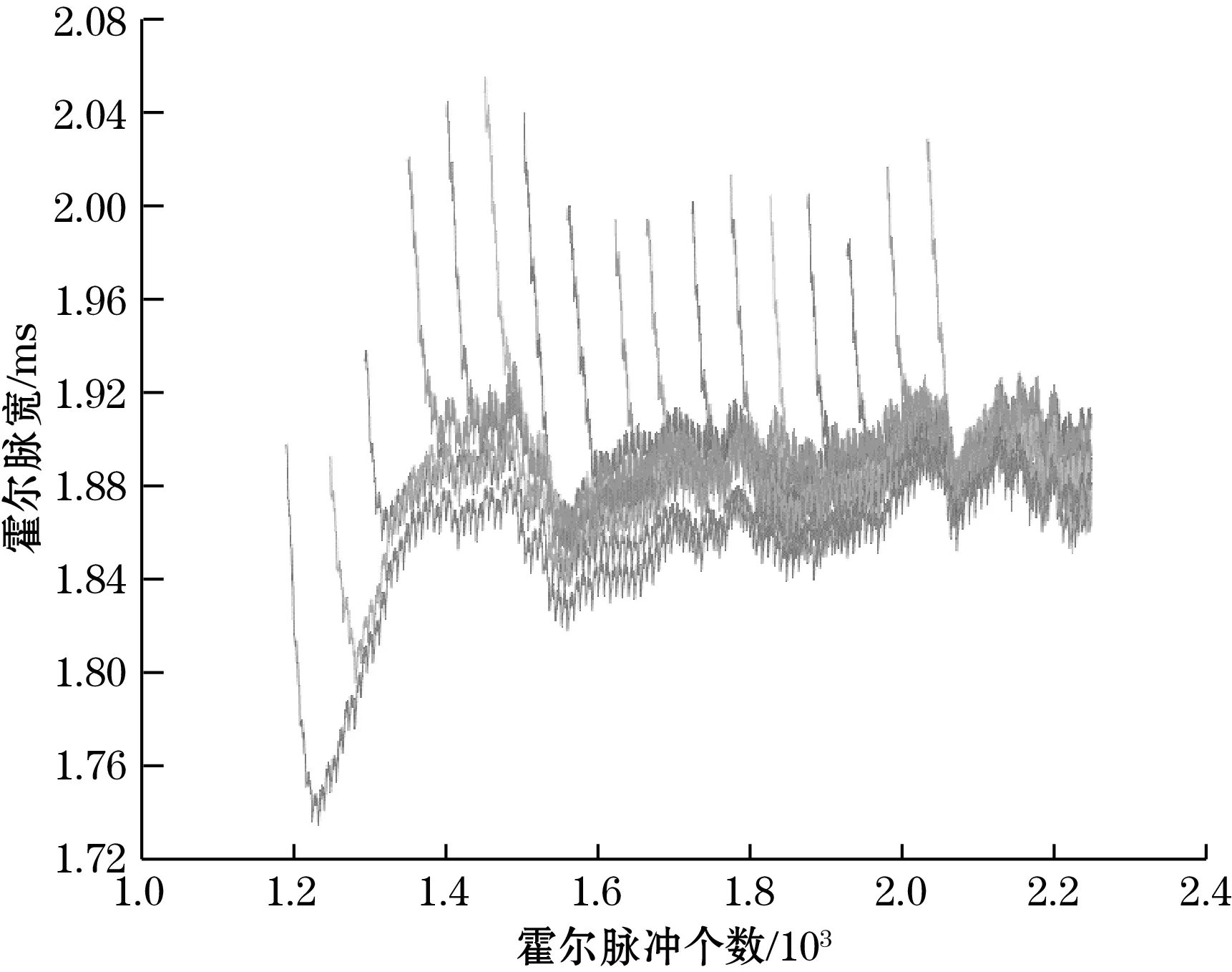
图10 待测数据霍尔脉宽与数量对应关系

4.2 MATLAB模型验证

根据上文方法和数据,使用MATLAB搭建高斯模型,并确定高斯模型的模型参数,经计算,不同位置处的均值和方差如图11所示:

(a)样本集合均值曲线

在天窗的关闭过程中,霍尔脉宽均值与受到的机构阻力相关,变化剧烈。但方差波动较小,样本数据分散程度较为平稳。由此得到样本集合的均值矩阵和方差矩阵。

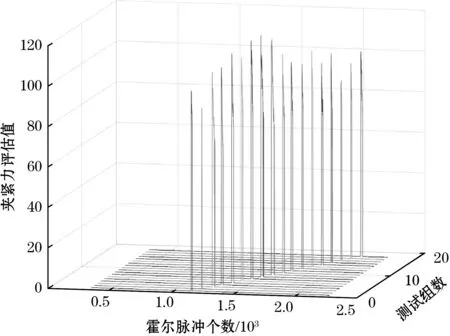
将均值矩阵Uμ和方差矩阵Uσ2以及测试样本集合Ttest作为输入,概率阈值ε=0.000 02,经计算其夹紧力评估值si的三维视图如图12所示。

(a)正侧视图

由图12可以看出,在夹紧力为(80±3) N时,其夹紧力评估值s=100左右,保守计算可以将防夹的判定阈值sT=80。

传统的车窗的防夹算法,使用窗口内的霍尔脉宽进行差分,再进行近似积分,得到夹紧力评估值与阈值比较,判定是否触发防夹。使用正常关闭的天窗霍尔脉冲数据,将基于高斯模型的防夹方法与传统防夹方法进行比较,如图13所示。

(a)传统防夹算法

可以看出,传统算法在天窗关闭过程中,发生剧烈变化,在125、111、113处的夹紧力评估值较大,通过单一的阈值判断是否触发防夹在天窗领域已经不再适用。而基于的高斯模型的天窗防夹算法,由于消除了机构阻力的影响,并对样本点进行异常检测,对异常点进行窗口内累加运算,所以得到一条在0线上方波动的曲线。可以看出,基于高斯模型的防夹算法在汽车天窗防夹领域拥有更好的适用性。

4.3 天窗防夹测试

对该算法进行防夹测试,在天窗防夹区域内,每10 mm进行5次天窗的防夹测试,通过串口上位机显示天窗运行过程中霍尔信息,并记录每次到达防夹位置处天窗触发防夹,并回退过程中最大实际防夹力。其防夹数据的记录如表1所示。

表1 天窗防夹测试结果

由表1可看出,天窗在不同位置防夹力均在85 N以下,能够满足设计要求。

5 结束语

针对汽车天窗在起翘-滑动过程中存在的机构阻力导致天窗的误防夹问题,提出了基于高斯模型的天窗防夹算法。通过建立不同位置的霍尔脉宽的高斯模型,对本次采集点进行异常检测,判断该样本点是否异常,排除正常样本点对于累加结果的影响。将异常点与样本均值进行差分计算,再进行窗口内累加计算,降低了变化剧烈的机构阻力对于霍尔脉宽的影响,最终夹紧力评估值s变化平稳,未出现剧烈变化,提高了算法的稳定性。经天窗防夹测试,实验结果表明:在防夹力符合国家标准的前提下,可以有效解决天窗起翘-滑动过程中,机构阻力带来的误防夹的问题。