基于MMC 的自修复材料结构与微胶囊的协同优化

李 鹏，张昌有，杜艺博，程文涛，占金青，唐 赣

（1.华东交通大学机电与车辆工程学院,江西 南昌 330013；2.华东交通大学载运工具与装备教育部重点实验室，江西 南昌，330013）

复合材料因其优异的力学性能，被广泛应用于航空航天、汽车和电子等领域。然而，作为一种由多种异质/异形组元材料复合而成的新材料，其力学分散性较大，致使材料在生产和服役中易产生各类损伤，尤其是微裂纹的产生和扩展将引起材料力学性能的劣化，导致构件过早失效。损伤自修复[1]概念的提出为解决这一问题提供了有效途径。

White 等[2]于2001 年首次提出微胶囊型自修复材料，并分析了微胶囊的分散性、几何形状与囊壁对修复性能的影响。Yu 等[3]研究了新鲜、短期老化和长期老化沥青混凝土中微胶囊的形态结构、机械强度、热稳定性以及愈合水平。Khan 等[4]研究表明，加入小直径微胶囊的材料弹性模量有轻微减小，但断裂韧性明显增强，而随着微胶囊直径的增加，材料弹性模量和断裂韧性均开始减小。Choi 等[5]将3D打印的微胶囊嵌入混凝土复合材料中，研究了微胶囊壁厚和打印方向对混凝土复合材料的影响。Wang等[6]采用分子动力学模拟了沿z 轴进行单轴拉伸的微胶囊自愈合混凝土的力学和界面性能。Han 等[7]提出了一种三维演化的微力学模型来定量解释了微胶囊对裂纹损伤的自愈合作用。Nassho 等[8]将微胶囊嵌入到层板中，在短梁剪切试件上进行实验并表明，随着微胶囊浓度和粒径的减小，层合板的刚度和表观层间剪切强度增大但愈合效率也会随着降低。Chowdhury 等[9]通过偶联剂改性方法改善颗粒在复合材料中的分布。在化学方法中偶联剂改性，会增加微胶囊与树脂界面的黏合力，有利于材料力学性能的提高[10-11]。

在国内，王瑞等[12]通过偶联剂对微胶囊表面进行改性，研究了微胶囊在材料中的分布以及改性后自修复材料的拉伸性能。郭瑞泉等[13]通过万能试验机研究了微胶囊直径和用量对环氧树脂力学性能的影响。肖春平等[14]研究了4 种不同粒径（180，230，280，370 μm）的微胶囊及其体积分数对材料力学性能和自修复性能的影响。贺子腾[15]制备并研究了苯乙酸乙酯微胶囊直径和体积分数对自修复涂层性能的影响。李鹏等[16]对自修复载体的无壁化设计和分布开展了一些相关研究，并通过实验研究取得一定程度的成果。

近年来，国内外学者针对微胶囊的体积分数、几何形状及分布等内容进行了大量优化研究，然而优化设计的对象仅限于微胶囊载体，对结构宏观构型与内置微胶囊进行协同优化的研究尚未见报道。研究基于可移动变形组件法，通过自修复材料的结构与微胶囊协同优化，在保证材料与微胶囊力学兼容性的基础上，实现材料的损伤自修复设计。

1 内置微胶囊的二维组件

为实现结构宏观构型和内置微胶囊载体的协同优化，研究基于可移动变形组件法，建立内置微胶囊组件的数学模型。以显式的超椭圆方程描述组件[17]。其表达方式如下

式中：

图1 是对组件中微胶囊中心点坐标的说明。

图1 微胶囊中心点坐标说明Fig.1 The center point coordinates of the microcapsule

在式（1）～式（10）中，χi（x，y）表示内置微胶囊的二维组件；χ0（x，y）表示无胶囊的原始组件，χj（x，y）表示微胶囊；max 表示设计域中有限元节点取值为原始组件与微胶囊在该节点的最大拓扑描述函数值；L 为原始组件在x'方向上的半长；f（x'）表示原始组件在y'方向上的半宽；f（x'）可以根据实际优化的需要改变其参数（h1，h2，h3），表示为均匀宽度、线性变化宽度或二次变化宽度等不同的形式；p 为偶整数，一般取p=6；θ 表示原始组件在二维平面内逆时针方向的角度，内置微胶囊与所在的组件取相同的角度，其中st=sinθ，ct=cosθ；（x0，y0）表示原始组件中心点的坐标；r 表示微胶囊的半径，由组件缩放而来；a 和G 表示为微胶囊的初始参数，其中G 表示两个微胶囊之间的间距，a 表示半径系数，这两个参数决定了微胶囊的大小与分布；（x″，y″）因每个微胶囊的中心点坐标不同，而拥有不同的形式，（x-j，yj）表示第j 个微胶囊的中心坐标；floor 表示向下取整；Idis表示两个相邻微胶囊的中心点长度的距离。图2 为内置微胶囊二维组件图。

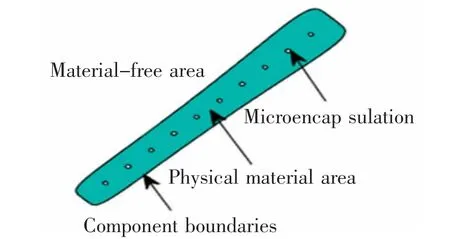
图2 内置微胶囊组件Fig.2 The built-in microcapsules components

2 内置微胶囊拓扑优化问题列式

研究以结构柔度作为衡量材料与微胶囊力学兼容性的指标，考虑给定体积约束下以结构柔度最小为目标函数的拓扑优化，即求出在规定约束和荷载条件下使结构变形最小的最佳拓扑构型。优化列式如下

在式（11）中，C 为结构柔度；Xi=（，sinθi）,i=1，…，n，为第i 个内置微胶囊组件的设计变量；H 为Heasivide 函数；χ 为整体结构的拓扑描述函数；f 为内置微胶囊的二维组件所受的体积力；u 为结构位移场；t 为Neumann 边界Γt上的面力；q 为惩罚因子，这里取q=2；E 为四阶弹性张量，且其表达式为E=E/（1+v）［Ⅱ+v/（1－2v）δ⊗δ］，其中E 和v 分别为实体材料的弹性模量和泊松比，Ⅱ和δ 分别为四阶单位张量和二阶单位张量；ε 为二阶线性应变张量；是实体材料的体积上界；v 为定义在实体材料所占区域上满足Uad=｛v|v∈H1（Ω），v=0 on Γu｝ 的试探函数；UX表示设计变量所属的可行域；为Dirichlet 边界Γu上的给定位移，为了简化分析，文中取=0。

3 数值分析

3.1 二维有限元分析

研究基于MMC 框架的拓扑优化方法，采用“代理材料模型”进行有限元分析，由式（1）计算出每个节点的拓扑描述函数值，则单元格的弹性模量按以下公式插值

式中：为了保证全局刚度矩阵的非奇异性，α 是一个很小的正数；ζ 表示一个正则化参数，其作用是用来控制正则化的宽度。

3.2 灵敏度分析

研究因为基于可移动变形框架的优化方法，因此采用伴随法可直接推导目标函数C 对内置微胶囊组件各个设计变量的灵敏度，如下

以及约束条件V 内置微胶囊组件各个设计变量的灵敏度，如下

在式（14）～式（15）中，x 表示X=（（X1）T，…，（Xi）T，…，（Xn）T）T中的任意变量；K 表示结构的整体刚度，NE 表示单元格的数量；ke表示单元刚度矩阵。

3.3 优化算法

研究采用移动渐进算法（序列凸规划法）作为优化求解器用于对拓扑优化问题的求解。移动渐近线算法最初由瑞典数学家Svanberg[18]最早提出，它是将目标函数和约束条件转化为在当前设计点的一阶移动近似子问题，通过梯度法求解子问题的解作为目标函数的近似解。

4 算法流程

自修复材料结构与微胶囊的协同优化流程如下：

1）设定材料的原始参数、设计域大小、微胶囊参数、载荷等；

2）根据设计域大小，设计合理的网格大小、组件初始化参数、MMA 优化参数；

3）根据微胶囊的相关参数计算组件中每个微胶囊的中心点坐标，在求解整体结构的拓扑描述函数值时，微胶囊与组件相交显示微胶囊；

4）利用有限元求解结构目标函数和约束条件；

5）利用有限差分原理计算目标函数与约束条件的灵敏度；

6）将MMA 作为优化器更新设计变量；

7）判断是否满足迭代终止条件：每100 次迭代的目标函数最优值连续10 次未被更新，则终止迭代。

二维协同优化流程图如图3 所示。

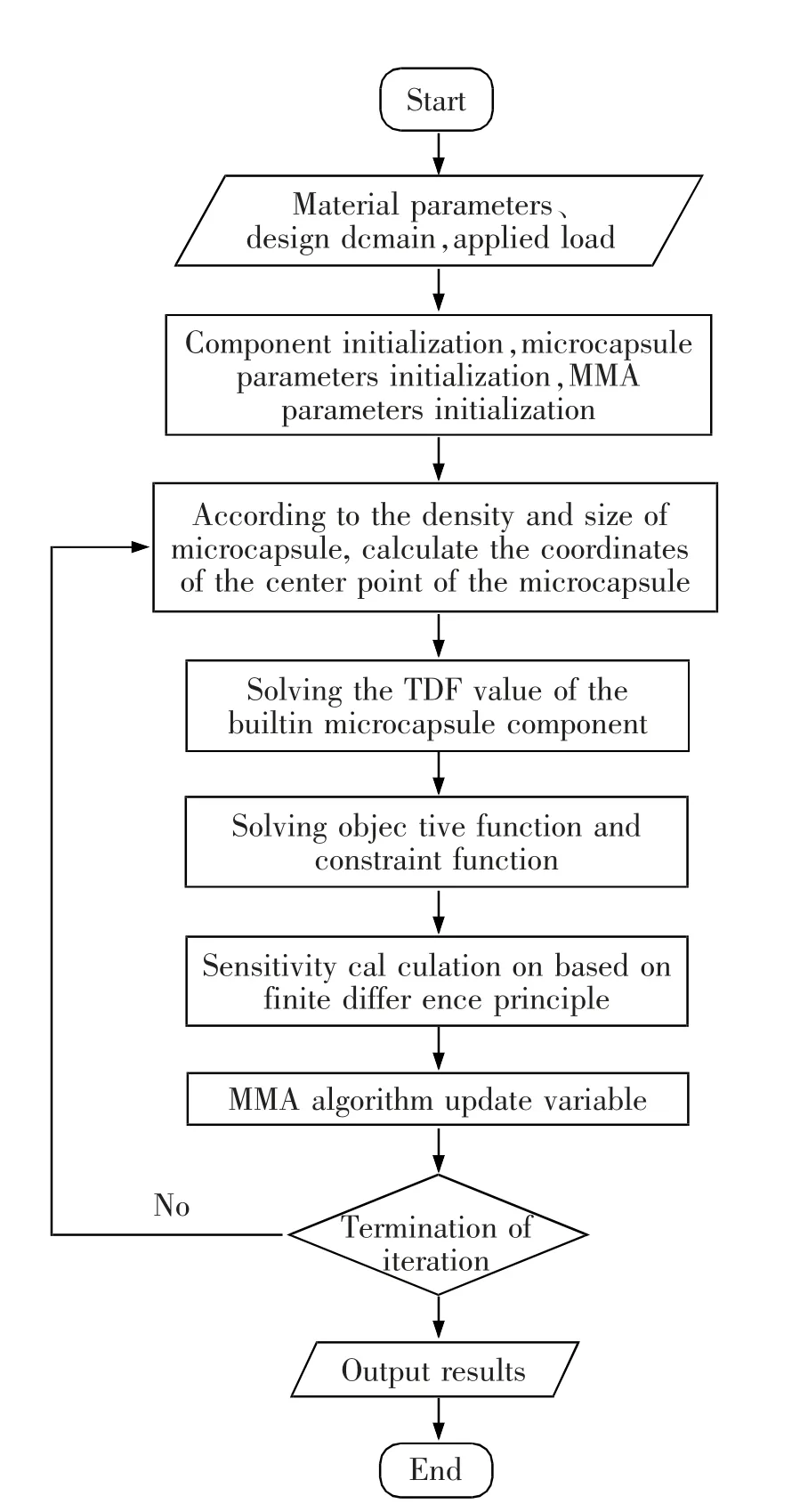
图3 二维协同优化流程图Fig.3 2D collaborative optimization flow chart

5 数值算例

为验证自修复材料结构与微胶囊协同优化的有效性，研究采用二维MBB 梁算例，算例所涉及的弹性模量、材料密度、载荷以及几何参数等信息均为无量纲，实体材料的弹性模量值设置为E=1，泊松比设置为v=0.3。

如图4 所示，以MBB 梁的一侧为设计域，长宽比为3∶1，设计域离散为450×150 的网格，右下角受滚动铰链约束，左下角固定支撑，左上角受到竖直向下的载荷f=1。由于MBB 梁结构在此工况下具有对称性，故优化时只取设计域的一侧，对应的水平网格划分和结构受力都减半，以结构柔度最小为目标，给定的面积约束上限为V≤0.3D，D 为设计域面积。

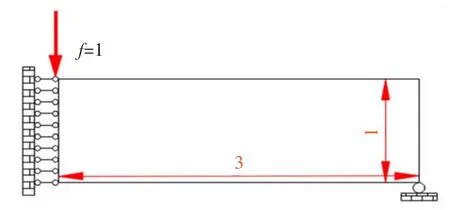
图4 MBB 梁一侧设计域Fig.4 One side of the design domain of MBB beam

图5 为MBB 梁算例的初始设计，算例中共设计24 个组件。表1 给出了组件与微胶囊的初始设计参数。其中，第一和第二个组件的中心点坐标均为（0.25，0.25），倾角的正弦值分别为0.7 和-0.7。其他组件依次沿着x（或y）方向平移0.5 获得，各组件中有6 个微胶囊，微胶囊的半径系数a 为0.1，微胶囊之间的间距G 为0.1。

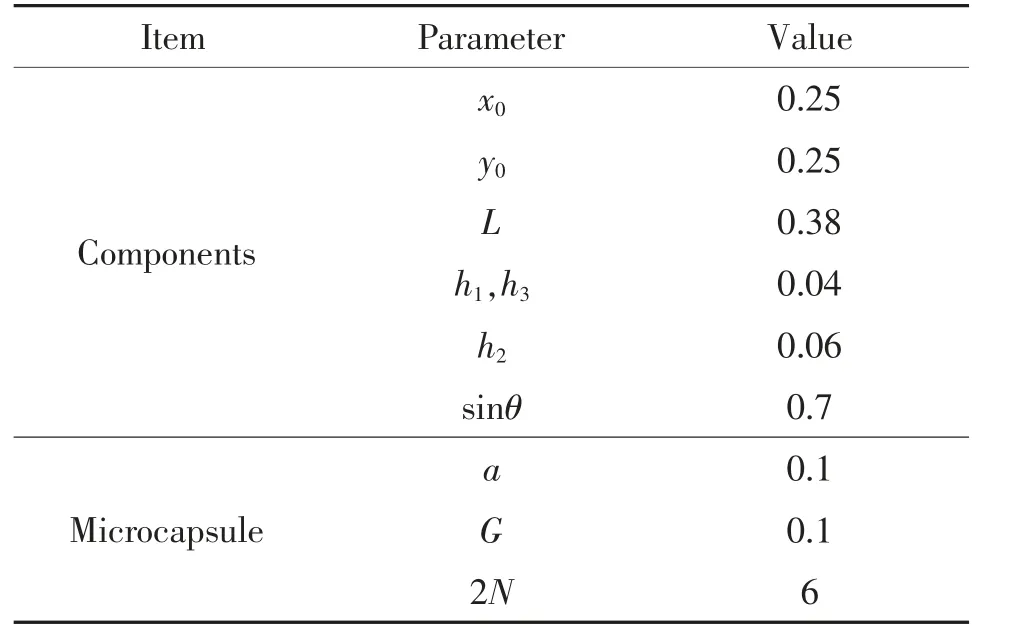
表1 MBB 梁内置微胶囊的组件初始设计Tab.1 Initial design of components with microcapsules in MBB beam

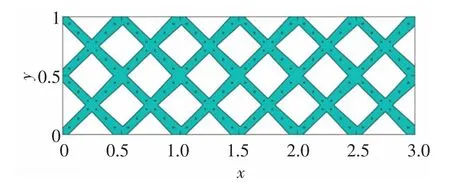
图5 MBB 梁算例初始设计（a=0.1，G＝0.1）Fig.5 The initial design of MBB beam example（a=0.1，G＝0.1）

图6 为基于MMC 方法的自修复材料结构与微胶囊协同优化的结果，即“协同优化自修复材料”。

图6 协同优化自修复材料拓扑优化构型（a=0.1，G=0.1）Fig.6 Optimize topology and configuration of collaborative self-healing materials（a=0.1，G=0.1）

为论证协同优化的效果，研究沿用经典自修复材料的设计方法。首先，基于MMC 方法获取相同初始条件（如工况、边界条件等）下无胶囊载体的拓扑优化构型（如图7 所示，其柔度值为294.6）；其次，根据不同的微胶囊参数，在组件内嵌入微胶囊，设计“经典自修复材料”，并计算相应柔度和微胶囊体积分数（如表2 和图8 所示），微胶囊体积分数是指拓扑优化构型中全部微胶囊所占的面积比，体积分数的取值范围为[0，1）。研究结果表明。

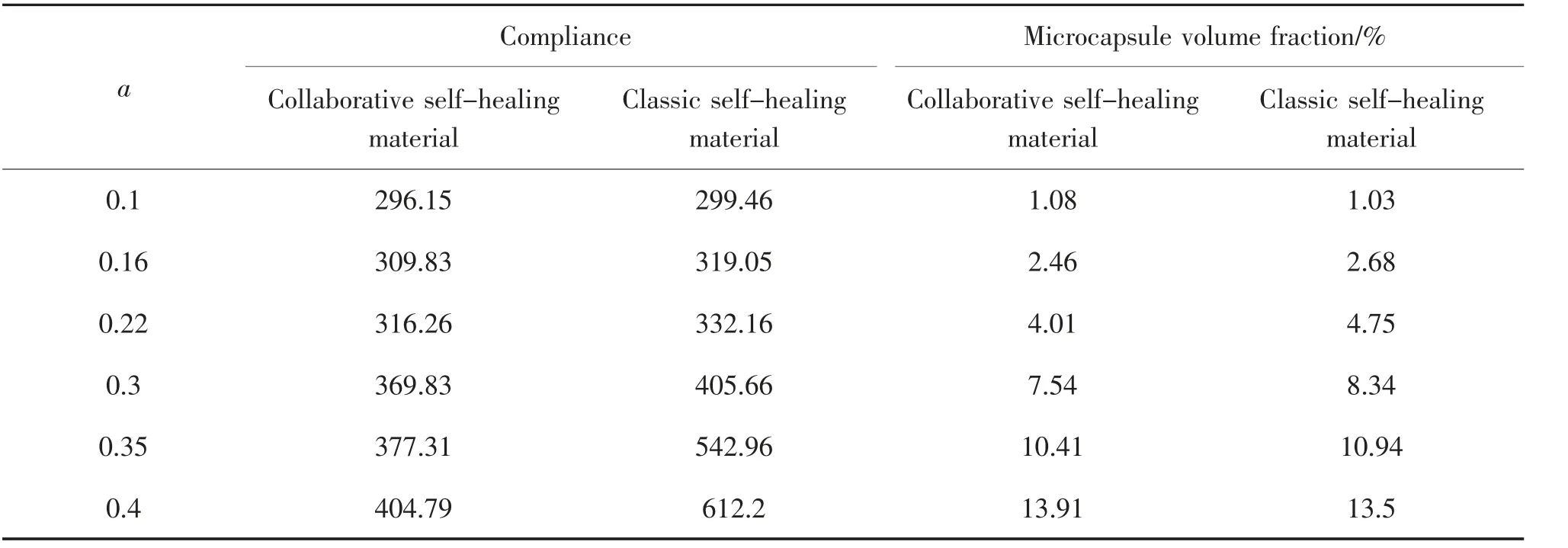
表2 不同微胶囊半径系数a 下两类自修复材料的优化结果Tab.2 Optimization results of two kinds of self-healing materials with different radius coefficients a of microcapsules

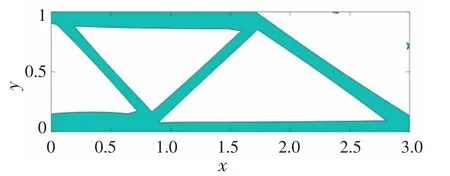
图7 无胶囊载体拓扑优化构型Fig.7 Carrier topology optimization configuration without capsule

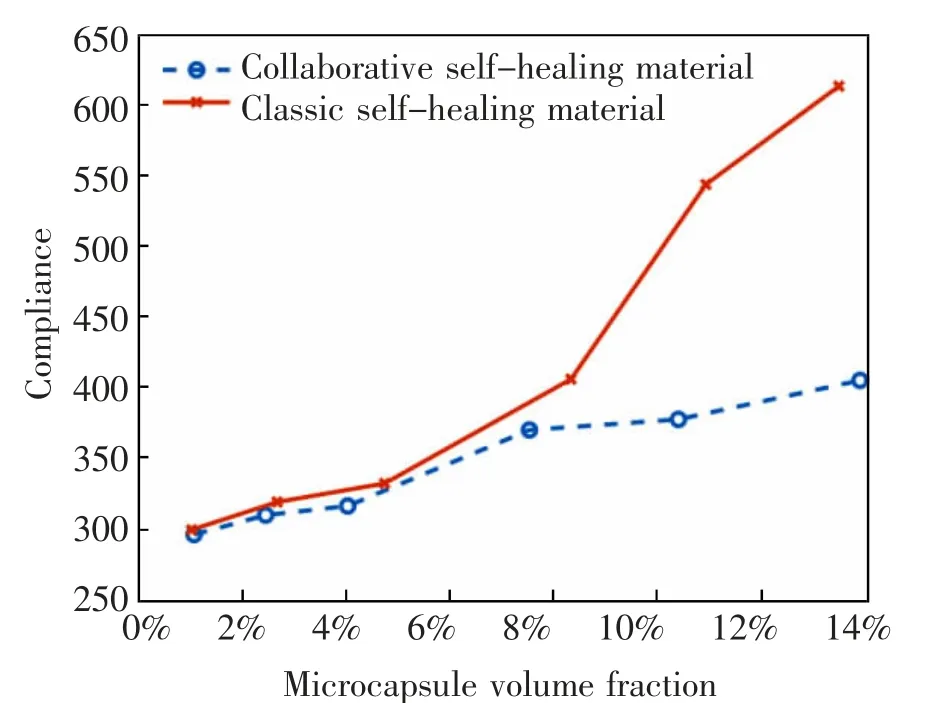
图8 两类自修复材料微胶囊体积分数与柔度关系Fig.8 Relationship between microcapsule volume fraction and compliance of two kinds of self-healing materials

1）对比无胶囊载体的MBB 梁优化构型（图8），协同优化自修复材料（a=0.1，G=0.1）的柔度提高了0.53%，为296.15（表2），且构型具有相似性（图6）。

2）由表2 可知，微胶囊参数决定了自修复材料载体的体积分数，当微胶囊半径系数a 由0.1 增至0.4 时，两类自修复材料的微胶囊体积分数均出现了增加趋势；

3）由表2 可知，随着微胶囊体积分数的提高，两类自修复材料的柔度均出现了增加，然而增加的幅度存在明显差异，图8 为两类自修复材料微胶囊体积分数与柔度关系曲线，显然协同优化自修复材料的柔度均小于经典自修复材料，而且随着体积分数的增加（尤其体积分数大于8%时），两者的差别明显变大。这说明对于经典自修复材料而言，当微胶囊体积分数大于8%时，微胶囊载体将造成结构力学性能的急剧劣化，而协同优化自修复材料则可减小这一不利影响。

4）通过研究不同微胶囊参数下两类自修复材料的构型，进一步分析协同优化的效果。表3 给出了微胶囊半径系数a 分别为0.16 和0.35 的两类自修复材料构型，显然相对于经典自修复材料而言，协同优化自修复材料通过宏观构型的优化有效的减弱了载体对自修复材料力学性能的影响。

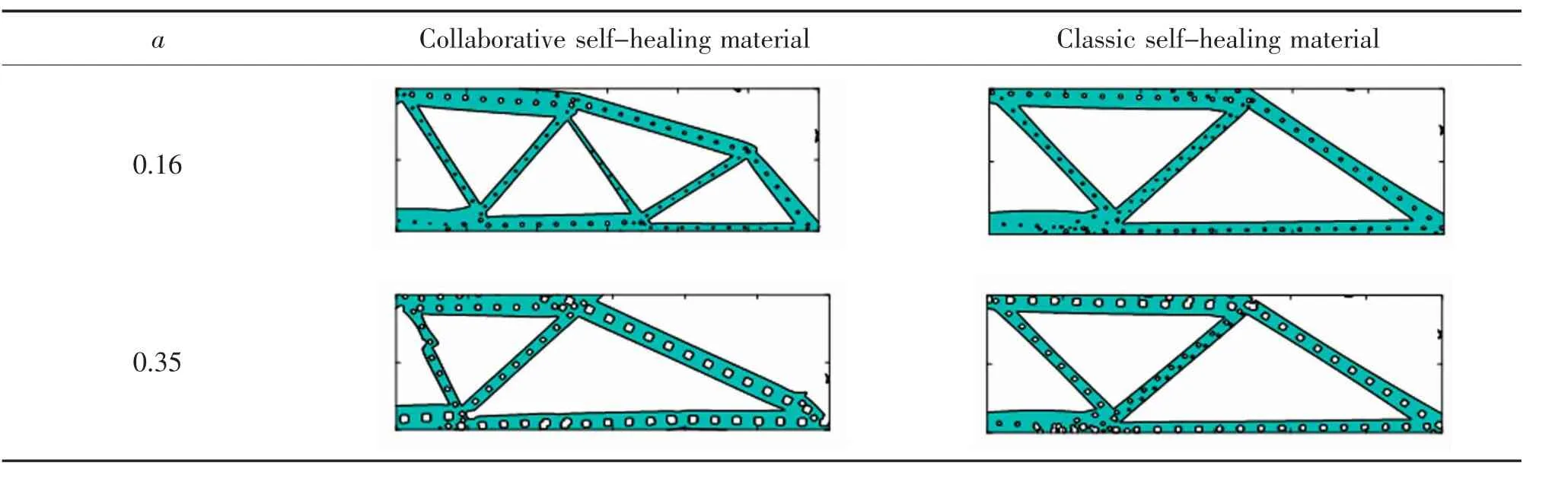
表3 两类自修复材料拓扑优化构型Tab.3 Topological optimization configuration of two self-healing materials

6 结论

1）将无胶囊的MBB 梁拓扑优化构型与内置微胶囊的MBB 梁拓扑优化构型进行了对比，论证了内置微胶囊的MBB 梁在微胶囊体积分数较低的情况时，可以获得与无胶囊的MBB 梁相似的拓扑优化构型，证明了引入协同优化方法的有效性。

2）随着微胶囊体积分数的增加，将会造成两类自修复材料的柔度增大，力学性能的劣化。

3）当微胶囊体积分数超过8%时，对于经典自修复材料，微胶囊会造成其结构力学性能的急剧劣化，当微胶囊体积分数接近14%时，协同优化自修复材料的柔度值仅为经典自修复材料的66.1%。可见研究提出的协同优化自修复材料，通过引入宏观构型与微胶囊的并行优化机制，可有效的减小微胶囊体积分数增加对其结构力学性能的不利影响。