基于特征模型的高速列车自适应误差补偿控制

谭 畅，张耒耒，杨 辉，章俊辉

（1.华东交通大学电气与自动化工程学院，江西 南昌 330013；2.华东交通大学江西省先进控制与优化重点实验室，江西 南昌 330013）

高速列车作为一种快速、高效、节能环保的运输工具，近年来得到广泛的重视和迅猛的发展，已成为现代交通运输系统中不可或缺的部分[1]。然而高速列车轨道情况复杂，工况变化频繁，列车系统因不确定的运行状态和运行阻力等因素都会产生系统误差，进而导致列车运行过程表现出强烈非线性、参数时变、不确定性等运行特点[2-3]。这些系统误差不仅使列车的控制性能变差，还会使得列车运行不稳定，甚至导致安全事故的发生。研究建立有效的高速列车运行过程模型，并设计合适的控制策略实现系统误差补偿，对于保证列车安全运行具有重要的现实意义和实践价值[4-5]。

米根锁等针对高速列车在运行中由牵引和制动系统的损耗现象和外界干扰引起的模型参数偏差问题，设计了一种最优预见控制算法实现的控制器，并进行极点配置保持控制系统稳定[6]。李中奇等为解决动车组停车制动控制中因参数时变和时延导致的较大停车误差问题，提出了一种改进模糊PID-Smith 控制器[7]。何之煜等利用高速列车运行过程因受到外部扰动和系统受限的情况而产生的状态偏差，提出了一种基于迭代学习控制的自适应控制算法，能够用较短的迭代次数实现对期望曲线的精确跟踪[8]。耿睿等将动车组实际输出与线性模型输出的误差描述为未建模动态，设计了多变量非线性广义预测控制器[9]。但上述研究中针对误差引起的问题，大都将其视作可预见的，没有考虑列车运行过程中存在的系统误差大多不可测，因此误差的估计成为误差补偿的关键。针对这一问题，Yang 等总结了各类可用于估计的方法[10]，详细介绍了目前较为常用的干扰观测器和扩张状态观测器（extended state observer, ESO）方法。徐传芳等考虑输入饱和约束以及由于不确定的运行阻力、未知的黏滞摩擦系数和未测量的运行状态等引起的系统不确定性，引入扩张状态观测器在线估计和补偿系统总的不确定性，提出高速列车的鲁棒自适应动态面控制算法[11]。郭亮等将列车运行过程中受到的基本阻力和附加阻力等当作“总干扰”，利用扩张状态观测器对该干扰进行估计，并设计列车速度曲线跟踪的前馈控制算法[12]。上述方法都在一定程度上估计和补偿了系统的不确定性，但高速列车这类属于不确定性复杂对象的控制系统，容易受到人为的干扰中断和启停，致使系统常处于过渡阶段。迫切需要提出一种能够有效解决高速列车由于系统误差导致不确定性和自适应调节问题的补偿控制方法。

自适应控制在实现过渡过程的自适应调节和解决高速列车不确定参数以及渐进跟踪的问题上有着独特的优势，被广泛用于高速列车跟踪控制[13-15]。但大部分自适应控制容易出现待调参数过多，参数预选工作量大以及计算量大的问题，不利于工程实现。而特征模型以其简单的结构和具有输出采样反馈形式弥补了此方面的不足。吴宏鑫等提出的基于特征模型的智能自适应控制理论[16-17]可以解决一类复杂的高阶对象或者非线性系统对位置保持或者跟踪的控制要求。曹阳等针对高速永磁同步电机调速系统因物理受限产生的饱和效应，设计了一种基于特征模型的自适应抗饱和控制，提高了系统跟踪精度和抗干扰能力[18]。吴悠等为实现对管道压力的高精度控制，将特征建模与黄金分割自适应控制应用于水流管道的压力控制[19]。Gao 等为实现对列车位移和速度的精确跟踪控制，提出了基于特征模型的全系数自适应控制，设计了位移/速度双反馈的控制方法，将其应用于列车自动控制系统中，具有较强的鲁棒性[20-21]。可以看出，应用特征模型方法处理具有较大不确定性的系统和被控对象，在控制性能上具有出色的表现。

本文针对高速列车运行过程中因系统误差造成的不确定性问题，提出了一种新的基于特征模型的高速列车自适应误差补偿控制策略。该策略通过建立存在系统误差的高速列车特征模型，考虑不确定运行阻力、辨识误差及模型误差等对系统的影响，设计扩张状态观测器对其进行估计以达到补偿目的，实现列车对给定目标曲线的渐近跟踪。

1 列车动力学建模和问题描述

1.1 列车系统动力学模型

在列车动力学中，考虑到高速铁路线路坡度长、曲线半径大，可以将在其上方运行的高速列车看成一个质点。列车整体动力学模型可以描述为

式中：v 为列车运行速度；γ 为加速度系数；F 为列车受到的合力；u 为列车牵引力或制动力；Fg为列车基本阻力，a，b，c 为阻力系数，三者均为非恒定系数，且变化范围较大。将式（1）整合，可以得到如下的动力学方程

随着列车运行速度的不断提高，cv2所占比例越大，系统的非线性特征就越明显，式（2）即为高速列车的非线性模型。

1.2 列车特征模型

鉴于特征建模方法可以结合被控对象动力学特征、环境特征和控制性能要求进行建模，本文通过特征模型方法建立列车特征模型。特征模型一般用一阶或二阶时变差分方程来描述，有关信息都压缩到几个特征参数中，不丢失原有的信息。并且建立形式比原对象动力学方程简单，易于实现，能够有效解决高速列车控制设计中系统模型阶次较高和模型建立过程较为复杂的问题[22－23]。

根据特征建模思想，当要实现速度跟踪控制并保持与列车原动力学方程等价时，应先对列车系统的输入输出关系构建相对应的特征模型。由式（2）的模型结构，先将高速列车非线性模型简化为

式中：f（v，u）=ξ0+ξ1u+ξ2v+ξ3v2，ξ0=-γa，ξ1=γ，ξ2=-γb，ξ3=-γc。这些参数都是不确定的，随着列车运行工况的改变而改变。

根据文献[24]提出的由非线性系统推导建立对应的二阶等价时变差分方程形式的特征建模方法。本文由特征建模思想，对列车系统的输入输出关系构建离散形式的特征模型，取g0（k）u（k）作为输入，得到列车系统的特征模型

式中：u（k）和v（k）分别表示列车在k 时刻的牵引/制动力和运行速度，即高速列车在运行过程中系统的输入量为控制力，输出量为列车的运行速度；Δ0（k）为建模误差，由于u（k）在1 个采样周期内的变化量很小，所以此误差在小范围变化；f1（k），f2（k），g0（k）为待辨识的特征参数，可通过在线辨识得到，且参数的取值范围在有界范围内，即f1（k）∈（1，2]，f2（k）∈[-1，0），g0（k）≪1，g1（k）≪1。

1.3 列车特征模型参数辨识

在特征模型建立过程中，核心是特征参数的辨识，因而准确地在线实时辨识特征参数是十分重要的。针对上述建立的列车特征模型，本文采用递推最小二乘参数辨识方法对特征模型时变参数进行辨识。

其中：

式中：Φ（k）为列车系统输入输出向量，分别表示列车在k-1、k-2 时刻的速度以及系统的控制输入；θ（k）为特征模型时变系数向量，其中包含列车动力学中复杂高阶的有关信息，从而不至于丢失信息，且其参数估计值的范围与时变差分方程参数取值范围一致。为初值，其取值通常为零；K（k）为增益矩阵；P（k）为协方差矩阵，P（0）=（104～106）I，μ 为遗忘因子，当μ=1 时，则为基本的递推最小二乘法。

辨识后模型式（4）化为

1.4 存在系统误差的列车特征模型

通过将建模误差Δ0（k）和上述辨识误差看作总误差Δ（k），最后在式（6）的基础上得到存在系统误差的列车特征模型为

1.5 控制问题及控制目标

鉴于特征建模理论和扩张状态观测器的优势，考虑到列车系统由于系统误差产生的不确定性，本文针对上述所建立的存在系统误差的列车系统特征模型（7），通过结合扩张状态观测器对误差进行估计，以达到相应补偿的目的，设计自适应补偿控制器，由此实现存在系统误差情况下的高速列车速度跟踪控制。

因此，本文的控制目标为：针对存在系统误差的列车特征模型式（7），结合扩张状态观测器设计出基于特征模型的高速列车自适应误差补偿控制器u（k），保证速度跟踪误差在有限时间内有界，使列车在运行时的实际速度v（k）能渐近跟踪给定速度vd（k），即e（k）→0，其中e（k）=v（k）-vd（k），e（k）为速度跟踪误差。

本文设计的基于特征模型的高速列车自适应误差补偿控制框图如图1 所示。控制框图中主要包括控制器模块、递推最小二乘法辨识模块、控制器参数优化模块以及扩张状态观测器模块。控制器模块包括黄金分割控制、逻辑积分控制、逻辑微分控制，黄金分割控制是本方法中特有的一种反馈控制律。为了实现列车在存在未知系统误差的情况下对给定目标速度曲线的渐近跟踪，通过采用控制框图中的3 种控制器，结合扩张状态观测器，不断地对列车对象进行自适应调整，以获取较好的控制效果，使列车能够实时跟踪期望的速度。

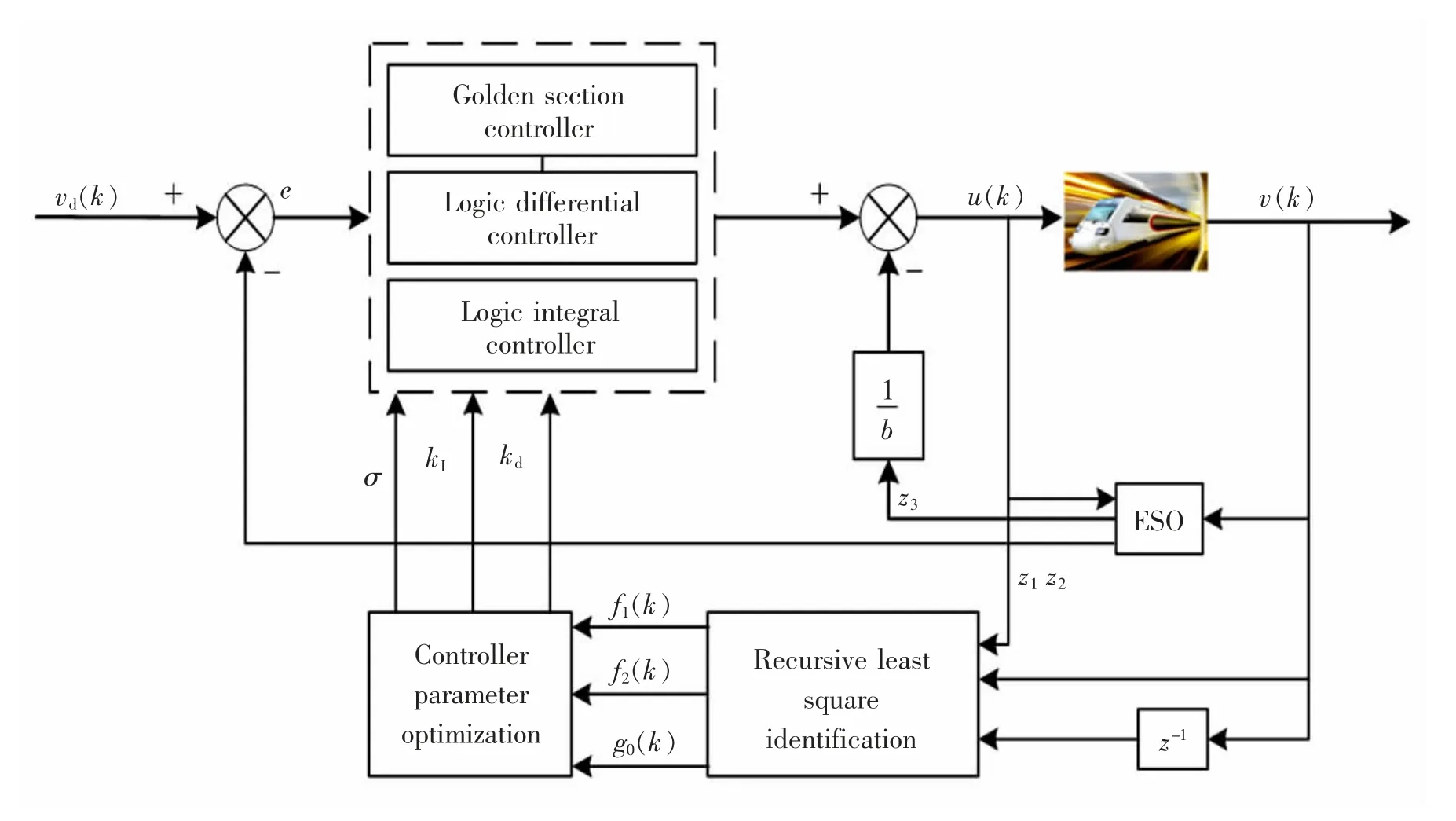
图1 高速列车自适应误差补偿控制框图Fig.1 Block diagram for adaptive error compensation control of high-speed train

2 列车自适应误差补偿控制器设计

基于控制目标，本文设计的控制器基本步骤如下：首先根据扩张状态观测器模块对系统误差进行实时估计；之后基于递推最小二乘法辨识得到的列车特征模型参数，设计基于特征模型的高速列车自适应误差补偿控制器；应用广义最小方差方法对控制器中的黄金分割控制、逻辑积分控制、逻辑微分控制中的参数进行优化，实现列车在存在系统误差情况下对给定目标曲线的渐近跟踪。

2.1 扩张状态观测器设计

根据上述控制框图，针对列车运行过程存在的系统误差，将其视为一个整体看作新的系统扩张状态，再结合采样得到的列车输入输出设计扩张状态观测器对其进行实时估计。

考虑到列车运行环境复杂多变，列车系统因不确定的运行状态和运行阻力等因素都会产生系统误差，将系统误差看作新的系统扩张状态，设该扩张状态为x3，对x3进行估计。在整个扩张状态观测器模块设计中，先令速度v=x1，加速度dv=x2，再分别对速度x1，加速度x2，系统误差x3进行观测，得到观测结果为z1，z2，z3。同时根据观测结果添加补偿量，对控制量进行补偿，并作用于列车系统。通过采样列车输入输出数据，利用扩张状态观测器对系统误差进行估计，便于设计相应的补偿，进而消除误差的影响，确保列车控制的精度。

通过上述分析，设计此扩张状态观测器为

式中：z1、z2和z3分别为速度v、加速度dv 和系统误差x3的观测值；b 为补偿因子，决定补偿量的大小；β1、β2和β3分别为观测器增益参数；fal（e，α，δ）为防振颤函数，主要用于抑制信号的抖震强度，具体结构为

式中：δ 决定防振颤函数中非线性区间的宽度。对上述参数进行合理的整定，可以使系统的性能得到改善。同时满足z1→x1，z2→x2，z3→x3的关系。

通过设计上述非线性扩张状态观测器，并对其中的参数进行合理的整定，以实现对被控对象的速度x1和加速度x2及系统误差x3的估计。为达到控制框图中对列车对象进行自适应调整的良好控制效果，将扩张状态观测器与基于特征模型的高速列车自适应控制相结合，构成最终的基于特征模型的高速列车自适应误差补偿控制器。

2.2 自适应误差补偿控制器设计

本节设计的基于特征模型的高速列车自适应控制器u0（k）由控制框图中黄金分割、逻辑积分、逻辑微分3 种控制量协同作用，采用广义最小方差方法对控制器参数进行优化，以减小调参复杂度。在此基础上，结合扩张状态观测器对系统误差的观测值，得到基于特征模型的高速列车自适应误差补偿控制器u（k），以取得更好的控制效果。

2.2.1 基于特征模型的自适应误差补偿控制器

为了实现列车在存在系统误差情况下对给定目标曲线的渐近跟踪，设计基于特征模型的高速列车自适应误差补偿控制器。针对存在系统误差的列车特征模型（7），根据2.1 中系统误差x3的观测值z3和基于特征模型的高速列车自适应控制器，设计基于特征模型的高速列车自适应误差补偿控制器为

式中：u0（k）为基于特征模型的高速列车自适应控制器；b 为补偿因子。该控制器通过基于特征模型的高速列车自适应控制器计算得到控制量u0（k），同时根据观测结果添加补偿量1/b，其目的是设计基于此不确定性观测的反馈控制，对控制量u0（k）进行补偿，将最终控制量u（k）再作用于列车对象，得到输出速度，使列车能够较好地跟踪期望速度值。

2.2.2 基于特征模型的高速列车自适应控制器

本文设计的CMGSID 控制方法（characteristic model-golden section-integral-differential control，CMGSID）是由黄金分割控制、逻辑积分控制、逻辑微分控制组合而成。此控制器u0（k）包括3 个部分，形式如下

式中：ug（k）为黄金分割控制器（Golden-section control）；ui（k）为逻辑积分控制器（Logic integral control）；ud（k）为逻辑微分控制器（Logic differential control）。

1）黄金分割自适应控制器。黄金分割控制能够保证闭环系统在参数估计未收敛到真值时是稳定的，其一般形式可表示为

式中：l1和l2分别为黄金分割比例系数，l1=0.382，l2=0.618；e（k-1）=v（k-1）-vd（k-1）即为在k-1 时刻列车期望速度减去列车实际速度的速度误差；，是参数估计值并且有界，σ 为可调参数。

2）逻辑积分控制器。逻辑积分控制可以消除非零均值干扰以及输出静态误差，其控制器形式为

式中：kI为积分系数，且ε 为一个较小的正数。

3）逻辑微分控制器。逻辑微分控制当系统进入稳态时，可以增大系统阻尼，减小震荡幅度，其控制器形式为

式中：kd为积分系数；N 为微分系数。

2.2.3 控制器参数优化

由于对上述控制器参数σ、kI和kd进行调整较为困难，本小节采用广义最小方差方法对控制器参数进行优化，以减小调参复杂度，取得更好的控制效果。首先将基于特征模型的高速列车自适应控制器输出表达式简化为

由于本文中的列车特征模型是单输入单输出系统，其受控自回归模型可以表示为

式中：

ζ（k）为零均值的白噪声序列，D 为延迟步数。以此分析列车运行过程的特征模型式(4)，将其改写为如下自回归模型式

之后设列车控制系统的目标函数为

式中：P（z-1）和Q（z-1）为加权多项式；R（z-1）为输入模型多项式。同时定义目标函数为广义输出误差的平方。

为了求出使目标函数取最小值时的控制律，引入丢番方程

C（z-1）P（z-1）=A（z-1）F（z-1）+z-DG（z-1）（19）

在引入丢番方程后，通过对目标函数中的加权多项式进行计算推导，可以得到广义最小方差控制律为

根据文献[25]中的方法对上述控制律进行了简化，最终可得到上式的增广式广义最小方差形式为

式中：n 为待定参数。

经过以上的推导，可以进一步将控制器输出表达式转变为其增量形式

对比上两式，同时根据由列车特征模型式改写的式（17），可以得到na=2，=1，D=1，=0。由于之前简化最小方差控制律时，取C（z-1）=P（z-1）=1，则将丢番方程重写为

从上式中可以得出

则可得优化后的基于特征模型的高速列车自适应误差补偿控制器参数如下

为了实现列车在存在系统误差情况下对给定目标曲线的渐近跟踪，设计了基于特征模型的高速列车自适应误差补偿控制器。该控制器由基于特征模型的高速列车自适应控制结合扩张状态观测器对系统误差的观测值组成，针对控制器参数σ，kI和kd采用广义最小方差方法进行优化，减小调参复杂度的同时，使列车能够较好地跟踪期望速度值。

2.3 稳定性分析

为了证明本文所提控制方法的稳定性，通过选取上述目标函数中P（z-1），R（z-1），Q（z-1）的一组多项式，针对列车特征模型求出其在该组目标函数下的广义最小方差控制律。由对比可知广义最小方差控制律与基于特征模型的黄金分割控制律相同，最后基于广义最小方差的收敛性和稳定性的结果得到黄金分割控制律的闭环性质。

针对广义最小方差控制目标函数和广义最小方差控制律，选择恰当的Q（z-1），配置文中广义最小方差控制律的B（z-1）+C（z-1）Q（z-1）为（n 为常数）。由此，本文的受控自回归模型可解得

按照最小二乘算法辨识上述参数θ（k），然后根据表达式设计控制律。根据文献[26]中的定理1 和2以及D=1 可得如下命题。

命题1[26](稳定性)对于上述算法，如果

式中：

则有

命题2[26]（收敛性）对于上述算法，如果σ（k）=0 则有

基于上述命题，由于广义最小方差控制律的稳定性和收敛性依赖于以下式的稳定性，则其闭环特征方程为

引理[26]若特征模型是非最小相位系统，当系统开环稳定时，则存在n＞0，使得式（26）稳定。

定理针对存在系统误差的列车特征模型式（7），所有信号都是有界的，设计基于特征模型的自适应误差补偿控制器（10），使得系统的跟踪误差是有界的，并且有sup|e（k）|≤σ。

证明将式（10）代入式（7）中，基于辨识得到的参数设计控制器，并通过引入广义最小方差对控制器参数进行优化，当基于广义最小方差的收敛性和稳定性的结果满足引理1 时，本文控制律的闭环稳定性质即为

进而可得

将n 看作根轨迹参数时，当开环稳定时其开环零点和开环极点均在单位圆内，根据根轨迹法和式（27）可知存在常数n＞0，且时变参数有界，使得系统稳定。再由上述两个命题以及引理1 可知误差e（k）有界，且sup|e（k）|≤σ。

3 仿真验证

为验证本文提出的建模和控制方法的效果，选用CRH380A 型高速列车作为研究对象进行仿真实验研究。选取该趟列车在济南—徐州东路段的实际运行数据作为实验数据，本文采用不同控制方法作了两部分的仿真。

第一部分利用本文设计的基于特征模型的高速列车自适应误差补偿控制方法对所建立模型进行速度跟踪控制，该控制器由黄金分割控制、逻辑积分控制、逻辑微分控制以及扩张状态观测器组合的控制器（CMGSID+ESO），并验证在受到误差影响下的本文方法的抗干扰性能；第二部分分别采用传统PID、基于特征模型的高速列车自适应（CMGSID）控制方法，使用相同目标跟踪曲线，在参数突变一致的情况下进行对比，比较3 种控制方法性能差异。

3.1 CMGSID+ESO 控制方法仿真效果

首先基于2.2 中调试的设计数据，并根据2.2中的设计内容，对运行在京沪高铁线路上的济南—徐州东的列车进行速度跟踪控制仿真实验。经过不断的调试，CMGSID+ESO 方法中控制器参数经优化后调试为n=5；以得到良好的控制性能为目标，根据经验值采用试凑法将ESO 参数设置为β1＝0.7，β2＝0.3，β3＝0.4，δ＝3.5，α1＝0.5，α2＝0.25。实验得到的仿真结果如图2 所示，分别为该方法对给定速度和位移的跟踪控制曲线。其中：yr表示目标速度曲线，Sr表示目标位移曲线。

通过对仿真结果进行分析，在速度跟踪的局部放大图中，本文控制方法得到的速度跟踪曲线能基本紧密的追踪上目标速度曲线yr，保持一定重合度。同时在位移跟踪的局部放大图中，本文控制方法得到的位移跟踪曲线也能较好地跟踪目标位移曲线Sr，表明本文控制方法能使列车在运行过程中具有较好的跟踪性能。

然后验证在受到误差影响下，CMGSID+ESO控制方法的抗干扰性能。本文设置当列车运行至t=1 495 s 时，设定相同的运行模型参数突变，持续时间为90 s，而后将该参数改回原值。本文控制方法下得到的高速列车速度跟踪曲线和速度误差曲线以及加速度跟踪曲线的仿真结果如图3 所示。

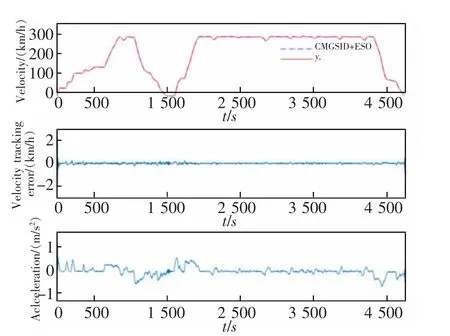
图3 CMGSID+ESO 仿真结果图Fig.3 CMGSID+ESO simulation results

通过对仿真结果进行分析，图3 中CMGSID 控制的速度跟踪误差和加速度曲线在突变时刻有轻微跃变，速度跟踪误差在[-0.261 1，0.270 2] km/h 范围内，CMGSID+ESO 控制方法得到的速度跟踪均方根误差为0.08 km/h。由于ESO 可以较快地观测系统误差并补偿，很快就能继续保持参数未突变时的跟踪，不再出现速度的急剧增减，且跳变幅度也较小。显示了本文控制方法的有效性。

本文控制方法下的特征参数和控制器参数受系统误差影响的变化曲线如图4 和图5 所示。

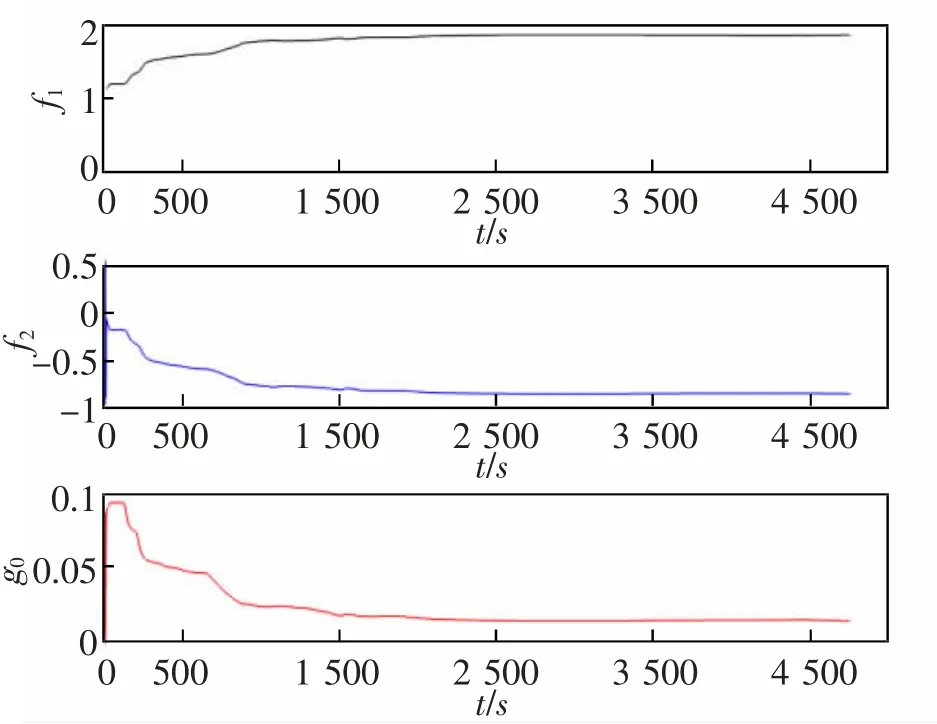
图4 特征参数曲线Fig.4 Characteristic parameter curves

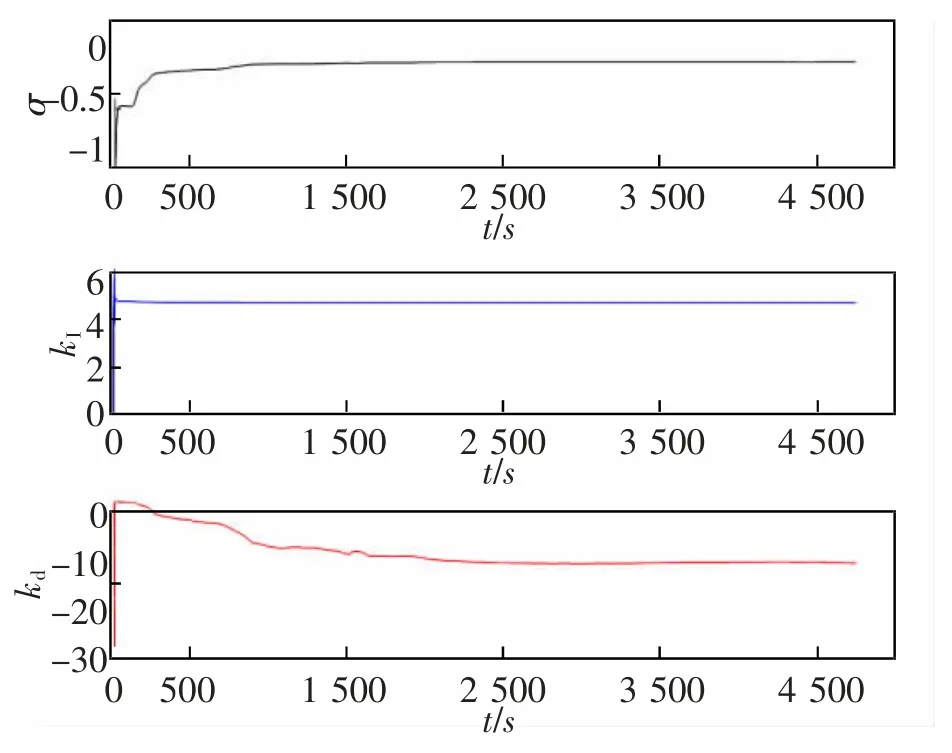
图5 控制参数曲线Fig.5 Control parameter curves

图4 表明，系统存在误差情况下，该参数变化曲线在1 500 s 后变化较为平滑，对特征参数f1（k）和f2（k）的影响较小，对g0（k）影响较大。图5 表明，在同样系统存在误差情况下，控制器参数kI变化曲线较为平滑，参数σ 变化曲线在500 s 后变化较为平滑，对参数λ 和kI的影响较小，对kd影响较大。特征参数和控制器参数受系统误差的整体影响较小，有效体现出本文控制方法具有较好的追踪性能和较强的自适应能力以及抗干扰性。

3.2 传统PID 和CMGSID 控制方法仿真效果

为了验证本文所设计的CMGSID+ESO 控制方法在抗干扰方面的优势，以下采用传统PID 控制和CMGSID 控制方法与本文的控制方法进行对比。经过不断的调试，传统PID 控制器参数可设为kp=3.7、kI=3、kd=2；CMGSID 方法中控制器参数经优化后调试为n=5。实验仿真了两种控制方法在存在系统误差情况下对于速度跟踪误差和加速度跟踪的跟踪效果，图6 是采用PID 控制算法的仿真结果，图7是采用CMGSID 控制方法的仿真结果。

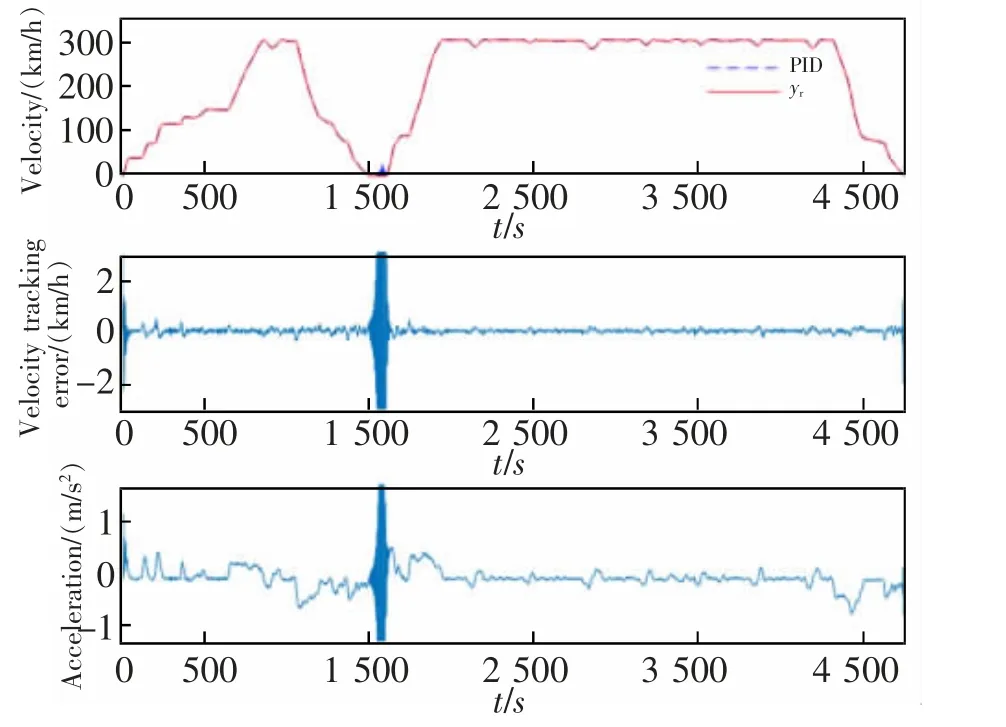
图6 PID 仿真结果图Fig.6 PID simulation results

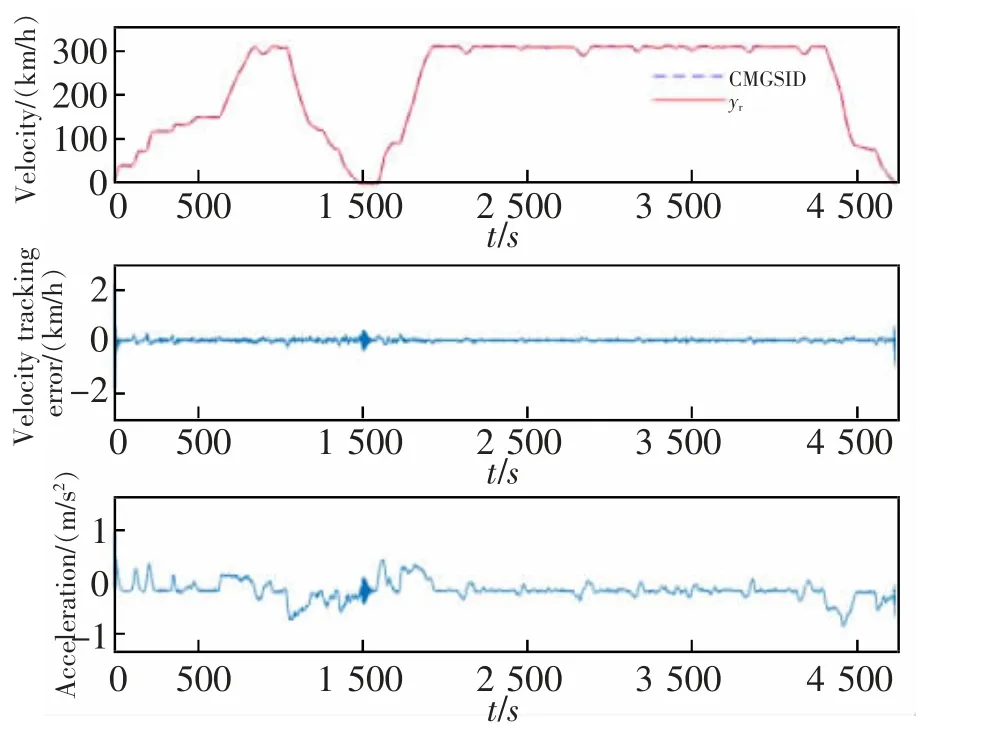
图7 CMGSID 仿真结果图Fig.7 CMGSID simulation results

通过对仿真结果进行分析，在速度跟踪方面，当列车运行至1 495～1 585 s 时，图6 中PID 控制的速度跟踪存在明显的跃变。同时，由PID、CMGSID两种控制方法得到的速度跟踪的均方根误差分别为：0.668 4，0.084 0 km/h。从仿真结果可以看出，在发生系统参数突变时，本文方法（CMGSID+ESO）能够对其进行有效处理，并且速度跟踪误差跳变幅度最小；CMGSID 控制方法能够较好地处理参数突变，该方法下的速度跟踪误差跳变幅度小于0.5 km/h；PID 控制方法在处理参数突变时其速度跟踪误差大于2 km/h。经对比可知本文设计的CMGSID+ESO的控制效果最好，CMGSID 控制次之，PID 控制最差。在速度误差方面，图6 中PID 控制下的跟踪误差曲线有一个波动较大的跳变，并且在高速列车初期启动以及末期制动的速度跟踪误差相对较大。图7 中CMGSID 作用下的跟踪误差曲线也产生了一定波动幅度，而本文控制方法下得到的跟踪误差有轻微跃变且后续依然可以保持平稳跟踪。在加速度跟踪方面，PID 和CMGSID 控制也在突变点均出现一定幅度的跳变。由加速度跟踪精度大小可以反映乘客舒适性指标，可以看出，PID 控制方法得到的加速度跟踪曲线在突变点出现较急剧变化现象，极易影响高速列车的安全运行和乘客的舒适性。

因此，相较于传统PID 控制和未加扩张观测器的CMGSID 控制方法，在受到系统误差影响下，本文方法得到的速度和加速度跟踪曲线能有效克服突变的影响，仍能实现对给定速度曲线的渐进跟踪，具有较好的抗干扰性和鲁棒性，同时提高了列车运行的控制精度。

4 结论

采用特征模型的方法，针对高速列车运行过程中因系统误差导致的不确定性等问题进行了研究，得出以下结论。

1）对于存在系统误差的高速列车运行过程，基于特征模型方法设计自适应误差补偿控制器，能保证系统稳定，实现对给定速度曲线的渐近跟踪，从而保障高速列车的安全可靠运行。

2）针对存在系统误差的高速列车特征模型，结合扩张状态观测器设计控制器，该控制器能够有效处理系统误差带来的不确定性，提高控制精度，具有良好的鲁棒性。

3）本文设计的控制系统考虑了系统误差带来的不确定性，提高了列车运行的控制精度，确保了高速列车安全可靠平稳运行。进一步考虑同时存在系统误差和扰动的高速列车自适应抗扰控制策略是下一步的研究方向。