基于轨迹数据的过饱和信号路口排队长度分析

刘旭星，邓明君，彭理群

（华东交通大学交通运输工程学院，江西 南昌 330013）

排队长度是信号控制交叉口运行状态的关键评价指标之一，也是信号控制优化的重要目标之一[1]。传统的周期最大排队长度估计研究主要依赖线圈、地磁等定点检测器采集的交通流信息，在交叉口处于过饱和情况下，排队车辆可能超过检测区域，形成长队列问题，此时难以用固定位置检测器来估计排队长度。

近年，随着移动互联、智能网联的快速发展，基于网联车车辆轨迹数据的交叉口排队长度估计得到国内外学者的广泛关注。利用车辆轨迹数据估计排队长度的方法主要分为两大类。一类是概率方法。谈超鹏等[2-3]利用历史轨迹推导经验非参数到达分布，提出了一种概率方法，将队列长度估计公式化为参数估计问题，并估计了周期中具有最大概率的排队长度。然而，该方法仅基于观测样本构建概率函数估计排队长度，在样本充足的高渗透率条件下可以得到较为可靠的估计，而低渗透率条件下则精度难以保证。在该研究基础上，谈超鹏等[4]又提出了一种抽样车辆轨迹数据的队列估计模型，无须假设特定的车辆到达、信号配时、交通量或排队特征等信息，不考虑渗透率的随机性，提高了模型的准确性和一致性。张伟斌等[5]基于贝叶斯定理推导出排队长度与联网车辆停车位置的概率关系，结合历史排队数据分析在高斯及非高斯情况下排队长度的置信区间估计，用概率分布偏差来描述排队长度。Zhang 等[6]采用期望最大法，根据交通状况对不同的到达分布进行建模，估计每个周期的到达率，然后根据冲击波理论估计队列末端和初始队列，该方法即使渗透率较低的情况下也可以产生精确的估计。Zhao 等[7]通过利用探测车在队列中的停车位置，建立并求解探测车渗透率的单变量方程，获得探测车辆渗透率，基于渗透率预测总队列长度和总交通量。Yu 等[8]提出了一种基于贝叶斯网络的随机学习方法，在渗透率低的情况下，也能达到相当好的精度。总的来说，现有的大部分基于概率方法估计交叉口排队长度的研究，需要假设车辆的到达分布已知，其实用性受到限制，尤其是在交通高峰时期交叉口出现过饱和的情况下，难以确保其精度及稳定性[9-10]。

另一类是基于车辆轨迹的方法。Liu 等[11]利用最近一个周期内的排队流量过程来解决交叉口排队长度的测量问题，但模型在过饱和状态下会有局限性。姚佼等[12]根据车辆在队列中的不同位置，分别建立了延误最小的最大排队长度估计模型。王爽等[13]提出了基于交通流历史时间序列的自相关分析，采用不同算法进行多输入步长的交通流预测。Rameazni等[14]利用车辆轨迹数据通过对排队过程和消散过程拟合，绘制排队轮廓曲线，达到排队长度估计的目的。王志建等[15]提出通过浮动车轨迹数据来估计信号交叉口的排队长度，在早晚高峰及平峰流量及不同渗透率的情况下估计排队长度。Li 等[16]通过对驾驶员进入交叉口前的行驶状态分析，将排队过程分成几个阶段，在前人的基础上提高了加入排队点和离开排队点的估计精准度，实现了排队长度更精准地估计。Tan 等[17]，羊钊等[18]通过交通冲击波理论分析排队的形成及消散过程，提出了一种最大广义排队长度估算模型。Yang 等[19-20]通过分析高精度车辆的车辆轨迹，提出一种基于阈值的临界点提取算法，确定车辆停车和启动的临界点，结合交通波理论计算车辆排队长度和延误。Osman 等[21]提出了一种基于冲击波的逐周期估计最大队列长度和初始队列的算法，定义了队列形成覆盖指数，并证明该指数对队列长度估计精度有显著影响，但没有考虑交叉口车辆溢出回流情况下的排队估计。Cai 等[22]融合点传感器和移动传感器观测到的探测车行驶轨迹，提出了基于交通冲击波理论的最大队列长度估计模型，该模型在交叉口欠饱和及过饱和的情况下均保证一定精度。Comert 等[23]提出了一种从配备距离测量传感器的连接车辆估计队列长度的方法，该方法适用于欠饱和及过饱和情况。然而，大多数研究未能充分考虑初始排队对周期排队长度估计的影响。基于上述问题，提出了一种基于冲击波理论的网联车车辆轨迹估计过饱和交叉口排队长度的方法。

1 问题描述与模型假设

1.1 问题描述

当城市交叉口出现交通过饱和状态时，车辆可能在进入交叉口后不能在一个绿灯周期时间内驶离交叉口而进行二次甚至多次排队。图1 表现了在交通不饱和的情况下车辆到达交叉口的分布，网联车1 和网联车2 均在一个信号周期到达交叉口；而在图2 中，在过饱和情况下，车辆进行多次排队，在道路队列中的车辆可能来自多个信号周期。出现过饱和情况时，周期开始时就可能存在车辆排队且车辆的到达分布及轨迹均与不饱和状态时不同。因此，对于不饱和状态交叉口的排队长度估计方法在过饱和情况将不再适用。针对这一问题，本研究的主要目标是解决过饱和信号交叉口逐周期的初始队列长度和最大排队长度估计问题。即通过对每个网联车车辆轨迹进行分析，识别出车辆行驶的临界点，运用交通冲击波理论对过饱和信号控制交叉口的初始队列长度和最大排队长度的估计进行了研究分析。

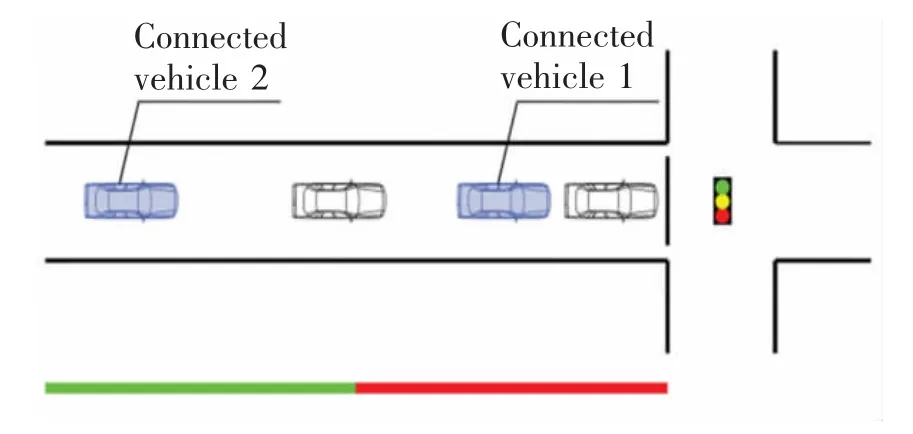
图1 欠饱和情况下车辆分布Fig.1 Distribution of vehicles under unsaturated conditions

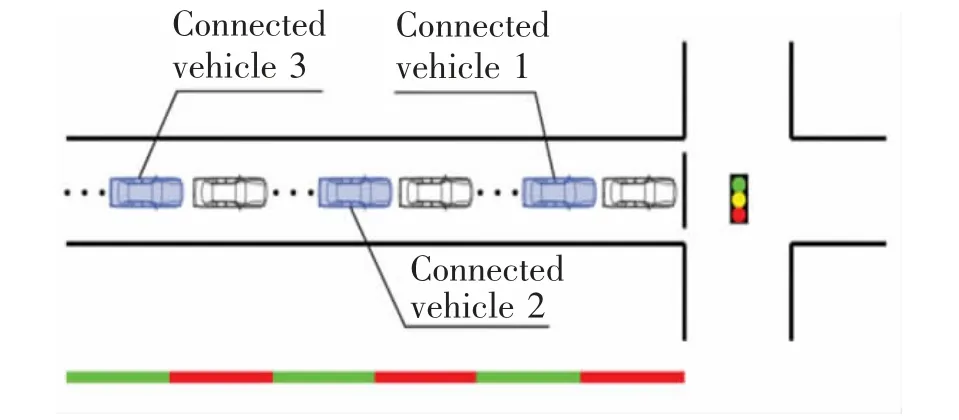
图2 过饱和情况下车辆分布Fig.2 Distribution of vehicles under oversaturation conditions

为了简化讨论，模型作出以下假设：

1）已知给定交叉口的信号配时；

2）一个周期中至少存在一辆网联车车辆轨迹，确保模型可用；

3）除在排队状态下，所有车辆都以自由流速度行驶；

4）若周期存在初始队列，则同一个阶段内交通冲击波波速u2与u4相等；

5）本研究仅以南北向直行车流进行实验，且不考虑车辆换道影响。

1.2 交通冲击波分析

在交叉口流量过饱和时，由于信号控制引起的车辆行驶状态变化，车辆排队经历“形成—消散—未完全消散—形成初始排队”过程，从而信号交叉口会产生多股交通冲击波。一般来说，可以用以下4个阶段来解释过饱和情况下车辆排队过程。

1）第1 阶段。当红灯起亮时，即周期开始时，到达车辆被迫停止。到达车辆和停止车辆之间形成排队累积冲击波w1，向交叉口上游传播。因此，在这一阶段，排队正在增加。

2）第2 阶段。在绿灯起亮时，排队的车辆开始以饱和流率排放，从而引发排队消散冲击波w2，其从排队的头部开始，并向交叉口的上游移动，冲击波w2的传播速度通常比w1快。

3）第3 阶段。一旦w1和w2相遇，就会形成一个向停车线移动的排队压缩冲击波w3。由于在过饱和情况下该周期结束时仍存在排队车辆，w3不能到达停车线。

4）第4 阶段。过饱和条件下，周期结束时存在初始队列，生成初始队列形成波w4，向上游移动，直到其与w3相遇，之后形成下一个周期的新排队波。

图3 说明了过饱和条件下的冲击波传播过程。图3 中Lmin为初始队列长度，Lmax为最大排队长度，Tr为红灯起亮时刻，Tg绿灯启亮时刻。排队累积冲击波和排队消散冲击波的速度可通过以下函数计算

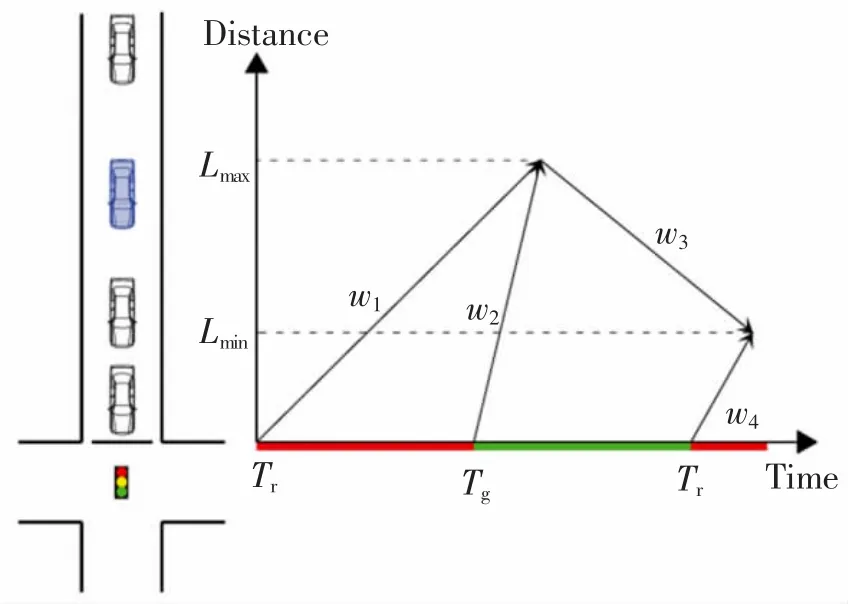
图3 冲击波产生原理及传播过程Fig.3 Shock wave generation principle and propagation process

式中：qa为到达率；ka为到达密度；qs为饱和流率；ks为相应的密度；kj为堵塞密度；u1，u2，u3，u4分别表示交通冲击波w1，w2，w3，w4的波速。

2 到达率分析

2.1 到达过程分析

为了利用所有排队的网联车轨迹，让Ui表示在一个周期内从每个停止的网联车轨迹中提取的信息

式中：ta（i）为第i 辆网联车到达的时刻；ts（i）为第i 辆网联车停止的时刻；to（i）为第i 辆网联车开始启动的时刻；td（i）为第i 辆网联车驶离停车线的时刻；li为第i辆网联车从停车线到其停车位置之间的距离；Na为周期内到达交叉口的网联车车辆数；Ne为周期内驶离交叉口的网联车车辆数。

交叉口在过饱和条件下运行，由于上一个周期中排队的车辆无法完全排出，因此在当前周期红灯起亮时可能会出现初始排队，此时初始排队中的网联车车辆在驶离交叉口前会出现二次排队的轨迹。如图4 所示，网联车在第n-1 个周期进入排队，并且在第n 个周期开始时属于初始排队。即一次排队车辆轨迹和二次排队车辆轨迹可以通过排队的网联车是否在第n-1 个周期结束时驶离交叉口来判断，如果网联车在第n-1 个周期结束时仍处于排队状态并且没有驶离，则在网联车驶离交叉口之前，将会经历二次排队。

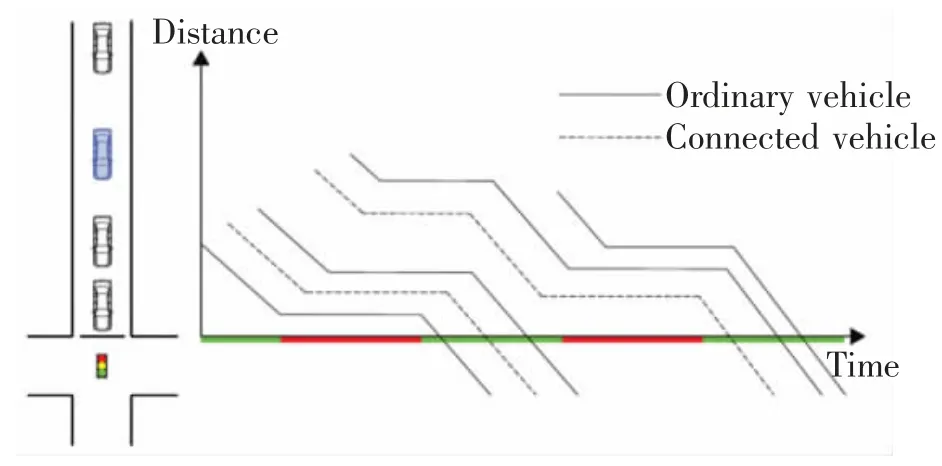
图4 过饱和交叉口车辆轨迹Fig.4 Vehicle trajectory at oversaturated intersections

2.2 到达率估计

根据一个信号周期内观测到的网联车车辆轨迹，可以分为仅观测到一辆网联车车辆轨迹和观测到多辆网联车车辆轨迹，并分别对其到达率进行估计。

当周期中观察到的轨迹数据中只有一辆网联车轨迹时，可以使用其停车位置到停车线之间的距离li来估计该网联车车前排队的车辆数量Nn。为了仅考虑在当前信号周期内到达的车辆，需减去周期开始时存在的初始队列中的车辆数。

式中：Nn为第n 个信号周期期间网联车前排队的车辆数；为第n 个周期初始队列中的车辆数量。在计算出Nn后，则可通过（4）式计算到达率

式中：Ta（i）为初始队列完全形成的时刻到第i 辆网联车的停车时间ts（i）之间的时间差；hj为饱和间距。其中Ta（i）计算式如下

如果在信号周期内观测到多辆网联车车辆轨迹（图5），则将其到达率计算为第i 辆网联车与第i+1 辆网联车之间到达率的平均值，如式（6）所示。

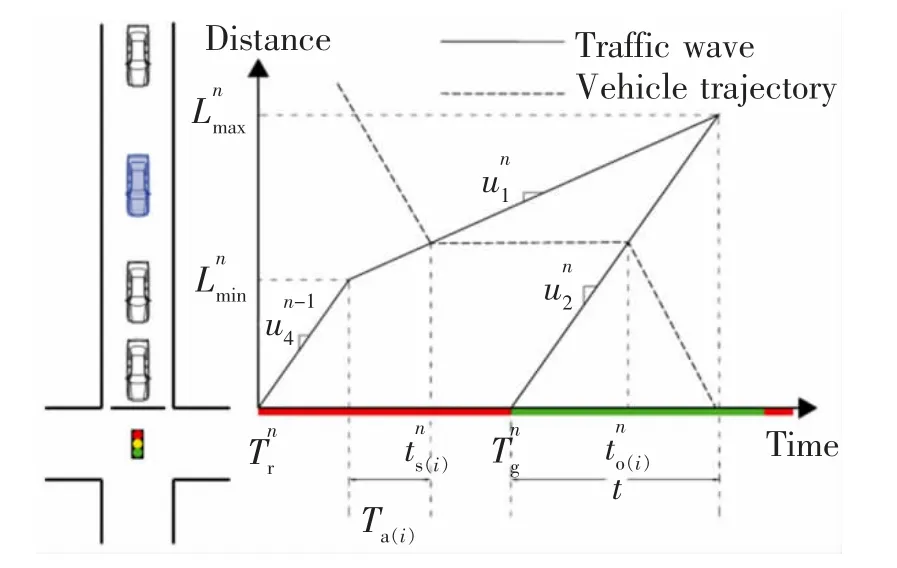
图5 排队过程示意图Fig.5 Schematic diagram of the queuing process

式中：Na为一个周期中网联车的车辆数。

通过上述得到到达率后，则使用基本交通流关系来计算相关的交通密度

2.3 饱和流率估计

根据网联车是在信号周期期间驶离信号交叉口还是作为下一周期初始队列分情况计算饱和流率qs。如果网联车在信号周期内未驶离交叉口并进行了二次排队，则参考HCM2000 假设此时饱和流率为1 800 pcu[21]；如果网联车在信号周期内驶离交叉口，则使用网联车驶离交叉口的轨迹信息估计信号周期绿灯时间内驶离交叉口的车辆总数，此时qs可计算为

式中：Nl为网联车前方驶离停车线的车辆数量，Nl＝Nn＋；td（i）为第n 个周期第i 辆网联车驶离停车线的时间；Tgn第n 个周期绿灯起亮的时间。

如果在信号周期绿灯时间内有多辆网联车驶离交叉口，此时qs计算为第i 辆网联车和第i+1 辆网联车饱和流率的平均值。

式中：Ne为一个周期内驶离交叉口的网联车车辆数。

3 排队长度估计

3.1 初始队列长度估计

为了估计初始队列长度，需要结合上一信号周期的最大排队长度和网联车轨迹。根据当前信号周期和上一信号周期的网联车轨迹类型，可以使用不同的方法估计初始队列长度。

如果在信号周期中只观测到一次排队的网联车轨迹而未观测到二次排队的网联车轨迹，如图6所示，在这种情况下需先判断当前信号周期是否存在初始队列。

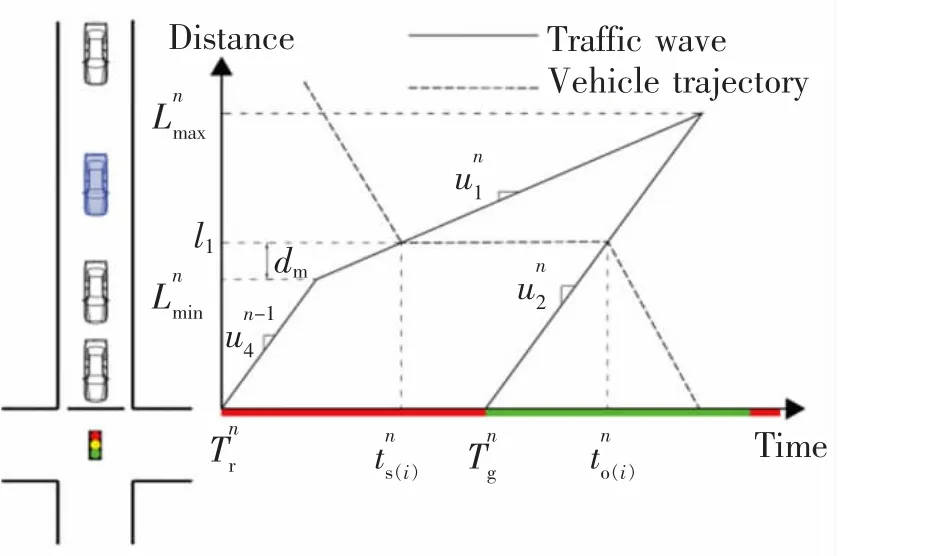
图6 周期只存在一次排队的网联车Fig.6 Only one-time queuing of connected vehicles in the cycle

根据信号周期第一辆一次排队网联车的轨迹数据，首先计算从初始队列长度末端到第一辆一次排队网联车排队位置l1之间的距离dm，并与l1进行比较。基于图6 的几何形状，距离dm通过以下公式计算

式中：l1周期第一辆一次排队网联车停车位置dm与l1停车线之间的距离。将距离dm与l1进行比较，如果dm=l1，则判断初始队列不存在；否则该信号周期中存在初始队列且其值计算为l1和dm之间的差值

如果观测到两辆及以上网联车在信号周期内到达，则到达率通过式（6）估计计算；当信号周期只观测到一辆网联车到达轨迹时，此时计算到达率应先计算初始队列中的车辆数量，如式（4）所示。然而，在式（10）中，要求已知到达率，这意味着及在计算中相互依赖。对于该特定的情况，基于图6中的冲击波三角形计算作为dm的函数，以求解两个方程并估计两个参数。这在数学上表示为

如果在信号周期中观测到二次排队的网联车车辆轨迹时，说明此周期中存在初始排队，如图7 所示。这种情况下初始队列长度可以基于上一周期绿灯时间内驶离交叉口的车辆数量进行估计。其中可通过以下公式计算

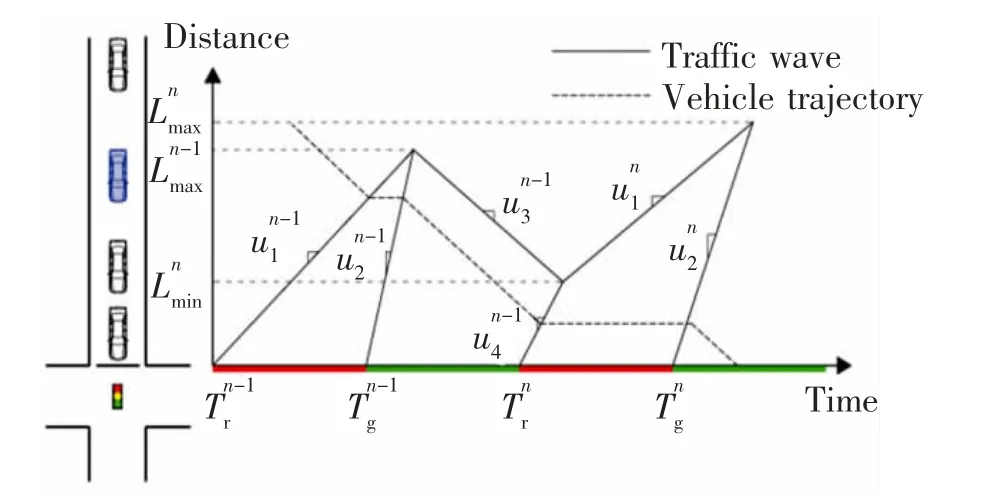
图7 周期存在二次排队的网联车Fig.7 Twice queuing of connected vehicles in the cycle

式中：lx为网联车车辆x 停车位置与停车线之间的距离。如果nx>，则使用式（14）计算初始队列车辆数；如果nx≤，此时初始队列内的车辆数量计算为

然后初始队列长度可以计算为

当交叉口下游车辆发生溢出回流时，由于回流堵塞，在信号绿灯期间不会出现车辆流出，在这种极端情况下，应首先利用网联车轨迹检测溢出的发生。如图8 所示，部分车辆在周期1 和周期2 驶入交叉口，在进行排队后一直保持静止状态，直到周期3 启动并驶离交叉口，因此可以相应地检测到周期1 和周期2 期间下游发生的溢出情况。

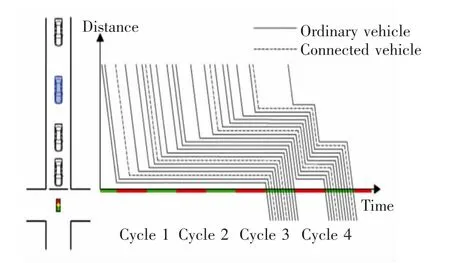
图8 溢出回流期间的车辆轨迹Fig.8 Vehicle trajectory during spillback cycles

如图9 所示，对于溢出回流信号周期期间的初始队列长度估计，由于没有车辆离开，可通过以下公式进行计算

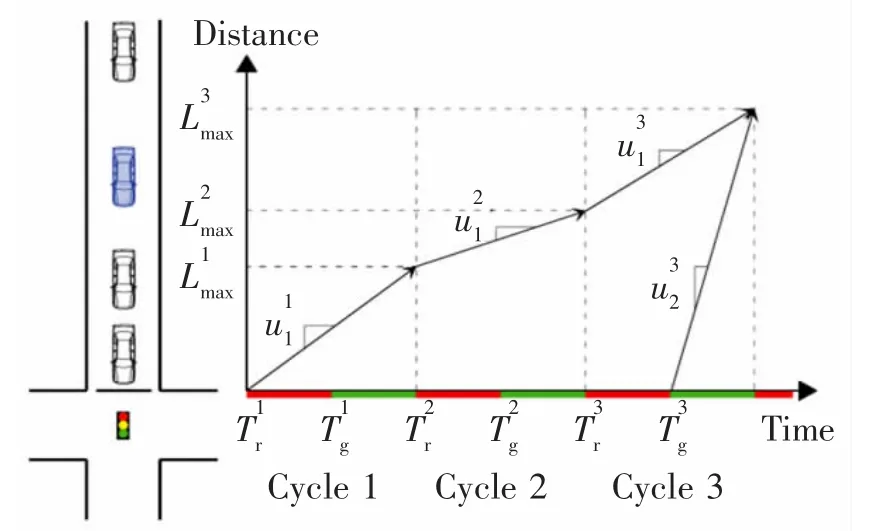
图9 溢出回流期间交通冲击波示意图Fig.9 Schematic diagram of a traffic shock wave during spillback cycles

3.2 最大排队长度估计

若信号周期中存在初始队列，如图5 所示，则使用下式来估计周期结束时的队列长度，最大排队长度估计为

式中：t 表示从绿色起亮时刻到队列达到最大长度时的时间。时间t 计算为

对于溢出回流信号周期期间的最大排队长度估计，如图9 所示，由于没有车辆离开，排队消散冲击波的速度等于0，而排队累积冲击波一直传播到信号周期结束。在这种情况下，可通过以下公式估算溢出周期的最大排队长度

4 实验分析

4.1 场景设置

仿真案例以南昌市八一大道—中山路交叉口为背景建立SUMO 微观仿真模型，研究对象为北进口的3 条直行车道，如图10 所示。信号配时采用定时控制，周期时长为134 s，有效绿灯时间为70 s。为了还原真实的交通场景，仿真模型利用实地调查采集的交通流量、转向比例等数据进行标定，数据采集时间为2017 年5 月8 日17:00—19:00 的交通高峰时段。

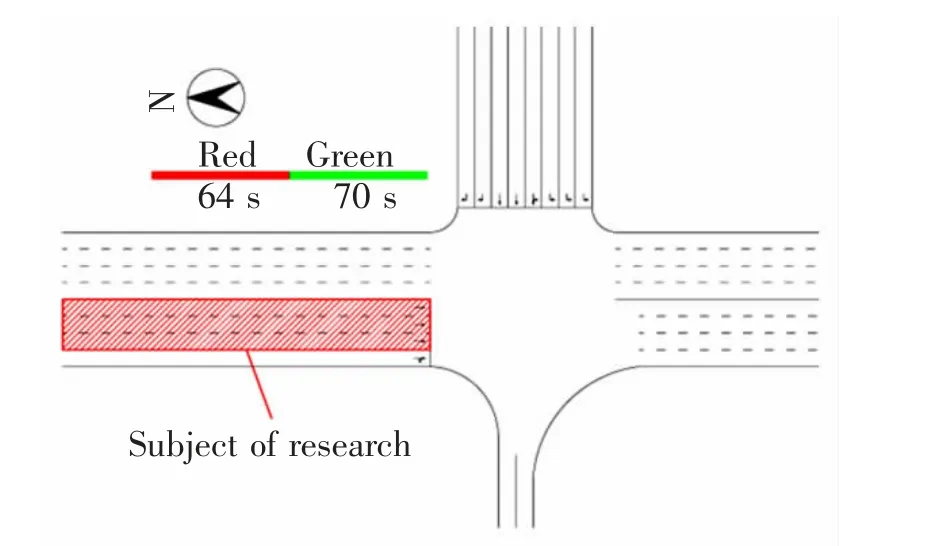
图10 仿真交叉口结构设计Fig.10 Design of intersection structure simulating

将调查的交通数据输入到SUMO 已建立好的目标交叉口仿真环境，按照每5 min 时间间隔对排队长度输出结果误差作校验，评价仿真交叉口建立的合理性。选取交叉口北进口道17:30—17:35 仿真输出的排队长度与实测排队长度进行对比分析，分析结果如表1 所示。

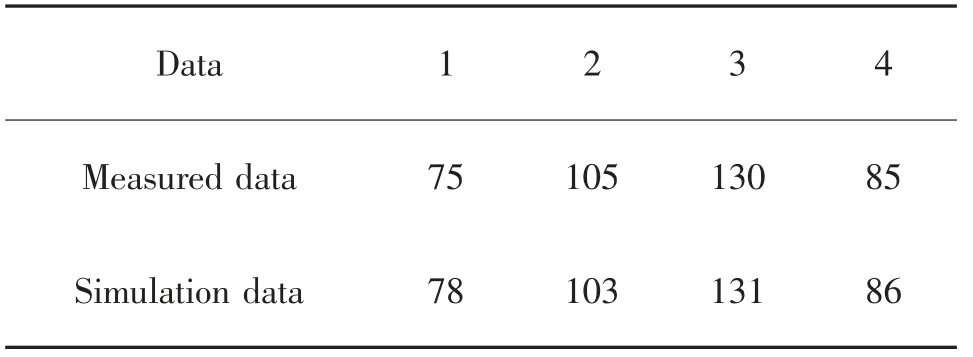
表1 高峰小时交叉口实测与仿真排队长度Tab.1 Peak hour intersection measurement and simulation queue length

由表1 可以看出，交叉口排队长度仿真值与实测值十分接近，且交叉口排队长度实测值均是以5 m 为最小度量进行采集和统计的，且道路交通流本身存在很大的随机性，所以仿真模型整体应用导致的误差可以接受。

为了进一步测试方法对不同参数的灵敏度，以实地调查的流量数据为依据，通过增大输入流量生成饱和度（v/c）为0.8 和1.0 的场景（v 为实际交通流量，c 为道路通行能力）；网联车渗透率设置为5%、10%、15%、20%、30%、40%及50%。在仿真实验中，仿真时长为3 600 s，包括300 s 预热时间及3 000 s有效时间。此外，为模拟车联网环境，仿真环境中每辆车都可实时获取位置、速度等信息，当周期内没有网联车车辆时，则随机抽取一辆车作为网联车，即使用其轨迹信息作为排队长度估计输入。此外，仿真设定车辆平均停车车头间距取7 m。

4.2 性能指标

为了评估排队长度的估计精度，选取平均绝对误差值（mean absolute error，MAE）和平均相对百分误差值（mean absolute percentage error，MAPE）作为评价指标，计算如下

式中：Li为第i 个周期的真实排队长度；Li为相应的估计值；Y 为评估的周期数；IMAE、IMAPE分别表示MAE、MAPE 的计算参数。

4.3 仿真结果与分析

通过仿真实验数据，获得交叉口各个周期的排队长度数据；同时，采用所提出模型对排队长度进行估计。在不同渗透率和交叉口饱和度（v/c）情况下，交叉口的排队长度估计值与仿真值的对比结果如图11 所示。

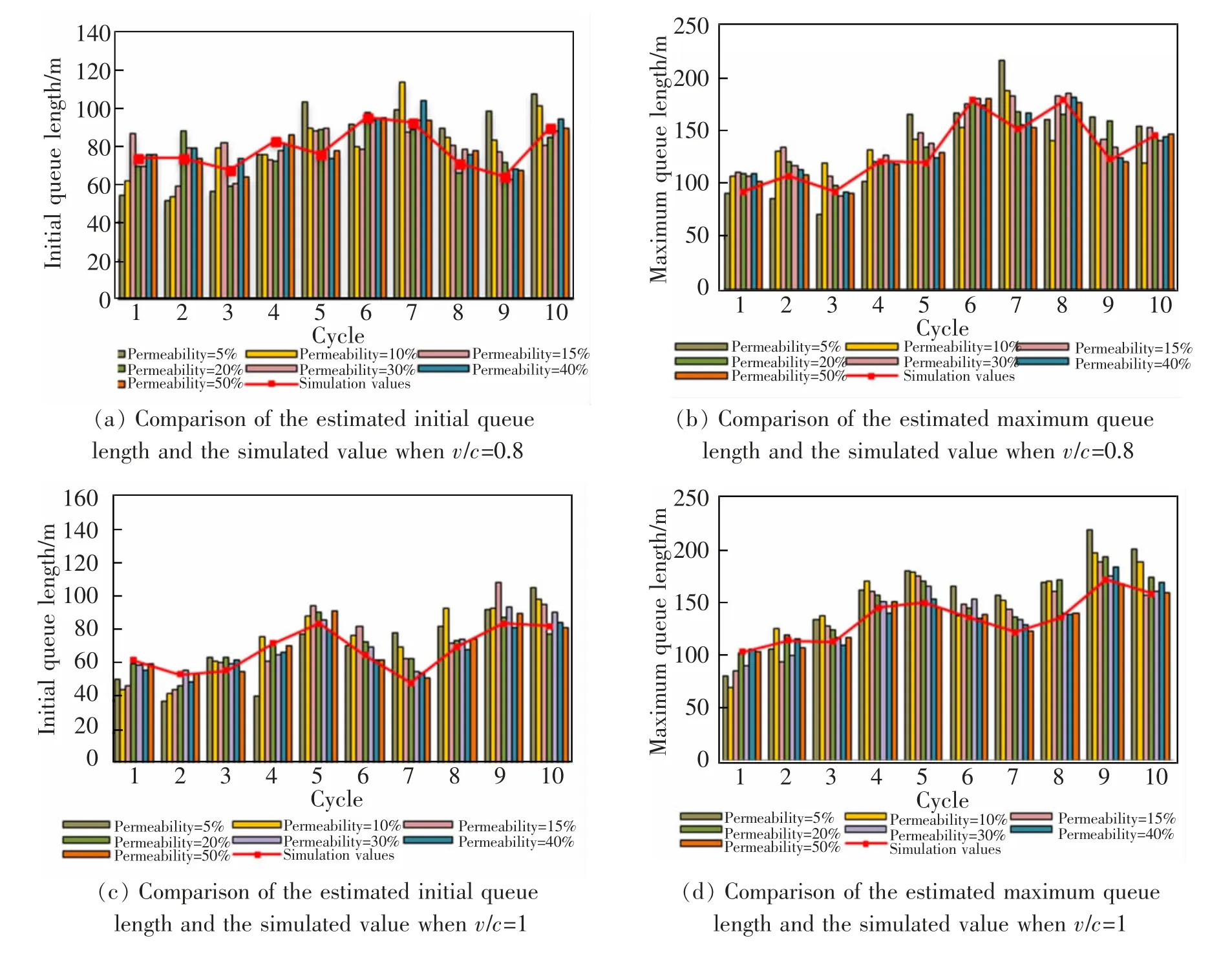
图11 不同饱和度及渗透率下排队长度估计值及仿真值对比Fig.11 Comparison of queue length estimation and simulation value under different saturation and permeability

为更好地评估模型性能，计算所有仿真实验结果的评价指标。不同场景下的仿真实验结果的IMAE、IMAPE及平均值如表2、表3 所示。在20%渗透率下，当v/c=0.8 时，初始队列长度和最大排队长度的IMAE分别为7.35 m 和12.18 m，IMAPE分别为9.79%和10.01%；当v/c=1.0 时，初始队列长度和最大排队长度的IMAE分别为6.28 m 和15.52 m，IMAPE均在10%左右。在10%渗透率下，当v/c=0.8 时，初始队列长度和最大排队长度的IMAE分别为14.54 m 和24.10 m；当v/c=1.0 时，初始队列长度和最大排队长度的IMAE分别为13.30 m 和26.06 m，IMAPE均不超过20%。在50%渗透率下，当v/c=0.8 时，初始队列长度和最大排队长度的IMAE分别为2.46 m 和3.43 m，IMAPE均不超过4%；当v/c=1.0 时，初始队列长度和最大排队长度的IMAE分别为3.01 m 和2.81 m，IMAPE分别为4.03%和2.81%。可知，在网联车车辆渗透率相同的情况下，随着饱和度的增加，模型的估计误差略微增大。

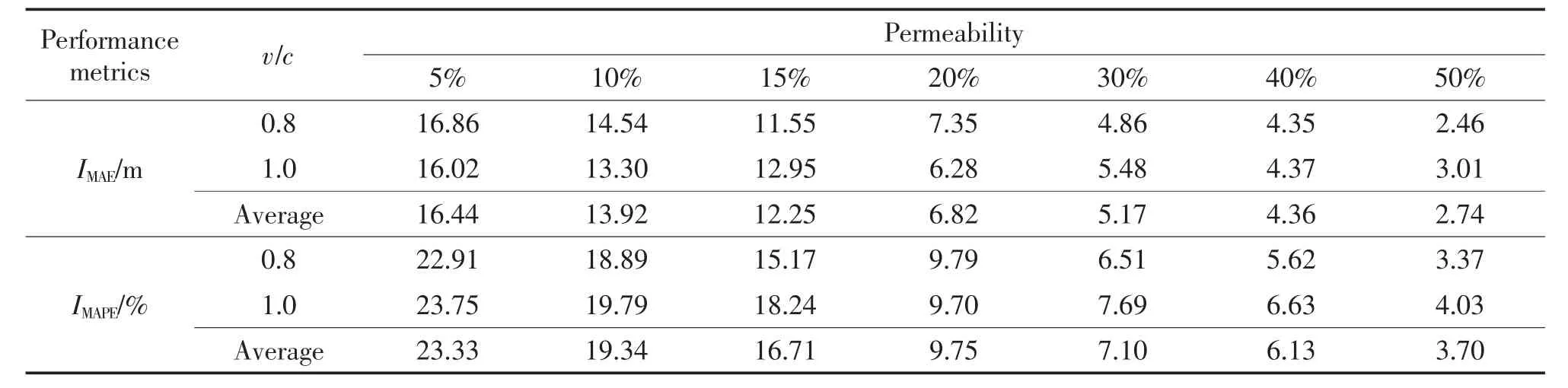
表2 不同渗透率下初始队列长度估计性能Tab.2 Estimated performance of initial queue length with different permeability

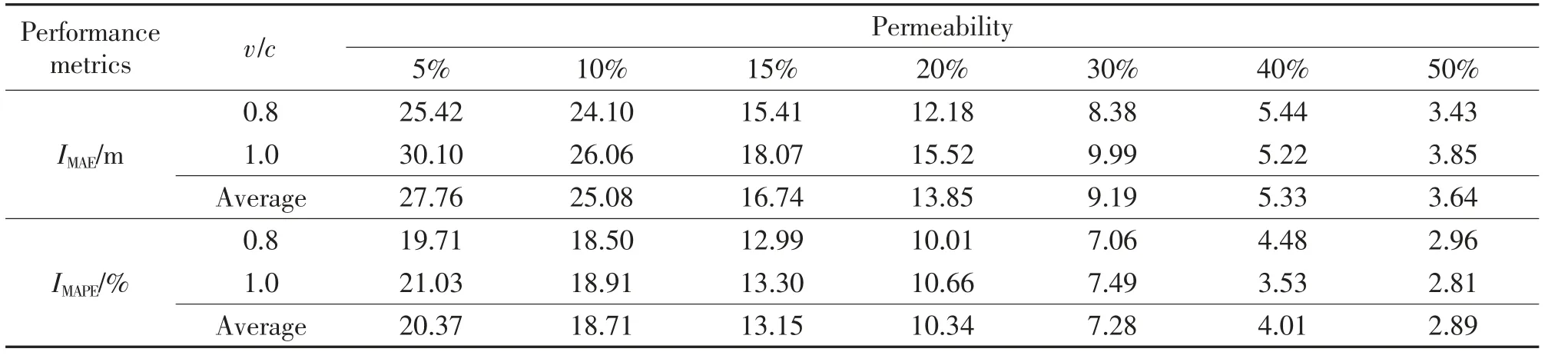
表3 不同渗透率下最大排队长度估计性能Tab.3 Maximum queue length estimation performance with different permeability

在网联车渗透率不低于20%的情况下，当v/c=0.8 时，初始队列长度IMAE小于7.5 m，IMAPE小于10%，最大排队长度的IMAE小于12.5 m，IMAPE小于10.5%；当v/c=1.0 时，初始队列长度IMAE小于6.5 m，IMAPE小于10%，最大排队长度的IMAE小于16.0 m，IMAPE小于11.0%。结果表明，在交叉口处于过饱和的情况下，模型依旧能够获得较好的估计结果。不同饱和度及渗透率的估计误差如图12，图13所示。

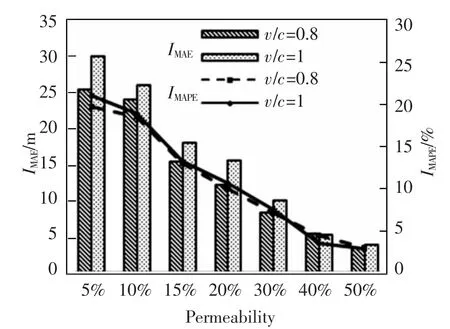
图13 不同饱和度及渗透率下最大排队长度的估计误差Fig.13 Estimation error of the maximum queue length with different saturations and permeability

由图12 可知，随着渗透率增加，初始队列长度估计误差指标均逐渐减小；在渗透率达到20%时，2个误差指标均有明显的下降。当渗透率为10%时，即可保证IMAPE小于20%。由图13 可知，在渗透率达到15%时，最大排队长度2 个误差指标有明显的下降，且可确保IMAPE在20%以内，说明模型在渗透率较低时仍有较好的估计效果。

5 结论

基于网联车车辆轨迹提出了逐周期的过饱和交叉口排队长度估计方法。首先根据网联车车辆轨迹上确定4 个临界点，标志着车辆到达和驶离信号交叉口期间的速度和位置变化，利用临界点信息估计到达率、交通密度和饱和流率。然后使用交通冲击波估计每个周期结束时的最大排队长度和下一周期初始队列长度。使用微观模拟器SUMO 在不同饱和度及渗透率情况下，对所提算法进行了测试。实验结果表明，该算法具有良好的性能，在交通过饱和的情况下，模型估计的排队长度误差也可以达到理想效果。结论如下。

1）所提出的方法是一种基于周期的初始队列长度及最大排队长度估计方法，这意味着所提出的方法在每个周期结束时估计最大排队长度及下一周期初始队列长度。因此，该算法不是实时的，后期可加强短时预测研究。

2）该方法要求每个周期至少有一辆网联车轨迹数据，在没有网联车的情况下方法不适用。下一步可以结合历史网联车轨迹数据，完善本方法在无网联车到达条件下的排队估计。

3）该方法不适用于直行和转弯混合车道的排队估计。下一步可以将该方法扩展到混合车道的排队长度估计。