宽幅钢箱梁顶推局部受力分析与控制
王 达,张志勇,黄 伟,谭本坤,向胜涛,赵鹏鑫
(1.长沙理工大学 土木工程学院,湖南 长沙 410114;2.中南林业科技大学 土木工程学院,湖南 长沙 410114;3.浙江省建投交通基础建设集团有限公司,浙江 杭州 310000)
综上,目前针对宽幅钢箱梁顶推过程中支承区域的钢梁局部应力过大的问题,通过局部构造对钢梁本身进行加固的研究较少。笔者以中卫卫民黄河大桥主拱钢箱梁顶推为施工背景,对顶推施工过程中的钢梁局部受力特性进行分析,探讨影响钢箱梁受力状态的主要构件参数,提出对钢梁局部构造进行加固的措施,以期确保顶推施工的安全可靠性。
1 工程概况
该桥上部结构为跨径布置100 m+130 m+40 m中承式梁拱组合体系,桥型布置图如图1所示。主梁为等高度钢-混凝土混合梁,箱梁横截面中线处梁高为4.5 m,顶面1.5%的双向横坡,钢箱梁为单箱三室断面,顶宽41 m,底宽34 m,挑臂长3.5 m,标准梁段顶板、底板、腹板厚度均为16 mm,所用钢材为Q345D,为了满足成桥线形,钢箱梁制造加工中设置了变曲率预拱度,钢箱梁横断面及支承位置如图2所示。主副拱区钢箱梁均采用步履式顶推法施工,顶推总长度约为40 m+131 m,以主拱区钢箱顶推过程为主,副拱钢箱梁顶推施工可参考主拱钢箱梁,顶推总质量约为3 144.5 t。主拱钢箱梁顶推施工主要步骤如下:首先采用履带吊将步履式顶推设备安放在临时墩上;然后在顶推平台上分阶段吊装并焊接好钢导梁、顶推梁段节段;最后由顶推设备的水平千斤顶和顶升千斤顶协同工作将钢箱梁整体顶推至设计位置处。用于主拱钢箱梁顶推过程的临时墩设置12个,最大跨度为26.6 m,顶推长度为131 m,主梁前端过9号临时墩6.25 m为顶推施工完成状态。主拱钢箱梁共有8种梁段类型,具体如表1所示。主拱钢箱梁顶推施工临时墩和顶推平台布置如图3所示。
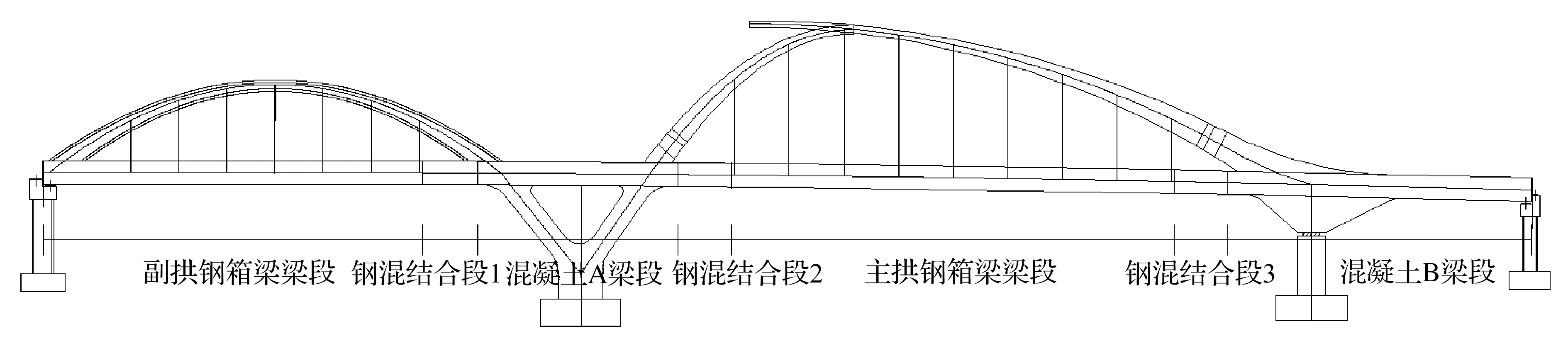
图1 桥型布置图

图2 钢梁横截面及支承位置图(单位:mm)

图3 主拱钢箱梁顶推施工立面布置图(单位:mm)
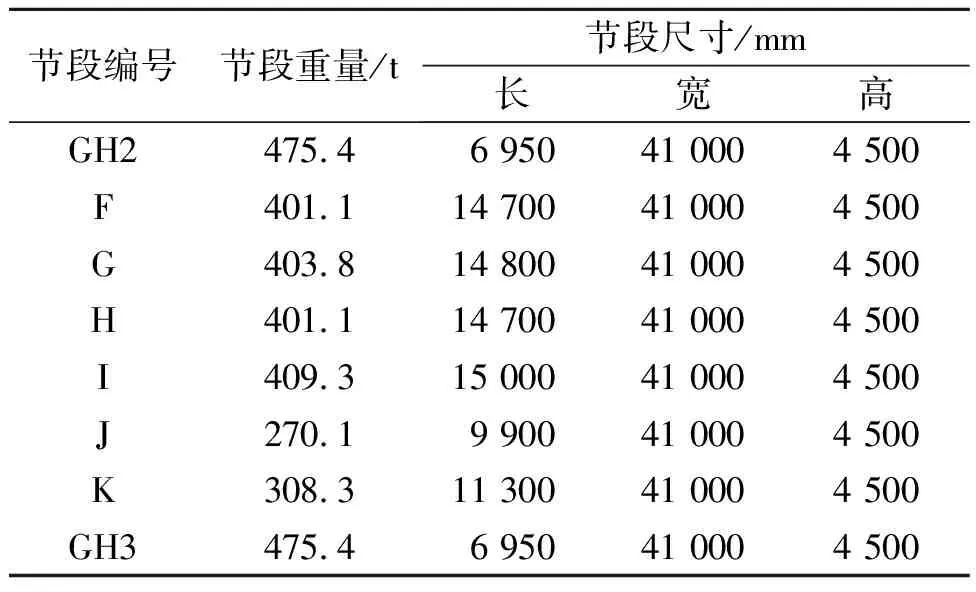
表1 梁段划分表
2 结构有限元分析
2.1 有限元整体分析
2.1.1 建立顶推整体模型
基于桥梁专用软件Midas/Civil建立主拱钢箱梁顶推整体模型,两根横向钢导梁简化为一根,对导梁的弹性模量E放大至原来的两倍,采用空间梁单元对钢箱梁、钢导梁进行模拟[11]。计算模型如图4所示。为了提高有限元模型的计算精度,以纵桥向每顶进0.5 m作为一个计算步长,采用“墩动梁不动”思想,顶推过程中对钢箱梁的约束采用弹性连接的“仅受压”,通过改变支承条件来模拟步履式顶推施工全过程。

图4 顶推计算模型
2.1.2 典型不利工况确定
通过顶推施工仿真分析,顶推过程中临时墩的最大支反力结果如表2所示。由表2可知:导梁即将上9号临时墩时,8号临时墩出现最大支反力为10 386.5 kN(支反力指的是钢箱梁梁底两侧垫块处的支承反力的总和),此时导梁下挠值也达到最大为-50.9 mm(挠度向上为正,向下为负)。对于钢箱梁桥截面来说,抵抗正负弯矩能力基本相同,而顶推施工过程一般负弯矩值比较大,顶推过程中负弯矩包络图如图5所示(截面位置表示该处至前导梁前端的距离),可得截面26 m处出现最大负弯矩,为-33 022 kN·m,所对应的顶推距离为107 m(即为发生最大支反力的工况),因此确定该工况为典型不利工况。由于在最大悬臂工况下8号临时墩所受的支反力过大,所在支承处附近的局部钢箱梁可能出现受力状态不稳定的情况,因此对该工况钢箱梁的局部受力进行精细化分析。
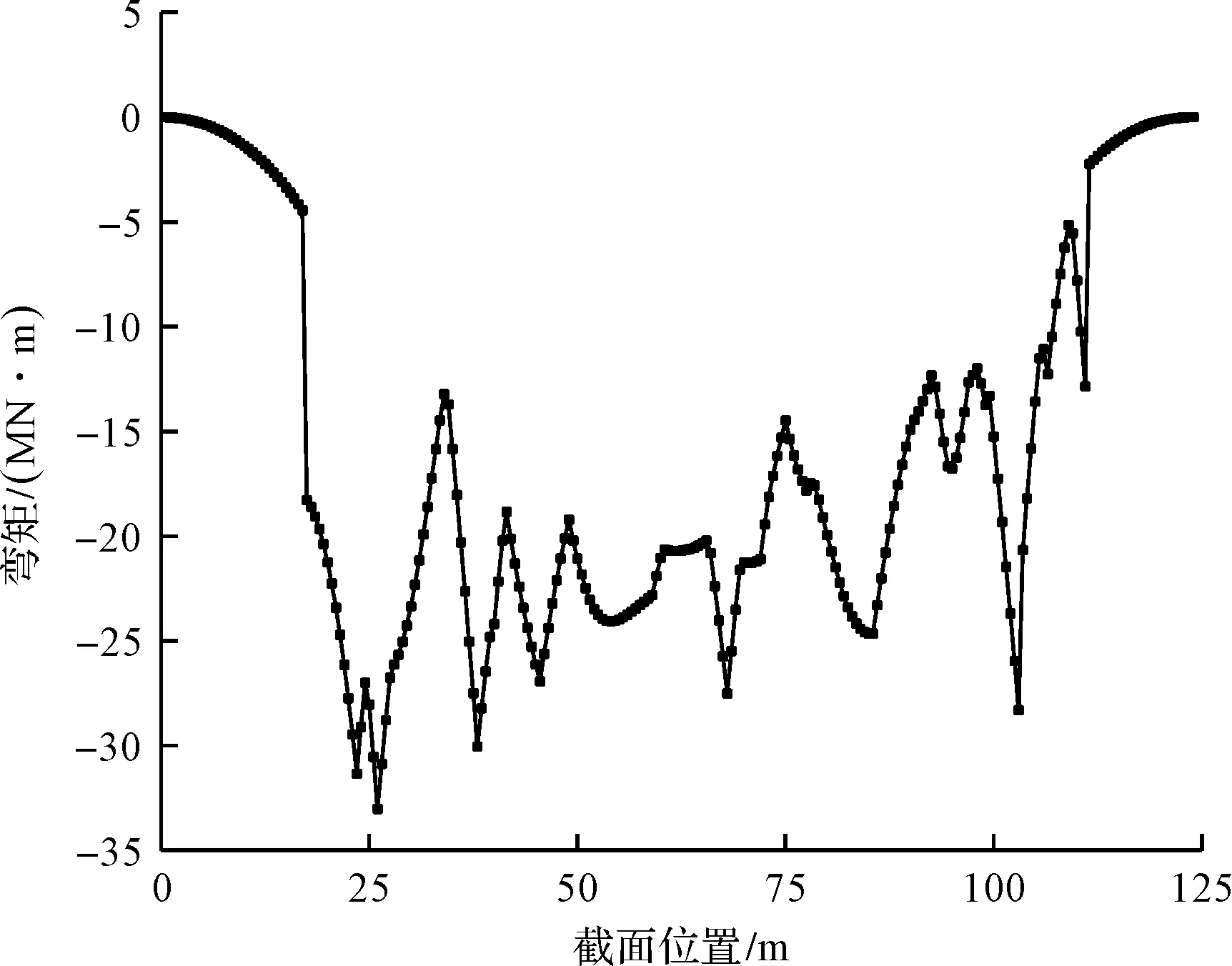
图5 顶推过程中负弯矩包络图

表2 顶推全过程最大支反力
2.2 有限元局部分析
在顶推过程中,垫块处上方的底板,腹板等板件局部应力变化极为复杂,箱梁又属于薄壁结构,极容易发生失稳,故采用有限元方法对支承区域的钢梁梁体进行局部受力分析。由Midas/Civil有限元分析软件建立的主拱钢箱梁顶推模型结果显示典型不利工况发生在导梁即将上9号墩时,最大支反力发生在8号临时墩上。局部模型的大小直接影响局部分析结果的准确性,根据文献[12],局部计算模型顺桥向长度应取梁高的3.0~4.5倍,取8号墩附近14.7 m钢箱进行局部受力重点分析。
首先使用乙醚将实验大鼠麻醉,选定胸正中为手术区域,去毛备皮消毒,做好关闭胸腔的荷包缝合准备,之后沿锁骨正中线做2 cm纵向切口切开皮肤,在第四或第五肋间将大鼠胸部肌肉进行钝性分离,使胸骨、肋骨充分暴露,将胸腔打开,心包剪开,在胸廓轻轻按压以将大鼠心脏挤出。使用无创性缝合线在动脉圆锥与左心耳之间冠状静脉处进行冠状动脉的结扎,之后将心脏迅速放回原位,将胸腔气体挤出,并迅速将缝合线拉紧,将胸腔逐层进行关闭,将外皮缝合好,保证开胸时间<60 s。
2.2.1 结构局部有限元模型建立
1)模型单元的选取。为了准确模拟出局部受力特性并降低对计算机性能的要求,基于有限元分析软件ABAQUS建立梁-壳-实-接触混合模型如图6所示,其基本原理是在结构整体模型的基础上,对所关注部位的局部结构进行精细化分析,并分析其应力分布的规律[13]。采用线性减缩积分单元S3R,S4R来模拟关注的钢箱梁部位,采用线性单元B31来模拟其他部位钢箱梁及导梁,采用线性减缩积分单元C3D8R来模拟钢垫块。钢导梁、垫块和钢箱梁的质量密度均为7.85×103kg/m3,弹性模量E为206 GPa,泊松比μ为0.3。钢梁整体网格的划分较为粗略,设置为0.2 m,支承区域及其附近的钢箱底板和垫块网格加密至0.05 m,结果已收敛[14]。全模型共划分178 762个单元,其中壳单元177 013个;杆单元549个;实体单元1 200个。
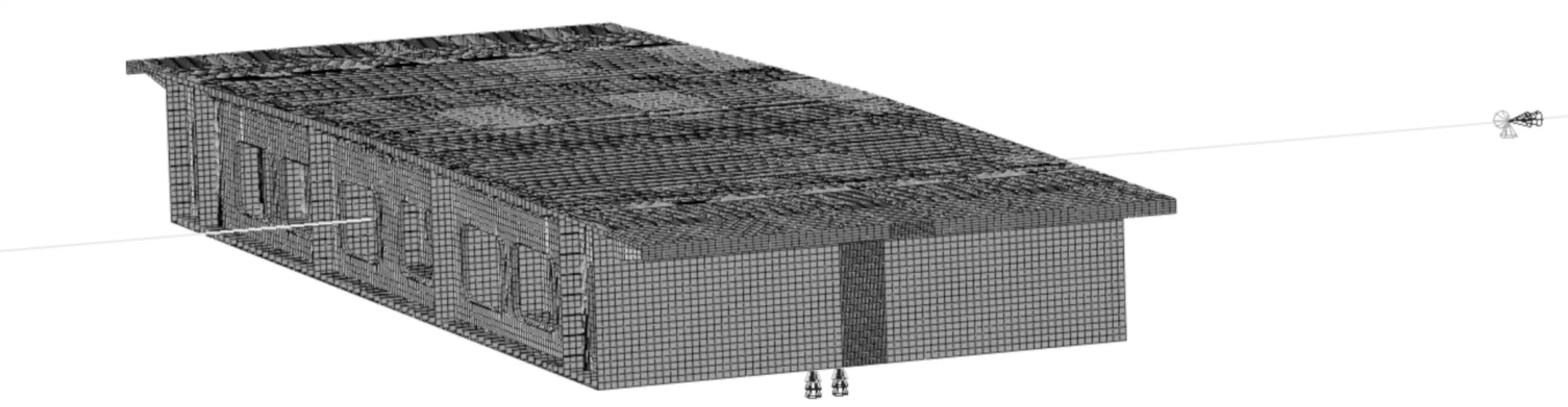
图6 梁-壳-实-接触混合有限元模型
2)边界条件的确定。因为需满足交界处截面上的壳单元和梁单元受力及变形之间的协调性,所以梁与壳结合的部分采用刚域耦合[15],耦合约束放大图如图7所示。钢垫块与钢梁之间相互作用,其边界条件采用面-面接触单元进行模拟。以刚度较小的钢梁接触面作为从表面,钢垫块接触面作为主表面。接触面之间采用切向无摩擦(模拟一次落架)、法向硬接触(模拟只受压),因对切向摩擦不做考虑,故接触对之间采用有限滑移。钢垫块底部固结,未考虑钢垫梁、步履式顶推设备及其细部构造。模型中X,Y,Z轴分别代表横桥向、竖桥向和纵桥向。在相对应的临时墩处设置一支点,通过该支点约束X,Y方向平动,不约束Z纵桥向平动。

图7 刚域耦合放大图
3)计算荷载及加载方式。导梁和钢箱梁的恒载分为结构自重和横隔板荷载两部分。结构自重通过惯性力施加,重力加速度为-10 m/s2,横隔板荷载通过均布荷载施加,大小为13 kN/m。加载时支承垫块作用在梁段中两块横隔板之间的普通截面上。支承垫块与梁底接触尺寸可以等效为0.75 m×0.5 m,该有效接触面积为0.375 m2。
2.2.2 局部应力分析
由模型计算可得钢箱梁应力云图如图8所示。钢箱梁主要受力板件及垫块的等效应力值如表3所示。由图8和表3可知:1)支承位置及其附近区域钢箱梁底板应力约为189.4 MPa,垫块应力为156.5 MPa,二者均在弹性范围内,比较安全;2)腹板在底腹板交界处小部分区域出现了应力集中的情况,这是由于底板在支反力的作用下向上凸起,而在交界处的底板凸起被腹板所限制,Mises应力最大为321.2 MPa,然而应力扩散较快,已超出设计容许应力[σ]=210 MPa。
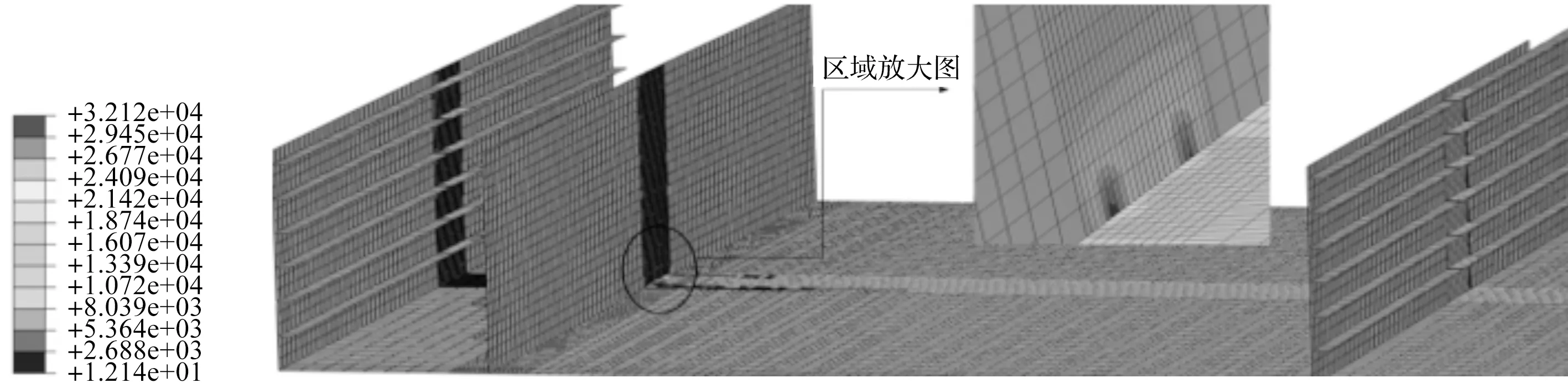
图8 钢箱梁等效应力云图
2.2.3 局部稳定分析
结构弹性稳定分析属于第一类失稳问题,钢箱梁与垫块接触区域易失稳,且发生比较突然,故对其分析尤为重要。在ABAQUS中所对应的分析类型为线性摄动中的屈曲分析,经模型分析第一阶弹性屈曲发生在支承处的底腹板交界处,屈曲系数为4.348 7,其变形云图如图9所示。图9计算结果表明钢箱梁局部稳定性满足规范要求。
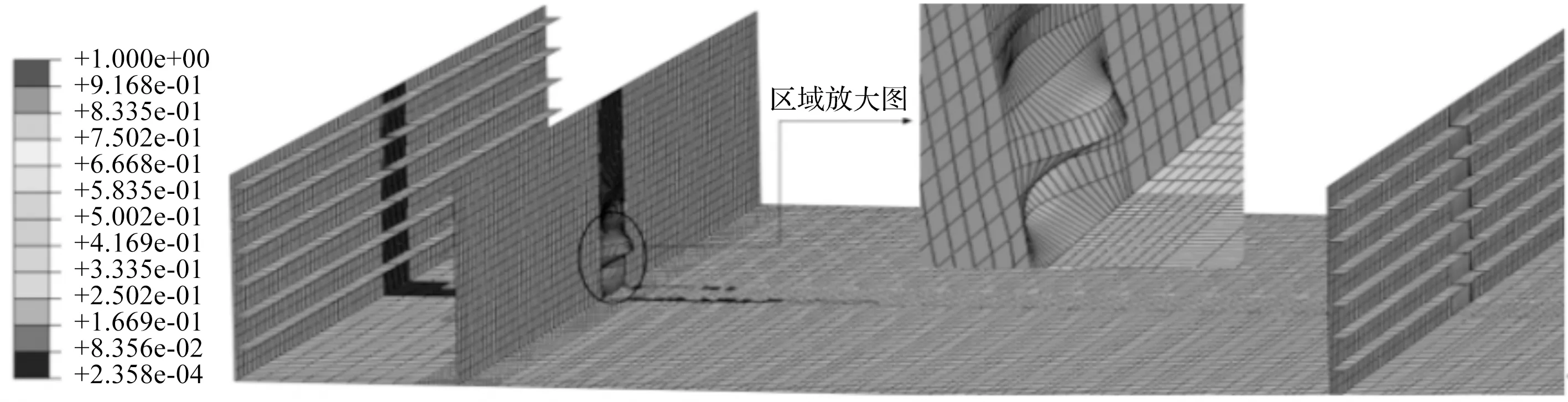
图9 第一阶屈曲变形云图(单位:cm)
2.3 结果分析
在典型不利工况下,由局部有限元模型分析可得钢箱梁各板件的大致应力情况。在顶推过程中,底板和腹板是主要的受力板件,横隔板主要是增强钢箱梁横向刚度,保持截面形状。模型中应力较大的区域主要集中在底板与腹板的连接位置,施工过程中局部应力较大是由于钢箱梁与顶推设备上垫块直接相接触,该处直接承受垫板对钢箱梁的支反力,同时因受力面积较小,接触区域容易出现应力集中、较大的现象,在施工过程中通过加固措施使该区域应力控在合理范围内即可。当支反力作用在两横隔板之间,其中底腹板受力最为不利。若不采取措施,在顶推过程中底腹板可能发生严重的、永久的变形,给顶推带来危险,因此有必要对该处及附近区域的板件进行加固。
3 改善措施研究
通过局部受力分析计算,可以得出较大应力区域的范围,可以针对该区域对钢箱进行优化,提出以下两种优方案,确保顶推施工的安全性。
方案1:对底板和腹板交界区域进行局部加强处理,采用焊接角隅加劲肋,对钢箱梁进行加固。
方案2:在底腹板交界处一定范围内对板件进行加厚处理。
3.1 方案1的钢箱梁局部受力分析
为了保证在顶推过程的安全性,可以通过优化结构构造来改善局部应力水平。在底板和腹板交界处增焊角隅加劲肋对钢箱梁进行补强,且此加劲肋可进一步提高底腹板的整体性,提高高应力区域纵横向刚度,故其抵抗变形能力得到增强。角隅加劲肋采用梯形截面,顶宽17.8 cm,底宽47.4 cm,高104.5 cm,沿钢箱纵向每隔30 cm布置,加劲肋板厚14 mm,局部补强模型如图10所示。根据建模计算,得出角隅加劲肋补强后各主要受力板件的等效应力值如表4所示,角隅加劲肋最大等效应力为105.4 MPa。各板件随补强后的最大应力变化与原方案进行更直观的比较,结果如图11所示。
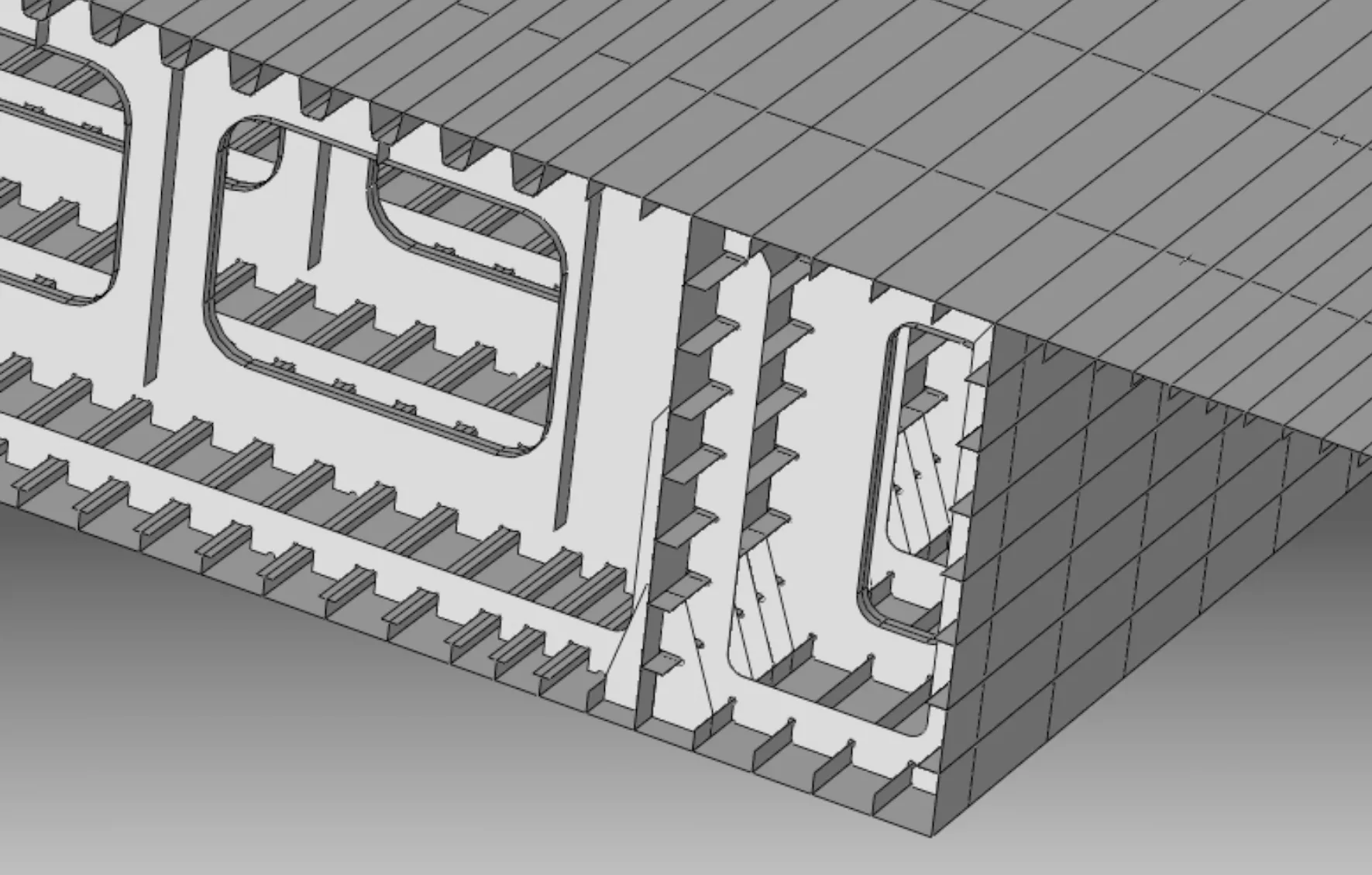
图10 钢箱焊接角隅加劲肋
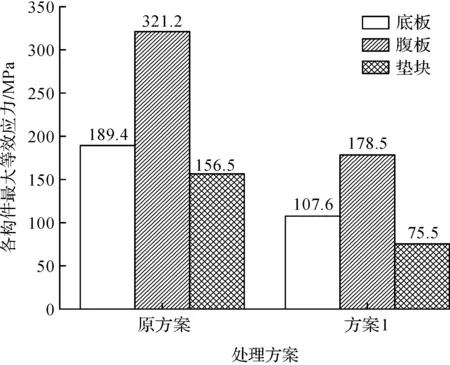
图11 原方案与方案1应力对比
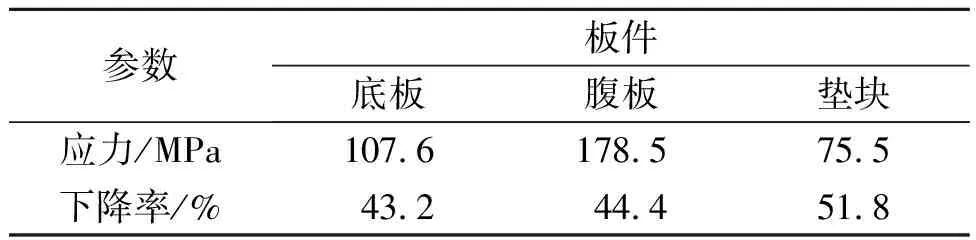
表4 方案1各板件的等效应力值
由表4和图11可知:各板件的应力低于设计容许应力值,均有明显的下降,底板应力减少了43.2%,腹板降低了44.4%,钢垫块应力值下降了51.8%。通过角隅加劲肋的补强后,钢箱的应力明显得到了改善。在顶推过程中只需控制顶推精度,钢箱不会发生屈服而对顶推造成影响,因此通过方案1在底板与腹板交界处焊接角隅加劲肋来改善钢箱应力情况是可行的。
3.2 方案2的钢箱梁局部受力分析
为了改善底板与系梁内腹板交界处附近的高应力情况,在交界处附近1 m范围内对底腹板进行加厚处理,原钢箱板件厚度如下:系梁内腹板16 mm,底板16 mm。加厚处理方案分为3种,每种方案腹板加厚4 mm,底板加厚2 mm,具体方案为
方案2-1:系梁内腹板20 mm,底板18 mm。
方案2-2:系梁内腹板24 mm,底板20 mm。
方案2-3:系梁内腹板28 mm,底板22 mm。
分别对以上3种方案进行建模计算,得出各板件的最大等效应力值如表5所示。不同局部加厚厚度下主要受力板件的最大等效应力变化趋势如图12所示。
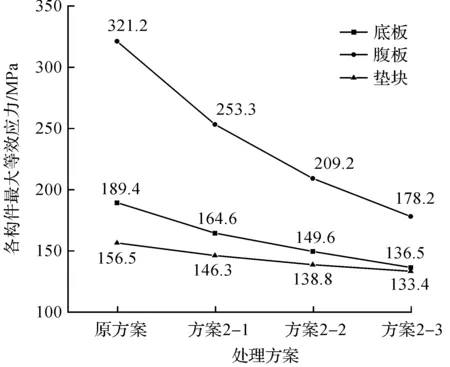
图12 原方案与方案2应力对比
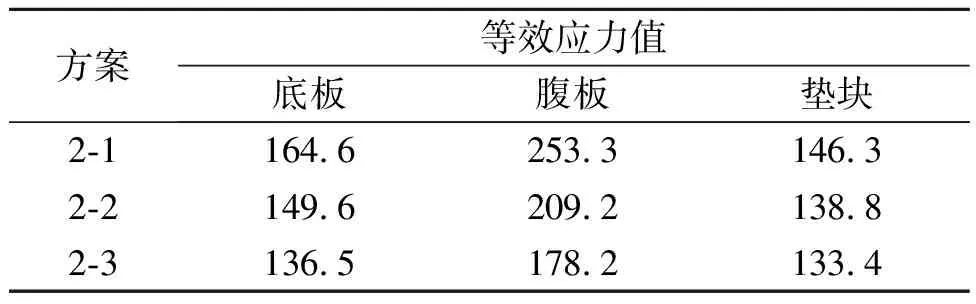
表5 方案2各板件等效应力值
由表5和图12可知:随着板件厚度的增加,钢箱各板件应力水平有所降低。与原方案相比,方案2-3中腹板应力值减小了143.0 MPa,降低了44.5%,效果比较明显。因为底腹板是直接与垫块相接触,其为关键受力板件,应力水平较大,局部増加底腹板厚度,所以能够大大改善底腹板应力情况。由此可知:原先处于较大应力状态的板件应力水平在弹性范围内,虽然局部进行加厚处理对钢箱应力改善明显,但是各板件应力值减小幅度随着板件厚度增加而下降。
3.3 方案对比分析
经建模计算,发现两种方案对钢箱梁板件的应力水平情况均有较好的改善效果,其中方案1的效果更佳;方案2通过增大板件厚度来改善钢箱应力情况。由上述规律可知:各板件的应力值虽然还会继续减小,但是下降的幅度会越来越小,且会造成较高的经济成本,在钢箱梁制造完成后进行局部加厚处理也存在较大的施工难度。相较于方案2,方案1增焊角隅加劲肋的方法提高了支承区域钢箱的整体性,使得该支承处抵抗变形能力显著上升,其应力改善效果更明显。通过以上分析,提议采取方案1对钢箱梁进行局部加固优化,实际中该桥的顶推也是采用了该优化方案来确保顶推的顺利进行,而后钢箱梁梁段通过钢混结合段与混凝土梁段连接成为主梁梁段,成桥状态时主拱钢箱梁的应力主要是由自重以及车辆荷载等活载影响而下挠造成的,主拱钢箱梁制作加工时设置了预拱度并有一定的富余量,成桥后的主拱钢箱梁应力图如图13所示,满足规范要求。
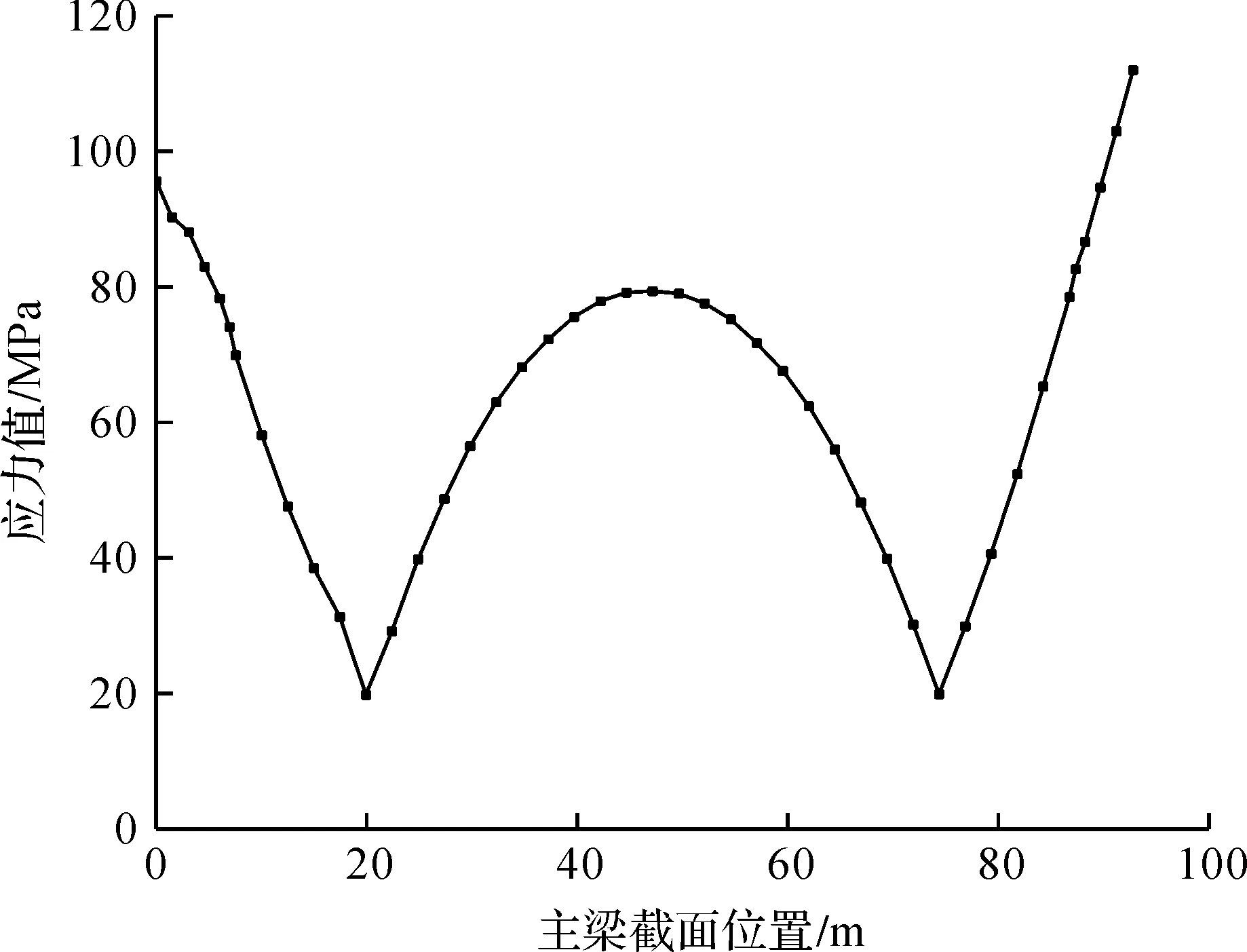
图13 成桥状态时主拱钢箱梁应力图
4 结 论
首先,通过桥梁专用软件Midas/Civil建模进行顶推施工仿真分析,确定顶推中典型不利工况为前导梁即将上9号墩,顶推至8号临时墩(此时F段钢箱梁位于8号临时墩),出现最大支反力,前导梁下挠量也达到最大;然后,采用通用有限元软件ABAQUS对典型不利工况下的钢箱进行局部应力及局部稳定分析,底腹板作为主要受力板件,其最大等效应力值相较于其他板件较为突出,分析得到在支承区域的底板与腹板交界处附近应力水平值较大,该处直接和垫块接触承受其支反力,在顶推过程中对此处应高度重视;最后,针对底板与腹板交界处附近应力较大的问题,提出了两种改善方案:方案1采用在其增焊角隅加劲肋;方案2在该交界处各沿1 m处进行板件局部加厚。经过建模计算可以看出方案一效果更佳,其不仅进一步提高了钢箱危险区域的整体性,使得该区域抵抗变形能力增强,而且施工难度较小,局部应力计算结果与局部稳定满足安全要求。通过增焊角隅加劲肋的方式能较好地应用于钢箱梁顶推施工,为同类桥型的钢梁顶推施工提供参考。
本文得到了中南林业科技大学引进人才科研启动基金项目(ZK2021YJ036)的资助。

