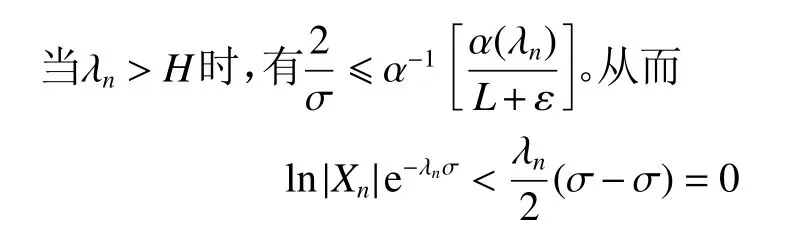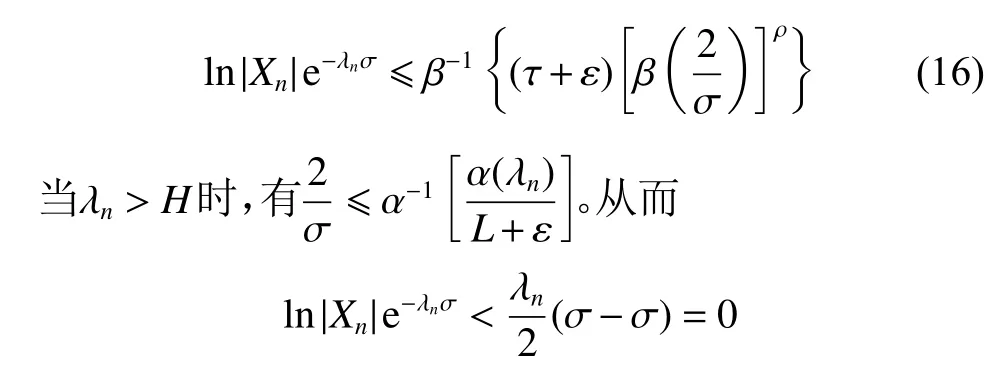随机Dirichlet级数在右半平面的广义逼近
洪甜甜,霍颖莹
(广东工业大学 数学与统计学院,广东 广州 510520)
1 基本介绍
在Dirichlet级数增长性和相关方面,众多数学工作者已经取得了一系列重要研究成果[1-4]。其中有很多关于整函数的研究,例如,Ritt定义了由Dirichlet级数所确定的增函数的级和下级,用来描述级数的增长性。随后,2010年孔荫莹和甘会林[5]通过引入一族函数,定义了更精确的广义级,并得到广义级与其系数和指数之间的关系。另一方面,徐洪焱和易才凤[6]从Dirichlet多项式估计Dirichlet级数时得到的误差着手,探讨了其与Dirichlet级数的级之间的关系。随机Dirichlet级数本质上是一族Dirichlet级数。1932年,Paley和Zygmund研究了Steinhaus-Dirichlet级数和Rademacher-Dirichlet级数两类以独立随机变量序列为系数的随机Dirichlet级数的收敛性。随后,余家荣[7]进一步讨论了以独立随机变量序列为系数的随机Dirichlet级数的收敛性问题。丁晓庆和肖益民[8]借助Dirichlet级数研究了系数为独立且一致非退化的随机Dirichlet级数的自然边界问题。2012年,孔荫莹和霍颖莹[9]在广义级的基础上,探讨了一类以独立随机变量序列为系数的随机Dirichlet级数的最大模与最大项指标之间的关系。但在现实中,独立这一条件并不具有普遍性,而且也难以检验。自然的想法是,当随机变量序列为非独立时,随机Dirichlet级数会具有什么性质?本文将在此基础上,去研究一类系数是非独立的随机变量序列 φ混合序列的随机Dirichlet级数的广义逼近。其中,φ混合序列是由Ibragimov[10]引入的,表明了变量在指标之差趋于无穷时渐进独立,关于其更多的性质可以参考文献[10-11]。
下面给出与本文相关的定义与记号,为了方便起见,本文将C表示为一个常数,并且出现先后表示不同的常数。其他记号请参看文献[1]。
定义1[1]设Dirichlet级数
式中:{bn} 是 一正实数数列,0 <λn↑∞,s=σ+it表示一复变量。
假设级数g(s)满足
那么由式(3)和文献[1]中引理3.1.1可得
式(3)、(4)中:Dh≤1。从而有
若令σc, σu, σa分 别表示级数g(s)的收敛、一致收敛和绝对收敛横坐标,则由Valiron公式
可得
即级数g(s)在右半平面是收敛、一致收敛和绝对收敛的。因此,对于任意的 σ>0,可以分别定义级数g(s)的最大模、最大项以及最大项指标为
为了描述慢增长( ρ=0)整函数的增长性,下面引入广义级和广义型。令Λ 表示满足以下两个条件的函数α (x)所构成的集合。
条件1 α(x) 是定义在( −∞, +∞)上的函数,当x≤0 时,α (x) 为常数;当x>0 时,α (x)为严格递增,取值为正的可微函数。
条件2 令d 表示微分符号,存在p∈N,使得
式中:l n[p]x=ln[p−1]lnx。
定义2[12]设α (x)∈Λ ,则级数g(s)的广义级为
若ρ ∈(0, ∞),则级数g(s)的广义型为
式中:β(lnx)=α(x) 。特别地,当α (x)=lnx时,广义级和型分别为Ritt级和Ritt型。此外,根据参考文献[12]中的引理2.3可知,对于级数g(s),当E∈(0,∞)时,有
为了证明本文所得到的结论,在这里将构造与级数相应的Newton多边形,并得到与级数式(1)具有相同广义级和广义型的Dirichlet级数。具体作法如下。
第1步 取定σ >0 ,过XOY平面上点列
中的每一点,作斜率为 −σ的直线,进而可以得到斜率为− σ的直线所构成的集合
由于每一条直线都对应一个在y轴的截距,因此可以得到级数g(s)在 σ 时的最大项满足
第2步 根据 σ的任意性,便可以得到对于任意的一个σ >0 ,级数g(s)的 最大项m(σ,g)和最大项指标n(σ)。又n(σ)为 关于σ 的增函数,从而为阶梯函数且至多只有可数个间断点,其间断点集记为 {σl},相应地,n(σl)=nl+1。最后再通过依次连接最大项指标所对应的点
便得到级数g(s)所 对应的Newton多边形Π (g)。
由Newton多边形 Π (g) 的作法,不难发现Π (g)的顶点是点列 {An} 中 的部分点,因此不妨设Π (g)的顶点为
若令
则
此外,由 σl的作法可知,对于任意的σ >0,存在σl和σl+1,使得σ ∈(σl+1,σl],有n(σ)=nl。
从而得到级数
式中:{nl}⊂{n} ,则对于任意的正数σ ,存在 σl,满足σ ∈(σl+1,σl],从而
即级数g(s)和g(s)有相同的广义级和广义型。
下文还需要给出级数误差的定义。
定义3[6]令 ϕk表示阶数不大于k的所有Dirichlet多项式所构成的集合,则对于任意给定的α(0<α<∞)和 正整数n,可以定义级数g(s)的误差为
为了证明本文提出的结论,还要给出φ 混合序列的定义。
定义4[10]{Xn}是 定义在概率空间( Ω,F, P)上的复值随机变量,P 为F上的概率,对于任意的n,m∈N,当n→∞时,若
则称{Xn}是 φ 混合序列,其中
为σ 域。
通过φ 混合序列的定义不难发现,如果对于任意的n∈N ,都满足φ (n)=0 ,那么对于任意的A∈Fm0,B∈,可以得到
即随机序列{Xn}独立。
定义5[1]设随机Dirichlet级数
式中:0<λn↑∞,s=σ+it(σ,t∈R),{Xn}是定义在概率空间( Ω,F, P)上 的φ 混 合序列,并且满足( MZ)*[13]条件,即对于任意的正整数n,存在正数d1,使得
本文假设随机Dirichlet级数fω(s)满足式(2)、(3)、(6),那么对于级数fω(s)而言,可以得到有关于它的收敛性的结论。
定理1对于任意的ω ∈Ω, a.s.,级数fω(s)在右半平面上收敛、一致收敛、绝对收敛,即
式中:σc(ω),σu(ω),σa(ω) 分别为级数fω(s)的收敛、一致收敛和绝对收敛横坐标。
此外,本文还得到误差与级之间的关系。
定理2对于任意的 ω ∈Ω, a.s.,级数fω(s)和g(s)的偏差在右半平面上的广义级一致,即
(1) 当p=1时,
(2) 当p=2, 3, ···时,
定理3若级数fω(s) 的 广义级ρ ∈(1,∞),则对于任意的ω ∈Ω, a.s.,级数fω(s)和g(s)的误差在右半平面上的广义型一致,即
推论1设级数fω(s)满足式(2)、(3)、(6),则对于任意的ω ∈Ω, a.s.,有
(1) 当p=1时,
(2) 当p=2, 3, ···时,
推论2设级数fω(s)满足式(2)、(3)、(6),并且级数fω(s) 的 广 义 级ρ ∈(1,∞) ,则 对 于 任 意 的ω ∈Ω,a.s.,有
2 一些引理
引理1[14]若 {Xn}是 φ 混合序列,并且满足式(6),则对于任意的 ω ∈Ω, a.s.,存在N(ω)>0 ,当n>N(ω)时,有
且对于{Xn}的任意子列{Xnk},有
为了证明所提出的结论,还需要用到误差与系数、最大项之间的关系。
引理2[6]若级数g(s)满足式(2)、(3),那么对于任意的n∈N ,任意的α (0<α<∞)以及充分小的正数,有
式中:T是与σ ,n无关的常数。
其次,广义级函数有以下性质。
引理3[12]设α (x)∈Λ,则
(1) 对于任意的正数C1,C2以 及实数A:
(2) 对于任意的0 (3) 当p=1时 ,对任意A>0,存在使得 证明 对于该引理(1)、(2)的证明,可以参考文献[12]中的引理2.2。下证明(3)、(4)。 首先,由α (x)的性质 可知,对任意正数δ,存在X(δ)>0,当x>X(δ)时, 下文先证明引理3(3)。 下文再证明引理3(4)。 又由引理3(2) 可得 证毕。 引理4 对于级数fω(s) ,当E∈(0,∞)时,对于任意的ω ∈Ω, a.s., 证明 与参考文献[12]中的引理2.3类似,此处不再证明。 引理5[15]级数g(s)满足式(2)、(3) ,则 (1) 当p=1时: (2) 当p=2, 3, ···时: 最后,还需要用到以下结论。 引理6[7]设b, σ ∈(0,+∞),则函数 定理1证明 首先由式(4) ,即 和式(7)可知,对于任意的 ε>0 和任意的ω ∈Ω, a.s.,存在N1∈N ,当n>N1时, 其次由式(8)可知,序列{Xn}存 在一子列{Xnk}满足 因此,有 最后由Valiron公式可得 证毕。 定理2证明 首先,根据引理4可知,对于任意的ω ∈Ω, a.s.,M(σ,fω) 可 以用m(σ,fω)替换。 下记An,α(g,α)=En−1(g,α)eλnα。并令 则对任意的正数ε ,存在N(ε)>0 ,使得当n>N(ε)时,有 再由引理2可得 最后由式(7)和式(4)可得,对于任意的 ε >0,存在N(ε)>0,使得当n>N(ε)时 ,对任意的ω ∈Ω, a.s.,有 情形(1) 当p=1时 ,首先由α (x)的单调性,引理 其次,由α (x)的性质 可知,对于任意的正数 δ ,存在N(δ)>0,使得当n>N(δ)时,有 最 后,当 σ>0 充 分 小时,有n(σ)>N(ε),由α(x) 的单调性以及引理3(1) 可得,对于任意的ω ∈Ω,a.s.,有 且 因此,当σ >0充分小时, 当σ >0充分小时,令 则对任意n>N(ε),当λn≤H时,有 所以对于任意的n>N(ε),式(12)成立,因此对于任意的ω ∈Ω,a.s.,有 下证等式成立。 情形(1) 由Newton多边形作法和引理5(1)可知,存在级数式(5),满足 并记n(σl)=nl。记 此外,由式(8)可知,存在 Ω0满足P (Ω0)=0,使得对任意的ω ∈(Ω−Ω0),有 并且由 P(Fε0)>0 得,( Ω−Ω0)∩Fm0≠ϕ。从 而 存在ω0∈(Ω−Ω0)∩Fm0,对序列{Xnl(ω0)}存在的子列,不妨仍记为{Xnl(ω0)},满足 从而 即 因此 与式(13)式矛盾。证毕。 情形(2) 同情形1证明类似,此处不再证明。 定理3证明 首先由引理4可知,对于任意的ω ∈Ω,a.s.,M(σ,fω) 可以用m(σ,fω)替换。 下记An,α(g,α)=En−1(g,α)eλnα。并令 则对于任意的正数ε ,存在N(ε)>0 ,使得当n>N(ε)时,有 又由引理2可得 最后由式(4),即 和式(17)可得,对于任意的ε >0 ,存在N(ε)>0,使得当n>N(ε) 时 ,对任意的ω ∈Ω, a.s.,有 由于 β(lnx)=α(x),因此由引理3(4) 以及式(15)可得,存在 0 且 因此,当σ >0充分小时, 当σ >0充分小时,令 则对任意n>N(ε),当λn≤H时,有 所以对任意n>N(ε),式(16)成立,因此对于任意的ω ∈Ω, a.s.,有 下证等式成立。由Newton多边形作法和引理5(3)可知,存在级数式(5),满足 再选取序列{ σ}的 子列{ σl},使得 并记n(σl)=nl,记 若 P(F>0 ,则存在ε0>0 ,使得P (Fε0)>0成立,即对于任意的ω ∈Fε0,有 此外,由式(8)可知,存在 Ω0满足P (Ω0)=0,使得对任意的ω ∈(Ω−Ω0),有 且 由 P(Fε0)>0 得,( Ω−Ω0)∩Fm0≠ϕ。从 而 存 在ω0∈(Ω−Ω0)∩Fm0,对序列{Xnl(ω0)}存在的子列,不妨仍记为{Xnl(ω0)},满足 从而 即 因此 与式(17)矛盾。证毕。
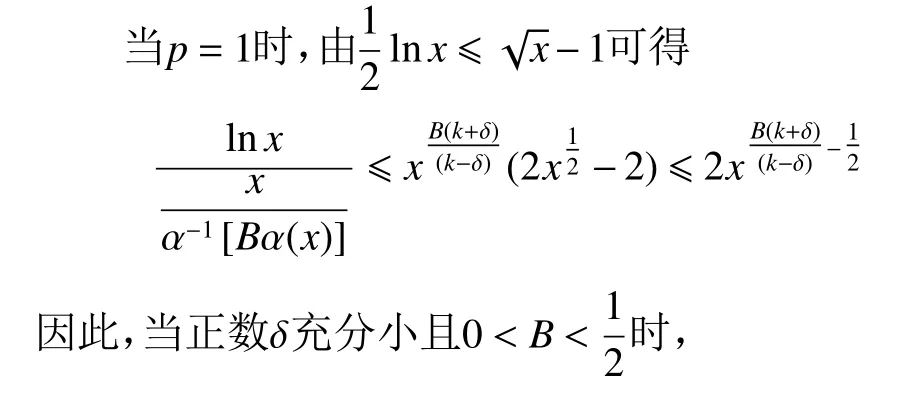
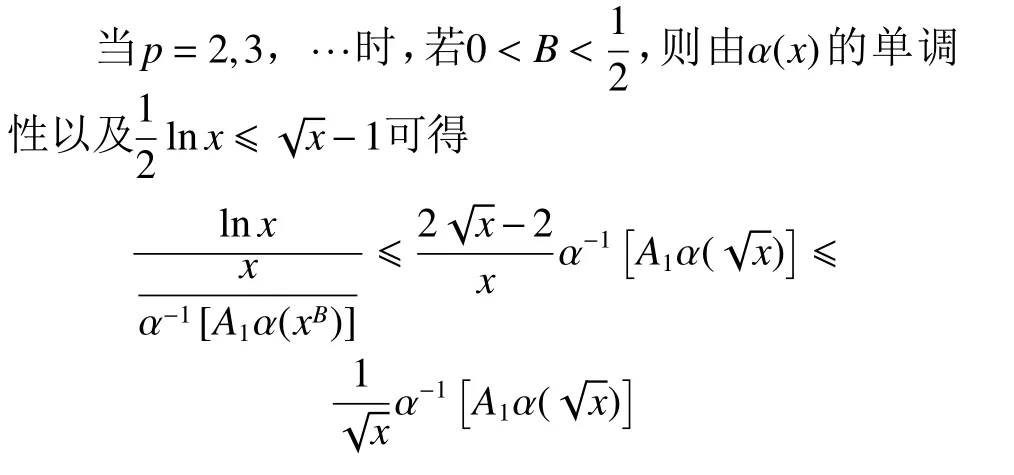
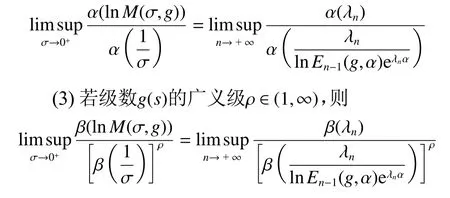
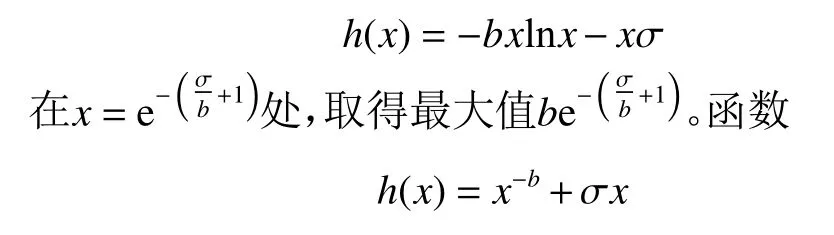

3 定理证明