多级压裂一界面破坏试验及数值模拟研究*

汪衍刚 冯永存 邓金根 闫伟 李晓蓉 赵英晓

(中国石油大学(北京) 油气资源与探测国家重点实验室)

0 引 言

多级水力压裂是页岩油气开发必不可少的技术手段, 在多段水力压裂过程中井筒内会经历多轮次压力升降波动, 套管-水泥环-地层系统应力会随之产生变化, 井筒系统内应力水平一旦超过其所能承受的极限, 井筒完整性便会产生破坏, 严重威胁油气井后续施工作业[1-9]。 井筒完整性破坏有套管本体破坏、 水泥环本体破坏、 套管-水泥环界面(一界面) 和水泥环-地层界面(二界面) 破坏4种形式。 相较套管和水泥环本体而言, 两界面更为薄弱易损, 因套管与水泥环弹性力学性质差异程度高于水泥环与地层弹性力学性质差异程度, 使得一界面相较二界面更易产生破坏, 这一点也被国内外众多研究学者所证实[10-12], 因此一界面破坏问题一直是页岩油气井压裂中的研究重点。 针对一界面破坏研究, 部分学者采用试验直接测试[13-19], 通过建立大型套管水泥环物理模型装置研究井筒完整性破坏规律, 但大型物模系统复杂度及成本较高且效率低下, 严重制约一界面破坏高效性、 系统性研究。 也有学者采用数值模拟方法研究一界面破坏问题[20-27], 其基本手段一般基于ABAQUS 有限元软件建立套管-水泥环-地层有限元模型, 在一界面布置一层Cohesive (内聚力) 单元, 以Cohesive 单元的损伤和破坏来等效模拟界面的损伤与破坏。Cohesive 单元参数与一界面真实物理胶结参数的相符程度决定着数值模拟精度的高低, 但目前一界面Cohesive 单元参数往往凭经验设定, 与真实物理情况相符程度未知, 因此Cohesive 单元法能否准确反映一界面实际破坏过程有较大不确定性。

鉴于目前2 种研究方式的局限性, 笔者拟结合试验与数值模拟方法研究一界面破坏问题, 制作一界面胶结参数测试装置, 通过试验获取界面胶结参数, 建立套管-水泥环-地层有限元模型, 在套管-水泥环界面布置Cohesive 单元, 将实测界面胶结参数赋予Cohesive 单元, 实现对压裂过程中套管内压波动导致一界面破坏的模拟研究。

1 Cohesive 单元模型

Cohesive 单元采用牵引力分离准则, 主要包括单元起始损伤和损伤演化2 个阶段。 固井双界面失效模拟一般采用最大主应力及临界断裂能方式作为Cohesive 单元的起始损伤及完全失效判据。 单元参数主要包括: 法向强度、 法向刚度、 法向断裂能、切向强度、 切向刚度及切向断裂能。 图1 为一个典型的双线性牵引分离本构模型示意图。

图1 Cohesive 单元双线性本构模型Fig.1 Bilinear constitutive model of cohesive elements

图1 中,K、G、T分别为刚度、 断裂能和牵引力, 下标n、 s、 t 分别代表法向、 切向1、 切向2。 从图1 可知, 当单元应力状态处于AB区间时,单元处于弹性阶段, 其刚度为K; 当应力水平达到极限强度T后单元刚度开始退化损伤; 当单元损伤持续进行过程中所消耗的能量达到断裂能G临界值后, 单元完全失效破坏。

2 一界面胶结参数测试

2.1 试验装置及试件养护

套管-水泥环试件养护如图2 所示。

图2 套管-水泥环试件养护Fig.2 Curing of casing-cement specimens

为测试一界面切向和法向胶结参数, 分别制作了切向和法向胶结参数测试装置。 从N80 套管上取出圆柱形试样作为模拟套管, 取出矩形试样作为套管片, 试样(见图2a) 表面经打磨后与实际套管表面粗糙度一致。 模拟套管和套管片, 分别用于测试切向胶结参数和法向胶结参数。 将取自固井现场的水泥浆均匀注入测试工具槽内, 模拟套管和套管片分别放置到切向胶结参数测试和法向胶结参数测试工具槽内, 使水泥和试样胶结在一起并置于养护箱内养护, 如图2b 所示。 养护条件为: 常压,温度50 ℃, 时间48 h。

2.2 切向及法向胶结参数测试

将养护好的切向胶结参数测试装置和法向胶结参数测试装置放到力学测试机下, 分别对模拟套管及套管片顶部向下施加压力, 控制压头速度为5 mm/min, 记录测试过程中的切向载荷-位移数据和法向载荷-位移数据, 直至试件胶结破坏。 测试过程如图3 所示。

图3 套管-水泥环界面切向及法向脱黏测试Fig.3 Tangential and normal debonding tests of the casing-cement interface

将界面切向胶结参数测试过程中所得载荷数据转换为应力数据, 得到界面切向应力-位移关系。载荷与应力转换公式如下:

式中:Ss为界面切向应力, MPa;P为载荷, N;h为圆柱形模拟套管高度, mm;r为圆柱形模拟套管直径, mm。

切向测试结果如图4 所示。 测试数据中的切向应力最大值(B点纵坐标值) 为界面切向胶接强度ts, 其值为1.81 MPa。 对最高点之前的数据采用最小二乘法进行线性拟合, 得到上升段AB拟合直线方程, 斜率为界面切向胶结刚度Ks(89.9 MPa/mm)。 对最高点之后的数据采用最小二乘法进行线性拟合, 得到下降段BC拟合直线方程。 上升段拟合直线AB、 下降段拟合直线BC与X轴所围成的面积为切向胶结断裂能gs(0.12 mJ/mm2)。

图4 套管-水泥环切向脱黏测试拟合结果Fig.4 Test and fitting results of the casing-cement interface tangential debonding

将法向胶结参数测试过程中所得载荷数据转换为应力数据, 形成界面法向应力-位移关系。 载荷与应力转换如下:

式中:Sn为界面法向应力, MPa;w为矩形套管片宽度, mm;l为矩形套管片与水泥胶结长度之间的宽度, mm。

法向测试结果如图5 所示。

图5 套管-水泥环法向脱黏测试拟合结果Fig.5 Test and fitting results of the casing-cement interface normal debonding

测试数据中的法向应力最大值(B点纵坐标值) 为界面法向胶接强度Tn, 其值为0.95 MPa。对最高点之前的数据采用最小二乘法进行线性拟合, 得到上升段AB拟合直线方程, 斜率为界面法向胶结刚度Kn(37.2 MPa/mm)。 对最高点之后的数据采用最小二乘法进行线性拟合, 得到下降段BC拟合直线方程。

上升段拟合直线AB、 下降段拟合直线BC与X轴所围成的面积即为法向胶结断裂能gn(0.06 mJ/mm2)。

3 数值模拟

3.1 有限元模型建立

基于某页岩气开发水平井地质情况及井身结构, 利用ABAQUS 软件建立水平段套管-水泥环-地层组合体三维有限元模型, 如图6 所示。 设置模型尺寸为3 m×3 m×10 m, 套管外径127 mm, 水泥环外径158 mm, 在一界面插入一层Cohesive 单元,套管、 水泥环与地层均采用三维实体单元; 在靠近井筒位置进行网格加密, 沿井眼至地层远端网格密度逐步降低。

图6 套管-水泥环-地层有限元模型Fig.6 Casing-cement-formation finite element model

3.2 有限元模型参数

数值模拟研究对象为某页岩气井垂深3 300 m处水平段, 地层最大水平主应力、 最小水平主应力、 垂直应力分别为58、 40 及47 MPa, 套管材料采用弹性模型, 水泥环及地层材料采用Mohr-Coulomb 模型, 具体材料参数如表1 所示。 Cohesive 单元参数为试验所测实际值(见表2), Cohesive 单元破坏采用能量损伤演化BK 准则。

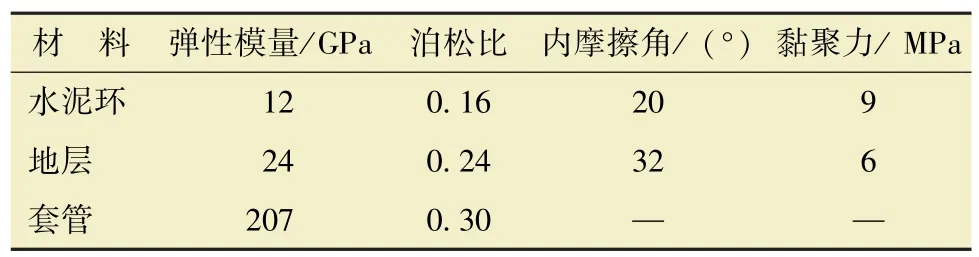
表1 套管、 水泥环和地层材料属性Table 1 Material properties of casing,cement sheath and formations

表2 Cohesive 单元材料属性Table 2 Material properties of cohesive elements

基于压裂现场施工参数设置套管交变内压以对真实压裂过程进行复现, 每轮次分为增压和泄压2个阶段, 增压、 泄压交替进行。 增压阶段套管内注液压力分别设为85、 95 及105 MPa, 以分析不同套管内压对一界面破坏的影响, 停泵泄压阶段套管内压均设为静液柱压力, 循环增泄压总共11 轮次,数值模型中共设置22 个时间分析步。

4 模拟结果分析

4.1 累积塑性应变及微环隙宽度关系

当套管内压分别为85、 95 及105 MPa 时, 水泥环最大等效塑性应变值及最大微环隙宽度值如图7 所示。

图7 不同内压下水泥环等效塑性应变与微环隙宽度关系曲线Fig.7 Correlations between the equivalent plastic strain of the cement sheath and the microannulus under different internal pressures

最大等效塑性应变值(PEEQ) 为水泥环中产生塑性变形最严重区域的等效塑性应变值, 最大微环隙宽度为一界面周向上最大微环隙宽度值。 将有限元模型计算结果从直角坐标系切换到柱坐标系模式下显示, 经后处理得到套管-水泥环界面微环隙宽度。

由图7 可见: 在各套管内压下首轮次压裂水泥环即产生塑性变形并形成微环隙, 一界面Cohesive单元完全损伤失效; 压裂首轮次水泥环最大等效塑性应变值分别为2.8×10-3、 5.01×10-3及6.05×10-3, 最大微环隙宽度分别为56.1、 67.3 及78.5 μm, 在压裂首轮次水泥环最大等效塑性应变及微环隙宽度增加幅度最大; 随着压裂轮次的递增, 在各内压下水泥环最大等效塑性应变及最大微环隙宽度均逐步增加, 但后续轮次增加幅度随着轮次的递增逐步减小; 11 轮次后水泥环最大等效塑性应变分别为5.54×10-3、 10.29×10-3、 12.34×10-3, 最大微环隙宽度分别为117.5、 141.6 及164.31μm。分析认为, 在增压阶段内压越高水泥环塑性变形越严重, 在泄压阶段所产生的残余变形就越大, 越难恢复原来形状, 形成的微环隙就越宽; 随着压裂轮次的递增, 水泥环塑性变形有累积效应[28], 造成后续轮次水泥环塑性变形程度及水泥环最大微环隙宽度逐步增加。 因此, 在设计压裂参数时应考虑套管内压及压裂轮次对界面微环隙形成的影响, 选取最优压裂压力及压裂轮次等参数。

4.2 水泥环塑性变形及微环隙形态

在各压力下经11 轮次循环压裂后水泥环等效塑性应变如图8 所示。 从图8 可见, 水泥环塑性变形并非均匀分布, 在径向上水泥环塑性变形程度由内壁至外壁逐渐变大, 在周向上水泥环最大塑性变形产生在最大水平主应力处。

图8 11 轮次压裂后水泥环等效塑性应变Fig.8 Equivalent plastic strains of the cement sheath after 11 times of fracturing

在各压力下经1、 3、 5、 7、 9 及11 轮次压裂后, 一界面微环隙数据如图9 所示。 从图9 可见,水泥环微环隙宽度在周向上并不一致。 由于地层三向主应力并不相等, 在套管内压和地应力共同作用下, 微环隙宽度在不同位置出现差异, 其中最大微环隙宽度产生在最大水平主应力处; 与图8 进行比较可见, 水泥环内壁塑性变形程度越大的区域界面微环隙宽度越宽。

图9 11 次压裂后微环隙宽度及形态Fig.9 Width and shape of the micro-annulus after 11 times of fracturing

由以上分析可知, 在设计压裂参数时必须考虑三向地应力的影响。

5 结论

(1) 研制了一界面切向与法向胶结参数测试装置, 基于此装置试验获得了一界面切向及法向胶结参数, 建立了套管-水泥环-地层有限元模型。将试验所得界面胶结参数赋予一界面Cohesive 单元, 使一界面破坏数值模拟最大程度贴近实际界面破坏物理情形。

(2) 在增压阶段, 套管内压越高, 水泥环塑性变形程度越大, 泄压后水泥环内壁越难恢复原来形状, 进而所产生的套管-水泥环微环隙宽度就越宽。

(3) 在多级压裂过程中, 随着压裂轮次的递增, 水泥环塑性变形程度及一界面微环隙宽度逐渐累积增加, 第一轮次水泥环等效塑性变形及微环隙宽度增加幅度最大, 后续轮次增加幅度随轮次的递增逐渐降低。

(4) 由于地层三向主应力并不均等, 水泥环塑性变形程度及一界面微环隙宽度在周向上均不一致, 在水泥环塑性变形程度越大的区域套管-水泥环界面微环隙宽度越宽。