起伏管气液两相携液能力的试验研究*
徐龙宇 张慢来, 夏齐 汪国威 廖锐全
(1. 长江大学机械工程学院 2. 中国石油天然气集团有限公司采油采气重点实验室长江大学分室)
0 引 言
随着我国石油天然气工业的发展, 气田集输管线分布越来越广, 其中, 湿气输送工艺以其流程简单高效的特点, 现阶段已成为气田集输管线的主要形式。 对于地势起伏变化的地面管线, 湿气极易形成积液, 当气量较小时, 积液增加, 明显减小气体的过流面积, 导致管线压降增大, 甚至影响管线的正常输送[1-4]。 因此, 开展起伏管气液两相携液能力研究具有重要意义。
D.H.BEGGS 等[5]通过理论推导得到考虑倾角的持液率计算关系式; H.MUKHERJEE 等[6]针对Beggs-Brill 半经验式中的问题开展试验研究并得到全部倾角范围内的相关式; XIAO J.J.等[7]针对不同的流型建立动量、 质量方程, 得到对应的持液率计算式。 国内外学者建立了倾斜管和起伏管气液两相的机理模型[8]。 A.S.KAYA 等[9]采用 Ansari 等的方法建立了微倾管的机理模型; A.R.HASAN等[10]基于漂移模型提出简易的两相流机理模型。王琦[11]开展水平气液两相流的模拟试验, 按垂直段、 水平段、 倾斜段等不同管段研究携液参数, 得出倾斜段具有相对而言最差的携液能力; SHI J.T.等[12]对倾斜管线的气液两相的携液机理进行研究,观测了不同倾斜角下的气液形成的液滴的直径及形状变化。 对于起伏管的数学动力模型也相对较少,对起伏管的动力模型做出了相关的调研。S.L.SCOTT 等[13]建立起伏管段塞流模型, 研究发现在起伏管段内, 液塞长度会发生较大变化;Y.TAITEL 等[14]建立了可以跟踪起伏管每个液塞的水动力学模型; 而SHARMA[15]则基于上述模型,建立了起伏管的段塞流跟踪模型, 这个模型能够准确预测管线中的进口压力。
Y.TAITEL 等[16]通过研究大倾角下的地形起伏管线得出: 当起伏管倾角较大时, 可以忽略由气液两相摩擦引起的压降损失, 认为压降只受液弹重力的影响; 同时在此研究基础上建立了针对两相流起伏管线流动特性预测的数学模型和方程。 周良胜[17]利用 PIPEPHASE 软件和新建立的持液率计算模型对几种简单地形起伏管段内持液率的变化情况进行模拟研究, 结果表明, 对于起伏较大的管线, 最低点与最高点间的高程差对平均持液率的影响最为明显, 而管线倾角对其影响并不显著。 梁法春[18]详细分析了地形起伏湿天然气集输管线运行时的积液动态累积过程, 以及达平衡状态时的临界积液量, 对积液累计动态过程进行预测; 模拟结果表明, 对于高气液比的某一固定管线, 设定其他条件不变时, 气相流速对管内临界积液量的影响显著, 气相携液能力随着气体流速的增大而增强, 管内临界积液量减小。
随着流体力学的发展与研究的逐渐深入, 以及瞬态流理论的逐渐成熟, 国外许多石油公司开始开发能够应用于井筒或管线的气液两相的数值模拟软件。 现阶段, 多相流数值模拟软件分为: 稳态多相流和瞬态多相流数值模拟软件, 且瞬态流的数值模拟远比稳态流要复杂。 OLGA 为常见的一种瞬态多相流数值模拟软件, 采用隐式算法来对压力、 携液量等参数进行运算求解, 更适合对起伏管线的气液两相流的模拟。 综上所述, 现阶段学者对起伏管路气液流动规律的研究大多是停留在室内模拟试验和流型判别与计算方法上, 而对倾斜管的流动规律方面的数值模拟较少。 笔者先运用室内模拟上倾管和下倾管的流动规律, 再运用仿真软件对室内管线进行数值模拟并验证数值模拟测试结果的准确性, 最后通过仿真软件对起伏管线进行模拟研究, 对起伏管进行分段研究, 判断上倾、 下倾和水平管积液的难易程度, 并将此方法用于集输管线的测试中, 为集输管线的安全运行提供理论基础。
1 倾斜管室内试验
倾斜管试验在长江大学多相流试验平台进行,试验装置如图1 所示。

图1 倾斜管流动试验装置Fig.1 Experimental device of flow in undulating pipeline
本试验选用自来水作为液相, 空气作为气相,用离心泵模拟地层产液, 水由离心泵增压后经过气相流量计、 气液混合器进入试验倾斜管; 空气压缩机模拟地层产气, 空气由空气压缩机加压后经过气相流量计、 气液混合器进入试验倾斜管; 气液经气液混合器流入试验倾斜管, 最终由倾斜管的末端气液分离, 空气排向大气, 液体排入储水罐。
设置液体流量0 ~1 m3/h, 气体流量20 ~80 m3/h; 整条管路采用透明有机玻璃管, 管线长度为13 m, 压力测试段长度为7 m。 管线中段有高速摄像机, 检测不同工况下管路流型变化; 并在管路3.8 和10.5 m 处设有压力检测设备, 通过电脑采集每秒的压力数据; 管路末端设有计量秤, 检测管路出液量。
1.1 试验数据分析
由于试验设备测量持液率不太方便, 所以此次试验中测量携液量来作为气流携液能力参数(持液率=进液量-携液量)。 试验通过记录1 min 管线末端出液量来作为携液量值, 得到上倾管的携液量随气量变化, 如图2 所示。 同理, 测量1 min 内管路3.8~10.5 m 处压降变化值来衡量气流携液过程中能量变化, 如图3 所示。

图2 不同倾角的上倾斜管的携液量Fig.2 Carrying capacity of the up-dip pipe with varied dip angles
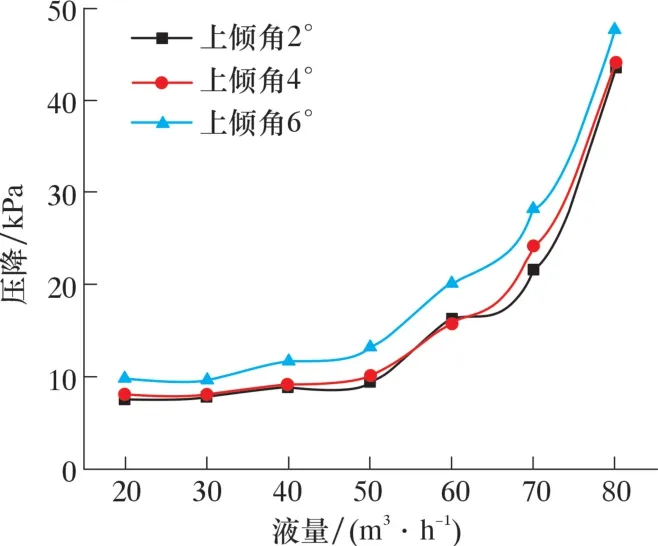
图3 不同倾角的上倾斜管的压降Fig.3 Pressure drop of the up-dip pipe with varied dip angles
由图2 可以发现, 随着气量增大, 上倾管线携液量逐渐增大, 且当气量在35 ~70 m3/h 时携液量波动较明显。 这是因为此气液比下, 管路中为段塞流, 段塞流为一种不稳定流动, 所以会呈现携液量波动趋势。 气量35~70 m3/h 下的段塞随时间推移移动的过程如图4 所示。
由图3 可以发现, 随着气量增大, 压降逐渐增大。 这是由于在上倾管中气液滑脱和气体与管壁之间的滑脱损失较大, 大于重位压力损失。 而前面整个起伏管线中压降随气量增大逐渐减小, 因此造成压力损失最大位置为凹陷管和凸起管处。
1.2 数值模拟可行性分析
运用仿真软件模拟室内试验的倾斜管, 本文选用黑油模型模拟气液两相流。 入口设置类型为Mass, 在此节点设置温度和流量, 入口温度设置为32 ℃, 入口气量为20 ~80 m3/h, 入口液量为0.1~0.3 m3/h; 出口设置类型Pressure, 在节点设置出口压力参数及流体数据, 出口压力设置为1 MPa。 管线的参数设置: 管径60 mm, 管线长度13 m, 表面粗糙度5 × 10-5m, 传热系数6.5 W/(m2·℃) , 模拟时间设置3 min。
图5 所示为液量0.1 m3/h、 气量20 ~80 m3/h下的olga 模拟携液量与试验值。 由图5 可以看出,两者非常接近, 携液量随着气量的增大近似线性增加, 表明模拟携液量的方法可行。
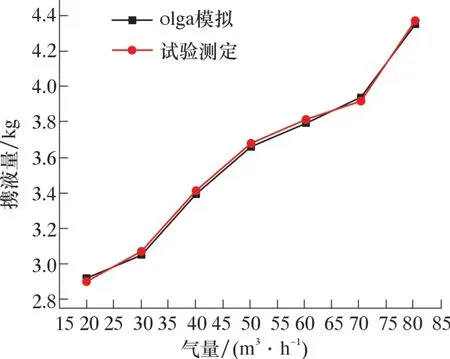
图5 试验测定与仿真模拟的数据对比Fig.5 Measured and simulated carrying capacity vs. gas flow rate
模拟的不同距离(3.8 和10.5 m) 处的压差与试验数据对比如表1 和图6 所示。

表1 压降数据对比Table 1 Comparison of pressure drops
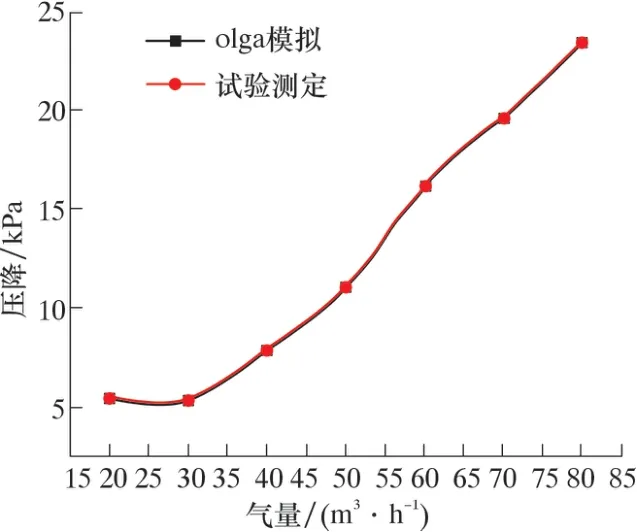
图6 仿真数据与试验模拟数据对比Fig.6 Measured and simulated pressure drop vs. gas flow rate
由图6 和表1 可见, 压降模拟值与实际数据接近, 误差小于1%。 随着气量的增加, 压降呈现快速增大趋势。 当气量为50 m3/h 时, 模拟值略小于试验值, 当气量大于50 m3/h 时, 模拟值偏大。
2 起伏管线的模拟研究
为研究起伏管线压降和积液规律, 利用数值模拟软件建立了数学模拟和几何模型, 分析气液量和倾角对起伏管线的压降和携液量变化规律的影响。
2.1 数学模型选择
对于气液两相管线而言, 为了分析气液两相的流动规律, 需要在研究过程中采用一维流动模型。目前气液两相流的瞬态模拟常用模型有3 种: 双流体、 无压波及漂流模型。 本文选用双流体模型, 因为上述3 种模型只有双流体模型针对气液两相各自单独建立了连续性方程和动量方程, 可以对气液两相进行更为深入的研究, 精度也优于另外2 种模型。
气、 液相连续模型:
气液相动量守恒方程:
式中:φ为截面含气体积分数, 无因次量;A为管线截面积, m2;HL为常数;p为压力, Pa;g为重力加速度, m/s2;ρg为气相密度, kg/m3;vg、vL分别为气相液相表现流速, m/s;θ为管线倾角,(°)。 ΔmgL为管线气相转化液相的质量流量,kg/(m·s) ; ΔmgL为管线液相转化气相的质量流量, kg /(m·s) ;Γgw、ΓLw为气、 液各相与壁面间的剪切力, N/m;Γgi、ΓLi为分别为作用在气相、 液相截面的剪切应力, N/m;v0为相变流速,m/s, 当mgL>0 时v0=vL, 当mgL<0 时v0=vg。
2.2 几何模型的建立
基于现场常出现的起伏管线轨迹, 建立了如图7 所示的简化数学模型。 该模型由100 m 下倾段、底部凹陷段、 100 m 上倾段和顶部凸起段组成。 下倾段模拟实际起伏管线的下坡流动, 上倾段模拟起伏管线的上坡流动。
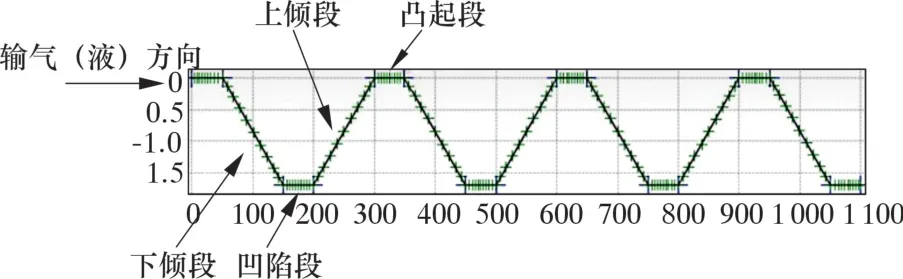
图7 起伏管线模型Fig.7 Undulating pipeline model
入口设置类型为Mass, 为流量入口, 在此节点设置温度和流量, 入口温度设置为32 ℃, 入口气量为10~200 m3/h, 入口液量为0.1 ~2.0 m3/h;出口设置类型Pressure, 为压力出口, 在节点设置出口压力参数及流体数据, 出口压设置为10 MPa。管线的参数设置: 管径60 mm、 管线长度13 m、粗糙度5×10-5m 、 传热系数6.5 W/(m2·℃) 、 模拟时间设置为60 min。
3 模拟结果分析
3.1 持液率分析
持液率反映管线截面含液体积分数, 能反映起伏管线各个位置液相占比; 携液量反映当前工况下的气体携带液体的能力; 压降则反映集输管线中气体运移液相的能量变化。 当前工况为液量0.6 m3/h、气量150 m3/h、 倾斜角6°, 得到起伏管线沿线持液率分布如图8 所示。
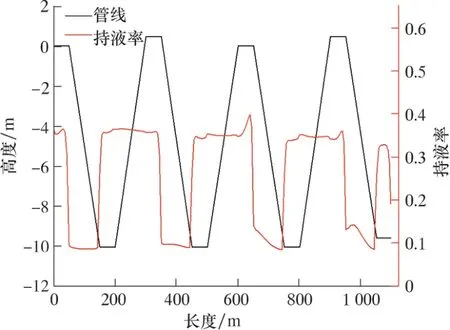
图8 管线沿线的持液率分布Fig.8 Liquid holdup distribution along the pipeline
由图8 可以发现, 随着管线运移, 下倾段持液率逐渐减小, 上倾段持液率逐渐增加。 这说明下倾段依靠自身重力作用液体较容易被带出, 上倾段由于液相要克服自身重力作用和摩阻阻力较难被带出。
底部凹陷处到下倾段指端为持液率最大位置,此处为最容易积液位置, 且随着起伏波的增多, 持液率波动性会在增大。 这是因为积液聚集在底部凹陷处到下倾段指端, 气体通过这里时会形成活塞式气顶水效果, 呈现为持液率波动性增大效果。
针对这一现象, 将对上倾段、 凹陷段和凸起段进行单独分析, 得到持液率和压降的规律, 如图9~图11 所示。
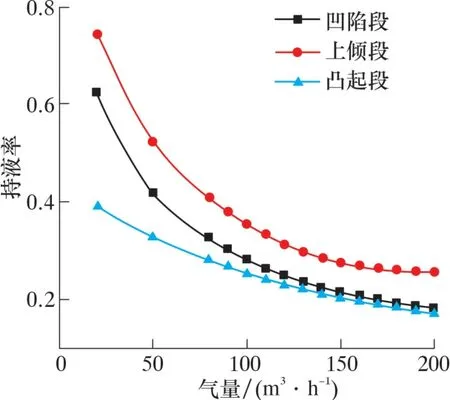
图9 管线持液率随气量变化Fig.9 Liquid holdup vs. gas flow rate
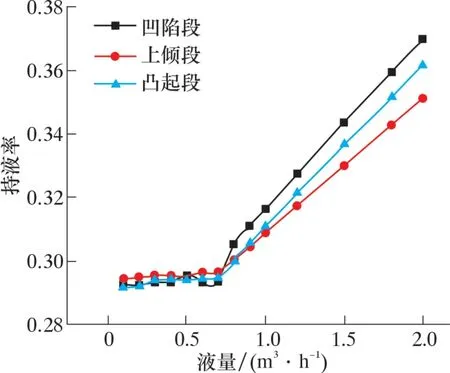
图10 管线持液率随液量变化图Fig.10 Liquid holdup vs. liquid flow rate
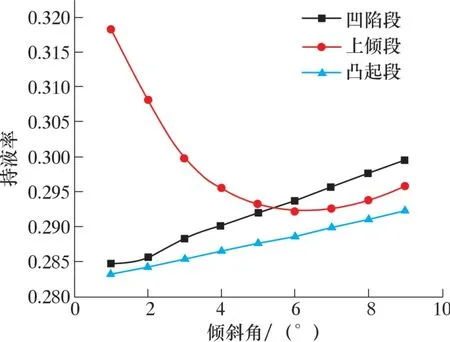
图11 管线的持液率随倾斜角变化图Fig.11 Liquid holdup vs. dip angle
由图9 可以发现: 随着气量增加, 3 种管段持液率均减小; 当气量大于150 m3/h 时, 携液难易程度为上倾段>凹陷段>凸起段。 这说明上倾段为最难携液管段。
由图10 可以发现, 随着液量增加, 各管段持液率均增加。 其中液量在0.6 m3/h 处存在拐点,当液量大于0.6 m3/h 时, 持液率增加速率会急剧增加。 这说明管线此时液相含量增加, 积液程度会急剧增加, 因此现场集输管线应注意液量达到0.6 m3/h 后的集输管线运行状态。
由图11 可以发现: 凹陷段和凸起段均随着倾斜角度的增加持液率逐渐增大, 但变化趋势不明显; 对于上倾管路随着倾角增大会出现先减小后增大趋势, 这是因为角度小于6°时, 重力分量小,气体需克服的阻力较小, 随着角度继续增大, 重力分量变大, 此时气相能量不足以带走管内积液, 所以呈现持液率增大趋势。
综合以上分析可以得出, 在较小气量、 较大液量和较大倾斜角等导致积液的不利条件下, 上倾段和凹陷段最易出现积液, 在制定管线集输工艺参数时, 应重点考虑水平段和上倾段的临界携液能力。前面针对上倾斜管的室内研究能为临界携液流速的确定提供测试方法。
3.2 起伏管的压降分析
当液量为0.6 m3/h、 倾斜角为6°、 气量为20~200 m3/h 时, 管线总压降随气量的变化如图12 所示。
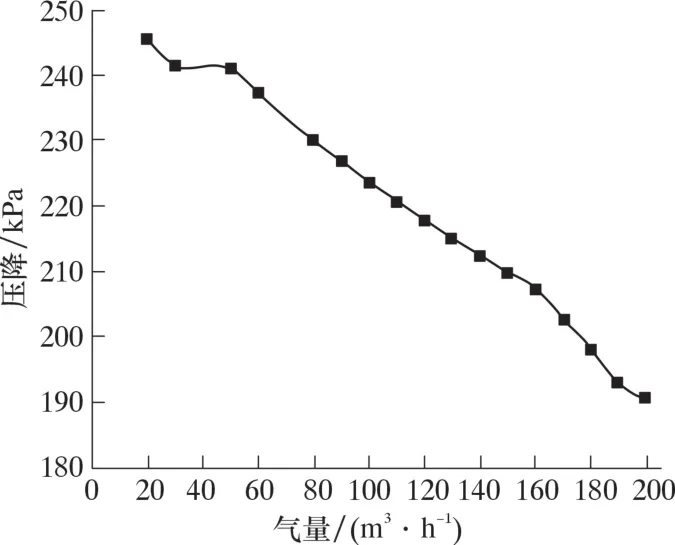
图12 压降随气量的变化Fig.12 Pressure drop vs. gas flow rate
由图12 可以发现, 随着气量的增加, 压降呈现出与倾斜管线不同的规律, 为持续下降。 这是因为压降主要由重位压降和摩阻压降组成, 当前气量范围下, 重位压降相较于摩阻压降占主导地位, 随着气量增加持液率减小, 重位压降逐渐减小, 因此总压降呈现减小趋势。 当气量为150 m3/h、 倾斜角为6°、 液量为0.1~2.0 m3/h 时, 压降随液量的变化如图13 所示。
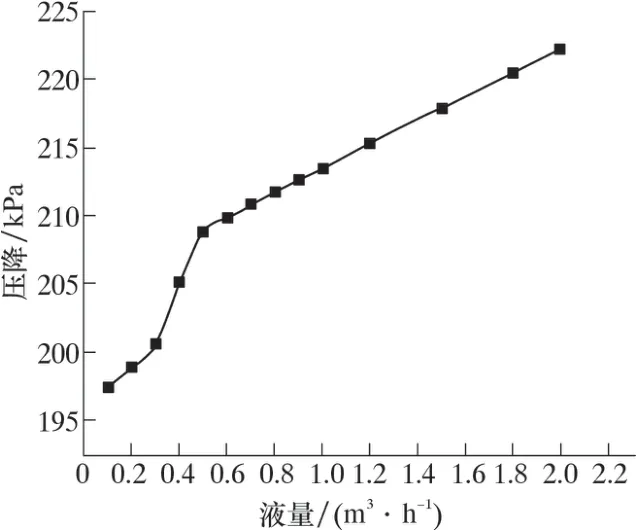
图13 压降随液量的变化Fig.13 Pressure drop vs. liquid flow rate
由图13 可以看出, 压降随着液量的增加不断增大, 当液量大于0.5 m3/h 时, 压降近似呈线性变化。 压降随倾斜角的变化如图14 所示。
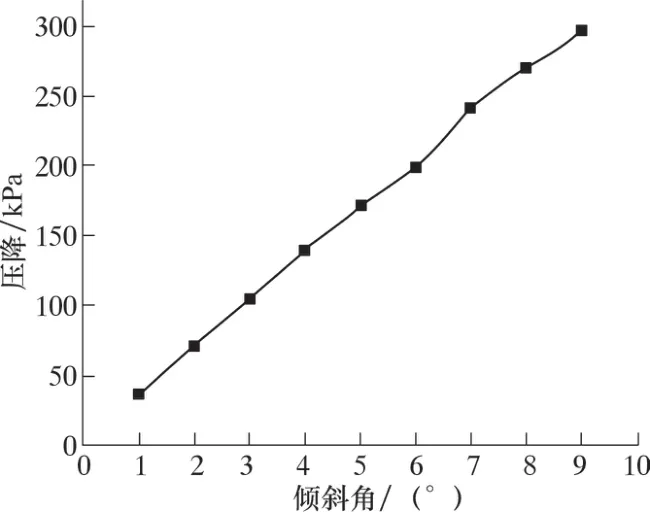
图14 压降随倾斜角度的变化Fig.14 Pressure drop vs. dip angle
由图14 可以看出, 压降随角度呈线性增加趋势, 这是因为当前角度范围内, 重位压降随着角度增加逐渐增大, 所以呈现出总压降逐渐增大趋势。
4 持液率模型建立
由于上倾段最容易积液, 所以对上倾段进行回归拟合持液率计算模型, 使其能准确预测起伏管路上倾段各个位置持液率。 本次回归以马克赫杰-布里尔计算方法为基础, 根据试验所测得的数据, 通过回归分析方法, 给出了气液两相持液率计算公式:
其中:
式中:vsl为液相的表观速度, m/s;vsg为气相的表观速度, m/s;σ为液相的表面张力, N/m;μl为液相的黏度, Pa·s;c1~c6均为经验常数, 详见表2。

表2 经验常数Table 2 Empirical constants
带入试验数据验证, 马克赫杰方法的计算误差普遍较大, 均在70%以上, 并且预测值普遍比实验值偏小。 表3 给出了马克赫杰试验与本试验主要条件参数。

表3 马克赫杰试验与本试验对比Table 3 Comparison between Mukherjee's experiment and this paper's experiment
由表3 可见, 2 种方法试验条件相差较大, 因此需要对参数进行重新拟合。
基于马克赫杰持液率相关式连续性较好、 考虑因素全面等优点, 选择对其关系式中的经验常数进行修正。 根据马克赫杰给出的气液两相流持液率关系式, 对试验的持液率Hl与马克赫杰给出的相关准数Nvl、Nvg、Nl的关系进行拟合。 经拟合得到新的经验常数和经修正后的持液率误差分别如表4所示。

表4 新的经验常数Table 4 New empirical constants
使用新的参数计算之后的各角度持液率平均误差见表5, 误差均在5%以内。

表5 不同角度修正后持液率计算平均误差Table 5 Average errors for liquid holdup corrected for different dip angles
5 结 论
本文基于起伏管路进行数值模拟和室内模拟试验研究, 得到以下结论:
(1) 通过对起伏管线进行数值模拟研究发现,凹陷段和上倾段极易积液, 且随着气量增大, 3 种管线持液率减小程度依次为: 凸起段>凹陷段>上倾段; 上倾管线中, 6°为持液率最低点, 此时液体最容易被带出; 上倾管线中, 压降随角度为线性增大。
(2) 通过室内试验发现, 35 ~70 m3/h 时携液量波动较明显, 此时易形成段塞流, 因此集输管线此工况下应注意段塞流对管线的损伤; 通对管路压降分析可得造成压力损失最大位置为凹陷管和凸起管处。
(3) 通过数值模拟结果与试验结果比对发现,模拟结果与试验结果非常接近, 这说明OLGA 软件计算的准确性较高; 基于马克赫杰-布里尔计算方法通过试验数据拟合得到适用于起伏管路上倾段的持液率预测式, 带入试验数据验证发现误差均在5%以内。

