不同人工晶状体屈光度计算公式在浅前房白内障患者中的准确性meta分析

李小禹 杨丽 海玥 谭青青 兰长骏 廖萱

川北医学院附属医院眼科 川北医学院眼视光医学院,南充 637000

眼球生物参数的准确测量和人工晶状体(intraocular lens,IOL)屈光度的精确计算是白内障术后获得良好视觉功能和视觉质量的关键[1]。近年来,光学相干生物测量逐渐取代了传统的超声生物测量,测量精度已得到大幅提升[2-3],IOL计算公式的准确性和公式选择的合理性成为影响IOL屈光度预测结果的主要原因。自20世纪70年代以来,各种IOL屈光度计算公式不断出现并用于临床实践,修正后的IOL计算公式准确性得以提高。引入有效晶状体位置(effective lens position,ELP)概念后,相继产生了以SRK/T、Holladay 1和Hoffer Q为代表的第3代理论计算公式,Haigis和Holladay 2为代表的第4代公式,以及目前临床开始使用的Barrett Universal Ⅱ公式,更有效地减小了白内障术后的屈光误差[4-8]。ELP主要受前房深度(anterior chamber depth,ACD)的影响,因此ACD在决定IOL计算公式的预测性中起着重要作用。既往研究发现,ACD、眼轴长度(axial length,AL)、角膜曲率(keratometry readings,K)分别可以解释42%、36%和22%的屈光误差[9]。在正常ACD下,各种IOL计算公式的准确性均较好;但随着ACD的减小,IOL计算公式屈光误差明显增加[10]。迄今已有多项研究比较了ACD对IOL屈光度计算公式的影响,然而结果仍存在争议[11-17]。本研究采用meta分析方法,系统评价IOL计算公式预测浅前房白内障患者术后屈光度的准确性,以期为临床选择提供循证医学证据。

1 资料与方法

1.1 文献检索策略

使用计算机检索外文数据库MEDLINE、EMBASE、Cochrane Library以及中文数据库中国知网、万方、维普数据库。使用以下检索式检索外文数据库:(“shallow anterior chamber depth *” OR “anterior chamber depth *” OR “shallow ACD” OR “ACD”) AND (“cataract” OR “IOL” OR “intraocular lens”) AND (“calculate *” OR “formula *”);使用以下检索式检索中文数据库:(“浅前房” OR “前房深度” OR “ACD”) AND (“白内障” OR “人工晶体” OR “人工晶状体” OR “IOL”) AND (“计算” OR “公式”)。检索语言限制为英文及中文,检索文献的起止时间为建库起至2020年8月。首先阅读所有检索文献的摘要,在排除明显不符合纳入标准的文献后,对可能符合纳入标准的文献进行全文阅读,根据预先拟定的文献纳入与排除标准确定最终纳入的文献。

1.2 文献纳入与排除标准

纳入标准:(1)研究类型为病例对照研究;(2)研究对象为接受常规白内障手术及IOL植入术的患者;(3)ACD <3.00 mm;(4)至少使用2种目标IOL度数计算公式;(5)眼部参数的测量均使用光学相干生物测量仪。排除标准:(1)复杂性白内障摘除手术或出现术中术后并发症;(2)既往有眼部手术史或外伤史,或患有其他可能影响视力的眼病;(3)Toric IOL、多焦点IOL及非囊袋内IOL植入;(4)未提供平均绝对误差(mean absolute error,MAE)作为结局指标;(5)无法获得全文。

1.3 数据提取及偏倚风险评估

由2位研究人员独立提取数据并将结果进行比较,通过与第3位研究人员讨论解决分歧。对重复发表研究,选择报告最全面、随访时间最长的资料数据。从纳入文献中提取以下资料:作者姓名、发表时间、基线特征(包括样本量、年龄、ACD、AL)、IOL类型、计算公式及其MAE、随访时间及术后验光方法。根据文献提供的原始数据进行计算,并提取MAE及标准差。采用改编自QUADAS-2工具的质量评价表,分别从偏倚风险和临床适用性2个方面对纳入文献中研究对象选择、IOL屈光度预测、术后验光方法、研究流程和进展进行评估[18]。纳入文献潜在的发表偏倚用漏斗图表示。

1.4 统计学方法

采用Revman 5.3软件进行结果数据的统计分析。计量资料MAE采用平均差(mean difference,MD)及其95%置信区间(confidence interval,CI)作为统计分析量,公式之间采用配对比较,P<0.05为差异有统计学意义。采用χ2检验判断各研究结果间的异质性,检验水准为α=0.1,同时结合I2值定量评价统计学异质性的大小。当I2值≤50%且P≥0.1时,使用固定效应模型;当I2值>50%且P<0.1时,应用随机效应模型,表明存在显著异质性,并进行敏感性分析和亚组分析以探讨可能的异质性来源。

表1 纳入研究的一般特征Table 1 Characteristics of included studies文献发表年份(年)人数/眼数年龄(x±s,岁)ACD(x±s,mm)AL(x±s,mm)IOL型号随访时间(周)验光方法IOL计算公式HaigisSRK/THoffer QHolladay 1Holladay 2Eom等[11]201453/5370.1±6.8<2.9021.69±0.29Acrysof IQ3-10客观验光√√Miraftab等[12]2014NA/10367.2±14.8<2.9022.91±0.65Acrysof SA60AT4NA√√√√Yang等[13]2017NA/7967.1±11.1<2.5023.93±1.46EC-1PAL12NA√√√√Gökce等[14]2018NA/10274.0±7.32.76±0.1823.62±0.53ZCB00、ZCT3NA√√√√邴丽英等[15]201845/4573.7±8.22.49±0.1723.15±0.54ZCB003-8主观验光√√√√Shrivastava等[16]201960/6061.6±9.42.44±0.1821.53±0.32Acrysof SN6CWS4NA√√√√√李娟等[17]202051/5765.6±7.8<3.0022.00-26.00Rayner 970C、920H4主观验光√√√√ 注:ACD:前房深度;AL:眼轴长度;IOL:人工晶状体;NA:未提及 Note:ACD:anterior chamber depth;AL:axial length;IOL:intraocular lens;NA:not available

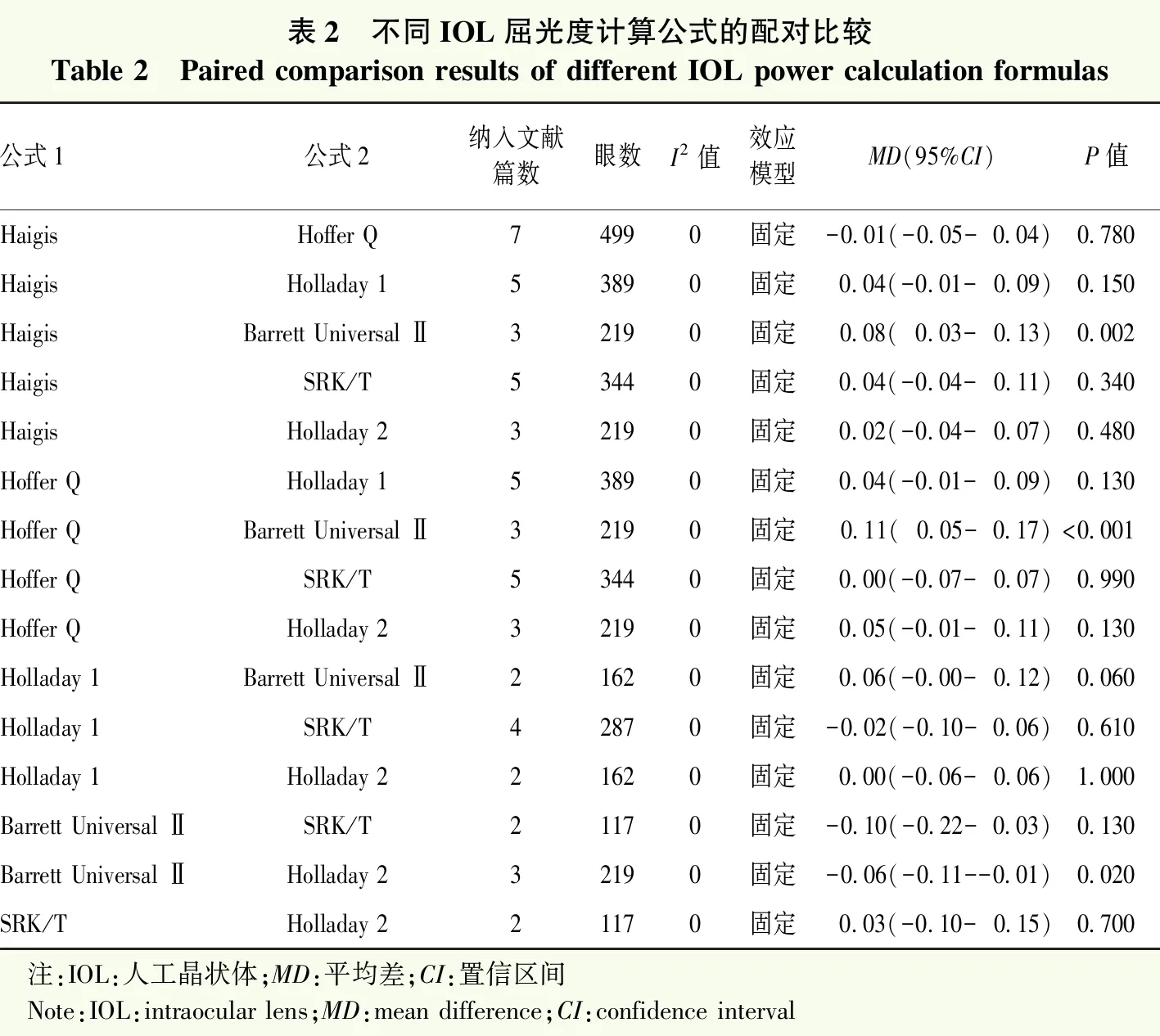
表2 不同IOL屈光度计算公式的配对比较Table 2 Paired comparison results of different IOL power calculation formulas公式1公式2纳入文献篇数眼数I2值效应模型MD(95%CI)P值HaigisHoffer Q74990固定-0.01(-0.05-0.04)0.780HaigisHolladay 153890固定0.04(-0.01-0.09)0.150HaigisBarrett Universal Ⅱ32190固定0.08(0.03-0.13)0.002HaigisSRK/T53440固定0.04(-0.04-0.11)0.340HaigisHolladay 232190固定0.02(-0.04-0.07)0.480Hoffer QHolladay 153890固定0.04(-0.01-0.09)0.130Hoffer QBarrett Universal Ⅱ32190固定0.11(0.05-0.17)<0.001Hoffer QSRK/T53440固定0.00(-0.07-0.07)0.990Hoffer QHolladay 232190固定0.05(-0.01-0.11)0.130Holladay 1Barrett Universal Ⅱ21620固定0.06(-0.00-0.12)0.060Holladay 1SRK/T42870固定-0.02(-0.10-0.06)0.610Holladay 1Holladay 221620固定0.00(-0.06-0.06)1.000Barrett Universal ⅡSRK/T21170固定-0.10(-0.22-0.03)0.130Barrett Universal ⅡHolladay 232190固定-0.06(-0.11--0.01)0.020SRK/THolladay 221170固定0.03(-0.10-0.15)0.700 注:IOL:人工晶状体;MD:平均差;CI:置信区间 Note:IOL:intraocular lens;MD:mean difference;CI:confidence interval

2 结果

2.1 纳入研究基本信息

初步筛选得到850篇文献,排除200篇重复文献,通过阅读摘要排除明显不符合纳入标准的620篇文献,全文阅读剩余的30篇文献;5篇文献ACD>3.00 mm,8篇文献仅包括1种目标IOL度数计算公式,10篇文献未提供MAE数据,最终纳入7篇文献(图1)。共纳入499眼,其中,Barrett Universal Ⅱ公式组219眼,Haigis公式组499眼,SRK/T公式组344眼,Hoffer Q公式组499眼,Holladay 1公式组389眼,Holladay 2公式组219眼(表1)。

图1 文献筛选流程图 IOL:人工晶状体;MAE:平均绝对误差

2.2 Meta分析

对Barrett Universal Ⅱ、Haigis、SRK/T、Hoffer Q、Holladay 1和Holladay 2进行配对比较,I2值均≤50%,说明统计学同质性好,均使用固定效应模型。Barrett Universal Ⅱ公式的MAE低于Haigis公式(MD:0.08 D;95%CI:0.03～0.13 D;P=0.002)、Hoffer Q公式(MD:0.11 D;95%CI:0.05～0.17 D;P<0.001)和Holladay 2公式(MD:-0.06 D;95%CI:-0.11～-0.01 D;P=0.020),差异均有统计学意义;其余公式之间的配对比较,差异均无统计学意义(均P>0.05)。预测误差在-0.50～+0.50 D的眼数百分比的比值比(odds ratio,OR),所有公式之间的配对比较差异均无统计学意义(均P>0.05)(表2,图2)。

图2 不同IOL屈光度计算公式配对比较的森林图 A:Haigis与Hoffer Q计算公式比较 B:Haigis与Holladay 1计算公式比较 C:Haigis与Barrett Universal Ⅱ计算公式比较 D:Haigis与SRK/T计算公式比较 E:Hoffer Q与Holladay 1计算公式比较 F:Hoffer Q与Barrett Universal Ⅱ计算公式比较 G:Barrett Universal Ⅱ与Holladay 2计算公式比较 CI:置信区间;SD:标准差

2.3 偏倚分析

采用改编自QUADAS-2工具质量评价表的评价结果显示,所有纳入文献均未说明患者的纳入是连续性还是随机性,存在未知偏倚;纳入文献中,有4篇文献纳入人群限定为正常AL患者(AL为22.00～25.00 mm),2篇文献纳入人群限定为短AL患者(AL<22.00 mm),因此对研究对象的选择存在一定偏倚;对于术后验光方法,大多数文献未说明是主观验光还是客观验光,因此存在未知偏倚。对于IOL屈光度预测和研究流程评估方面,大多数文献均为高质量。漏斗图结果显示各研究在图形上分布基本对称,提示发表偏倚较小(图3,4)。

图3 纳入文献基于改编自QUADAS-2工具质量评价表的评价结果 A:偏倚风险 B:临床适用性 IOL:人工晶状体

图4 发表偏倚漏斗图

3 讨论

临床研究表明,IOL计算公式在正常AL白内障患者中的准确性均较好,而在长AL和短AL患者中存在不同程度差异[19]。ELP概念引入IOL计算公式使得ACD备受关注,但研究发现AL与ACD间不存在线性正相关关系。Sedaghat等[20]在短AL(AL<22 mm)和长AL(AL>24.5 mm)患者中均未发现AL与ACD之间存在线性正相关关系。Chang等[21]在极长AL(AL≥27.5 mm)患者中也未发现AL与ACD间的线性相关性。本研究旨在评估不同IOL计算公式在浅前房白内障患者中的准确性。IOL计算公式的准确性通常用预测误差来衡量,即IOL计算公式的预测屈光度减去术后验光的等效球镜度数的差值;由于正负预测误差可以相互抵消,因此利用其绝对值的平均值MAE作为结局指标可判断IOL屈光度计算公式准确性,MAE越小,则预测屈光误差越小,术后裸眼视力越好,从而使患者获得更高的满意度。

本研究通过计算IOL屈光度计算公式的MAE来评估其预测浅前房白内障患者屈光度的准确性,结果表明在浅前房白内障患者中,Barrett Universal Ⅱ公式优于Hoffer Q、Haigis和Holladay 2公式,差异均有统计学意义,提示Barrett Universal Ⅱ公式对浅前房患者IOL屈光度预测的影响最小,术后屈光误差较低,预测准确性较高。Hipólito-Fernandes等[22]对237例浅前房(ACD<3.00 mm)白内障患者进行研究发现,Barrett Universal Ⅱ的预测准确性较Hoffer Q公式高。此外,Melles等[23]对超过18 000例白内障患者进行研究发现,当ACD<3.00 mm时,Barrett Universal Ⅱ公式对IOL屈光度的预测误差小于Hoffer Q、SRK/T、Haigis、Holladay 1和Holladay 2公式,与本研究结果基本一致。Hoffer Q公式是几何光学原理推导的理论公式和经验回归公式的结合,利用AL及K正切值来预测术后ELP。由于Hoffer Q公式根据薄透镜原理,在正常模拟眼参数基础上进行公式的运算,故对于前房较浅的患者,ACD与AL不成比例,可能会导致IOL度数的预测误差。Haigis公式假定术后ELP是a0、a1、a23个常数的函数,即ELP=a0+(a1×ACD)+(a2×AL),其中a0可由IOL A常数推导而来,a1为ACD常数,a2为眼轴常数,需要通过对临床回顾性研究进行线性回归分析,从而不断对常数进行优化[24]。

Holladay 2公式是应用范围较广的公式之一,然而最近的研究发现Barrett Universal Ⅱ的预测准确性比Holladay 2公式更高。Kane等[25]对3 214例白内障患者进行研究发现,Barrett Universal Ⅱ公式对长、中、短AL的MAE预测小于Holladay 2公式。Cooke等[26]分别应用部分相干干涉和光学低相干反射生物测量仪对患者眼部参数进行测量,结果显示Barrett Universal Ⅱ公式的预测误差均小于Holladay 2公式。Kim等[27]采用扫频光学相干断层扫描生物测量仪对324例白内障患者进行研究也发现,Barrett Universal Ⅱ公式比Holladay 2公式有更高的预测准确性。本研究结果显示,在浅前房白内障患者中,Barrett Universal Ⅱ公式的MAE低于Holladay 2公式,在多变量公式中Barrett Universal Ⅱ公式的准确性较高。Barrett Universal Ⅱ公式预测术后ELP使用5个参数,包括AL、K、ACD、晶状体厚度(lens thickness,LT)和角膜直径,根据厚晶状体模型和近轴光线追踪原理进行IOL屈光度数计算,考虑了不同屈光度IOL所遇到的主平面变化[28]。Holladay 2公式是在原始Holladay公式基础上改进而来,考虑了上述5个变量以及术前屈光状态和年龄[29]。Srivannaboon等[30]的研究显示,未纳入LT的Holladay 2公式与纳入LT的Holladay 2公式的预测准确性差异无统计学意义;此外,Mahdavi等[31]发现在影响Holladay 2公式术后屈光误差的7个变量的相对重要性中,LT位居倒数第2,提示LT值在Holladay 2公式中的作用较弱,可能影响晶状体较厚的浅前房白内障患者的IOL屈光度预测。

Holladay 1和SRK/T公式均以第1代理论公式Fyodorov为基础,利用AL和K值来预测术后ELP。其中,Holladay 1公式ELP是指角膜厚度、角膜高度(角膜内皮到虹膜前表面的距离)与虹膜前表面到IOL主平面距离的总和,SRK/T公式ELP是指角膜到虹膜平面的距离与补偿函数之和;SRK/T公式还结合了大量患者术后屈光结果,对角膜屈光系数、ACD、视网膜厚度等进行修正。第3代IOL计算公式Holladay 1和SRK/T公式均未考虑术前ACD对术后ELP的影响,并不使用ACD的实际测量值,而是假设ACD与AL有关,即短AL患者前房较浅,长AL患者前房较深。然而,80%的短AL患者在白内障及IOL植入手术后有正常的前房解剖结构[32],因此,以Holladay 1和SRK/T公式预测浅前房白内障患者IOL屈光度可能产生较大误差。但是本研究结果未发现Barrett Universal Ⅱ公式与Holladay 1公式和SRK/T公式之间MAE差异有统计学意义,分析可能与Barrett Universal Ⅱ公式目前在临床应用时间不长、相关研究样本量较小有关,故对这一结果的解释需谨慎,有待更多大样本量的研究进一步探索。

本研究仍存在一定的不足:由于浅前房白内障患者在人群中所占的比例较低,本研究纳入的研究文献数量及病例数量有限;Barrett Universal Ⅱ公式相关的临床研究较少因而纳入样本量较小,与其他公式进行比较时统计学效应可能不足;未考虑患者的AL、IOL类型,而这些因素可能会影响IOL屈光度计算公式的准确性;受研究方法学所限,缺乏充分的随机对照试验数据,可能会降低研究的质量。除此之外,各种新型IOL计算公式也在不断地推出并显示良好的前景,例如基于光线追踪技术的Olsen公式、基于人工智能的Hill-RBF公式等,但由于其在临床中应用时间较短,尚缺乏相关研究文献,故未被纳入到本研究中。

综上所述,本研究结果显示在浅前房白内障患者中,Barrett Universal Ⅱ公式在预测IOL屈光度方面优于Hoffer Q、Haigis和Holladay 2公式,对于浅前房的患者可考虑应用Barrett Universal Ⅱ公式以减少屈光误差。

利益冲突所有作者均声明不存在利益冲突

作者贡献声明李小禹:研究设计和实施、数据采集和分析/解释、论文撰写;杨丽、海玥:实施研究、采集数据;谭青青、兰长骏:审阅和修改论文;廖萱:研究设计、数据分析、论文修改、对文章知识性内容作批评性审阅