一种基于航向估计的多平台纯方位目标转向机动检测算法
李岩昊,袁富宇
(江苏自动化研究所,江苏 连云港 222061)
纯方位目标跟踪(Bearing-Only Tracking, BOT)是通过观测到的目标方位序列估计目标状态[1],在军事领域和民用领域发挥着重要作用,例如水下监视[2]、空中目标跟踪以及无人机(UAV)路径规划[3-4]。
针对BOT领域,国内外学者对跟踪模型以及非线性滤波两个方面进行了广泛研究。在建立跟踪模型研究方面,Bar-Shalom等人基于广义伪贝叶斯(GPB)算法[5],提出了一种通过马尔可夫状态转移矩阵来进行模型交互的交互多模型算法(Interactive Multiple Model, IMM)[6],相较于单一模型,该算法能够有效跟踪机动形式多变的目标,但存在自适应能力较差的问题。X R Li等人在此基础上做出改进,提出了基于可变模型集的变结构多模型算法(Variable Structure Multiple Model, VSMM)[7],该算法能够在跟踪过程中自适应调整模型集,提高了跟踪效率。在处理非线性滤波问题方面,有基于贝叶斯滤波的Kalman滤波及其改进算法[8-10],但这类滤波器对初值选取敏感,容易产生滤波发散的问题。粒子滤波算法[11-12]是通过蒙特卡洛方法来求解贝叶斯估计中的最优估计,在非线性、非高斯系统中被广泛应用,但系统的后验概率密度需要通过选取大量样本来近似,导致算法复杂度高,不宜应用于复杂多变的跟踪场景。此外,其他学者所提出的基于方位预测误差序列均值变化的重复利用序列概率比检测[13-14]、批处理方法如Taylor级数法[15-16]、最小二乘法[17-18]和极大似然估计[19]等算法,给BOT问题的研究提供了更加多元化的思路。Taylor级数要素解算法迭代收敛速度快,跟踪远距离匀速直航目标时截断误差小[15],被应用到各种被动定位系统中。
本文以Taylor级数要素解算为基础,针对目标转向机动,提出了基于两段运动要素联合解算、两段运动要素独立解算两种解算模型以及基于估计相邻段航向差序列的机动检测算法,并对机动时刻进行估计。仿真结果表明,两种解算模型下的机动检测算法能够有效地对转向机动目标进行机动检测。
1 基于双平台Taylor级数要素解算
水下双平台观测形式如图1所示,平台1、平台2坐标为(xo,1,yo,1),(xo,2,yo,2),目标在机动前tk时刻的运动状态为
Xk=(xk,yk,VTx,VTy)′+Wkk=1,…,n
(1)
其中,(xk,yk)′为目标的位置坐标,(VTx,VTy)′为目标的速度分量(假定目标转向机动前匀速直航),Wk为过程噪声:Wk=(wx,k,wy,k,wVTx,k,wVTy,k)′k=1,…,n。
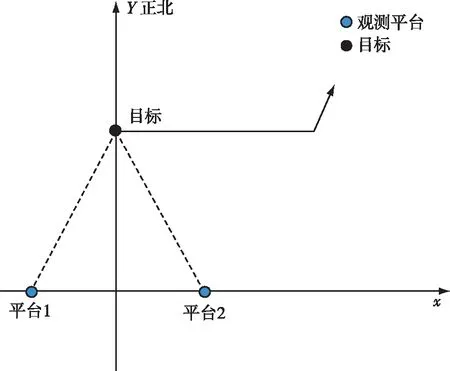
图1 双平台观测Fig.1 Dual-platform observation
目标位置与速度的关系为:
xk=x0+VTx·Δtkk=1,…,n
(2)
yk=y0+VTy·Δtkk=1,…,n
(3)
(x0,y0)′为目标初始位置坐标,Δtk为初始时刻到tk时刻的时间间隔,tk=tk-t0,k=1,…,n,(wx,k,wy,k)′,(wVTx,k,wVTy,k)′为过程噪声的距离分量和速度分量,取其为高斯白噪声,过程噪声距离分量与过程噪声速度分量的关系为wx,k=(wVTx,1+…+wVTx,k)·Δt,wy,k=(wVTy,1+…+wVTy,k)·Δt,k=1,…,n。Δt为采样间隔,由于位置坐标可由(2)、(3)式推算出来,解算的目标运动要素为
X0=(x0,y0,VTx,VTy)′
(4)
平台1、平台2的方位序列量测方程为

(5)
(xk-1+wx,k-1,yk-1+wy,k-1)为目标在tk-1时刻的位置,经化简后,(5)式等价于

i=1,2k=1,…n
(6)
其中,σBi,k为量测噪声,φBi,k为体现在量测方位上的过程噪声,给定初值X0,对两平台观测方位在X0处进行一阶Taylor展开:
Bi,k≈Bi,k(X0)+Bi,k(X0)·dX+φBi,k+σBi,k
i=1,2k=1,…n
(7)
其中,
dX=X-X0
(8)
i=1,2k=1,…n
(9)
将(6)式代入(9)式中,得

(10)

令
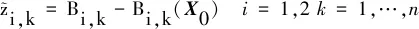
(11)
Hi,k=Bi,k(X0)i=1,2k=1,…,n
(12)
则(7)式可改写为
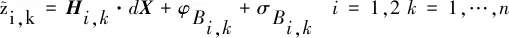
(13)
(13)式就转化为最小二乘滤波问题,采用线性加权最小二乘法可证:
i=1,2k=1,…,n
(14)
更新迭代:
X1=X0+dX
(15)
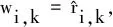
2 基于相邻段航向差序列的目标机动检测
目标机动形式为转向机动。目标在机动时刻前后匀速直航,量测方位噪声是高斯白噪声。
2.1 两段运动要素联合解算
假设目标发生转向机动,机动时刻未知,目标机动前后运动要素联合解算模型如下:
令机动前后目标速度为:V1=(VTx1,VTy1)′,V2=(VTx2,VTy2)′,机动时刻为tm,需要解算的目标运动要素由(4)式中的四维矢量扩维成六维矢量:
X=(x0,y0,VTx1,VTy1,VTx2,VTy2)′
(16)
叠加过程噪声后,目标相对于两平台的方位序列量测方程
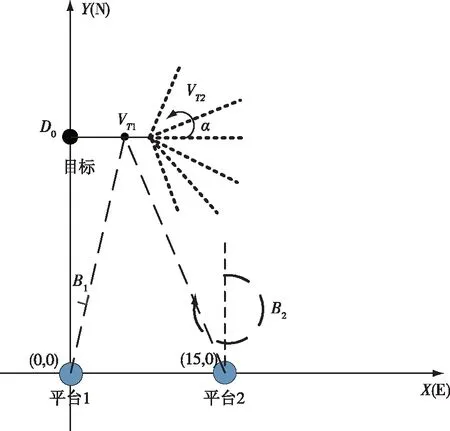
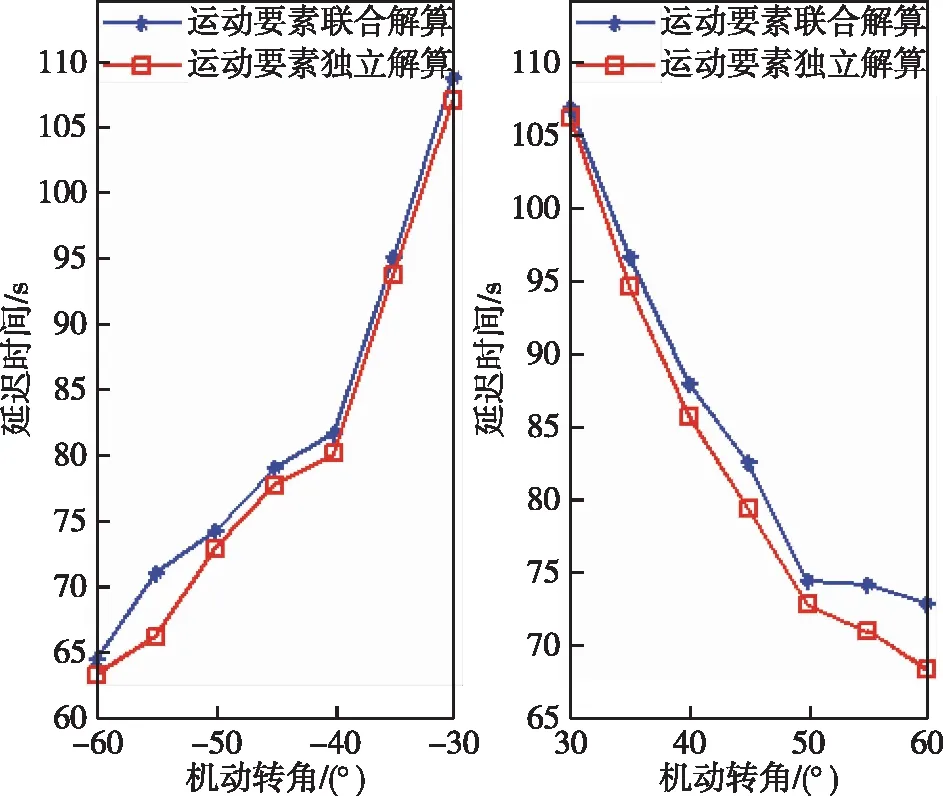
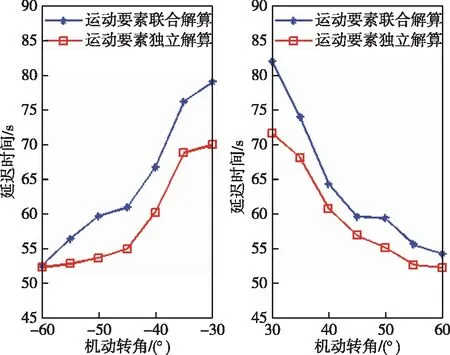
i=1,2k=1,…,n;tk (17) (18) 其中,Δtk=tk-t0,Δt1k=tm-t0,Δt2k=tk-tm,机动时刻前,(10)式改为 (19) 机动时刻后,(9)式改为 (20) 对于目标机动前后的要素解算,另一种方法是把机动前段和机动后段独立出来,首先估计出目标机动前的状态,推算出目标在发生机动时的状态(位置和速度),作为机动后段的初始状态,再对机动后段进行独立解算。目标机动前的初始状态为 X1=(x0,y0,VTx1,VTy1)′ (21) 目标机动后的初始状态为: X2=(xm,ym,VTx2,VTy2)′ (22) xm=x0+VTx1·(tm-t0) (23) ym=y0+VTy1·(tm-t0) (24) 其中,tm为机动时刻,(xm,ym)′为待估计的目标在第2段的初始位置。 本论文探讨的机动检测法是基于航向差序列变化进行分析的,假定目标匀速直航或进行转向机动,但机动时刻tm未知,如图2所示。 图2 机动时刻未知的目标航路Fig.2 Unknown-maneuvering target situation (25) 其中,β表示航向差门限,g0表示置信水平门限。N(|ΔCTl|>β)表示航向差绝对值大于门限β的对应的假定机动点个数。 (26) (27) (28) 考虑如下评价指标: 2)虚警率:把目标的匀速直航检测成机动的概率,计算模式同1)。 3)机动时刻的估计精度:在正确检测的条件下,统计估计机动时刻的精度,用估计机动时刻均方误差σΔtm表示。 4)机动检测延迟时间:是指检测到目标机动的时间与实际目标发生机动的时间差,用均方误差σΔ(tk-tm)表示,其中,tk表示检测到机动的当前时刻。 以大地直角坐标系为例,观测平台1、平台2坐标设为P1(0,0),P2(15,0)(单位:km),目标初始位置(0,D0)(下文用目标初距D0表示);目标机动前的速度为VT1,机动后的速度为VT2;目标机动前的航向为CT1,机动后的航向为CT2,机动转向角α(顺时针为正,逆时针为负);过程噪声φB,量测噪声σB;两平台量测到的方位角B1、B2如图3所示(图3假设目标初始航向为90°);取β=10°,g0=75%,采样间隔为1 s,量测噪声σB=1°,过程噪声φB=1 kn,噪声类型均为高斯白噪声,目标机动方式为转向机动。 仿真计算航路参考数值如表1所示,共有3×3×3×5×10=1 350种组合: 图3 目标航路Fig.3 Target situation 表1 仿真参考数值 迭代初值选取:目标初距D0在(6,30)km区间内随机选取,速度VT1在(8,30)节内随机选取,初始舷角QT在(-180°,180°)内随机选取。 1)匀速直航虚警率 以目标初始航向90°,目标速度18 kn,目标初始位置分别为30、40、50(单位:km),量测噪声σB=1°,过程噪声φB=1 kn,目标总航行时间12 min,算法分别在T=5 min、T=6 min、T=7 min时刻启动,对目标进行转向机动检测。每组航路仿真10 000次,统计目标匀速直航时基于双平台Taylor级数要素解算算法的迭代收敛次数、基于两种解算模型的目标机动检测算法的虚警率。迭代收敛依照(13)式中‖dX‖2<10-7来判断,表2为统计结果。 目标匀速直航时,对于目标初始距离30 km、速度18 kn、量测噪声1°、过程噪声1 kn的航路下,解算10 000 次航路,结果全部迭代收敛,算法的虚警率为0%,随着目标初始距离增大,两种解算模式下的机动检测算法均出现虚警,且虚警率与算法启动时刻相关,以目标初距50 km的航路为例,算法启动时刻T=5 min、T=6 min、T=7 min时,联合解算对应的机动检测虚警率分别为15.11%、9.25%、6.25%;独立解算对应的机动检测虚警率分别为7.69%、6.69%、4.69%。原因是算法启动时间越长,收集的量测数据越多,解算精度越高,虚警率越低。 2)机动检测率 为验证算法对于机动角度的适应范围,统计在仿真航路参数范围内目标机动检测延迟时间,包括在目标机动后两分钟内以及机动后三分钟内的机动检测率,其中目标机动时刻tm=6 min,目标总观测时间tn=12 min。算法启动时刻T=6 min。机动转角α在15°~60°范围内选取。表3为统计结果。 表2 匀速直航解算虚警率Tab.2 Convergence and false alarm rate of constant speed direct flight 表3 不同机动转角下目标机动检测率Tab.3 Target maneuver detection rate at different maneuvering angles 在机动转角大于等于30°的航路下,两种解算模型下算法在机动后两分钟内的机动检测率大于90°。仿真结果表明算法适用于机动转角大于等于30°的航路。 3)航路参数对机动检测结果影响 统计目标转向机动时,目标初始位置、目标速度、机动转角大小对目标机动检测延迟时间和目标机动时刻估计精度的影响。 图4、图5表示目标初始距离对两种解算模型下机动检测算法的机动检测延迟时间和机动时刻估计精度的影响,对应仿真的目标航路参数:目标初距D0在(30,50)km范围变化,目标速度18 kn、机动转角45°、初始弦角90°、量测噪声σB=1°;过程噪声φB=1 kn。 图4 目标初距对机动检测延迟时间的影响Fig. 4 Influence of target initial distance on the delay time of maneuver detection 图5 目标初距对机动时刻估计精度的影响Fig. 5 Influence of target initial distance on the accuracy of maneuvering time estimation 图6、图7表示目标速度对两种解算模型下机动检测算法的机动检测延迟时间和机动时刻估计精度的影响。对应仿真的目标航路参数:目标速度VT1、VT2在(10,24)kn范围变化,目标初距为30 km,机动转角45°,初始弦角90°,量测噪声1°,过程噪声1 kn。 图6 目标速度对机动检测延迟时间的影响Fig. 6 Influence of target speed on maneuver detection delay time 图8、图9表示机动转角对两种解算模型下机动检测算法的机动检测延迟时间和机动时刻估计精度的影响。对应仿真的目标航路参数:机动转角α在(-60°,60°)内范围变化,目标初距30 km,目标速度18 kn,初始弦角90°,量测噪声1°,过程噪声1 kn。 图8 机动转角对机动检测延迟时间的影响Fig. 8 Influence of maneuver angle on maneuver detection delay time 目标航路对机动检测算法的影响主要表现在:随着目标与观测平台初始距离增大,机动检测延迟时间增大,且出现虚警,同时,机动时刻估计精度降低;随着目标速度降低,观测到的方位序列变化不明显,这导致目标机动检测时间增大,机动时刻估计精度降低。目标转向方向同样对机动检测结果存在影响,图9中,左舷侧机动和右舷侧机动时,机动时刻估计结果相差较大,尤其是正负30°转角处相差最大。这是由于在向右舷侧转向机动时,目标靠近观测平台,相对于观测平台的距离更近,方位变化明显;目标向左舷侧转向机动则远离观测平台,方位变化并没有右舷机动明显,为验证这一观点,选定对称航路进行仿真实验,令目标初始位置位于观测平台中央,即目标初始位置(x0,y0)=(10,30)km,目标机动前后速度VT1=VT2=18 kn,初始航向CT1=180°,过程噪声фB=1 kn,量测噪声σB=1°,机动时刻tm=6 min,统计机动转角|α|=30°~60°时,机动检测延迟时间和机动时刻估计精度。每组航路仿真10 000 次,机动检测结果图10、图11所示。 图10 机动转角对机动检测延迟时间的影响Fig.10 Influence of measurement error on the delay time of maneuver detection 图11 机动转角对机动时刻估计精度的影响Fig.11 Influence of measurement error on the accuracy of maneuvering time estimation 仿真结果表明,对称航路下,左舷机动和右舷机动检测结果大致相同,二者的机动检测延迟时间均低于90 s,机动时刻估计精度均低于15 s。 本文针对纯方位条件下的变向机动目标,根据目标航向变化规律进行机动检测,基于反推方位均方误差进行机动时刻估计。该算法针对目标初距30~50 km、速度10~25 kn,过程噪声速度分量1 kn,量测噪声1°,转向角不小于30°的航路,算法全部迭代收敛,机动检测延迟时间在2 min以内,机动时刻估计误差小于60 s,机动检测算法的虚警率低于10%,仿真结果表明该算法可以有效地对水面及水下转向机动目标进行机动检测及跟踪。

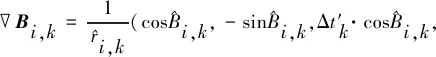
2.2 两段运动要素独立解算
2.3 纯方位目标机动检测


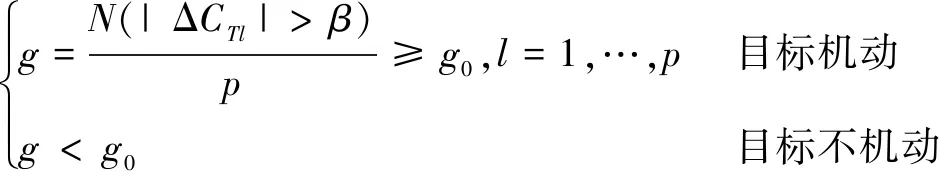
2.4 机动时刻估计





3 仿真分析
3.1 评价指标
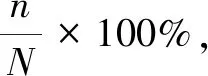
3.2 算例航路参数

3.3 仿真结果及分析






4 结束语

