一种改进的主从式协同导航技术研究

陈东隅

(江苏自动化研究所,江苏 连云港 222061)

利用水面无人艇编队参与区域搜救、反潜等特殊任务时,需要多艘无人艇之间相互协同作业才能完成任务。但在复杂的战场环境下,各种针对卫星导航系统的干扰和拒止手段层出不穷,各无人艇仅依靠自身搭载的惯性组件,其导航定位精度很难满足协同作业的发展需求,因此,如何让无人艇编队在卫星导航信号拒止环境下长时间保持良好的导航定位精度,是遂行相关任务的关键[1-2]。

近年来,国内外研究人员对于陆上机器人、水下自主潜航器和无人机的协同导航定位技术研究较为深入[3-5]。美国明尼苏达大学的S.I.Roumeliotis等人对机器人协同导航进行了研究,提出了一种新颖的分散式协同导航算法,使用基于卡尔曼滤波的算法来实现协同定位[6];2016年,欧洲多家科研单位在欧盟的资金支持下开展了名为MORPH的研究项目,该项目对多个AUV进行协调作业时的系统结构和通信问题进行了研究,并完成了基于多AUV系统的协调控制和协同定位等多项技术的试验验证[7]。

目前,对于水面无人艇编队的协同导航研究尚处于起步阶段,其中,主从式协同导航技术是该领域的重要研究方向[8],其分为单主艇和多主艇两种技术途径。无人艇可通过自身搭载的光电、雷达、水声或无线电测距等设备获取相对其他无人艇的距离信息和方位信息等,再利用无线通信交换各自的运动状态信息进行协同导航定位,从而提高自身的导航定位精度[9]。

本文以一艘搭载高精度组合导航设备或能够正常获取卫星导航信号的无人艇作为主艇,其他搭载廉价的低精度惯导组件的无人艇为从艇,组成了单主多从的无人艇编队。其中,主艇的高精度定位信息在无人艇编队中可以实时共享。在传统的单主多从协同导航系统中,各从艇仅与主艇建立关系,独立解算自身的位置信息。本文将任意两艘从艇与主艇组成了改进的主从式协同导航系统,通过测量并共享三者间的距离改正从艇的位置,最终提高编队中从艇的导航定位精度。该方法避免了在每艘无人艇上都安装价格昂贵的高精度导航设备,减小了无人艇编队的成本,且相比传统方法可进一步抑制误差累积速度,提升导航定位精度。

1 改进的主从式协同导航算法

1.1 基本原理

无人艇编队在卫星导航信号拒止环境下进行航位推算时,由于受惯导组件误差特性影响,导航定位时会随着时间推移产生较大的累积误差。本文中的无人艇编队包含1艘主艇和2艘从艇,从艇均处于卫星导航信号拒止区域。无人艇编队的运动过程可看作二维平面运动,可忽略高程因素,分别将主艇Μ和从艇Α、Β的位置记为PM=(xM,yM)、PA=(xA,yA)和PB=(xB,yB)。本文认为主艇的位置是包含高斯噪声的准确位置。而从艇在卫星导航信号拒止环境下,仅依靠自身搭载的低精度惯性导航组件进行航迹推算,则从艇A和B的航迹推算模型可表示为

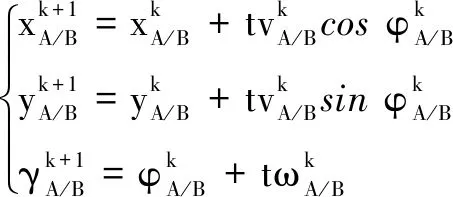
(1)

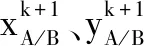
传统的主从式协同导航方法中,从艇通过无线网络实时获取主艇的精确位置,再利用测距设备获取与主艇之间的相对距离,最终通过与本艇运动状态信息的融合滤波计算出该时刻的位置,提高了从艇导航定位精度。

改进的主从式协同导航算法在此基础上,引入从艇之间的测距信息作为一种误差约束条件,使得基于EKF的主从式协同导航技术在一主多从的应用场景中,导航定位精度得到进一步提高。

改进的主从式协同导航定位原理如图1所示。

图1 改进的主从式协同导航原理Fig.1 Principle of the improved leader-follower cooperative navigation

主艇在k时刻的运动状态(包括位置、速度、加速度、航向角等)以及与从艇之间的相对距离可实时广播至各从艇,将主艇与从艇、从艇与从艇间测距信息以及各艇的运动状态进行融合解算,即构建相应的运动方程和量测方程进行扩展卡尔曼滤波,可有效抑制从艇的航迹误差随时间增加的速率,提升从艇的导航定位精度[10]。改进的算法中增加了从艇间的测距信息,且该信息较为精准,因此,在融合计算时,可以将两艘从艇的位置误差约束在一定范围以内。

图1中虚线圆圈表示从艇航迹推算误差,斜纹圆圈表示采用传统主从式协同导航后的航迹误差,深灰色圆圈表示增加了从艇间距离观测量后进行滤波计算的误差。可以发现,随着已知条件的增加,从艇的导航定位精度改善较为明显。

1.2 数学模型

本文针对1艘主艇和2艘从艇组成的协同导航系统建立离散非线性系统状态方程如下:

Xk+1=f(Xk,μk,υk)=Xk+Γ(μk+υk)

(2)

(3)

在此应用场景下,主艇和从艇以及从艇和从艇之间的距离观测量组成的量测方程Zk可表示为

(4)

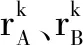
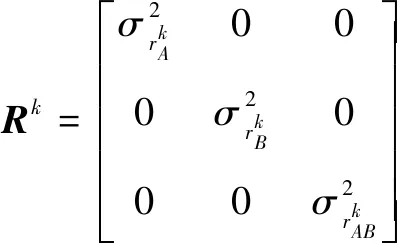
(5)

1.3 模型的线性化及滤波过程

由式(2)和式(4)可知,系统的状态方程和量测方程均包含非线性项,卡尔曼滤波(KF)一般只针对线性系统,因此,本文采用扩展卡尔曼滤波(EKF)对以上系统进行滤波[11]。根据EKF算法,首先分别围绕状态向量Xk和控制向量μk将系统的状态方程非线性部分进行泰勒级数展开:

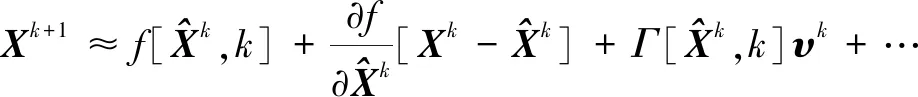
(6)

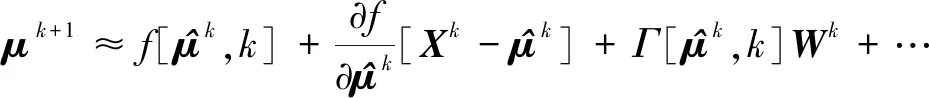
(7)

将状态方程的泰勒级数展开式略去二阶以上的高阶项,则f(Xk,μk,υk)关于状态向量Xk和控制向量μk的雅可比矩阵(Jacobian)分别为:

(8)

(9)

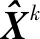
(10)

将量测方程的泰勒级数展开式略去二阶以上的高阶项,则量测方程关于状态向量Xk的雅可比矩阵H可表示为

(11)

对系统线性化后的运动模型应用卡尔曼滤波基本方程可得到扩展卡尔曼滤波递推方程,其具体步骤如下:

1)系统状态一步预测

(12)

2)系统一步预测的协方差矩阵

Pk+1,k=FkPk(Fk)T+UkQk(Uk)T

(13)

式中,Pk为从艇运动状态的协方差阵,Qk为系统过程噪声协方差阵,Fk和Uk分别为系统状态方程的雅可比矩阵。

3)滤波增益

Kk+1=Pk+1,k(Hk+1)T(Hk+1Pk+1,k(HK+1)T+Rk+1)-1

(14)

式中,Rk+1为量测误差矩阵,Hk+1为量测方程的雅可比矩阵。

4)系统状态估计

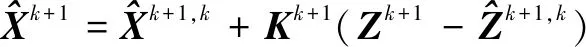
(15)

5)系统状态估计误差的协方差阵更新

Pk+1=Pk+1,k-Kk+1Hk+1Pk+1,k

(16)

以上就是扩展卡尔曼滤波器的一个计算周期,各个时刻EKF对主从式协同导航系统的处理就是这个周期不断重复的过程。

1.4 系统误差源分析

改进的主从式协同导航系统的误差主要来源于以下几个方面:

1)主艇和从艇本身的运动状态误差,即主从艇本身的航行位置、速度、加速度和航向角等产生的误差。其中,主艇的位置误差包含艇载的高精度导航定位设备误差(可优于米级)以及无人艇受航行控制系统和水文条件等因素影响产生的航行控制误差[12]。

2)主从艇之间的测距误差,即主艇与从艇间的测距以及从艇与从艇间的测距误差。目前,艇间距离测量可采用激光测距、水声测距或者雷达测距等手段完成,但随着艇间距离逐渐增大,测距误差也逐步增大[13]。

3)信息传输时延误差。由于各观测量均通过无线网络传输并进行计算,在传输过程中存在一定的网络时延,解算的定位结果与实际位置存在误差。本文假设所有数据都是实时获取和处理的,暂不讨论信息传输时延产生的误差。

4)数学模型误差。由于系统状态方程和量测方程在线性化过程中省略了高阶项,从而产生了计算误差。本文仅讨论主从艇以固定航向进行的匀速直线运动,相应的运动方程不属于高度非线性系统,因此,在线性化过程中,略去的高阶项产生的系统误差可以忽略。

2 仿真结果分析

为验证改进的主从式协同导航算法相比于传统方法对从艇导航定位误差的抑制效果,本节进行了仿真计算。

1艘主艇和2艘从艇在编队航行时,进入卫星导航信号拒止区域,主艇和从艇相互之间保持一定的距离,且主从艇之间具备无线网络通信及相互观测的条件。设定主艇和从艇的仿真条件如表1所示。

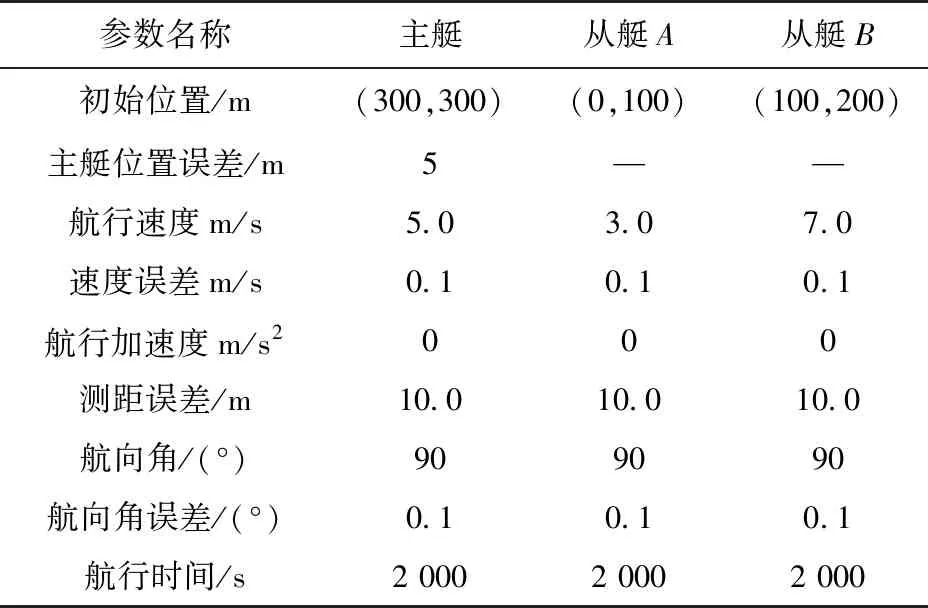
表1 仿真实验参数Tab. 1 Parameters of the simulation experiment

主艇和从艇A、B按照表1中设定的参数航行约2 000 s,其中,主艇航速约10 kn,从艇A航速约6 kn,从艇B航速约14 kn,不考虑水流、风速等环境因素的影响,三艘艇航行的实际轨迹如图2所示。

图2 主艇和从艇A、B真实航行轨迹图Fig.2 Real route of leader boat and follower boats

图2中,黑色线段表示主艇实际航行轨迹;红色线段表示从艇A的航行轨迹;蓝色线段表示从艇B的航行轨迹。

现分别对从艇A和从艇B采用传统的主从式协同导航方法解算各自的航行轨迹,如图3和图4所示。

图3a)和图4a)中,黑线分别表示从艇A、B的实际航行轨迹;红线分别表示航迹推算轨迹;蓝线分别表示采用传统的主从式协同导航算法,从艇A、B的航行轨迹。图3b)和图4b)中,黑色线段表示从艇A、B的航迹推算误差,红色线段表示协同导航后的航迹误差。可以看出,传统的主从式协同导航技术可在一定程度上抑制从艇的导航定位误差。

这里采用以上改进的协同导航算法,对于一艘主艇多艘从艇的协同导航情况,任意选取两艘从艇之间的测距信息进行融合解算,仿真结果如图5和图6所示。

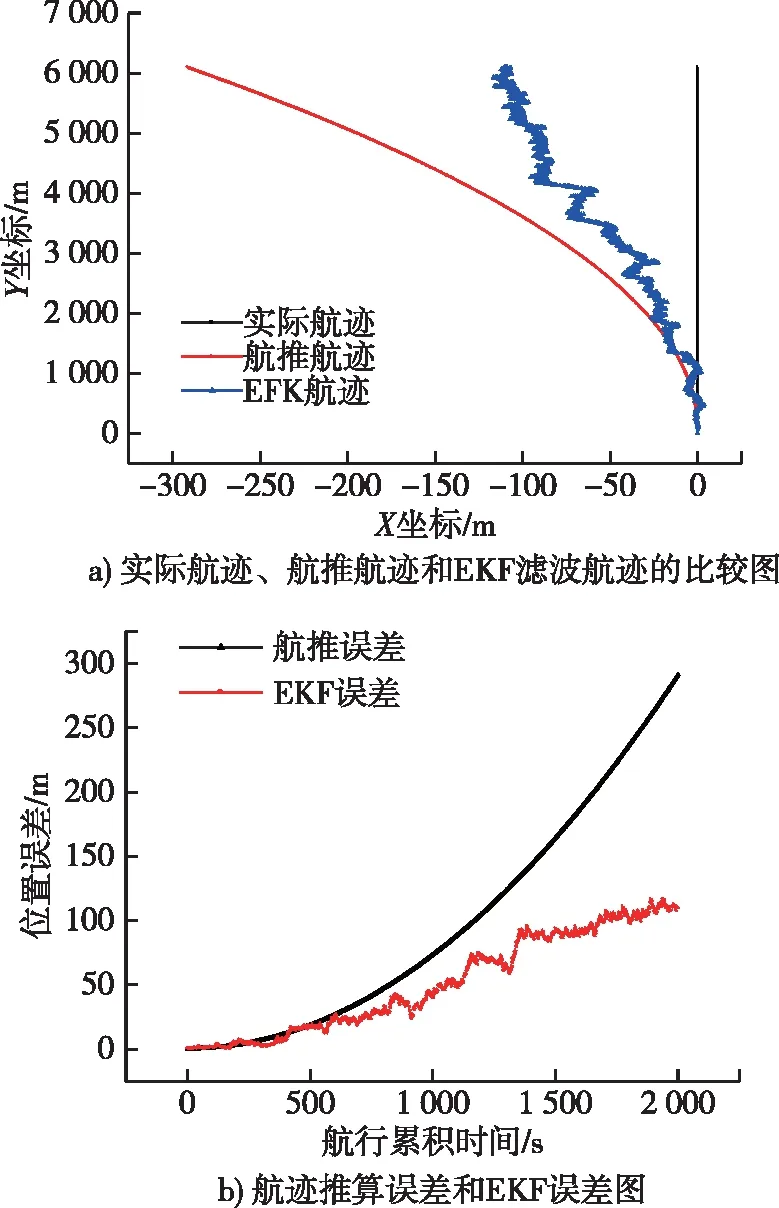
图3 从艇A的协同导航定位结果Fig.3 The result of cooperative navigation for follower A

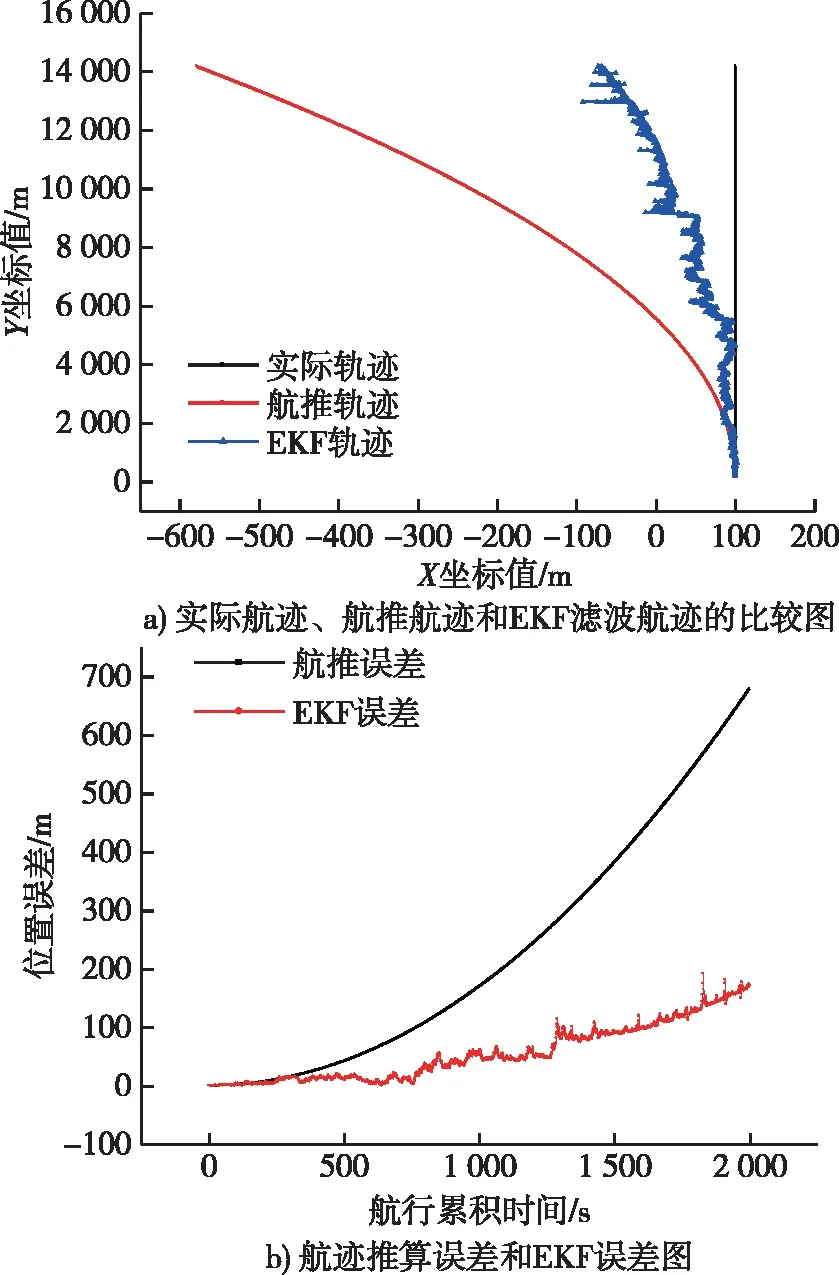
图4 从艇B的协同导航定位结果Fig.4 The result of cooperative navigation for follower B

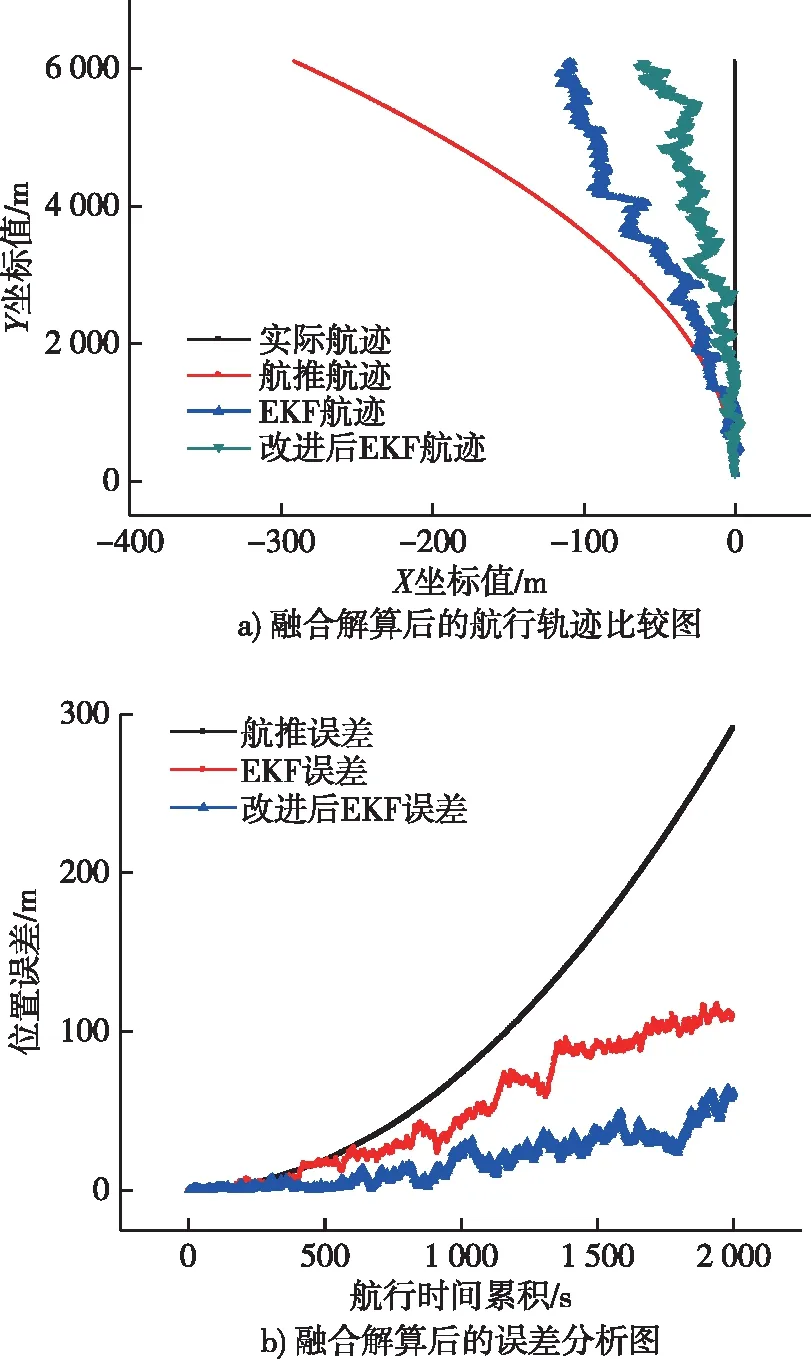
图5 改进后从艇A的协同导航定位结果Fig.5 The result of improved cooperative navigation for follower A

图6 融合解算后,从艇B的协同导航定位结果Fig.6 The result of improved cooperative navigation for follower B

图5a)和图6a)中,黑线分别表示从艇A、B实际的航行轨迹;红线分别表示航推轨迹;蓝线表示传统的协同导航轨迹;绿线表示改进后的主从式协同导航解算的轨迹。图5b)和图6b)中,黑线表示从艇A、B的航推误差;红线表示传统的主从式协同导航算法解算误差;蓝线表示改进后的主从式协同导航算法解算的误差。对比可以发现,主从式协同导航过程中,融合解算了从艇之间的测距信息,相比较传统的主从式协同导航方法,从艇A、B位置误差的发散速度得到了有效抑制,如表2所示。

3 结束语

本文针对无人艇编队的协同导航问题,基于传统的主从式协同导航算法,提出了一种增加从艇间距离观测信息的改进算法,并通过了仿真试验验证。由仿真结果可知,在一艘主艇两艘从艇的情况下,将从艇间的测距信息作为量测值进行融合解算比传统单主艇与单从艇的协同导航定位结果对误差的抑制更有效。

表2 传统算法与改进后算法的误差对比表