鸭式导弹自动驾驶仪开环截止频率的设计约束
王鹏举,杨育荣
(中国空空导弹研究院,河南 洛阳 471009)
鸭式布局是制导兵器常用的一种气动布局形式,具有操纵效率高,响应快等特点,且舵机安装在头部,避免了尾舵连接电缆的弹外气动整流问题,是战术导弹采用的一种重要体制[1-3]。相比正常式布局,鸭式布局导弹主要存在舵效系数极性相反,无最小相位零点的差异,因此,三回路过载驾驶仪结构同样适用。伪攻角反馈驾驶仪是三回路过载驾驶仪的一种典型结构,可以消除经典三回路驾驶仪的静差,同时保持较好的时域、频域响应特性及鲁棒性能,因此在战术导弹上得到广泛的应用,较多的学者和工程人员对其进行深入研究[4-9]。其中,郑鹍鹏等以一阶时间常数极小化条件提出了极点配置共圆准则,给出了控制增益与闭环极点、开环截止频率的解析关系式,方便了工程应用。但在实际应用中,对开环截止频率的选取准则研究较少,或存在约束准则过于保守以及负增益等问题,这限制了工程应用自动化程度。
本文基于鸭式布局导弹自动驾驶仪设计经验,讨论分析开环截止频率选取准则,修正了舵偏角速率约束准则,给出了更适宜工程应用的开环截止频率的约束形式。
1 极点共圆配置方法
本文讨论纵向通道的伪攻角反馈驾驶仪设计,忽略舵机、滤波器、传感器等高频部件,其结构框图如图1所示。

图1 伪攻角反馈驾驶仪框图Fig.1 Structure diagram of autopilot with pseudo angle of attack feedback
给出弹体本体传递函数为[10]
(1)
其中,a1~a5为动力学系数,A4=(a3a4-a2a5)/a3由被控对象参数决定,可以消除伪攻角反馈回路中的零点,使系统阶次降为三阶。
1.1 阻尼回路
由图1可得到阻尼内回路的闭环传递函数为
(2)
其中,
(3)
对于鸭式导弹,可设计阻尼回路开环截止频率ϖ=-Iya3>0,因此,对于静稳定弹体,阻尼回路总是稳定的,且开环频率上限受舵机等高频部件带宽约束。
系统的阻尼系数由
(4)
变成:

(5)
根据工程经验,一般Iy、a4较小,a2较大,上式可变为

(6)
因此,系统阻尼得到大幅提升,这也正是阻尼回路的目的。
1.2 增稳回路
增稳回路可视为姿态驾驶仪,保持导弹攻角稳定,等效结构框图如图2所示。
其中,取A4≈ωα可对消系统零点,增稳回路的闭环传递函数:
(7)

图2 攻角回路结构框图Fig.2 Structure diagram with angle of attack loop
系统稳定的条件为
(8)
当约束增益K0为正时,对于静稳定弹体总有系统稳定,但当a2<-a4ϖ时,则需要K0来稳定弹体。此时系统阻尼为

(9)
1.3 过载回路
图1中,从控制量处断开的开环传递函数:
(10)
将式(1)及A4代入式(10),得到
(11)
令开环传递函数幅值为1,可得系统的开环截止频率:
ωcr≈IyK4va5-Iya3
(12)
式(12)得以成立的条件包括:
(13)
结合工程经验,式(13)第二项约束明显,其表明系统的开环截止频率应远大于弹体本体特征频率。提高开环截止频率可提升系统的快速性,因此,控制系统设计应在可接受的范围内寻求开环截止频率的上界。
结合式(10)可得到系统的闭环传递函数为
ay/ayc=IyK4v(a5s2+a5a1s+a2a5-a3a4)/
(14)

det=s3+(A+2ωξ)s2+(2Aωξ+ω2)s+Aω2
(15)
对比式(14)、(15),结合式(12),可求解出控制增益:
(16)
1.4 极点共圆原则
从三阶系统等效时间的快速性,可给出闭环极点与开环截止频率的约束。三阶系统的等效时间常数近似为[11]
(17)
当实极点与共轭极点实部满足式(18)关系,系统的时间常数τ最小,即认为系统具有较好的快速性。
(18)
此时,闭环三个极点同处于半径为A的圆上,即极点共圆[5],如图3所示。

图3 时间常数极小化条件下的极点分布Fig.3 Polels distribution of extremely time constant
综上,当取定阻尼比ξ和开环截止频率ωcr,即可求解控制增益。通常取ξ=0.707,则系统的性能主要由开环截止频率决定。
2 开环截止频率的设计约束
综合考虑舵机带宽、最大舵偏角速率、零极点关系约束、增益极性等因素,提出对开环截止频率的约束准则。
2.1 舵机带宽约束
系统开环截止频率的选择受舵机等高频部件带宽的制约,为保证系统稳定,工程上一般将控制系统开环截止频率取舵机带宽的1/5~1/3[6],以保证舵机在频率ωcr处引起的相位滞后不宜过大(一般应小于30°)。
2.2 舵偏角速率约束
期望舵机工作时,舵偏角速率非饱和,即工作在线性区,由加速度指令到控制量的传递函数:
(19)
考虑阶跃加速度输入,由初值定理得到零时刻舵偏角速率初始值:
(20)
(21)
对于闭环极点共圆分布的情况,代入式(18)得:
(22)
其中,ayc为最大加速度指令,即导弹可达的最大过载。
以上约束是在假定过载指令最大值时得到的,实际经验表明,在大多数飞行条件下(包括低空)都会受到这一约束的影响。
导弹飞行过程中不可能在所有工况下都要求实现最大过载,同时,舵偏角速率也只在过载初始较短时刻需求最大,而在过载响应整个过程中占比较小,因此,式(14)约束过于保守,从而牺牲了系统快速性。基于工程经验,提出如下修正:
λ=0.3~0.5
(23)
2.3 零点约束
对于鸭式布局导弹来说,由于其不会产生非最小相位零点,不会出现系统负调现象。但零极点配置不恰当,仍会导致系统响应出现较大的反冲与超调,影响过载响应品质。
由式(1)可得到加速度传函的零点:

(24)
为了获得较好的闭环响应特性,闭环极点到原点的距离应小于零点到原点的距离,从而使闭环极点更靠近虚轴。闭环极点共圆分布的这种关系体现在如下的不等式:
A 代入式(18)得到: (25) 工程应用中,在某些设计特征点因开环截止频率选择不合适,时常会出现K0为负的情况。此时,虽然整个闭环系统是稳定的,但内回路处于正反馈状态;同时,增益表中有正有负,在飞控软件增益调度时可能导致某些中间状态下控制增益为0,因此,应尽量避免增益极性的跳变问题。 对式(16)中K0,忽略a1、a5等影响,则得K0为负的条件如下 ω2+2Aξω-ωcra4-a2<0 (26) 代入式(18)得 (27) 求解不等式得到 (28) 可见,负K0是由于系统静稳定性过大情况下,开环截止频率受到上限约束造成的。因此,想要得到正K0,则开环截止频率和阻尼比应满足: (29) 综上讨论,归纳得到开环截止频率约束条件如下: (30) 即开环截止频率选取应满足如下约束: ωcr4<ωcr (31) 某特征点如表1所示,应用上述约束准则可知,开环截止频率上限受舵偏角速率约束最严苛,表2给出最大舵偏角速率约束和放宽约束(λ取0.5)下的设计结果对比,图4、图5分别给出了最大加速度响应和舵偏角速率结果。其中,舵机带宽取220 rad/s。 表1 气动力学系数Tab.1 Aerodynamic coefficients 表2 设计结果对比Tab.2 Comparison of design results 图4 最大加速度响应Fig.4 Response of maximum acceleration 由图4、图5可见,放宽舵偏角速率约束后,在初始较短时间出现舵偏角速率饱和,但系统快速性得到提升,表2设计结果表明系统仍有足够幅值和相位裕度。 取模型的动力学系数摄动范围:a1±40%,a2±30%,a3±30%,a4±10%,a5±20%,进行100次系数随机摄动仿真,结果显示,幅值裕度变化小于2 dB,相位裕度变化小于3°,表明应用该方法设计的结果具有较好的鲁棒性,模型摄动下的阶跃响应结果如图6所示。 图5 舵偏角速率Fig.5 Rate of rudder declination 图6 模型摄动下阶跃响应Fig.6 Step response under the model perturbation 某小动压特征点如表3所示,应用约束准则可知系统零点对开环截止频率的约束最为严苛。表4给出了是否考虑零点约束的设计结果对比,可知考虑零点约束后,系统的开环截止频率显著降低。图7为阶跃响应情况对比,不考虑零点约束时会过载响应抖动严重,系统品质变差。因此,在系统设计时,应考虑零点对开环截止频率上限的约束,以保证系统良好性能。 表3 气动力学系数Tab.3 Aerodynamic coefficients 表4 设计结果对比Tab.4 Comparison of design results 图7 阶跃响应Fig.7 Step response 本文基于鸭式布局导弹自动驾驶仪设计,采用极点共圆准则的极点配置设计方法,得到控制增益与开环截止频率的解析表达式,从而简化了系统设计。讨论了开环截止频率选取受到舵机特性、系统零极点关系和增益极性等约束,结合工程应用经验,明确了舵偏角速率约束的应用条件,放宽了约束的保守性,并补充零点影响和负增益问题对开环截止频率约束形式。仿真算例验证了该约束准则的有效性和工程应用价值。2.4 K0极性约束

2.5 小结
3 算例验证
3.1 算例1


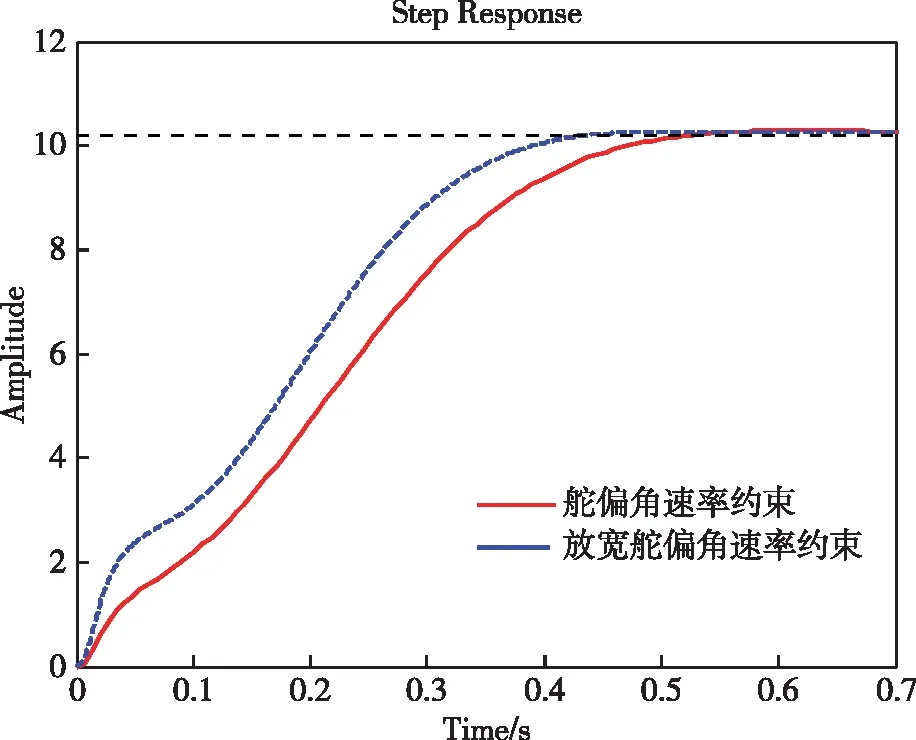
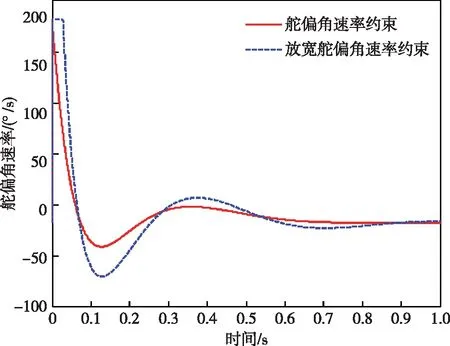

3.2 算例2



4 结束语

