基于改进遗传算法的AUV动态目标搜索算法

谢 锋,姚 尧,张晓霜

(江苏自动化研究所,江苏 连云港 222061)

自主水下机器人(Autonomous Underwater Vehicle, AUV) 航行噪声低、机动灵活、无人员伤亡等优点非常适用于各种水下作业,如探测、搜索、追踪、围堵等[1]。

目前多数AUV受续航能力限制,航速有限,面向水下有人平台搜索任务难以在任务约束时间内完成任务区域覆盖搜索[2-4]。因此如何有效规划AUV的搜索路径,使得有限时间内搜索到目标的概率最大,成为亟待解决的关键问题。AUV动态目标搜索过程实质上是连续时间和空间上的优化搜索问题,较多研究者在研究搜索作业时都进行了一定的简化处理,如将区域网格化等[5],但这种方法使得搜索过程离散化,与实际情况有着较大的差异。

遗传算法作为一种搜索启发式算法,广泛应用于解决最优化问题[6],因此其适用于上述有限时间内动态目标搜索问题,但它也存在一定的不足,如各种算子的参数选择大多依靠经验,存在着一定的随机性,算法在大规模计算问题中容易陷入“早熟”,即过早陷入局部极值,除此之外,既保留优秀个体又维持种群多样性同样也是该方法的一个难点。因此在解着决上述问题时需要对遗传算法进行优化。

1 问题描述

由于敌方目标在一定时间内航行深度较为稳定,本文重点研究二维平面内的搜索规划方法。假设某一时刻一艘AUV接收到岸基总台发送的敌目标指示信息,目标位置记为Pt0,记岸基位置为坐标原点,以正东方向为X轴,正北方向为Y轴建立平面直角坐标系,则目标位置可表示为Pt0=(xt0,yt0)。当AUV到达Pt0位置,开始执行搜索任务,记为0时刻。

AUV在前往Pt0位置过程中,水下目标也处于动态运动中,但水下目标的运动具有很强的随机性,AUV无法事先知道,故假设当AUV到达Pt0位置时,水下目标运动起始位置Pt1=(xt1,yt1)服从二维正态分布,即

(1)

其中,σ为导航误差。

在一段较长的固定时间[0,Tend]的搜索任务中, AUV和水下目标的转向时间可忽略不计。AUV为确保探测声呐的稳定性,搜索行进时采用匀速航行,期间可多次调整方向,直至搜索时间结束。相比之下,水下运动目标具有更多的不确定性,可以多次进行改向和变速操作,但水下目标在转向时由于结构和体型等原因,无法像AUV一样进行较大幅度的转向,目标在转向前的航向角αn和转向后的航向角αn+1,应满足公式(2)和(3),其中f(α1)为其开始任务时的航向角α1的概率密度函数。

(2)

(3)

目标各段速度v的取值服从 [Vmin,Vmax] 之间的均匀分布,各段航行时间t服从参数为λ的指数分布。它们的概率密度函数如下所示:

(4)

(5)

式(4)中Vmax和Vmin分别为水下动目标的最大和最小运行速度。

根据上述模型构建,所能得到的目标运动轨迹数目是无限的,无法通过列举等常规方法得出运动轨迹,但借用蒙特卡罗(Monte Carlo)方法,可以通过计算机辅助生成大量目标运动轨迹作为水下目标实际运动轨迹的模拟。蒙特卡罗目标运动模型由大量的目标轨迹组成,轨迹路线可以源自于历史数据分析,也可能源自于先验地图的仿真,也可以像前文所描述的采用随机数生成的方法,产生大量目标运动轨迹,抑或是多种数据的融合。以50束目标运动轨迹为一簇作为基础,可以将这些轨迹整合为多簇,通过计算机模拟仿真生成的一簇轨迹如图1所示。

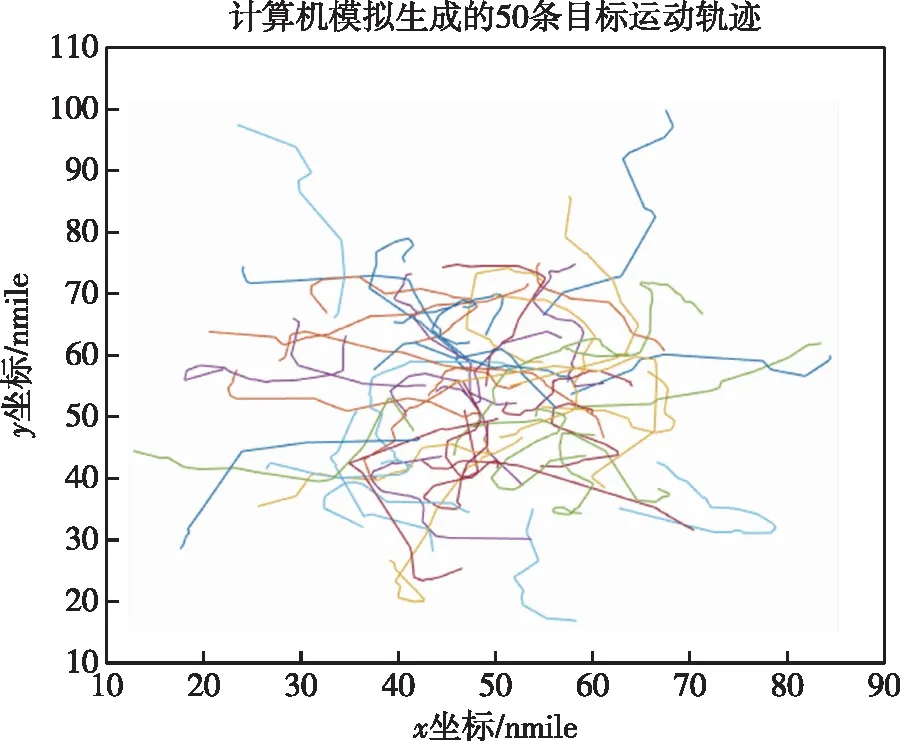
图1 计算机模拟生成的50条目标运动轨迹Fig.1 The 50 target trajectories generated by computer simulation

受水中因素的影响,AUV在搜索过程中常采用的工具是声呐,包括主动声呐和被动声呐,在本文中为扩大探索范围,可采用被动声呐进行探测,根据AUV与水下动目标的距离D(单位:海里)进行瞬时探测,瞬时探测P(D)可描述为下式

(6)

与其他搜索过程所注重的完成全覆盖搜索所用时间等完成度指标不同的是,本文将目标函数设为在一定时间内的最大探测概率,又称为累积探测概率(Cumulative Detection Probability,CDP)[7]。在0≤t≤T时,t时刻的累积探测概率(CDP)记为Fd(t),定义为[0,T]时间段内至少发生一次探测的概率,即

Fd(t)=Pr{在时刻t以前至少发生一次探测}=Pr{ 初始探测时间≤t}

2 基于改进遗传算法的目标搜索策略

遗传算法(Genetic Algorithm,简称GA)作为一种随机全局搜索优化方法,概念来源于生物系统的遗传与进化,通过模拟自然界基因层面上的复制、交叉(crossover)和变异(mutation)等现象以及自然界中的物竞天择现象,在一代又一代种群的繁衍进化中,得到最适应环境的个体,即求得问题的最优解[6]。但它也存在着易“早熟”,过早陷入极值等问题。

本文采用改进遗传算法进行搜索路径优化,并采用蒙特卡罗统计方法建立评价度指标,在种群的选择上将灾变思想与精英主义相结合,既保留优秀个体,同时也给予种群产生更优秀基因片段的机会,避免过早陷入局部极值。交叉和变异操作基于椭圆约束遗传算子,并采用混沌序列对交叉或变异点的选取进行改进,再对交叉概率与变异概率进行动态自适应,减少对经验的依赖,同时尽量在后期也维持种群的多样性,具体流程图如图2所示。

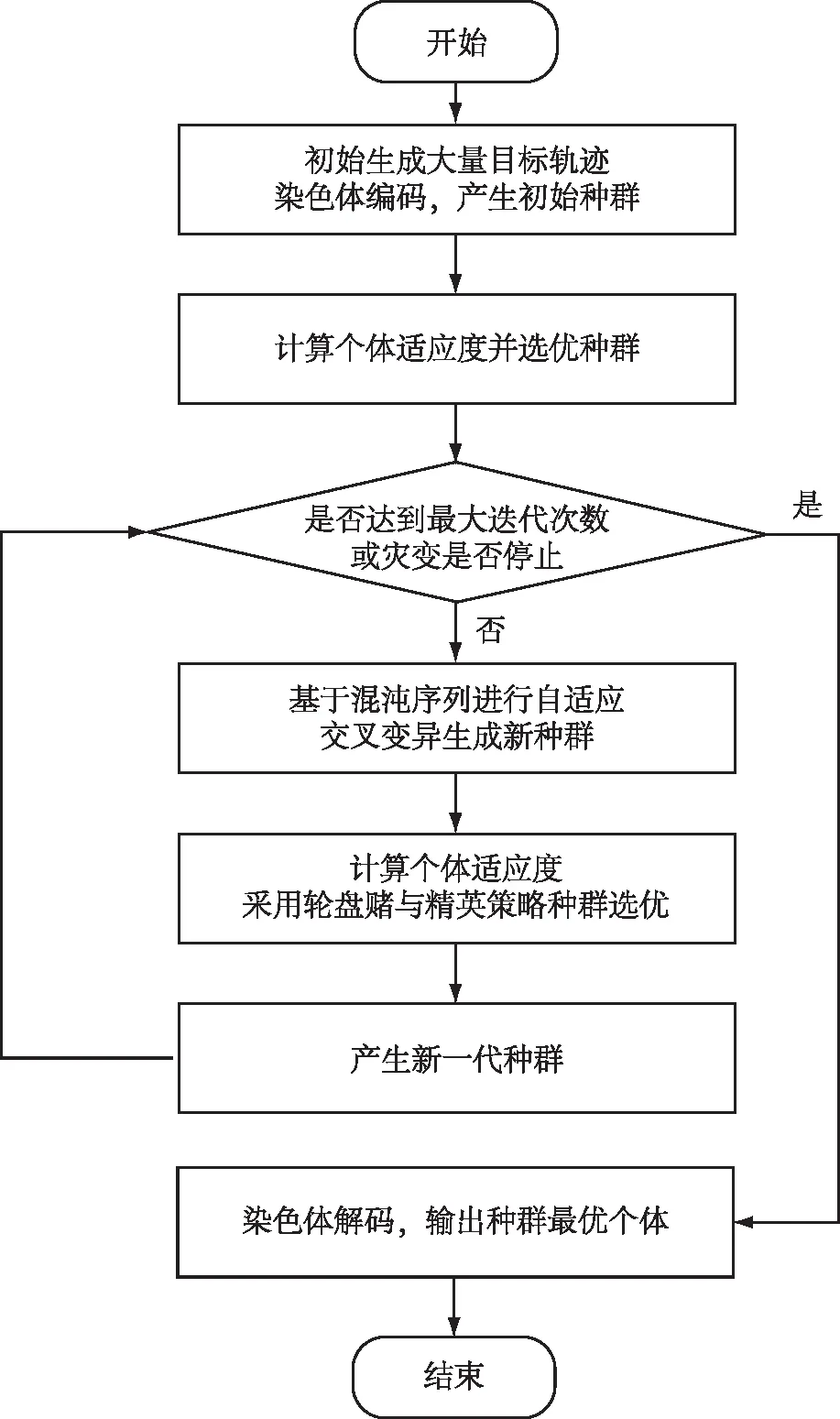
图2 改进遗传算法流程图Fig.2 Flow chart of improved genetic algorithm

遗传算法最重要的几个部分为遗传算法编码的描述,适应度函数的设计,初始种群的产生,遗传过程中选择、交叉、变异的操作和最后的迭代终止条件的设定[8]。

2.1 编码

编码作为遗传算法的首要和关键步骤,会对交叉算子、变异算子等运算方法产生重要影响,进而影响遗传算法的效率[9]。

在此问题中,AUV的搜索过程实质上是连续时间和空间上的优化搜索问题,因此AUV的编码形式采用变长实数编码。设P为种群的总体,种群大小为N,种群内的个体记为pi(i=1,2,3,…,N),表示一条搜索路径,每一个个体由多个基因组成,即pi=(gi1,gi2,…,gij,…),gij代表第i个个体上的第j个基因,而gij=(xij,yij,tij),其中xij,yij,tij分别代表第i个个体运行至节点j时的横坐标,纵坐标和时间点。

2.2 适应度函数

由于此搜索过程是连续时间和空间上的[10-12],航路实际上是无限条的,需要设计一个目标函数(适应度函数)作为评价指标,即后续选择操作的依据。

本文采用 CDP 作为适应度函数,可根据水声模型及离散探测概率公式,由蒙特卡罗法完成适应度函数的计算。假设根据蒙特卡罗法生成了S条目标路线,其中第j条路线记为Sj,而在种群某代中某一个体pi有M个基因(即M个坐标点),则其路线共有M-1段,每一段均分为10个点作为这一段的采样点,分别计算个体pi和路线Sj在这10个采样点时刻的距离差值,代入公式(6)计算得到这10个点的瞬时探测概率,取其中的最大值代表个体pi在第k段的瞬时探测概率,记为Pins(k) (k=1,2,3,…,M-1),则pi对Sj的探测概率可描述为

Pij=F(Pins(1),Pins(2),…,Pins(M-1))

(7)

根据文献[7]和实验总结,可设计得到如下CDP的计算公式

(8)

式中,α=1-e-λΔk,Δk为个体pi中第k段路线的用时,Pimax为Pins(k)中的最大值。

2.3 种群的产生

初始种群按照一定的随机性生成初始群体。按照编码规则随机生成初始群体。初始种群可采用随机生成的方式,随机生成的个体可提供更丰富的基因片段,通过交叉和选择可留下更优秀的个体。

2.4 遗传过程的选择

遗传算法中的选择操作就是用来确定如何从父代群体中按某种方法选取优秀个体,以便遗传到下一代群体。选择操作用来确定重组或交叉个体,以及被选个体将产生多少个子代个体。

现在大多数遗传算法的选择过程采用的都是轮盘赌的方式,但也会带来早期高适应度个体迅速占据种群和后期的种群中因个体适应度不大而导致的种群停止进化问题[6]。

为避免此类问题,提出灾变思想与精英主义相结合的思想。灾变思想[13]是指消灭最优秀的一部分个体,才有可能诞生更优秀的个体,而精英主义思想是指在每一次产生新一代时,保留上一代最优秀的一部分个体到下一代。看似冲突的两者却可以相结合。在每一代进行交叉运算时,直接将最优秀的个体复制到下一代,但当连续多代的最优秀个体没有变化时,则认为算法可能已经陷入了局部极值,此时进行灾变操作,将最优秀的部分个体消灭(包括直接保留的最优秀个体),再进行交叉变异等操作,在经历过若干次灾变后产生个体的适应度与灾变前一样时,则停止灾变,同时认为算法已经跳出局部极值,表明进化完成。

2.5 遗传过程的交叉

本文采用基于椭圆约束的单点交叉策略[14-15],交叉概率设为Pc。如图3所示,若选择种群内的两个个体(即两条染色体)p1和p2进行交叉操作,A、B、C三点位于染色体p1上,坐标分别为XA,XB,XC,在时间轴上所代表的时间分别为tA,tB,tC,D、E、F三点位于染色体p2上,坐标分别为XD,XE,XF,在时间轴上所代表的时间分别为tD,tE,tF,而T1和T2分别位于染色体p1和p2上,但它们在时间轴上都代表同一时刻tc,由于AUV一直保持匀速运动,染色体的交叉过程应满足椭圆约束。在此设d(Xi,Xj)代表Xi和Xj两点间的欧氏距离,而Xi可表示为Xi=(xi,yi),因此有

(9)

以图3为例,分别选取染色体p1和p2上的B、E两点作为交叉点,很明显,B、E两点需要满足

d(B,E)≤V0×|tB-tE|

(10)

其中V0为AUV的匀速速度。

但线段BE不可能每次都恰好满足AUV运动时的空间和时间上的连续性,即d(B,E)=V0×|tB-tE|不是对所有的交叉点B和E都成立, 因此,需要找一个点G,使得E、G间距离与B、G间距离之和等于E到T2的距离与T1到B的距离之和,即:

d(B,G)+d(E,G)=V0×|tT2-tE|+V0×|tT1-tB|=

V0×|tc-tE|+V0×|tc-tB|=V0×|tB-tE|

(11)

而V0×|tB-tE|对于任意两个确定的交叉点B和E,其值都为一个常数,因此可看出G点位于以B、E为焦点的椭圆上,但由于时间上的不可逆性,通过基于椭圆约束的交叉方法只能生成1条子染色体,如图3中只能生成DEGBC这条子染色体。

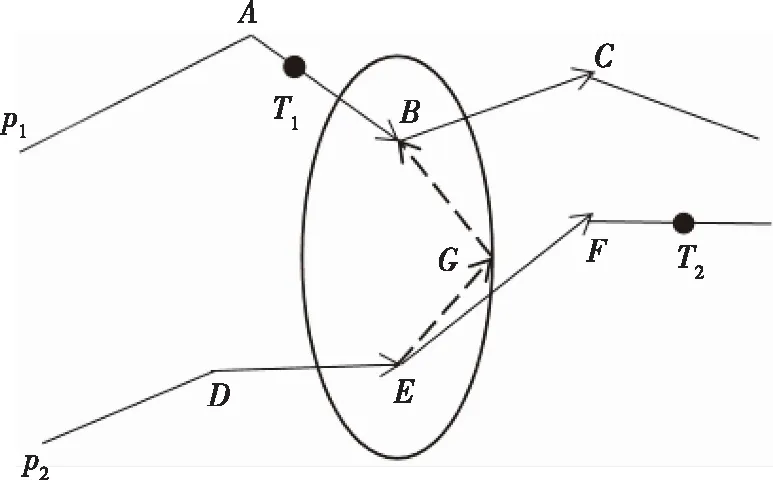
图3 基于椭圆约束的交叉节点示意图Fig.3 Schematic diagram of crossover diagram based on elliptic constraints

例子中的交叉点B、E可按照Logistic混沌序列[16]方式进行选取,具体步骤如下:若被选择染色体p1共有20个节点(包括起点和终点),编号为1-20,因此可选取的交叉节点只有2-19号。先取一个(0,1)的随机初始值,再利用混沌序列x(n+1)=4x(n)(1-x(n))迭代多次(即多次代入x(n))产生一个新值,再把这个值乘以18再加2,最后取整数部分即可。假如这个数为14,则表示这条染色体的14号节点作为交叉点。同理可选取出p2的交叉点,再按时间先后顺序生成了染色体。这种选取方式对原来的解改动较小,可以削弱遗传算法在组合优化算法中产生的寻优抖振问题,可以提高算法收敛精度[16]。

由于交叉过程中G点的选择具有较强的随机性,为做出一定的规范,取其椭圆短轴的顶点,顶点的选取应使EG的方向与DE的方向夹角不超过90°。

2.6 遗传过程的变异

变异操作是实现全局最优解的关键环节,增加变异运算可以防止过早陷入局部最优解。在此模型中,变异概率设为Pm,可采用的合适的变异操作有替换节点或消除节点两种方案,采用替换和消除操作的概率相等,都为50%。被替换节点Ni同样按照Logistic混沌序列方式进行选取。

替换节点和交叉一样,也受到椭圆约束,如图4所示。p为一条染色体,替换节点选择Ni,Ni的前一个节点为Ni-1,Ni的后一个节点为Ni+1,为保持AUV运动时在空间和时间上的连续性,将节点Ni替换为N′i时,应满足

d(Ni-1,N′i)+d(N′i,Ni+1)=d(Ni-1,Ni)+d(Ni,Ni+1)

(12)

对每一条确定的染色体p,d(Ni-1,Ni)+d(Ni,Ni+1)都为一个常数,因此,更改的节点N′i也位于以Ni-1和Ni+1为焦点的椭圆上。

消除节点操作是指删去染色体中的某一节点Nj,将Nj的前一个节点Nj-1以及Nj的后一个节点Nj+1连起来,并且将从Nj+1及以后的节点的对应时间都进行改正,并在最后的节点末尾加上一段运动轨迹,以弥补因为删除节点而缺少的时间,使AUV能在Tend时刻结束搜索。

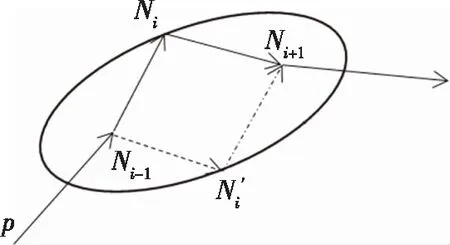
图4 基于椭圆约束的替换节点示意图Fig.4 Schematic diagram of replacement node based on elliptic constraint

2.7 自适应的交叉与变异概率

遗传算法中的交叉概率Pc和变异概率Pm对算法的行为和性能影响非常大,Pc过大会导致遗传模式出现问题,高适应度的个体很难存活,Pc过小会导致搜索速度慢,种群停滞不前。Pm过大则偏向于随机搜索,Pm过小则不易产生新的个体,且算法各时期对交叉和变异的需求都不同,因此,Pc和Pm应随着适应度自动变化。本文采用任子武[17]等提出的自适应公式。

(13)

(14)

其中,变量Pc和Pm为自适应后的交叉概率和变异概率,fmax为每代种群中最大的适应度值,favg为每代种群中平均适应度值,f′为要交叉的两个个体中较大的适应度值,f为要变异个体的适应度值。Pc1、Pc2、Pm1、Pm2都有规范的取值。

3 实验与仿真

本次实验仿真平台为Matlab,实验参数设置:水下动目标最小航速为0节,代表静止,最大航速为20节;被发现初始位置点Pt0为(50,50) ,单位为海里,其运行路线为折线;AUV行进匀速速度为10节,两者水平面间距离为2 海里,搜索任务总时长为3 h。为使结果更具有适用性和可靠性,在初始生成的路线数量设定上应尽可能多一些,因此设定初始种群的数量为100,进化最大代数为100,采用蒙特卡罗法仿真的水下动目标路线为2 000条。选择操作中直接保留优秀个体中的适应度值前2%的个体,而灾变操作中直接删除的个体占总数的5%,交叉算子和变异算子中的Pc1、Pc2、Pm1、Pm2取值采用经典取值,分别为0.9、0.6、0.1、0.001。

先采用外螺旋式传统算法进行实验,可得到其行进路线,如图5所示,并与用蒙特卡罗法生成的2 000条水下目标运动路线进行仿真计算,可得出其探测概率为0.429。

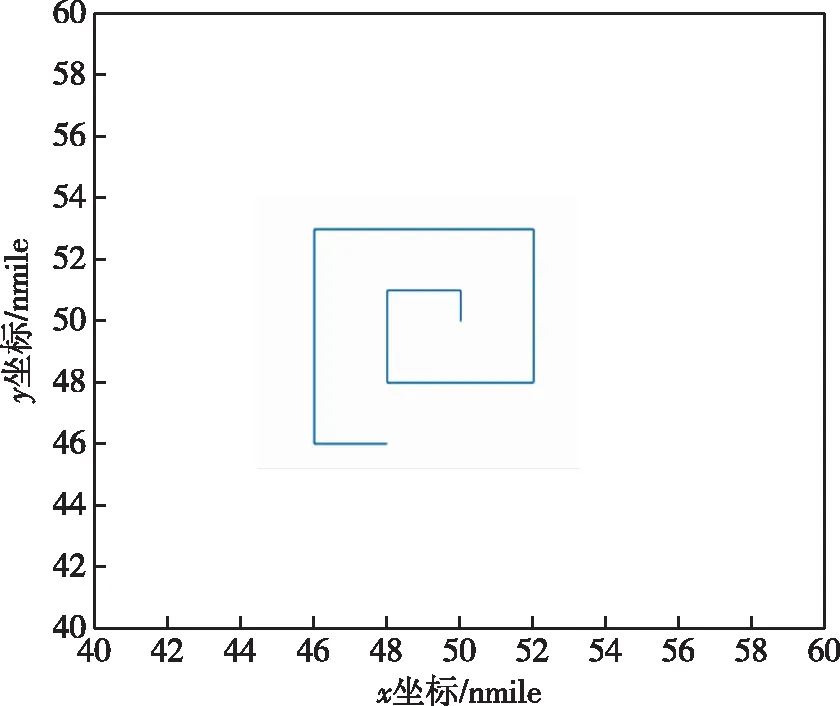
图5 外螺旋式搜索路径Fig.5 External spiral search path

传统遗传算法在同样的仿真环境,问题模型以及种群数目、目标数目和种群迭代数目等参数相同的条件下,得到的最优路径路线如图6所示,其各代最优适应度函数曲线如图7所示,各代探测概率中的最大值为56.1%。从这个最大值可以看出,经典遗传算法相比外螺旋式传统算法,路径整体也呈现外螺旋式结构,但不规则,且各代最优适应度函数曲线整体先逐渐上升后趋于稳定。因为经典遗传算法未引入精英主义策略,所以该函数曲线不是每代的最大探测概率都能保证比上一代大,即呈现波动上升的趋势,且遗传算法由于自身的局限性,非常容易陷入局部极值,像该曲线一样,从44代开始最大探测概率就在53%上下波动。

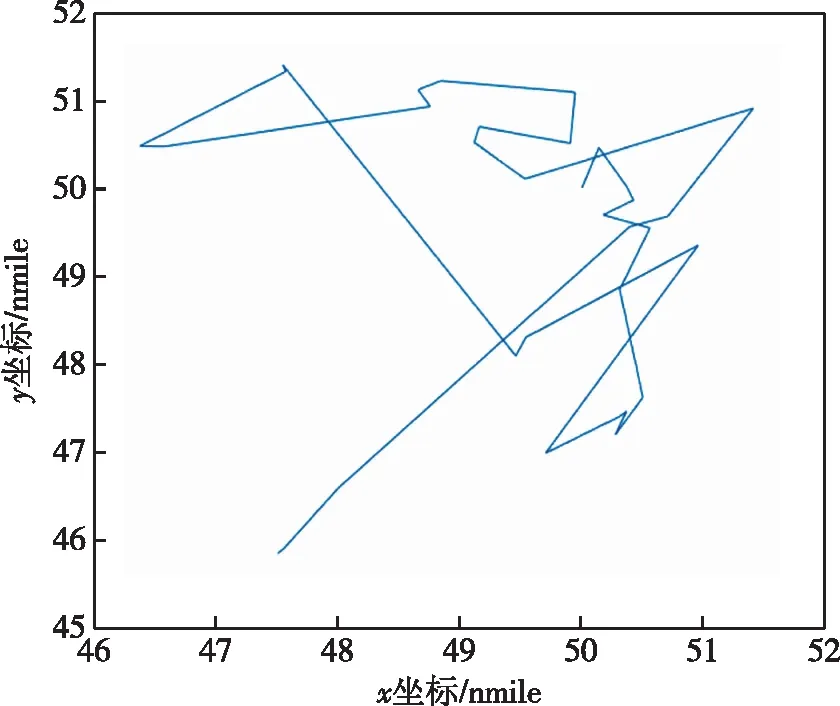
图6 经典遗传算法最大适应度个体搜索路径Fig.6 Classical genetic algorithm maximum fitness individual search path

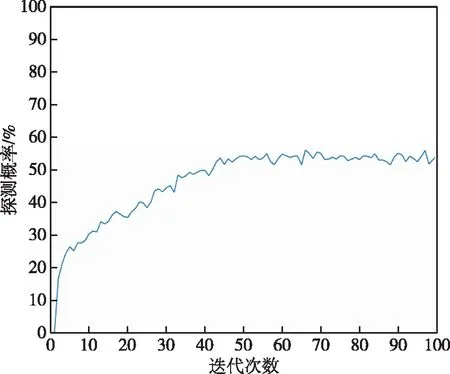
图7 经典遗传算法最大探测概率进化曲线Fig.7 Evolution curve of maximum detection probability of classical genetic algorithm

由改进遗传算法得到的最优路径路线如图8所示,此路线和传统遗传算法一样,呈不规则的外螺旋状。改进遗传算法各代最优适应度函数曲线如图9所示,各代探测概率中的最大值为63.3%,从此值的对比可看出改进遗传算法累积探测概率明显优于外螺旋式传统算法,也优于经典遗传算法。由于引进了精英主义思想,保留最优秀个体,除了灾变发生时曲线基本不会下降。当多次最优适应度基本不变时,会进行灾变操作,去除最优的部分个体,此时曲线会降低,后逐步上升。改进遗传算法和经典遗传算法由于计算量基本相同,所用时间都较长,经典遗传算法收敛速度更快,但它更容易陷入极值,改进遗传算法在搜索概率上更具优势。

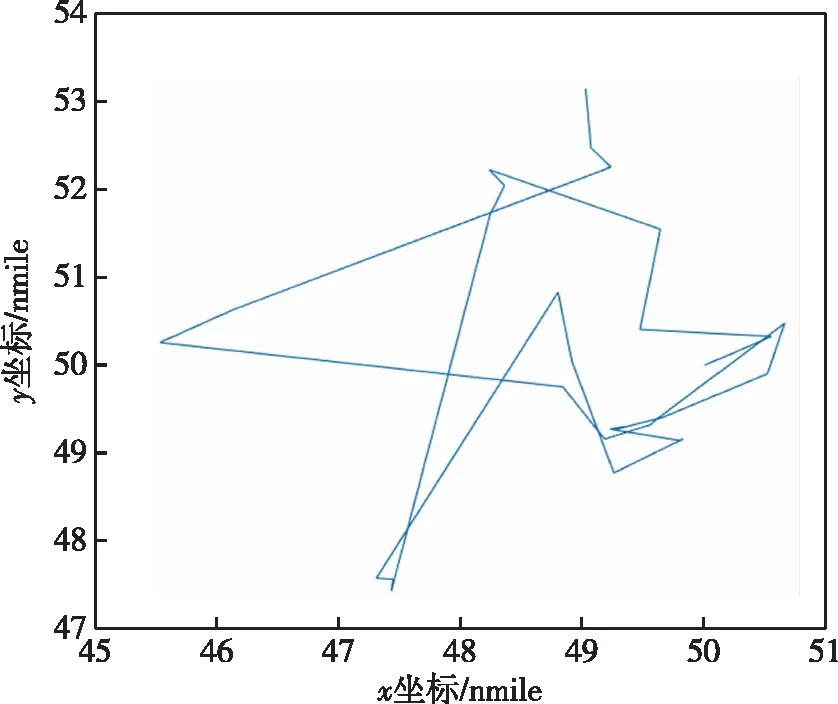
图8 改进遗传算法最大适应度个体搜索路径Fig.8 Improved genetic algorithm for maximum fitness individual search path

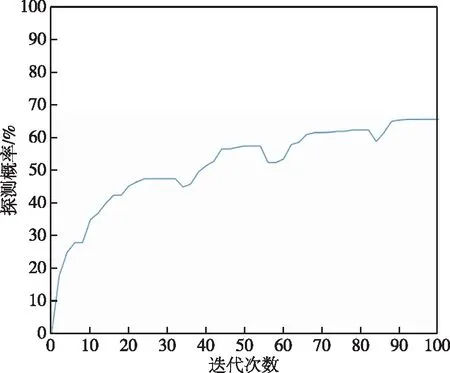
图9 改进遗传算法最大探测概率进化曲线Fig.9 Evolution curve of maximum detection probability of improved genetic algorithm

4 结束语

针对未知区域的动态目标搜索问题,本文提出采用灾变思想与精英主义相结合的改进遗传算法,采用蒙特卡罗统计方法生成大量目标运动轨迹,作为计算种群个体适应度依据。同时在适应度函数的设计上结合水声模型提出一种新型的累积探测概率算法,使其具有更明显的区分性。种群选择方法上将灾变思想与精英主义相结合,在保留优秀个体的同时也给予种群产生更优秀基因片段的机会,有效跳出局部极值。交叉和变异操作基于椭圆约束遗传算子,并采用混沌序列对交叉或变异点的选取进行改进,提高随机性带来的差距,加速跳出局部极值。交叉概率与变异概率采用动态自适应策略,减少对经验的依赖,并在后期维持种群的多样性。本算法相较于外螺旋式传统算法和经典遗传算法,能有效跳出局部极值,提高搜索到动态目标的概率。

尽管此方法得到了较高的搜索概率,但适用场景有限,接下来会考虑AUV与目标的纵向运动,将此方法扩展到三维仿真环境中,同时根据实际环境增加障碍物,进一步优化算法的适应度函数设计,提高算法泛用性与可靠性。