基于移动目标法兰的LNG卸料臂自动对接控制算法研究

刘司杰,徐大林,刘志成

(连云港杰瑞自动化有限公司,江苏 连云港 222006)

近年来,液化天然气(Liquefied Natural Gas,简称LNG)作为清洁能源日益受到国内外青睐,其大气污染物排放量和温室气体排放量相对煤和石油都少得多[1]。我国也无法摆脱对天然气的需求,需要大量建设LNG接收站,而LNG装卸系统(以下简称“装卸系统”)是安装在接收站的重要设备,LNG卸料臂(以下简称“卸料臂”)和液压系统是装卸系统的重要组成部分,其安装于LNG专用码头,分为液相臂和气相臂,分别通过与LNG船上的法兰相连来实现卸料[2]。

目前,以德国SVT、法国FMC和日本NIIGATA所领衔的国外主流生产厂商所生产的卸料臂鲜有具备自动对接功能[3-4],从而造成了在对接过程中需要操作员拿着操作手柄进行复杂的操作,并且海面往往不是绝对的风平浪静,由于海面的波浪,造成船的微小晃动,船上的法兰也将会有微小的移动。在这种情况下,操作员在操作手柄的同时,还需要根据法兰的移动实时进行调整,操作复杂度进一步加大,不仅导致了效率低下,而且极易因为操作员的误操作而导致重大安全事故。在全球首台拥有自动对接功能的卸料臂在天津成功完成自动对接这一坚实基础上,研究移动目标法兰在小扰动情况下实现实时跟踪,可以极大简化操作员的对接操作复杂度,提高对接效率,意义重大。

卸料臂的自动对接控制主要体现在对旋转关节这一机械结构的控制(以下简称“关节控制”)上,其目的是尽可能使当前实际角度与当前期望角度相等,是基础也是重要的一环。在自动控制方面,通常有三个评价指标,分别是调节时间、超调量和稳态误差[5]。调节时间是指在阶跃信号作用下,系统由初始状态到进入稳态所经历的时间,一般用来衡量系统的响应快慢;超调量是指在阶跃信号作用下,系统最大值超过稳态值的百分比,一般用来衡量系统的稳定性;稳态误差是指系统达到稳态后离目标值的偏差,一般用来衡量系统的准确性。在关节控制中,若调节时间过长,则会因为响应过于滞后而导致跟踪失败,若超调量过大,则会导致末端运动变化过于剧烈而偏离既定的路线,严重的会造成安全事故,若稳态误差过大,则会使得与期望位置产生偏差,无法实现对接。本文在现有算法能够实现稳态误差为零的基础上,将缩短调节时间和减小超调量作为关节控制优化的目标。文献[6]在对卸料臂和液压系统分别建立其各自的动力学模型的基础上,采用PD控制算法,在仿真中达到了调节时间、超调量和稳态误差较小的良好性能。然而,实际的卸料臂大多由绳轮带动的液压伺服控制,由于液压系统以及卸料臂本身的绳子收缩所带来的时延等诸多因素的影响,卸料臂是一个非线性、时变系统[7],采用诸如PD控制等线性控制算法已经无法适应控制需求,本文在上述研究基础上,基于模糊控制理论进行关节控制算法研究。

1 关节控制算法研究

卸料臂的驱动关节由四个组成,分别是回转、内臂、外臂和三维接头,其驱动系统为电液比例速度驱动系统,通过比例阀的流量大小的调节进而实现关节运动速度调节,而比例阀流量大小与电磁阀的有效开度成正相关,因此,通过控制电磁阀的开度则间接实现关节运动速度的控制[8]。

1.1 PID控制算法

PID控制算法结构简单,并且具有一定的可靠性,原理图如图1所示。

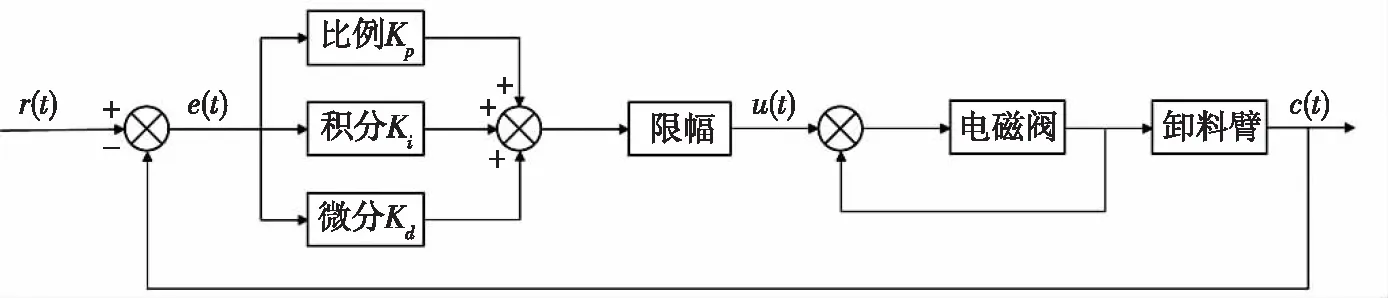
图1 PID控制算法原理图Fig.1 Principle of PID control algorithm

PID控制算法是针对期望角度与实际角度的偏差e(t)进行比例、积分、微分运算,再通过软限幅的限定输出电磁阀有效开度u(t),进而对卸料臂运动速度进行控制。

通过调节比例、积分、微分参数Kp、Ki、Kd实现控制,其中比例参数Kp对系统的控制精度和响应速度产生影响,若Kp过小,将会降低系统的控制精度和响应速度,在卸料臂自动对接过程中将会影响其跟踪性能和稳态误差,若Kp过大将容易使得系统震荡而失稳;积分参数Ki则起到消除系统稳态误差的作用,过小将会降低系统的控制精度,过大则会引起超调甚至震荡;微分参数Kd用于提升系统响应的灵敏性。

PID控制算法作为一个结构简单的线性算法,在卸料臂这种非线性较强的系统的控制上表现并不出色,其仅仅在超调量和稳态误差上实现了控制,而系统的响应速度较慢,无法适应目标法兰移动时的实时跟踪的需求,并且PID控制算法的参数受环境温度的巨大影响,每当环境温度发生巨大变化时,参数需要人工进行适应性调节,而参数的调节受到人员经验、外界干扰等影响,不可控且低重复性。

针对以上问题,将非线性算法引入卸料臂关节的控制中,本文采用基于模糊控制理论进行控制,一种是模仿人的操作行为,将其直接作用于电磁阀上,即模糊经验控制算法,另一种是与PID控制相结合,先模糊控制理论作用于PID参数上,再由PID控制算法作用于电磁阀上,即模糊PID控制算法。

1.2 模糊经验控制算法

卸料臂关节控制的模糊经验控制算法是运用模糊控制理论,构建模糊控制规则表并存入规则库中,根据卸料臂的实际偏差e(t)和偏差变化率de(t)/dt以及规则库里的相关规则依次进行模糊化、模糊推理和解模糊,最终将有效开度u(t)作用在电磁阀上,而模糊控制规则表是基于操作员手动操作卸料臂实际进行对接控制时的经验总结,因此模糊经验控制算法是一种仿人的智能控制算法[9],其具有很高的可靠性和环境适应能力。原理图如图2所示。

1)模糊化

模糊化完成将实际输入通过模糊集合形式表达的过程。卸料臂关节控制的模糊经验控制算法的输入为实际偏差e(t)和偏差变化率de(t)/dt,输出为电磁阀有效开度u(t),模糊集合划分为A={负大NB,负中NM,负小NS,零ZE,正小PS,正中PM,正大PB}。

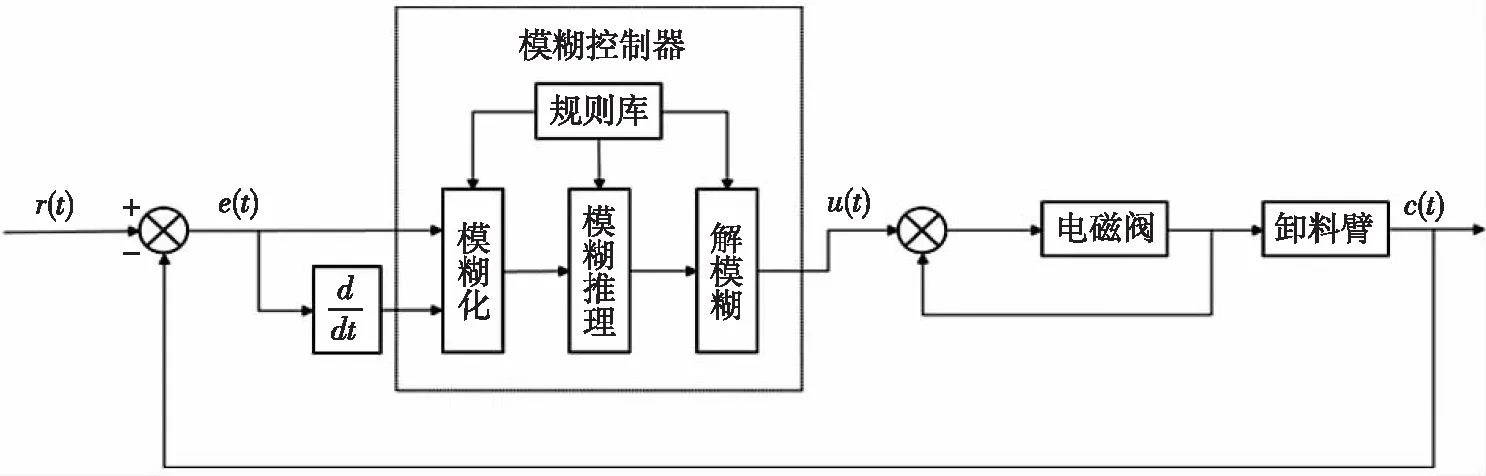
图2 模糊经验控制算法原理图Fig.2 Principle of fuzzy control algorithm

一般来说,当实际偏差e(t)较大,即实际角度离目标角度相距很远时,在控制上采用较大的液压阀开度使实际角度迅速追赶上目标角度即可,而当实际偏差e(t)处于较小偏差时,即实际角度接近于目标角度时,需要进行精度较高,稳定性较好的智能化控制,模糊控制理论恰好就是利用这个控制思想,在论域外输出较大的液压阀开度,而在论域内进行非线性精细化控制,而模糊经验控制算法针对实际偏差e(t)处于较小偏差时进行精细化控制,因此其论域的选取不宜过大,结合实际对卸料臂关节的调试情况,最终选取实际偏差e(t)的论域为[-2,2](单位:°)。由于卸料臂结构以及装配件要求,以及自动对接时保证安全的需要,每秒1度的关节运动速度已经达到较快的速度范围,选取偏差变化率de(t)/dt的论域为[-1,1](单位:°/s)。电磁阀有效开度u(t)的论域以及e(t)、de(t)/dt的隶属度函数设置为可调节,依据各个关节的运动特性通过实验来确定。

2)模糊推理

在模糊推理前,需要形成模糊控制规则表,它的形成依靠操作经验总结,或者依据人的直觉进行调整,这凸显了其“仿人”的智能特性。当实际偏差e(t)远小于0,即期望角度远小于实际角度时,说明此时实际角度朝负向走得过慢而无法跟上期望角度,或者实际角度朝正向走得过快而超越了期望角度,电磁阀有效开度u(t)应取负向较大值而驱动实际角度迅速往负向运动,或者迅速减速,而当e(t)接近于0时,则要视偏差变化率de(t)/dt而定,当de(t)/dt远小于0时,说明e(t)虽然不大但有很强的往负向变化的趋势,故此时电磁阀有效开度u(t)也应取负向较大值来抵消这一趋势,当de(t)/dt接近于0时,说明e(t)不大并且其往负向或正向的趋势不强烈,故此时仅需要给电磁阀有效开度u(t)一个较小的值即可,而当de(t)/dt远大于0时,说明e(t)虽然为负向不大的值但有很强的往正向变化的趋势,此时仅仅需要给电磁阀有效开度u(t)一个较小的值,甚至给零,利用其惯性即可,根据对称性,同理可以推理当实际偏差e(t)为正向的各种情况。根据操作经验及调试情况,模糊控制规则表的整定结果如表1所示。

将模糊控制规则表转换为模糊语句“If (eis XX) and (de/dtis YY) then (uis ZZ)”,并将其输入Matlab中进行模糊推理,求出基于电磁阀有效开度u所对应模糊集合A的隶属度。模糊经验控制器的结构图如图3所示。

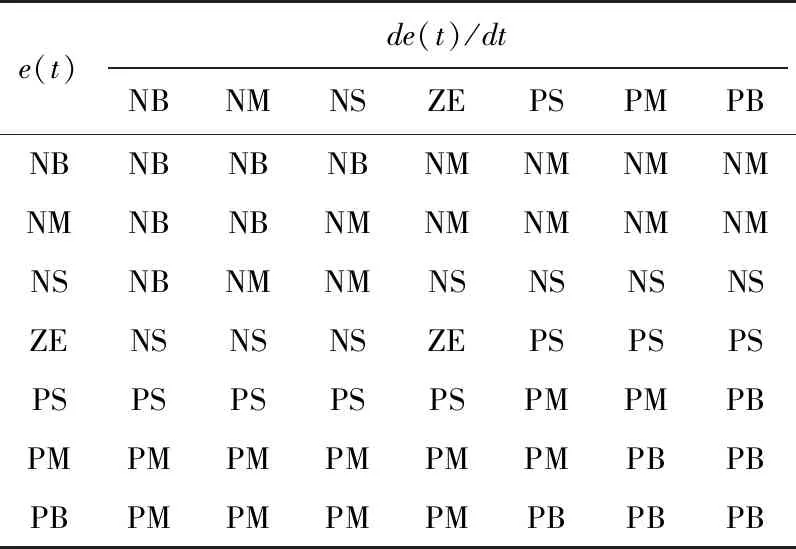
表1 u(t)模糊控制规则表

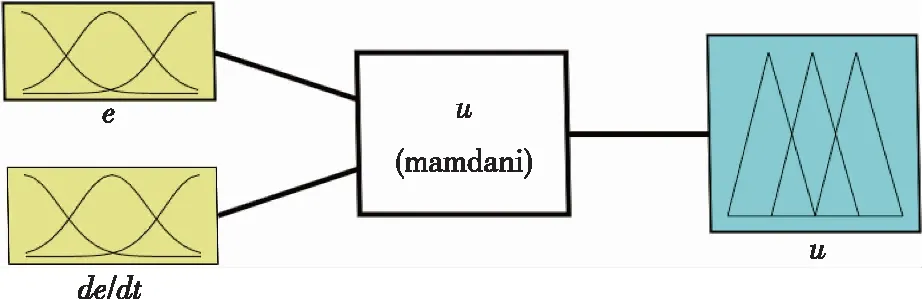
图3 模糊经验控制器结构图Fig.3 Structure of fuzzy control algorithm based on experience

3)解模糊

解模糊采用的方式为重心法[10],离散化后计算公式如式(1)所示。

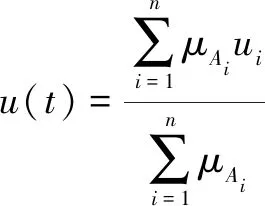
(1)

其中,Ai∈A,μAi为Ai的隶属度,ui为对应Ai的值。解模糊后的输出结果如图4所示。

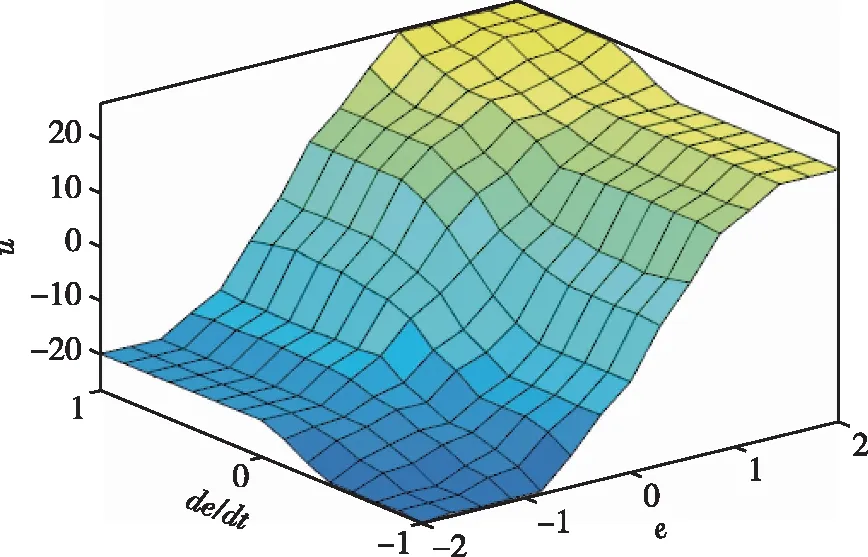
图4 u(t)与e(t)、de(t)/dt模糊关系Fig.4 Fuzzy relation between u(t) and e(t)、de(t)/dt

1.3 模糊PID控制算法

关节控制的模糊PID控制算法是将模糊控制与PID控制相结合,将卸料臂的实际偏差e(t)和偏差变化率de(t)/dt先输入模糊控制器中,经过模糊化、模糊推理和解模糊求得PID参数调整值ΔKp、ΔKi、ΔKd,然后根据调整后的PID参数计算电磁阀有效开度u(t),从而完成整个控制过程,故模糊PID控制算法有对PID参数进行实时调整的功能。原理图如图5所示。

1)模糊化

卸料臂关节控制的模糊PID控制算法的输入为实际偏差e(t)和偏差变化率de(t)/dt,输出为PID参数调整值ΔKp、ΔKi、ΔKd,模糊集合划分为A={NB,NM,NS,ZE,PS,PM,PB}。

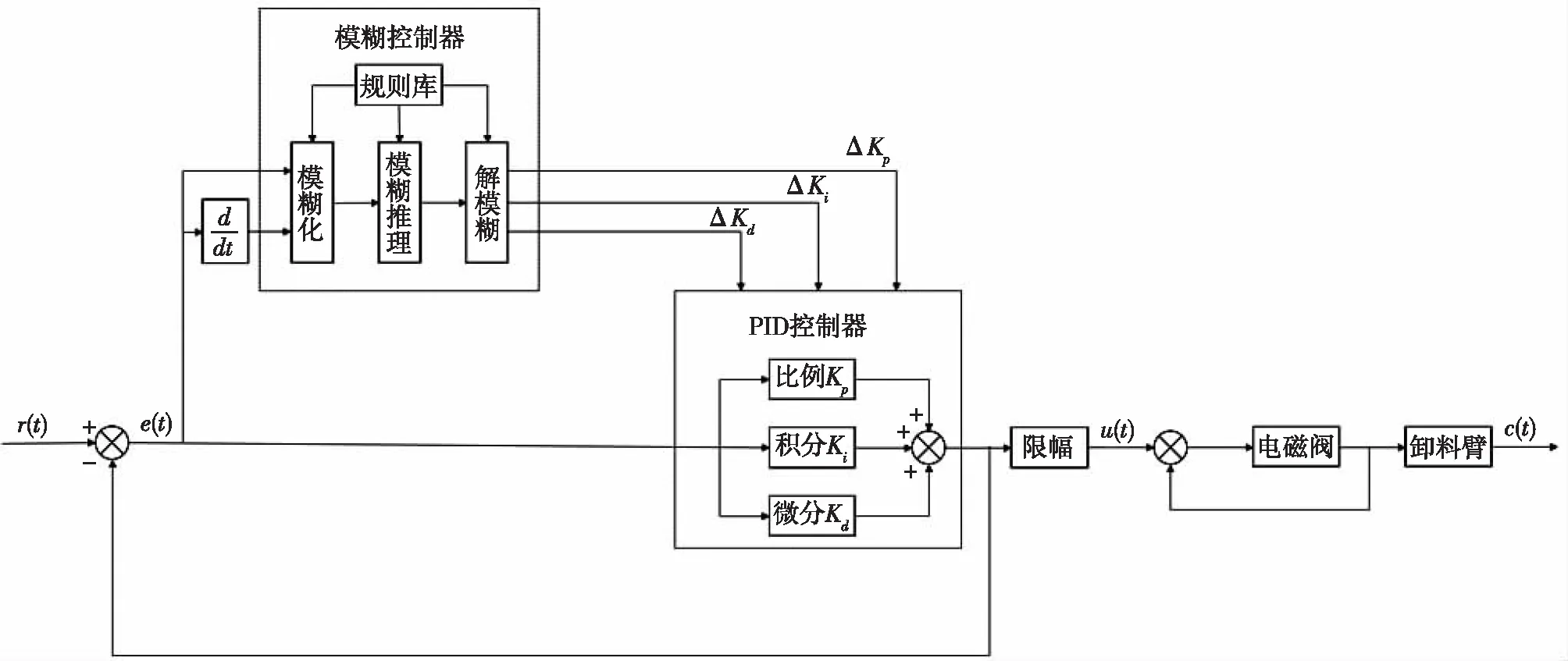
图5 模糊PID控制算法原理图Fig.5 Principle of fuzzy PID control algorithm

模糊PID控制算法也是针对实际偏差e(t)处于较小偏差时进行精细化控制,因此其论域的选取不宜过大,结合实际对卸料臂关节的调试情况,最终选取实际偏差e(t)和偏差变化率de(t)/dt的论域分别为[-2,2](单位:°)和[-1,1](单位:°/s),PID参数调整值ΔKp、ΔKi、ΔKd的论域以及e(t)和de(t)/dt的隶属度函数设置为可调节,依据各个关节的运动特性通过实验来确定。

2)模糊推理

对于模糊PID控制算法而言,模糊控制规则是作用在PID参数调整值ΔKp、ΔKi、ΔKd上的,故须对三个参数的调整参量分别设计模糊控制规则,设计原则:实际偏差e(t)偏大时,需适度减小偏差,此时应取较大的ΔKp、ΔKi与较小的ΔKd;当实际偏差e(t)处于中等大小时,此时在适度减小偏差的同时须避免超调,故须缩小ΔKi;实际偏差e(t)较小时,以“保稳”为主,增大ΔKp、ΔKi,减小ΔKd。根据上述大致的规则以及实际调试,设计模糊控制规则表如表2-表4所示。

将模糊控制规则表转换为模糊语句“If (eis XX) and (de/dtis YY) then (… is ZZ)”,并将其输入Matlab中进行模糊推理,求出基于ΔKp、ΔKi、ΔKd所对应模糊集合A的隶属度。

3)解模糊

解模糊过程与模糊控制一样,依旧采用重心法[10],解模糊后ΔKp、ΔKi、ΔKd的输出结果如图6-图8所示。

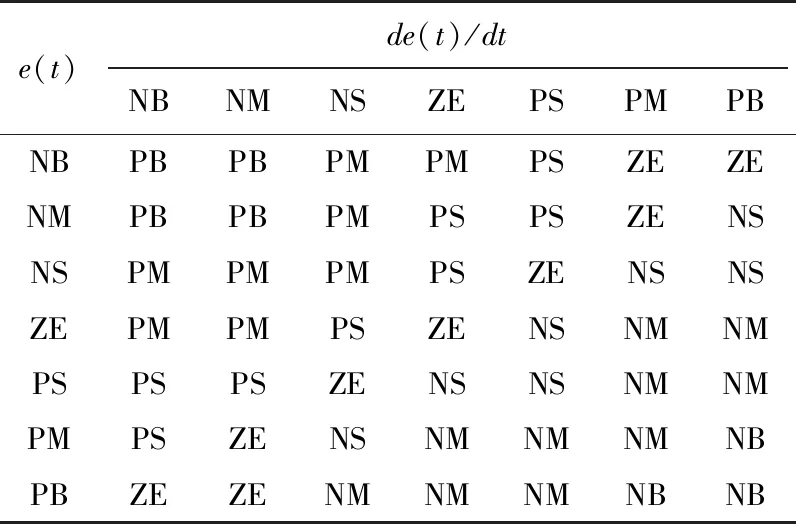
表2 ΔKp模糊控制规则表

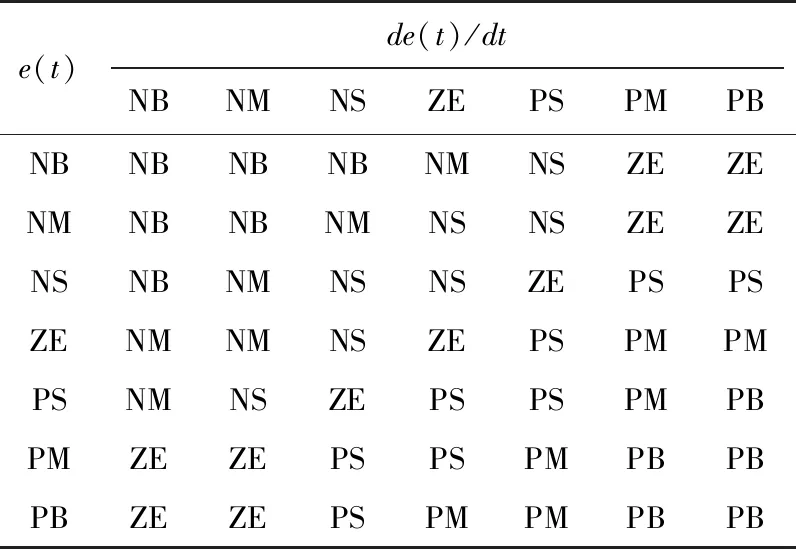
表3 ΔKi模糊控制规则表

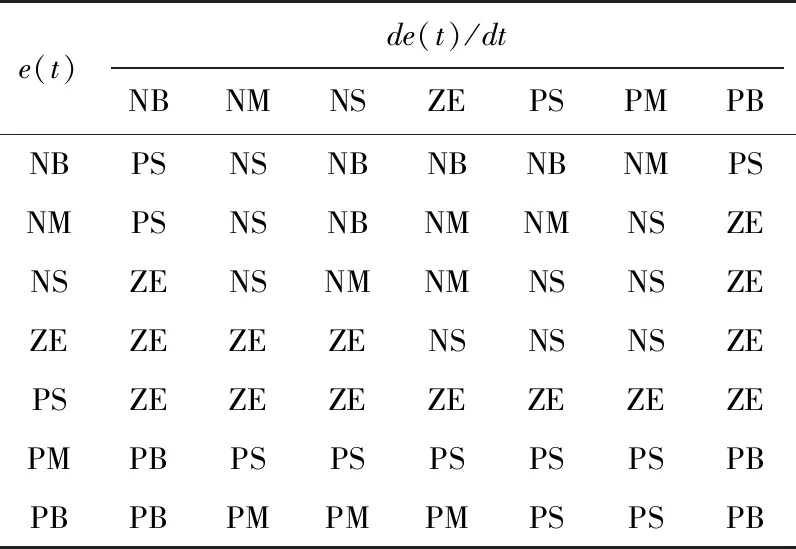
表4 ΔKd模糊控制规则表

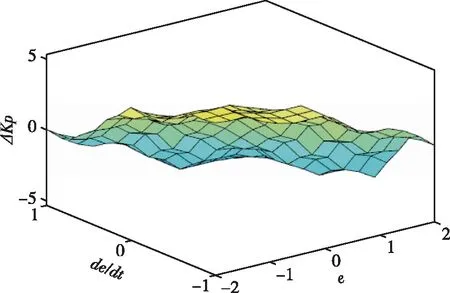
图6 ΔKp与e(t)、de(t)/dt模糊关系Fig.6 Fuzzy relation between ΔKp and e(t)、de(t)/dt

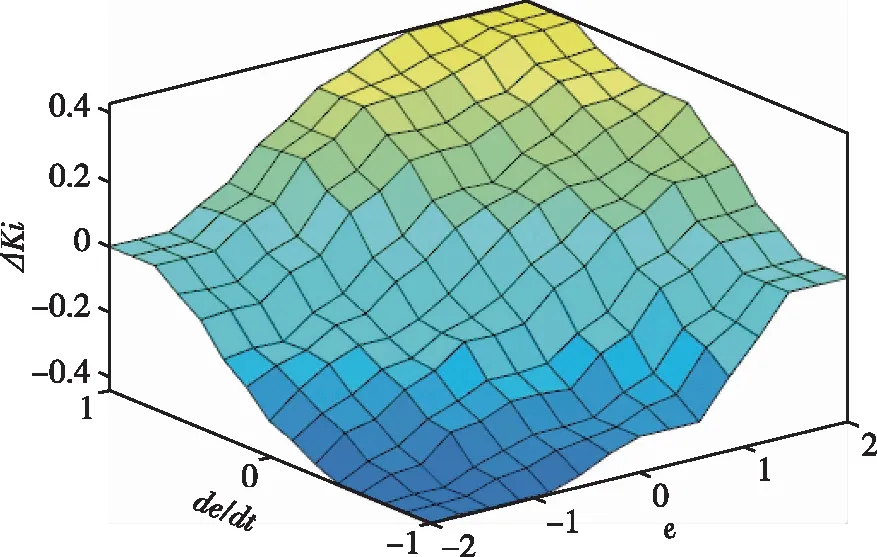
图7 ΔKi与e(t)、de(t)/dt模糊关系Fig.7 Fuzzy relation between ΔKi and e(t)、de(t)/dt

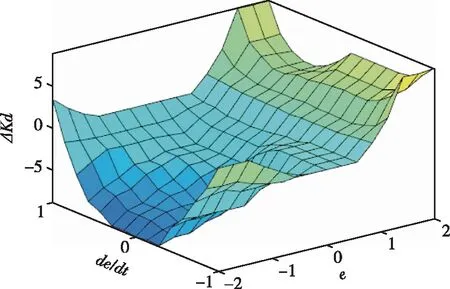
图8 ΔKd与e(t)、de(t)/dt模糊关系Fig.8 Fuzzy relation between ΔKd and e(t)、de(t)/dt

2 试验结果

为了验证本文基于模糊控制理论设计的模糊经验控制算法和模糊PID控制算法设计的有效性,将它们应用于试验场实体卸料臂中,分别进行控制算法性能对比测试和控制算法跟踪实验测试,所用试验装置——实体卸料臂充分暴露在日晒雨淋的室外环境中,如图9所示,这种在室外环境中进行的试验本身受到实际情况的诸多干扰,能够很好地验证算法在实际情况下的抗干扰性能。

图9 试验场实体卸料臂实景Fig.9 Realistic scene of the LNG unloading arm in the test site

将阶跃信号和正弦信号分别作用于如图9所示场景下的试验场实体卸料臂中,通过对阶跃信号作用下的性能指标和对正弦信号作用下的跟踪表现,验证了引入模糊控制理论对卸料臂的控制性能有明显的改善。

2.1 控制算法性能对比

控制算法性能指标测试部分对单个关节输入一个幅值为2°的阶跃信号,使该关节由静止开始运动,为了避免试验结果因关节位置发生偶然性,以回转关节为例,在不同的关节角处设置两组试验以充分验证控制算法的有效性,起始关节角分别设定为0°和8°,分别得到各个控制算法的控制效果仿真对比,如图10所示。

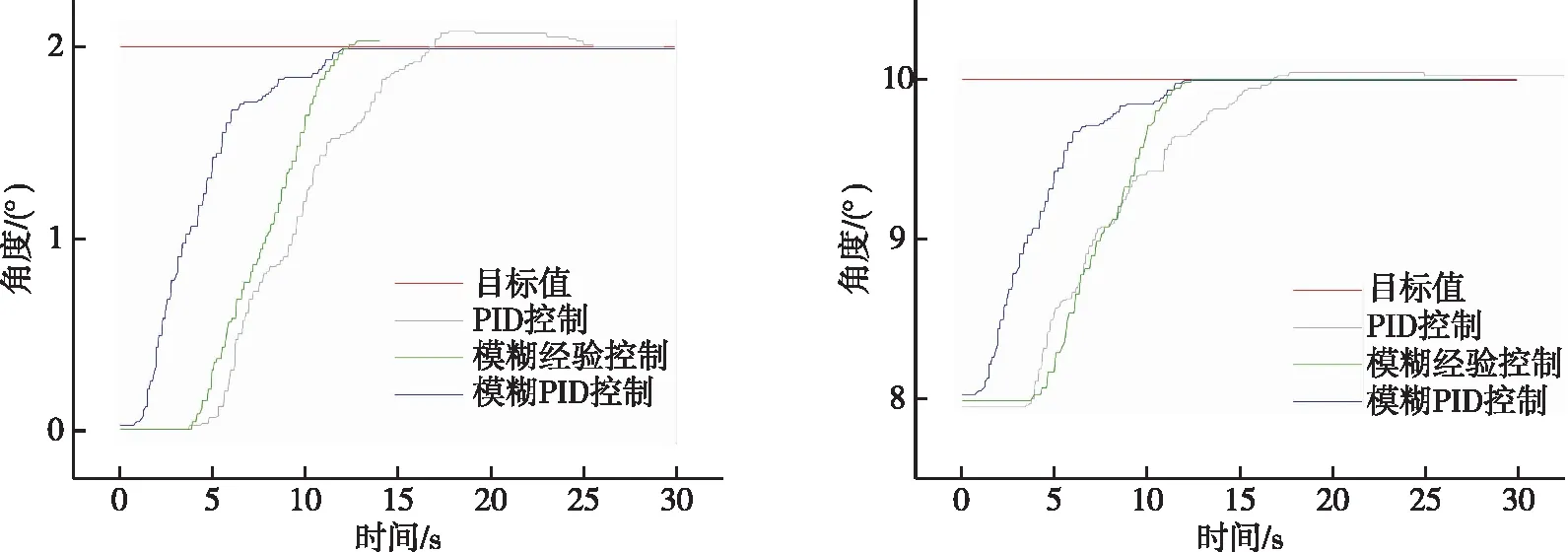
图10 回转关节控制算法控制效果(左图为起始角设定为0°时的试验,右图为起始角设定为8°时的试验)Fig.10 Control effect of joint 1 (The left figure shows when the starting angle is 0°, and the right figure shows when the starting angle is 8°)

由图10可以看出,控制算法在不同关节角度处的控制效果基本相同,控制曲线的形状基本一致,可以验证控制算法的控制效果受卸料臂关节所处位置的影响较小,具有很强的通用性,因此在性能测试中无须考虑关节所处位置对控制算法控制效果的影响。

其他关节同样经过了上述结论的验证,两组试验取平均后的回转以及其他关节的性能指标参数如表5所示。可以看出,从引入模糊控制理论的两种控制算法与PID控制算法的对比上来看,引入模糊控制理论的两种控制算法,相比PID控制算法,既减小了超调量,又缩短了调节时间,性能得到了明显提升。从两种控制算法之间的对比上来看,性能指标比较相似,但由图10可以看出,在抵抗由于绳子收缩所带来的时延问题上,模糊PID控制更佳,然而在绳子收紧启动后的响应上,模糊经验控制又能通过其快速性很好地弥补其自身由于时延而造成的滞后性,从而造成了两种控制算法在性能指标上的表现上具有相似性。

在实际的应用中,若采用模糊经验控制这种抗时延能力弱,但在启动后响应比较剧烈的算法,极有可能造成的结果是卸料臂的运动不流畅,即产生一顿一顿的效果,不仅影响观感,而且由于频繁地加速减速还会造成结构件过快损耗,而模糊PID控制算法则运行更柔和,在不牺牲算法性能的前提下,能够让卸料臂的运动流畅顺滑,对卸料臂本身及其结构件更友好。

因此,总体来说,模糊经验控制和模糊PID控制两种算法虽然在性能上不分伯仲,但在实际应用中,模糊PID控制算法具有更好的控制效果。

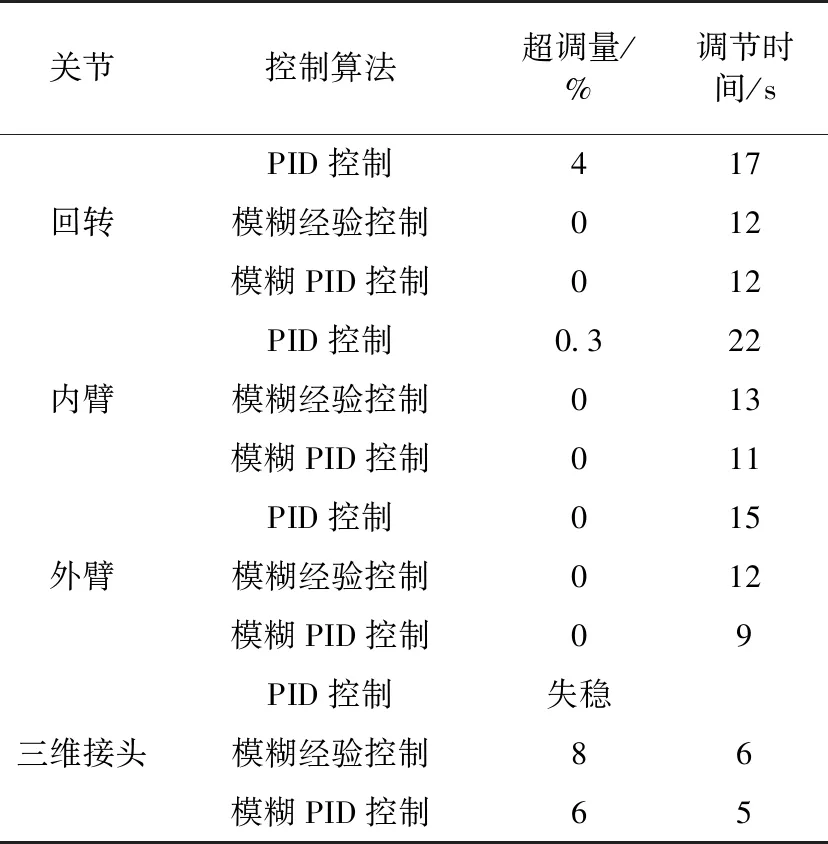
表5 输入幅值为2°的阶跃信号时控制算法性能参数

2.2 控制算法跟踪实验

控制算法跟踪实验测试部分将通过一个固定周期的正弦信号近似模拟受海面波浪影响而目标法兰发生移动的情况,这种移动一般不会过于剧烈,因此该部分对单个关节输入一个幅值为[1,2](单位:°)区间内的随机数,周期为80 s的正弦信号进行跟踪测试,使该关节由静止开始运动,如同性能测试试验一样,为了避免试验结果因关节位置发生偶然性,以回转关节为例,起始关节角分别设定为0°和8°,分别得到各个控制算法的跟踪效果,如图11所示。

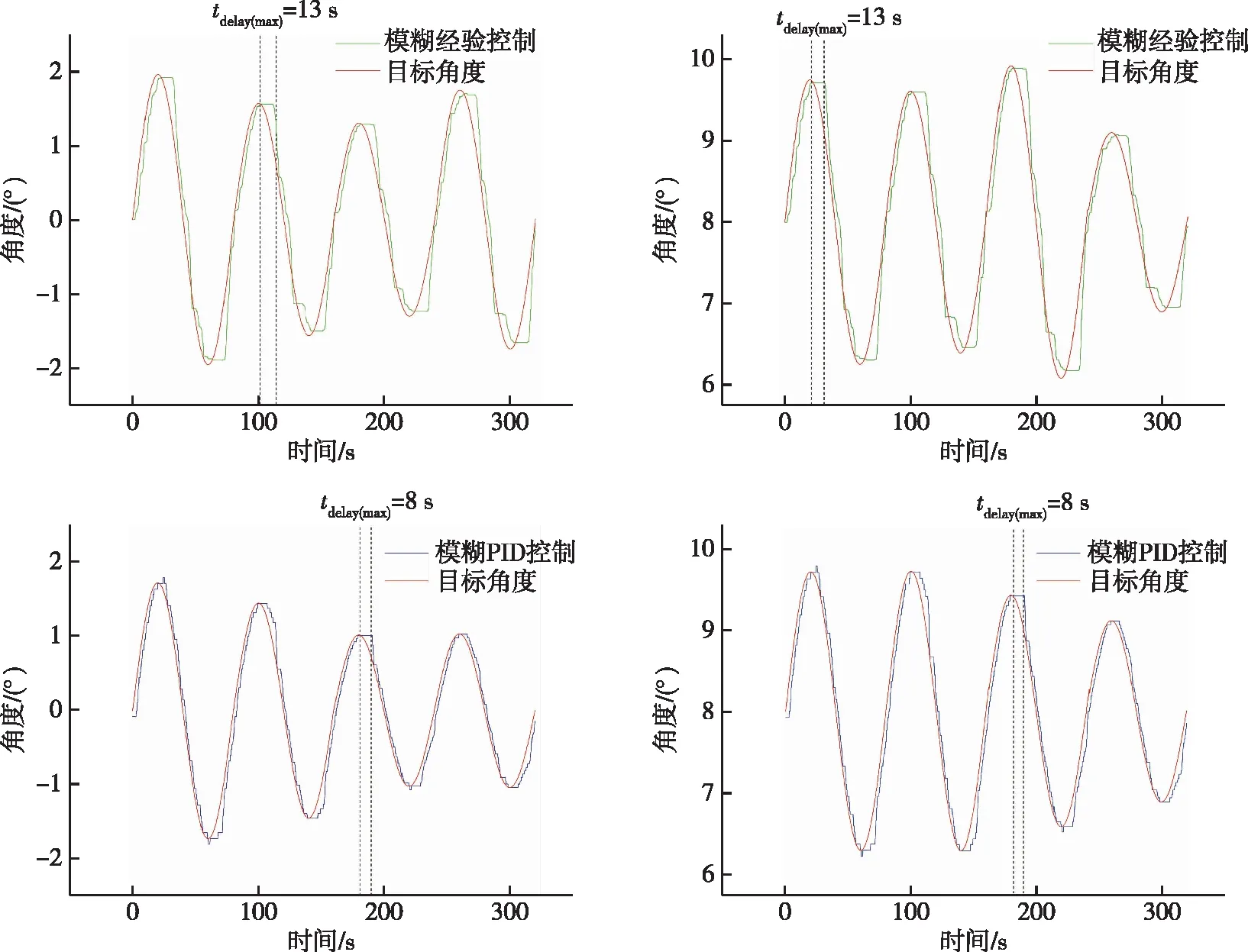
图11 回转关节控制算法跟踪效果Fig.11 Tracking effect of joint 1

在图11中,左上图为起始角设定为0°时采用模糊经验控制算法的试验,跟踪时延的最大值tdelay(max)出现在正弦信号第二个周期的波峰位置,右上图为起始角设定为8°时采用模糊经验控制算法的试验,tdelay(max)出现在正弦信号第一个波峰的位置,左下图为起始角设定为0°时采用模糊PID控制算法的试验,tdelay(max)出现在正弦信号第三个波峰的位置,右下图为起始角设定为8°时采用模糊PID控制算法的试验,tdelay(max)出现在正弦信号第三个波峰的位置。总体来说,当正弦信号输入时,采用模糊经验控制算法和模糊PID控制算法皆能实现很好的跟踪,跟踪时延的最大值tdelay(max)主要出现在关节换向时,在模糊经验控制作用下,最大跟踪时延约为13 s,在模糊PID控制作用下,最大跟踪时延约为8 s,相比较而言,模糊PID控制的跟踪性能稍优于模糊经验控制。

综合以上算法性能测试和跟踪测试,模糊经验控制算法和模糊PID控制算法在总体性能上皆优于传统PID控制算法,并且在抵抗时延方面,模糊PID控制算法强于模糊经验控制算法,因此,在实际工程应用中,模糊PID控制算法具有良好的控制效果。

3 结束语

本文引入模糊控制理论,从模仿人类行为的角度分别提出和实现了直接控制电磁阀开度的模糊经验控制算法和对PID参数进行实时调整以间接对电磁阀开度进行控制的模糊PID控制算法,既无须构建卸料臂的动力学模型,又在传统PID控制算法的基础上改善了其动态性能,取得了良好的控制效果,并且模糊PID控制算法以其优越的抵抗时延的能力成为了实际工程应用中的最优选择,在关节控制方面具备了实时跟踪移动目标法兰的条件。