异构偏好信息下的主客方协作式群体评价方法及应用
张发明, 牛玉飞, 王伟明
(1.桂林电子科技大学 商学院,广西 桂林 541004; 2.南昌大学 经济管理学院,江西 南昌 330031; 3.江西财经大学 工商管理学院,江西 南昌 330032)
0 引言
现实决策中,由于决策环境日趋复杂,一些大型决策问题往往较难依靠个人知识与经验进行解决,而是更多地采用群体评价方式,以提升决策科学性与决策质量[1~3]。相关研究主要围绕评价信息、评价模式及评价流程等三个方面展开。
首先,在评价信息方面,由于环境的复杂性及人类思维的模糊性,相较于传统的精确数而言,决策者愈加倾向于采用不确定信息对评价对象进行描述[4~6],如不确定语言[7]、犹豫模糊语言和概率语言等定性描述方式[8,9],以及区间灰数等定量描述方式[10,11]。然而,无论何种方式以往相关研究中的评价信息大都一致,但实际中评价者的专业与信息背景往往各不相同,从而需采用适于自身的偏好表达方式,并涉及到异构或异质偏好信息的处理。例如,TANG等[12]针对多种定性与定量描述方式共存的异质大规模群决策问题,提出基于偏好序的一致性测度方法;ZHANG等[13]提出同时包含效用值、偏好序、乘型偏好与模糊偏好关系等异质偏好结构的群决策方法;李艳虹等[14]提出基于矩阵相似性的异构群体偏好信息集结方法,通过不同转化函数将异构偏好信息统一转化为模糊偏好关系。其次,在评价模式方面,相关研究大多采用评价主方(专家)单方评价模式,较少考虑评价客方(评价对象)的参与,但大多情况下客方对自身与彼此的了解往往更加全面和具体,客方的参与能有效提升决策质量。对此,张发明等[15]提出一种新的主客方协作式群体评价模式,通过对客方意见的调整及双方意见的集结实现协作;接着,董庆兴等[16]提出一种基于“差异驱动”原理的主客体协作式综合评价方法;考虑区间数情形,张发明等[17,18]进一步提出区间诱导密度加权合成算子对双方的区间信息进行集结,并提出差异优势度来衡量评价信息优劣,以差异优势度为诱导实现双方评价信息的聚类和集结。最后,在评价流程方面,主客方协作式群体评价大致可分为以下两类:①先根据双方意见的分布提取权重或聚类信息,再进行信息集结,侧重点在于权重或优势度的确定[16,18];②根据双方意见分布对客方意见进行调整,再提取权重信息并进行信息集结,侧重点在于双方意见交互及客方意见的调整[15,17]。以上群体评价方法各有侧重,且均取得了有效研究成果。但经过梳理,大多仍存在以下不足:1)评价信息方面,异构或异质偏好信息下的群体评价问题大都未考虑客方参与,其在应用模式方面的扩展相对有限;2)评价模式方面,以往的主客方协作式群体评价大都未考虑双方采用异构偏好信息表达意见的情形;3)评价流程方面,主客双方的交互相对不充分且信息的综合修正作用相对不明显。
为弥补与改进以上不足之处,本文提出异构偏好信息下基于两次协作过程的主客方协作式群体评价方法,其主要具有以下特点。首先,考虑双方存在的信息不对称,分别采用不确定语言与区间灰数作为评价主方与客方的偏好表达方式,实现异构偏好信息与主客方协作式群体评价模式之间的优势互补。其次,综合考虑评价值局部偏差和评价向量整体偏差,在主方信息“完备度”和客方信息“诚信度”的基础上提出相应的完备度调节因子和诚信度调节因子,实现最小粒度层面上对双方评价信息的平稳修正。
1 问题描述及假设规则
1.1 问题描述
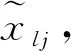
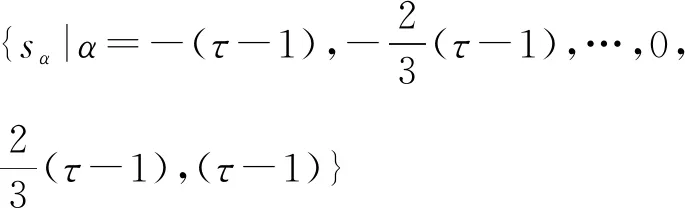
(1)
而第k(k=1,2,…,n)个客方对第j(j=1,2,…,n)个客方的评价意见则表示为区间灰数y(⊗)kj,且论域为Ω∈[a,b]。
那么,设所有主方的原始评价信息构成矩阵X;在将所有客方的原始评价信息均转化为核和灰度的形式之后,设所有客方的原始评价信息构成矩阵Y。(关于不确定语言与基于核和灰度的区间灰数,基础知识可自行查阅相关文献资料)
1.2 假设及协作规则
首先,需满足以下基本假设条件。
假设1主方具备相关专业知识,但掌握的信息没有客方全面;
假设2客方对自身和彼此都较为熟悉,但其主观性相对更强;
假设3双方都是“理性人”,并且各客方通常不会因为个人主观情感因素影响对彼此的理性判断。
其次,应遵守以下协作规则。
规则1协作之前,双方各自独立给出评价意见,不存在双方“合谋”的情形;
规则2各客方对彼此的评价是匿名的,无法得知其他客方对自己的评价意见。
2 基于两次协作过程的主客方协作式群体评价
2.1 主客方第一次协作:评价信息修正
2.1.1 主客方评价信息的协作初始得分
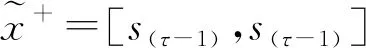
对于客方评价信息,评价值y(⊗)kj的协作初始得分为
其中,γ(⊗)kj为y(⊗)kj的基于核和灰度的相对精确集成值。其借鉴于标准灰数基于核和灰度的相对核[19],同时既简化了计算过程,又能有效保留原始信息。具体定义如下。
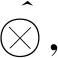
为灰数⊗的基于核和灰度的相对精确集成值。
由上,主客双方所有原始评价值的协作初始得分分别构成协作初始得分矩阵
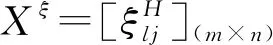
2.1.2 基于协作初始得分矩阵的信息“完备度”与信息“诚信度”
(1)主方评价值的本原调节因子与主方信息“完备度”
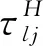
(5)
根据第l个主方所有评价值的本原调节因子,得到其评价向量的完备性偏离度
(6)
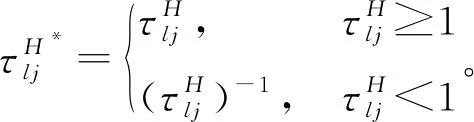
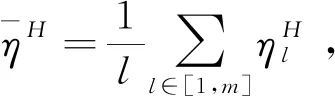
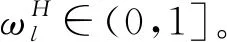
(2)客方评价值的本原调节因子与客方信息“诚信度”
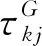
(8)
根据第k个客方所有评价值的本原调节因子,得到其评价向量的客观性偏离度
(9)
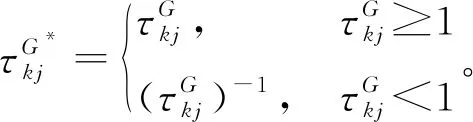
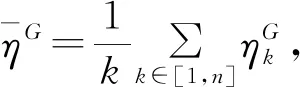
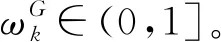
2.1.3 主客方评价信息的修正
定义2已知主方评价值的本原调节因子和主方信息“完备度”,称
为第l个主方对第j个评价对象评价值的完备度调节因子。
定义3已知客方评价值的本原调节因子和客方信息“诚信度”,称
为第k个客方对第j个评价对象评价值的诚信度调节因子。
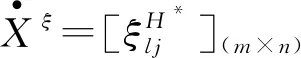
2.2 主客方第二次协作:评价信息集结
2.2.1 考虑单方与双方评价意见的TOPSIS综合贴进度
首先,求出该评价值在主方评价下的TOPSIS相对贴近度
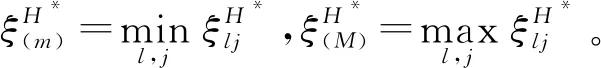
其次,求出该评价值在双方评价下的TOPSIS相对贴近度
最后,综合考虑单方和双方评价意见,求出该评价值的TOPSIS综合贴近度
其中,o1与o2分别表示单方局部信息和双方整体信息的贴近度系数,满足o1+o2=1。
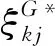
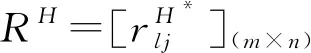
2.2.2 群组灰关联聚类
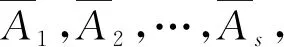
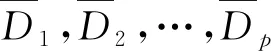
2.2.3 各单方评价信息的集结
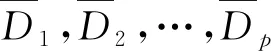
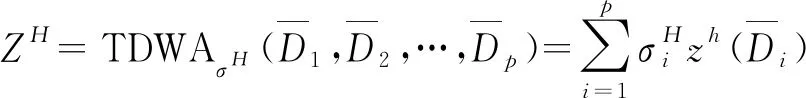
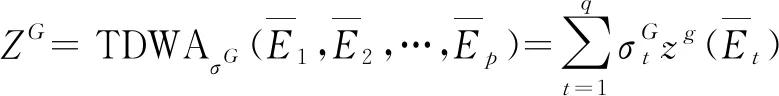
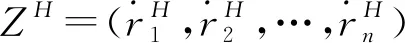
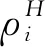
(19)
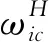
2.2.4 群组密度权重的求解及优化
此处,同样以评价主方优化的群组密度加权向量σH为例。
(1)群组密度权重求解
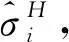
(20)
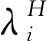
(21)
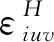
(2)群组密度权重的优化
根据极大熵原理,构建单目标优化模型Mσ对各群组密度权重进行优化,从而得到优化的群组密度加权向量σH。
其中,l为控制指数,满足l≥2。
根据以上步骤,进一步求出客方各组集合的群组密度权重,并对其进行优化。
2.2.5 主客方评价信息的集结
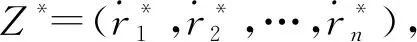
其中,ζ1和ζ2为合成系数,满足ζ1+ζ2=1。
通过对Z*中的各综合评价得分进行比较,即可得出所有评价对象的优劣顺序。
3 应用实例
某医院为从8家医疗设备供应商中选出最合适的设备供应商合作伙伴,请来该领域5名专家对各供应商进行考察和评分。同时,为使评价信息更加全面,通过访查形式展开主客方协作式群体评价。其中,所有专家构成评价主方集合H={Hi|i=1,2,…,5},供应商构成评价客方集合G={Gj|j=1,2,…,8} 。经协商,各专家采用不确定语言打分,并将τ赋为τ=4;各供应商则采用区间灰数打分,且论域为Ω∈[0,10]。所有专家和供应商的原始评价信息分别构成矩阵X和矩阵Y。
3.1 评价结果
对于各主要参数,分别将双方群组灰关联聚类中的关联度阈值设为0.85与0.95;式(15)中的贴近度系数设为o1=o2=0.5;优化模型Mσ中的控制指数设为l=4;式(23)中的合成系数则设为ζ1=ζ2=0.5。所得出的主客方综合评价得分向量为
Z*=(0.5613,0.5078,0.7879,0.4434,
0.7412,0.4377,0.3688,0.3734)。
(24)
各设备供应商的优劣次序为
G3≻G5≻G1≻G2≻G4≻G6≻G8≻G7
(25)
因此,该医院应选择供应商G3作为医疗设备采购的合作伙伴。
3.2 对比分析
为说明本文方法的合理性和有效性,在此展开对比分析。具体地,将主客方之间所有协作过程去掉,求出双方在非协作下各自独立的评价结果,并与本文方法计算结果进行对比,如表1所示。
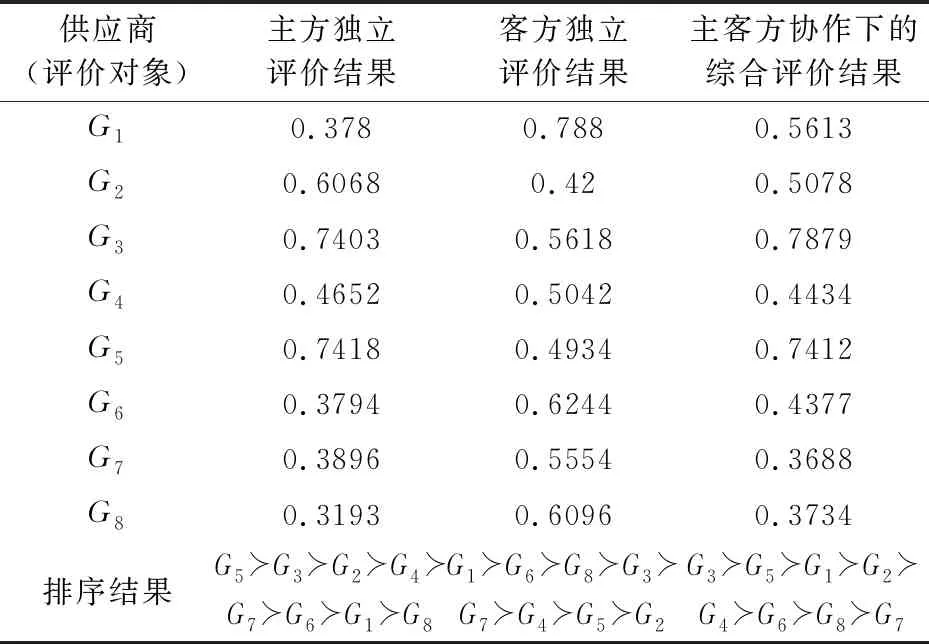
表1 主客方协作与非协作下的评价结果总览
首先,从排序结果来看,所有供应商均未出现三种情况完全一致的情形,部分供应商的优劣次序则出现了逆转,如G3,G5。其次,从数值结果来看,主客方协作下的各评价值基本都处于非协作下双方对应评价值之间,体现出双方意见的折衷。
为进一步考察双方的第一次协作对评价信息的修正作用,分别给出主客方协作和非协作下各方评价结果的柱状对比图,如图1所示。
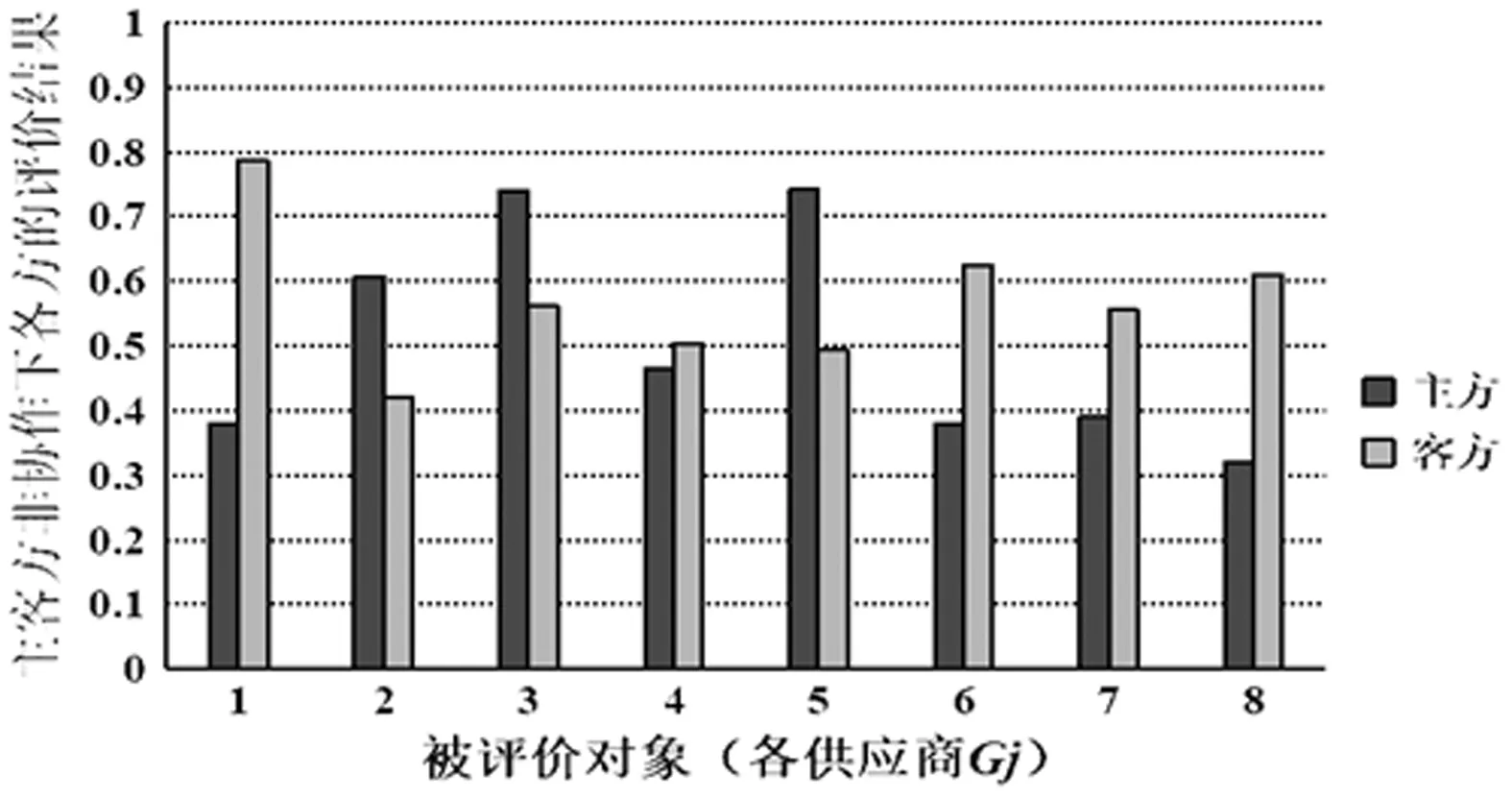
(a)主客方非协作下的各方评价结果
通过对比可以发现,双方在进行信息交互后得到了更为一致的评价结果。相较于非协作下主客方各自的独立评价结果,两次协作使原始评价信息得到深度利用,并有效实现异构偏好意见的交互与融合。
4 结语
目前,异构或异质偏好信息下的群体评价问题大都未考虑客方的参与,且既有的主客方协作式群体评价均未考虑双方采用异构偏好表达方式的情形。对此,本文提出一种异构偏好信息下的主客方协作式群体评价方法,通过两次协作过程实现双方评价意见的交互与融合。本文的主要工作如下。
(1)分别采用不确定语言和区间灰数来描述主客双方的偏好意见,实现了异构偏好表达与主客方协作式群体评价模式之间的优势互补,增强了偏好表达方式的多样性与评价对象的参与积极性;(2)在主客方的第一次协作过程中,分别提出信息“完备度”、信息“诚信度”及相应调节因子,从而实现最小粒度层面上对双方原始评价信息的修正,深化了修正作用水平;(3)在主客方的第二次协作过程中,综合运用TOPSIS、灰关联聚类与TDWA算子实现双方评价信息的聚类和集结,克服了协作成分不足的缺陷,实现了双方意见的渐进有机融合。
实例应用与对比分析结果表明,所提方法可有效实现异构偏好信息下双方意见的交互与融合,一定程度上提升了评价结果的合理性和稳定性。不过,该方法主要适用于评价客方具有主观能动性的情形,要求不能与人无关或不具有主观意识,将来则可进一步开展研究,实现不同应用场景下的拓展。

