跨流域供水水库群联合调度的半向量双层规划模型研究

吕一兵, 万仲平, 胡铁松, 郭旭宁

(1.长江大学 信息与数学学院,湖北 荆州 434023; 2.武汉大学 数学与统计学院,湖北 武汉 430072; 3.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072; 4.水利部水利水电规划设计总院,北京 100120)

0 引言

跨流域水库群联合调度包含两个方面的研究内容,一是水库群联合供水调度规则的确定问题;二是跨流域调水问题[1]。在水库群联合供水调度规则方面,曾祥等[2]建立了并联供水水库系统调度规则优选的模拟-优化模型;郭旭宁等[3]提出了配合变动分水系数的二维水库调度图模型;曾祥等[4,5]研究了并联水库群联合调度规则的最优性条件。在跨流域调水方面,王国利等[6]以追求“满意决策”为目标,构建了跨流域调水方案优选的多目标决策协商模型;赵静等[7]采用层次分析和效用函数计算模型相结合的方法,优选跨流域调水方案。

值得指出的是,上述关于水库群联合供水调度规则的研究,没有将水库供水与跨流域调水统一考虑,这对于水资源的时空配置效率势必产生不利影响;另外,有关跨流域调水问题的研究,更多的局限于调水方案和调水规模,对跨流域调水规则却极少涉及。事实上,在跨流域供水水库群联合调度中,调水规则与供水规则的确定是相互联系的两个过程,只有联合考虑才能得到最优的调度方案。

万文华等[8]构建了同时考虑调水和供水的复杂水库群联合优化调度模型;在笔者前期研究中[9],构建了跨流域供水水库群联合调度的双层规划模型。值得指出的是,在上述跨流域供水水库群联合调度的双层规划模型中,上层决策者(水资源管理机构)处于支配地位,能够影响下层决策者(各水库管理者)做出对自己最为有利的决策。因此,本文考虑采用水库对各用水户的期望供水质量与实际供水质量的差值最小为下层决策者的目标函数,即下层为多目标规划,构建跨流域供水水库群联合调度的半向量双层规划模型,并求其“乐观最优解”,以得到最优的调水和供水规则。

1 跨流域供水水库群联合调度的半向量双层规划模型

1.1 半向量双层规划

半向量双层规划是上层为单目标,下层为多目标的一类双层规划问题[10,11]。在半向量二层规划中,下层以有效解集反馈给上层。由于有效解集的元素一般不是唯一的,这就意味着半向量双层规划本质上为下层有不唯一最优解的双层规划问题。对于该类双层规划问题,其最优解定义采用“乐观最优解”或“悲观最优解”[12]。本文考虑其“乐观最优解”。

1.2 调水与供水规则的表述

本文以“一主两副”跨流域三库供水水库群为例,阐述水库群联合调水供水规则。如图1所示,调水工程由分处于不同流域的三个水库构成:水源水库②所处流域水量丰沛,可向外调水;而受水水库①、③所处流域水资源难以支撑区域社会经济发展,于是水库②在满足本流域需水的同时,向水库①、③调水。

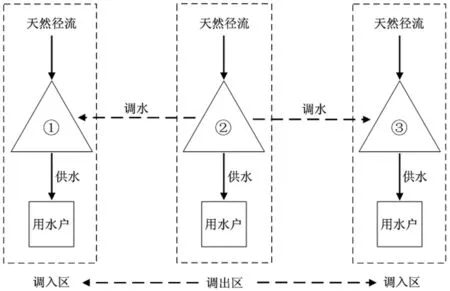
图1 “一主两副”跨流域供水水库群水力联系示意图

如图2所示,本文采用基于水库蓄水状态的调水控制线来表示调水规则[9]。即各库蓄水量和调度线的相对位置可判断水源水库②什么时候向外调水,调多少水,调水量如何在水库①、③之间进行分配。

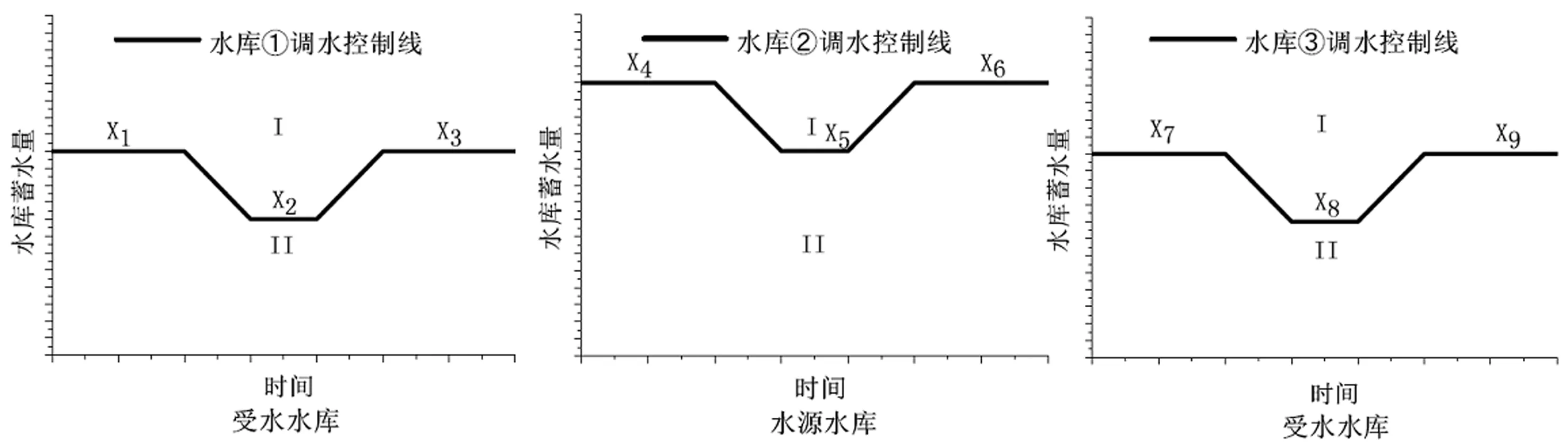
图2 跨流域调水水库群水力联系示意图

调度图是指导水库运行的重要工具之一。本文中,调度图由分别对应于不同用水户的多根限制供水调度线构成,如图3所示。根据供水目标的优先级和设计供水保证率高低,限制供水线由下至上依次排列并将兴利库容分成若干调度区。水库运行过程中,根据水库蓄水量所处调度区的供水规则分别对各用水户供水。

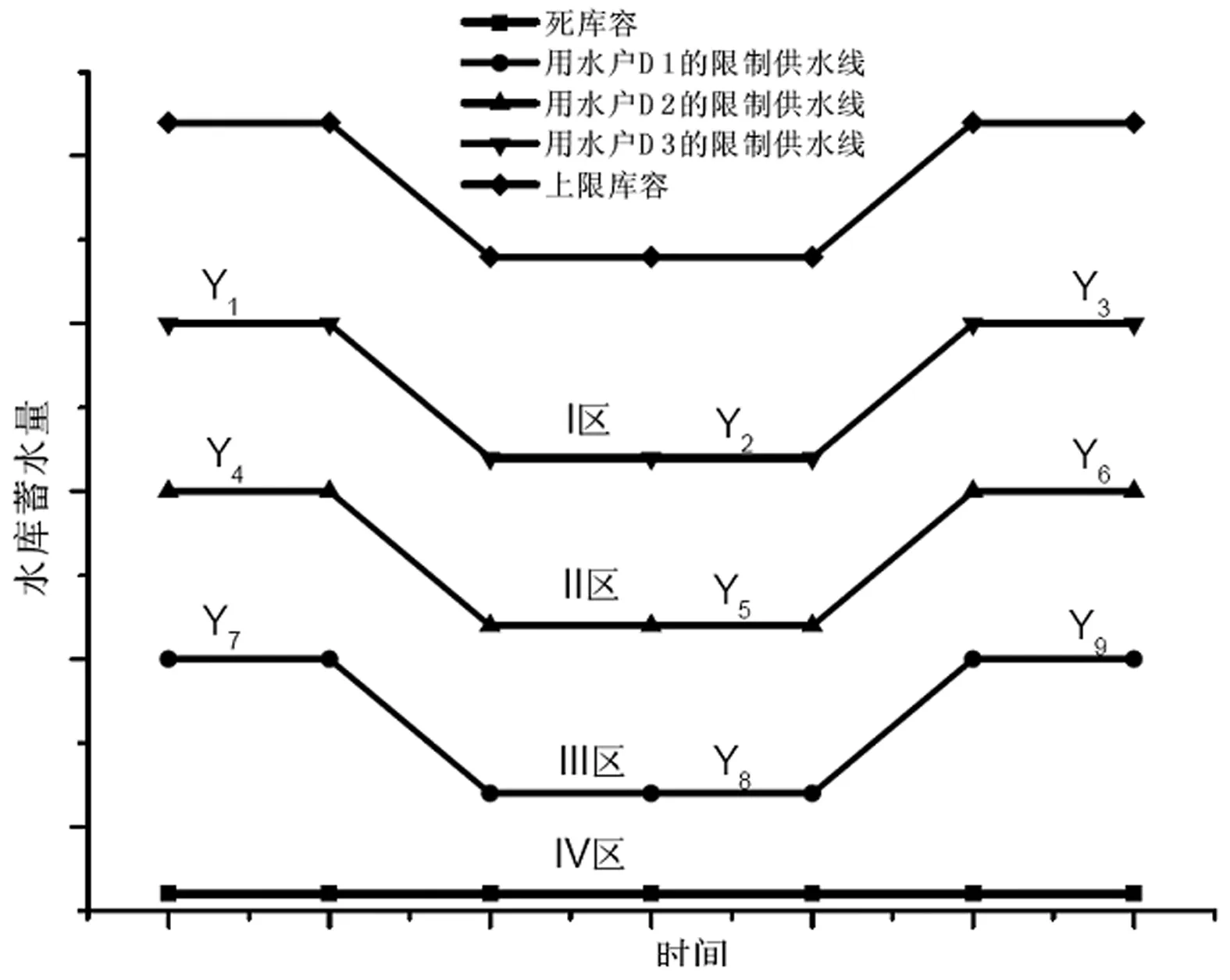
图3 水库供水调度图示意图

1.3 模型的构建

1.3.1 上层调水模型

调水规则由一组调水控制线来表述,如图2所示,主要反映调水时库群水库间的动态关系,其调水规则为:(1)当水源水库的水量高于其调水控制线时,表示可以将蓄水量外调。为了避免外调水量转化为弃水,必须关注受水水库蓄水状况,可以分三种情况。一是,水库①和水库③的实际蓄水量均低于其调水控制线,即两个水库的蓄水量偏少,可以对两个水库进行调水;二是,水库①和水库③中的某一个水库需要调水,而另外一个不需要调水;三是,水库①和水库③的实际蓄水量均高于其调水控制线,都不需要进行调水。(2)当水源水库的水量低于其调水控制线时,表示没有水量可以外调。此时,无论水库①和水库③的蓄水状况如何,都不进行调水。

由上所述,将调水控制线作为上层调水模型的决策变量,而取接近流域间预期调配水量和各受水水库弃水量最小为上层目标函数,上层调水模型可以表述为:

s.t.NDSi=G(x,y),SUi=g(x,y),

(1)

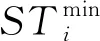
1.3.2 下层供水模型

如1.2所述,供水规则由各库供水调度图表示,而调度图又由不同用水户的限制供水线表示。自下而上排列的限制供水线将水库的兴利库容分为了若干调度区,同时根据蓄水量所处的调度区对应的供水规则对用水户进行供水。在下层供水模型中,取各用水户的期望供水质量与实际供水质量的差值最小为目标函数。下层供水模型可以表述为:

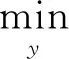
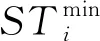
因此,所构建的跨流域供水水库群联合调度的半向量双层规划模型可以表述为:

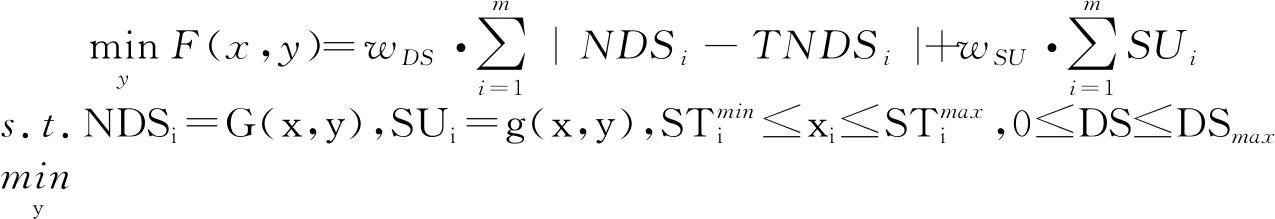
(3)

在上述半向量双层规划模型(3)中,上层决策者处于支配地位,能够影响下层决策者做出对自己最为有利的决策。因此,可以引入权重变量λij作为上层决策者的决策变量,从而将模型(3)转化为:

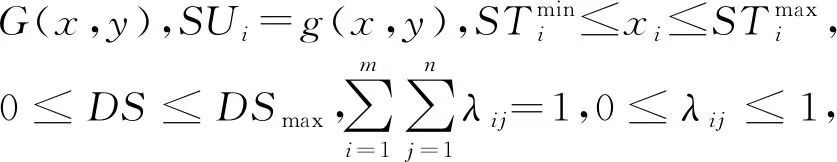
(4)

值得指出的是,在文献9中权重λij为给定的常数,而在模型(4)中将权重λij作为上层决策者的决策变量。通过优化算法确定权重λij更有利于得到最优的调水和供水规则。

1.4 模型的求解

在模型(4)中,目标函数与决策变量之间的函数关系是通过模拟水库群长时序的调水、供水过程,经过统计而得出的,没有具体的函数表达式[9]。因此,基于模拟-优化求解模式,并采用并行种群混合进化的粒子群算法对模型(4)进行求解,其参数设置为6个并行种群、每个种群粒子数目为50个。具体求解流程可参照文献9中粒子群算法的实现过程。

2 应用算例

为了分析所建模型对跨流域水库群调水供水问题的适用性,本文提出了四种调水情境,比较不同情境下的调度结果差异与调水供水规则响应,如表1所示。

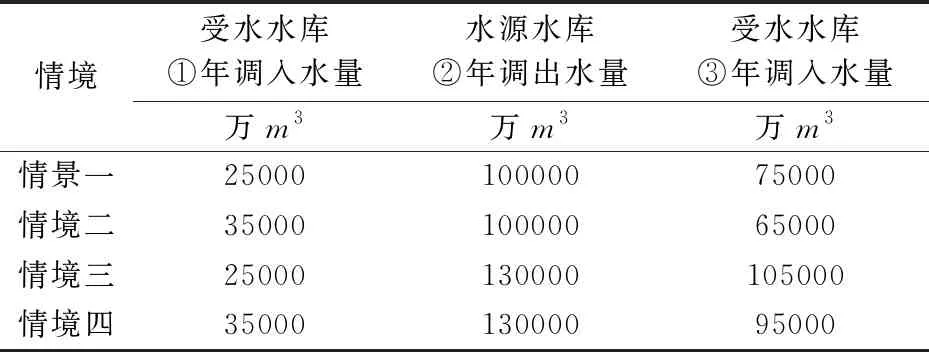
表1 用于分析半向量双层规划模型适用性的四种调水情境

为了实现流域间的水量分配目标,以水库②年均调出水量与水库①分配水量为上层模型的调水目标,进而得到与之相匹配的调水规则。对于本文提出的用以表达水库群调水规则的调水控制线,它们在不同时段的位置决定了调水规则的具体内容。针对确定的不同调水目标,相应的调水控制线是否会做出合理的响应,调水控制线的位置变化是否合乎一般规律是判断模型是否合理的依据。

由于一组调水控制线之间彼此关联,需要相互配合来表达一种调水规则,因此对于确定调水目标的调水控制线位置应该是不唯一的。本文将调水控制线把水库兴利库容分成的上下两部分(I区与II区)的面积作为反映调水控制线位置高低的评价指标,对不同调水情境下的调水规则进行比较,如图4所示。分析水库①的调水控制线,可以发现情境二II区比情境一II区的面积明显变大;水库③的调水控制线,情境二II区比情境一II区的面积变小。对于受水水库,II区的面积变大意味着调入水的几率变大,II区面积变小允许的调入水量会变少。受水水库调水控制线的这种变化是对情境一、二受水水库目标调入水量进行调整的合理响应。值得指出的是情境三、四也存在类似现象。限于篇幅,本文不再列出情景三和四的调水控制线变化情况。

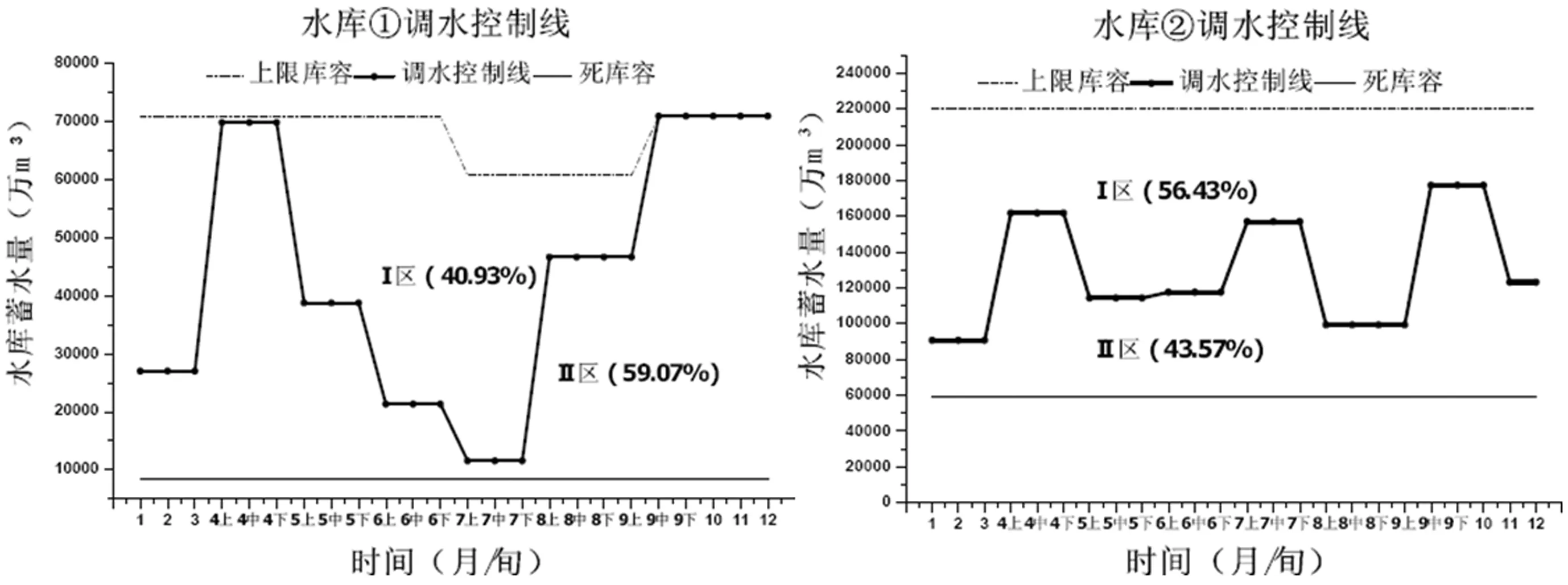
(a1)情境一水库①和②调水控制线

四种情境下,随着水库③年调入水量的增加,水库③调水控制线II区的面积逐渐变大,这种变化趋势符合一般规律。水库②的调水控制线在不同情境下保持着基本稳定,说明外调水量规模的变化可以通过受水水库调水控制线的变化实现,体现了三根调水控制线之间的相互联系关系。下层模型以广义缺水指数GSI作为评价指标(缺水指数越小代表用水户的供水质量越好),不同调水情境下各水库主要用水户供水质量列于表2。对于水库②,它的用水户在情境一、二下的缺水指数相接近,并小于情境三、四下的缺水指数,这与情境三、四的外调水量增加有关。同样的规律出现在水库①、③的调度结果中,当受水水库的调入水量增加时,用水户的缺水指数会变小,表明供水效果得到改善。这也表明所建模型是合理的。

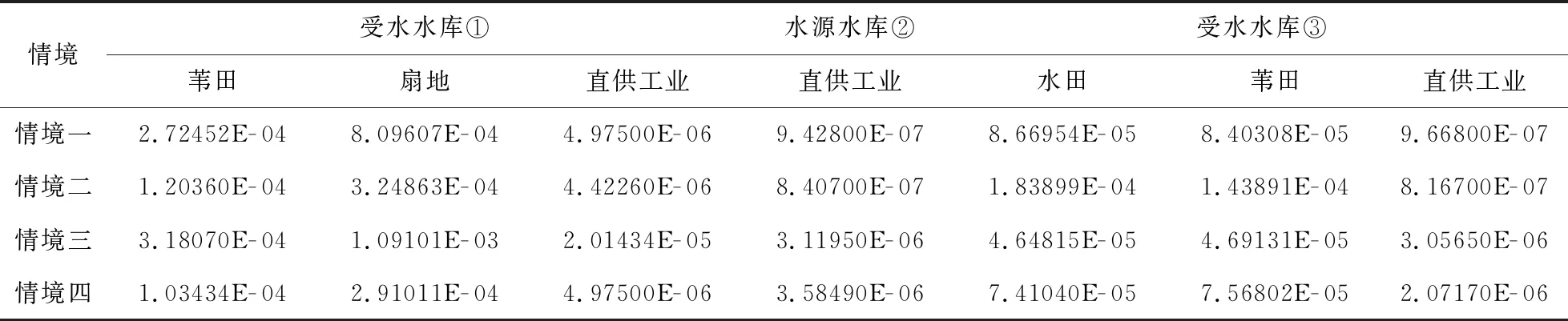
表2 不同调水情境下各水库主要用水户供水质量比较(广义缺水指数,GSI)

进一步,为了分析所建立的半向量双层规划模型与前期建立的一般双层规划模型在求解跨流域供水水库群联合调度问题时的表现差异,通过设定相同的目标函数指标和迭代次数,在近100次模型运行中,有近90次半向量双层规划模型运行结果优于一般双层规划模型,各水库主要用水户广义缺水指数普遍降低15%～25%,具体结果见表3。

表3 同种调水情境下半向量与一般双层模型主要用水户供水质量指标计算平均值比较

3 结论

本文构建了跨流域供水水库群联合调度的半向量双层规划模型,并求解其“乐观最优解”,以得到最优的调水和供水规则。通过应用算例,着重将所构建的半向量双层规划模型与一般的双层规划模型进行了对比分析,证实了所建立的半向量双层规划模型更有利于得到最优的调水、供水规则。