基于余弦相似度的多模态模仿学习方法
郝少璞 刘 全,2,3,4 徐平安 张立华 黄志刚
1 (苏州大学计算机科学与技术学院 江苏 苏州 215006)
2 (软件新技术与产业化协同创新中心(南京大学)南京 210023)
3 (符号计算与知识工程教育部重点实验室(吉林大学)长春 130012)
4 (江苏省计算机信息处理技术重点实验室(苏州大学)江苏 苏州 215006)
模仿学习[1-2](imitation learning,IL)在不显式设计强化学习奖赏信号的情况下,从专家样本中模仿专家策略.近年来模仿学习已经成功应用于自动驾驶、机器控制和自然语言处理等领域,并成为人工智能领域研究的热点之一.模仿学习方法包含行为克隆方法[3]和逆向强化学习[4-5](inverse reinforcement learning,IRL)方法.
行为克隆方法无需设定奖赏函数,使用经典的监督学习方法建立从状态到动作的映射函数,不需要与环境交互即可学习专家策略.由于行为克隆方法难以准确表征复杂状态—动作空间中的映射关系,导致其在复杂连续状态空间任务中表现不佳.逆向强化学习方法从专家样本中学习奖赏函数,构建马尔可夫决策过程,并利用强化学习方法学习专家策略.与行为克隆方法相比,逆向强化学习方法中不存在复合误差问题,且具有较好的鲁棒性与泛化性.
Ho 等人[6]将生成对抗网络[7](generative adversarial network,GAN)中的极小极大博弈思想应用到模仿学习中,提出了生成对抗模仿学习(generative adversarial imitation learning,GAIL)方法.GAIL 从占有率度量的角度出发,以最大因果熵为正则化项,通过极小极大博弈的方式,解决模仿学习问题.与传统逆向强化学习方法相比,GAIL 在解决大规模的模仿学习问题时,具有优异的性能[8].
GAIL 使用JS(Jensen Shannon)散度衡量专家策略与当前策略之间的差异,并通过最小化该差异,促使当前策略逼近专家策略.但是使用JS 散度作为度量方式可能会导致策略出现梯度消失问题.针对该问题,Zhang 等人[9]以f-散度作为度量方式提出了GAIL的变体:学习f-散度的生成对抗模仿学习(learningf-divergence for generative adversarial imitation learning,f-GAIL).f-GAIL 自动从f-散度家族中学习最优差异度量,并学习一种能够产生专家行为的策略.此外,Zhang等人[10]提出一种基于Wasserstein 距离的对抗模仿学习方法(Wasserstein distance guided adversarial imitation learning,WDIL).该方法不仅引入Wasserstein 距离,使对抗训练过程中获得更适合的度量,而且通过探索奖赏函数的形状适应不同的任务,进一步提升方法的性能.
GAIL 及其大部分扩展方法都假设专家样本来自单一模态策略,忽略了专家策略由多个模态构成,导致智能体学习到的策略难以满足专家策略的多样性.f-GAIL 和WDIL 方法虽然在绝大部分模仿学习任务中表现不俗,但均未考虑模式塌缩问题.在GAIL中鉴别器负责计算样本来自专家样本分布的概率,而策略负责与环境交互,产生趋近专家样本分布的状态-动作对.在策略更新过程中,策略倾向于朝着更容易欺骗鉴别器的若干个模态的方向进行更新,而忽略不易于欺骗鉴别器的模态,这便是GAIL 中出现模式塌缩问题的原因.
近年来,为了解决GAIL 中的模式塌缩问题,针对生成对抗框架[11-13]提出了大量的改进.Merel 等人[14]对GAIL 进行改进,提出了条件生成对抗模仿学习(conditional generative adversarial imitation learning,CGAIL).CGAIL 将模态标签加入专家样本数据中,并在策略训练过程中使用模态标签作为条件约束,学习专家样本中的多模态数据.CGAIL 虽然使用模态标签作为指导,解决模式塌缩问题,但并没有考虑使用专家样本中的抽象特征.Lin 等人[15]提出利用辅助分类器区分模态的GAIL 方法,即基于辅助分类器的生成对抗模仿学习(generative adversarial imitation learning with auxiliary-classifier,ACGAIL).ACGAIL在CGAIL 基础上引入辅助分类器,有效利用了不同模态专家数据中的抽象特征.ACGAIL 虽然引入模态的特征来区分不同模态策略,但分类器通过共享参数与鉴别器协作,导致分类器和鉴别器之间的更新可能会互相影响.Li 等人[16]基于最大互信息原理提出基于互信息最大化的生成对抗模仿学习(information maximizing generative adversarial imitation learning,InfoGAIL).InfoGAIL 在模态标签信息未给定的情况下,通过互信息最大化识别专家样本中的显著因素,然后使用这些显著因素学习多模态专家策略.Wang等人[17]受到基于变分自编码器的生成对抗网络[18]VAE-GANs 的启发,将变分自编码器(VAE)与GAIL结合,提出了基于变分自编码器的生成对抗模仿学习VAE-GAIL.InfoGAIL 和VAE-GAIL 虽然使用不同的方式推断模态标签,但是两者都在不考虑任务上下文和语义信息的情况下区分潜在模态标签,导致推断出的模态标签并不能完全表征真实的专家样本.
大部分基于GAIL 的方法利用已有专家样本模态标签,或由推断出的模态标签来区分多种模态策略.但是这些方法使用单一策略对模态进行区分,在训练过程中不同模态策略共享网络参数,导致不同模态策略之间的更新相互影响.而且,这些方法仅仅建立了模态标签到相应专家策略的映射,而没有利用模态特征之间的关系.为了更好地解决模式塌缩问题,提出了基于余弦相似度的多模态模仿学习方法(multi-modal imitation learning method with cosine similarity,MCS-GAIL).MCS-GAIL 使用余弦相似度衡量不同模态专家样本间的特征关系,并引入多个策略学习多模态的专家策略,提高不同模态策略间的区分度.此外,余弦相似度可以提高当前策略分布对专家策略分布的拟合程度,使当前策略组能够更好地学习到不同模态的专家策略.
本文主要贡献有3 点:
1)提出一种新的生成对抗模仿学习框架,该框架使用策略组代替单一策略来学习模态信息.在模仿学习过程中,利用预训练的编码器提取样本的特征向量,并根据特征向量计算余弦项,以余弦项作为约束来更新策略组.
2)根据新的生成对抗模仿学习框架,提出了一种新的极小极大博弈公式,并通过理论分析,证明了所提方法的收敛性.
3)在2 个经典的模仿学习实验平台上,将MCSGAIL 与现有解决模式塌缩的方法进行对比,验证了MCS-GAIL 的优越性.
1 背景知识
1.1 强化学习
强化学习[19-20](reinforcement learning,RL)过程是智能体与环境进行交互,学习最优决策的过程.智能体依据现有策略采取动作,从环境中获得奖赏,同时转移到下一个状态.强化学习方法利用马尔可夫决策过程(Markov decision process,MDP)对强化学习过程进行建模,定义有限空间下的马尔可夫决策过程为四元组(S,A,R,γ).
1)S表示状态空间,st∈S表示在时刻t智能体所处的状态.
2)A表示动作空间,at∈A(s)表示在时刻t智能体所选择的动作.
3)R:S×A→R表示奖赏函数.对于任意st∈S,at∈A(s),其奖赏值可以表示为r|st,at),其中r表示智能体在状态转移后得到的环境反馈奖赏,P(st+1,r|st,at)表示智能体位于状态st采取动作at时转移到状态st+1并得到奖赏r的概率.
4)γ ∈[0,1]为折扣因子,表示未来奖赏对当前状态的重要性程度.γ越小,未来奖赏对当前状态的累积奖赏影响越小,反之则越大.
强化学习的目标是通过最大化累积折扣奖赏求解最优策略 π*.为了更好地评估策略性能,在策略训练过程中,通常使用状态函数或动作函数评估策略的累积折扣奖赏.定义状态函数值为Vπ(s)=其中T表示智能体与环境交互到达终止状态的时刻.定义动作函数为Qπ(s,a)=为了减小方差、提高策略的学习效率,将策略的优势函数[21]定义为Aπ(s,a)=Qπ(s,a)-Vπ(s).在策略更新过程中,智能体一般使用负的价值函数(状态函数、动作函数或优势函数)作为策略损失.将从开始时刻到终止时刻,智能体与环境交互的完整过程称为1 个情节,另外,用 τ表示1个情节的状态-动作对顺序序列.将1 个情节奖赏的和记为回报.
1.2 GAIL
模仿学习的目的是在没有人工设定奖赏函数的情况下,学习与专家样本分布的尽可能相似策略.早期的模仿学习方法表征方式和奖赏函数的设定都比较简单,而且奖赏函数设置通常由人工经验选取,所以早期模仿学习方法存在表达能力有限、实现难度大、训练不稳定等问题.
GAN 是一种通过对抗性过程估计生成样本分布的方法,其主要由生成器G和鉴别器D这2 个组件构成.生成器负责根据输入的噪声z,生成趋近专家样本分布的新样本;鉴别器负责判别样本为真实样本的概率.GAN 是一个极小极大博弈过程,通过不断地更新迭代,使鉴别器难以判断生成器输出的样本是否为真实样本.对GAN 进行极小极大博弈的公式为
其中pz(z)为输入鉴别器的先验噪声分布,pdata(x)为训练样本的分布.
GAIL 方法结合GAN 与模仿学习,将模仿学习过程抽象为求解奖赏函数的逆向强化学习过程和求解最优策略的强化学习过程.GAIL 示意图如图1 所示,在强化学习过程中,智能体与环境进行交互,采样得到状态-动作对样本.一方面,这些样本被用来求解奖赏函数,进一步利用奖赏函数构建优势函数,智能体使用优势函数作为损失更新策略.另一方面,将这些样本作为采样样本,用于鉴别器的后续更新.在逆向强化学习过程中,使用存储的采样样本和专家样本作为输入更新鉴别器,提高鉴别器区分专家样本与采样样本的能力.在GAIL 中,智能体采集的状态-动作对等价于GAN 中生成器的输出.与GAN 模型不同,GAIL 中的鉴别器不仅负责区分采样样本和专家样本,而且需要根据鉴别器计算的概率值求解奖赏函数.GAIL 通过进行强化学习过程与逆向强化学习过程的交替迭代,最终得到最优策略.
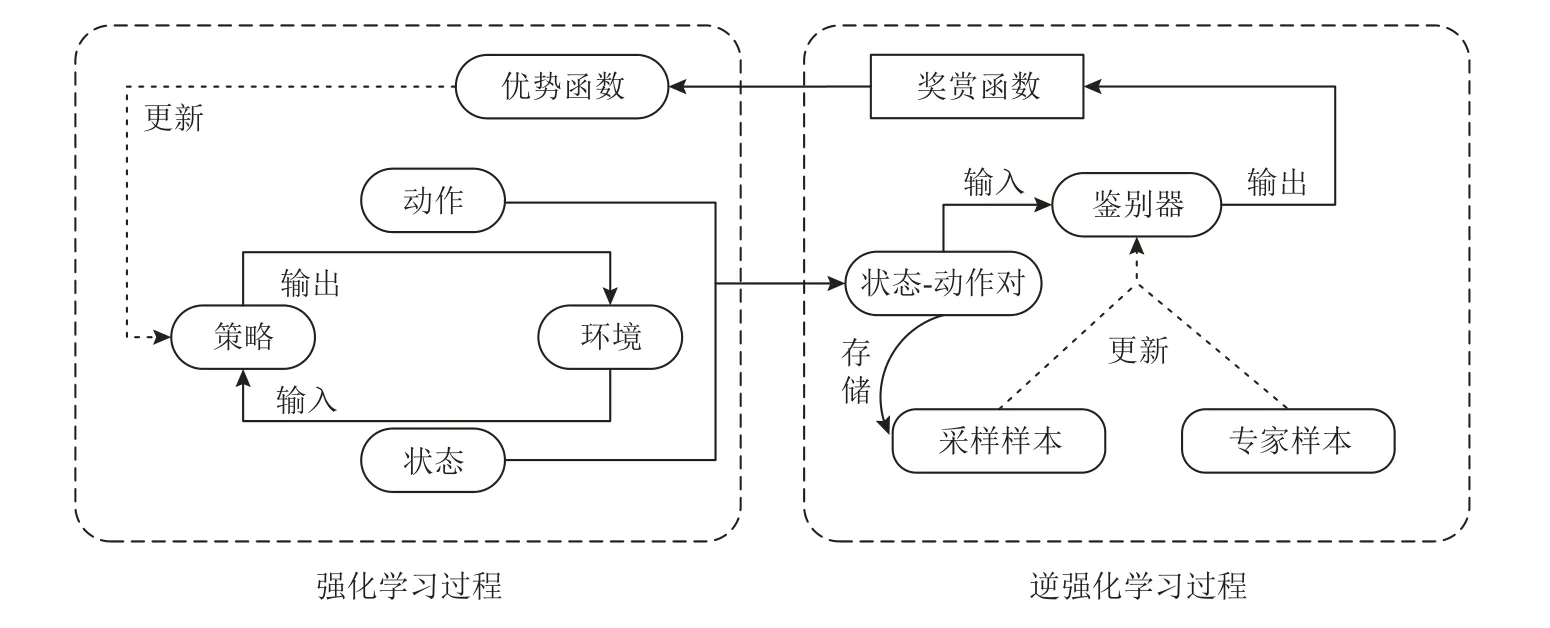
Fig.1 Illustration of GAIL图1 GAIL 示意图
GAIL 进行极小极大博弈的公式为
其中,π为智能体的策略,负责指导智能体与环境交互.D为 鉴别器,负责区分专家样本与采样样本;pe为已知的专家样本的分布;H(π)≜Eπ[-logπ(a|s)]表示将策略的因果熵作为正则化项(在状态s下 选择动作a的概率分布熵);η为熵正则化系数.为了简明表达,后续部分基于GAIL 架构的公式中均省去了H(π)项.在求解最优策略的过程中,为了构建完整的MDP 四元组,更新策略 π,定义奖赏函数为r=-log(1-D(s,a)).通俗地理解,策略采样样本分布越接近专家样本分布pe,则由鉴别器给出该样本来自专家样的概率值越大,奖赏值r越大.
1.3 多模态模仿学习
GAIL 假设专家样本由单一模态的专家策略产生,即单一风格的专家策略.实际上,专家策略可能由多个不同风格的子策略构成.在GAIL 的训练过程中,策略模型在更新的过程中会朝着更容易欺骗鉴别器模态策略的方向更新,导致最终的生成样本分布只能满足部分甚至单一的专家样本分布,因此难以学习到完整的多模态专家策略.多模态的模仿学习方法不再假设专家策略模态是唯一的,而是认为专家策略是由多个模态的子策略构成的.多模态模仿学习方法在这种设定下研究如何更好地完成多模态的模仿学习任务,缓解GAIL 中的模式塌缩问题.
目前,对于GAIL 的模式塌缩问题的解决方法大致分为2 类:一类是有监督的GAIL 方法,该类方法在学习多模态策略时,需要使用专家样本的模态标签信息,例如CGAIL,ACGAIL 等;另一类是无监督的GAIL 方法,此类方法从没有模态标签的专家样本中学习多模态策略,例如VAE-GAIL,InfoGAIL.按照模态标签数据类型的不同,多模态的GAIL 方法可划分为离散模态标签与连续模态标签的多模态模仿学习方法.其中CGAIL,ACGAIL,InfoGAIL 的模态标签均为离散的形式,而VAE-GAIL 推断的模态隐变量为连续的形式.
另外Fei 等人[22]将各个模态定义为不同的技能,在GAIL 模型基础上增加了辅助选择器,提出了Triple-GAIL.在Triple-GAIL 中,辅助选择器根据智能体所处的不同状态,选择适合的技能.
1.4 余弦相似度
余弦相似度(cosine similarity)又称余弦相似性,是一种通过计算2 个向量之间的余弦值来评估两者相似程度的方法.当2 个向量正交时,则称它们线性无关,其余弦相似度为0;当2 个向量平行且同向时,它们的余弦相似度为1.定义在线性空间 R中有限维空间 V 中任意2 个非零向量α,β ∈R.α 和 β的余弦相似度可以定义为
余弦相似度反映了向量之间的相关性,向量之间的余弦值越大,表示2 个向量包含的相似信息越多.在MCS-GAIL 中,将智能体根据不同模态策略分别采集的样本和专家样本输入编码器.编码器根据不同模态的状态-动作对,输出相应的特征向量.对于不同模态的样本,编码器输出的特征向量各不相同.另外,将不同模态的专家样本输入编码器,得到不同模态特征向量的信息也各不相同.在采样样本与专家样本中,相同模态样本的特征向量应该是相似的.使用余弦相似度衡量特征向量的相似度,并将余弦项加入智能体的策略损失中,对策略组进行梯度下降,在强化学习方法的指导下求解不同模态的最优策略.通过计算不同模态特征向量间的余弦相似度,使各个模态的策略以互补的方式学习专家策略.
2 MCS-GAIL
2.1 整体框架
如图2 所示,基于MCS-GAIL 由策略组(policies)、鉴别器(discriminator)和编码器(encoder)构成.策略组和鉴别器延续GAIL 中的结构.其中策略组的输入为智能体所处的状态s,输出为在所处状态下智能体根据策略选择的动作a.鉴别器和编码器的输入均为状态-动作对(s,a).鉴别器的输出为状态-动作对来自专家样本的概率,编码器则根据不同模态的状态-动作对,输出不同的特征向量.在MCS-GAIL 中,策略组中子策略模块的个数与专家策略模态数量相同,每一个子策略模块根据输入的状态与模态标签,输出对应模态的动作.在训练策略组时,MCS-GAIL 以各个子模态采样样本的模态特征与各个专家样本的模态特征计算余弦项,并使用余弦项引导各个子策略学习相应模态的专家策略.

Fig.2 Illustration of MCS-GAIL图2 MCS-GAIL 示意图
在MCS-GAIL 训练开始前,以不同模态间的余弦相似度作为约束,预训练编码器,使编码器可以根据不同模态的专家样本输出不同的模态特征.在MCS-GAIL 训练时,智能体依据策略组与环境进行交互,采集当前策略组的样本.在逆向强化学习过程中,根据智能体采集到的样本与专家样本共同更新鉴别器,提高鉴别器的辨别能力.在强化学习过程中,使用策略损失更新策略组,MCS-GAIL 的策略损失由2部分构成:1)根据编码器输出的样本特征向量计算的余弦项;2)根据鉴别器输出的概率值而计算的优势函数.通过强化学习过程与逆向强化学习过程的交替迭代,智能体利用专家样本中不同模态样本的特征信息以及特征信息间的余弦关系,学习不同模态的专家策略.
2.2 编码器的预训练
为了构建样本的特征向量,编码器将不同模态的样本分布映射到不同的样本特征分布.在GAIL 模型训练结束时,当前策略采样的样本分布会趋近于专家的样本分布.此时,采样样本与专家样本间相同模态的特征向量一一对应.另外,在进行策略开始训练之前,可以使用专家样本对编码器进行预训练,加快策略模型的训练速度,提高训练的稳定性.
如何使用专家样本对编码器进行预训练是一个关键的问题.为了解决该问题,MCS-GAIL 利用不同模态样本特征向量的余弦相似度对编码器进行预训练.2 个向量之间的夹角范围为[0,π],2 个向量的余弦相似度绝对值的范围为[0,1].在向量的余弦相似度关系中,当2 个向量正交时,两者包含的相似信息最少;而当2 个向量平行时,两者包含的相似信息最多.在专家样本的余弦相似度关系中,相同模态专家样本的特征向量应该是相似甚至相同的,所以相同模态专家样本的特征向量应该是平行同向的,故2 个特征向量之间余弦相似度值应该为1,不同模态专家样本之间的特征向量应该是不同的,所以不同模态专家样本的特征向量应该是正交的,故余弦相似度值应该为0.综合上述信息,编码器应该使相同模态样本的特征向量平行,即相同模态样本特征向量间的余弦相似度值为1.同样,编码器应该使得不同模态样本间的特征向量正交,即不同模态样本特征向量间的余弦值为0.故预训练专家样本特征向量间的余弦相似度关系公式为
其中E表示编码器,cos()表示余弦函数,(s,a)表示专家样本的状态-动作对,状态和动作下标对应不同的模态标签,k表示模态的数量.
对编码器进行预训练如算法1 所示:
2.3 算法分析
与GAIL 相同,MCS-GAIL 仍然是一个最大化鉴别器D和 最小化策略π1:k的极小极大博弈问题.即智能体采集的样本应该与专家样本相似,使鉴别器难以区分专家样本和采样样本.而鉴别器负责抽取专家样本的特征,并利用这些特征区分专家样本与采样样本.策略组与鉴别器在互相博弈中逐渐优化,最终收敛.另外,在MCS-GAIL 方法中,不同模态的策略采集的样本各不相同,这是由于编码器构建的余弦项对策略组的约束.综上所述,MCS-GAIL 方法进行极小极大博弈的公式为
其中,k表示策略组中不同模态策略的数量,λ 和 μ为余弦相似度关系的系数;E表示编码器,用于提取k个模态策略采集样本的特征向量;π(a|s)表示智能体位于状态为s时,根据策略 π选择的动作为a;πi(a|s)和πj(a|s)分别表示模态i和模态j选择动作的策略;pei表示模态i专家样本的分布.
在MCS-GAIL 的强化学习过程中,策略组以余弦项作为约束,学习对应模态的专家策略,使鉴别器难以区分采样样本与专家样本.在MCS-GAIL 的逆向强化学习过程中,通过提升鉴别器D(s,π1:k(a|s))的分类能力,使鉴别器可以最大限度地将正确标签分配给采样样本和专家样本.MCS-GAIL 优化鉴别器D与策略π1:k的公式分别为
在MCS-GAIL 中,策略组在余弦项的约束下,与鉴别器进行极小极大博弈,最终达到纳什均衡.此时pπi与pei基本重叠.当策略 πi的样本分布与pei完全重叠时,鉴别器也会收敛到最优值D*(s,a),即鉴别器D将会在pe=(pπ1+pπ2+…+pπk)/k处取得最优值.为了简化推导过程,本文后续部分将pπ1+pπ2+…+pπk记为pπ.
引理 1.对于策略π1:k,最优鉴别器D*(s,a)为
证明.在给定策略组π1,π2,…,πk联合构成分布的情况下,通过最大化MCS-GAIL 的目标函数,对鉴别器D进行更新.MCS-GAIL 目标函数为
计算鉴别器函数关于(s,a)的偏导数,并令该项为0,整理得到
进一步整理,目标函数LMCS-GAIL(π1:k,D)在点D*(s,a)=pe/(pe+pπ/k)处取得最优值D*(s,a)= 1/2,此时pe=pπ/k.
证毕.
结合引理1,将式(7)代入式(5),得到
当鉴别器为最优值时,策略损失中的余弦项取得最小值,将式(10)中后2 项,即余弦项记作 δ.并将式(10)进一步整理得到式(11):
其中fJS表示JS 散度,表示策略组的联合分布pπ/k.从式(11)可知,MCS-GAIL 的目标函数主要由2 部分构成:1)策略组的联合样本分布与专家样本分布间的JS 散度;2)专家样本特征向量与采样样本特征向量间余弦关系的约束项.
定理1.当且仅当每个模态策略的样本分布与对应模态的专家样本分布重合时,MCS-GAIL 的目标函数取得的最优值=-2log2+δ.
证明.由引理1 可知,当策略组的分布与专家样本分布相等时,即pe=pπ/k,鉴别器的目标函数取得的最优值D*(s,a)=1/2.由JS 散度的数学性质可知,式(11)中,专家样本分布与策略采集的样本分布之间的JS 散度是非负的.而且当策略组的分布满足pe=pπ/k时,JS 散度达到最小值0;当策略组样本分布逐渐趋近于专家样本的分布,满足引理1 时,JS 散度达到最小值,余弦项也到达最小值.此时MCSGAIL 的目标函数取得的最优值=-2log2+δ.
证毕.
另外,在基于单模态设定的GAIL 中,当初始策略的样本分布与专家样本分布完全没有重叠或重叠部分可以忽略不计时,策略的样本分布与专家样本分布之间的JS 散度是一个常数.此时,出现梯度消失问题,策略模型难以更新.而在MCS-GAIL 中,即使初始的策略组的样本分布与专家样本分布完全没有重叠,MCS-GAIL 仍然可以学习到最优策略.假设在某个时刻策略组样本分布与专家样本分布完全没有重叠,2 个分布的JS 散度值为2log2.在这种情况下,虽然难以通过策略组的损失项更新策略组,但仍然可以通过余弦项更新策略组.因此,在MCS-GAIL 的策略更新过程中不会出现梯度消失问题.
如式(10)(11)所示,MCS-GAIL 方法仍然是一个极小极大博弈问题,其目标函数L(π1:k,D)是一个凸函数.根据Sion 极小极大定理[23],凸函数的最大值一定包含在其上确界的次导数中,即如果任意α,fα(x)对于x都是凸函数,并有f(x)=fα(x),则∂fβ(x)∈∂f,β=argsupfα(x).设pe和是2个线性拓扑空间的非空凸紧集 ,有L(π1:k,D)≥L(π1:k,D).在给定最优鉴别器D和 1 组策略组的情况下,对策略组进行梯度下降,更新当前的策略组,优化当前策略分布pπ1:k.在优化过程中supL(π1:k,D)是凸的,具有唯一的全局最优,因此pπ1:k在够小的更新下可以收敛到pe.
3 实 验
本节主要介绍MCS-GAIL 的实验部分.为了更全面地比较各个模式塌缩方法的性能,MCS-GAIL 既选取了较为简单的离散状态-动作空间的格子世界任务作为实验环境,又选取了较为复杂的连续状态-动作空间的MuJoCo[24]平台作为实验环境.
MCS-GAIL 基于已知模态标签的设定进行模式塌缩问题的研究,选取2 种已知模态标签的多模态模仿学习方法与MCS-GAIL 进行对比.
3.1 格子世界环境
3.1.1 实验环境
如图3 所示,MCS-GAIL 使用状态空间为7×7的格子世界环境,格子世界的状态数值范围为从左下角开始向右依次递增,分别为{0,1,…,48},动作空间为{上,下,左,右}.图3 中的圆形为智能体;白色格子为智能体可到达的状态;黑色格子为智能体不可到达的状态,即放置了障碍物.

Fig.3 Illustration of grid world environment图3 格子世界环境示意图
智能体从左上角格子出发,到达右下角五角星格子时,视为完成任务,当前情节结束.若智能体与障碍物碰撞,则会停留在原地,并获得负奖赏.在这种设定下,智能体应该尽量避免与障碍物发生碰撞,并以尽可能短的路径到达终点.
3.1.2 专家数据
由于格子世界任务较为简单,故使用经典的强化学习方法Q-Learning 训练专家策略,并使用专家策略采集专家样本.在格子世界的模式塌缩问题中,不同模态策略完成任务的轨迹各不相同.在此次实验中,设置6 种不同模态的专家策略,6 种策略完成任务的路径各不相同.
专家样本中不同模态策略的状态轨迹如图4 所示.其中黑色格子为障碍物,箭头表示采样轨迹中智能体移动的轨迹.

Fig.4 Trajectories diagram of expert strategy states in different modals图4 不同模态专家策略状态轨迹图
3.1.3 实验结果
在格子世界任务中,各个方法均使用深度神经网络对鉴别器进行建模,鉴别器均包含一层全连接层和一层输出层.全连接层由32 个神经元组成,并使用tanh 函数作为激活函数,同时使用RMSprop 优化算法更新鉴别器.由于格子世界环境较为简单,故使用经典的Q-Learning 方法学习多模态策略.其中,价值函数的维度为6,49,4,这3 个维度分别表示模态数量、状态维度以及动作维度,并使用ε-greedy方式更新价值函数.在训练结束后,使用策略分别对环境进行采样,评估各个模态方法采集的样本状态轨迹与专家样本状态轨迹之间的差异.在格子世界环境中设置式(5)中 λ 和 μ参数的值均为0.8,另外表1 给出了格子世界任务中3 个多模态方法的超参数.

Table 1 Hyperparameters of Methods in Grid World Task表1 格子世界任务中方法的超参数
1)GAIL 策略的状态轨迹如图5 所示,GAIL 并没有考虑专家样本的多样性,而是将多模态专家样本学习到单个策略中.为了更清楚地展示GAIL 中的模式塌缩问题,使用6 个随机种子对GAIL 进行训练.从图5 中可以看出,GAIL 虽然可以完成格子世界任务,但进行6 次模型训练后,仅仅从6 种模态专家样本中学习到3 种模态的专家策略和1 种混合专家路径的策略.综上所述,在1 次训练中,GAIL 没有考虑专家样本中的多模态特性,只能学习到1 个模态的专家策略或1 个混合专家路径的策略;在6 倍于模式塌缩模仿学习方法训练量的情况下,GAIL 的策略也难以覆盖全部的模态策略.
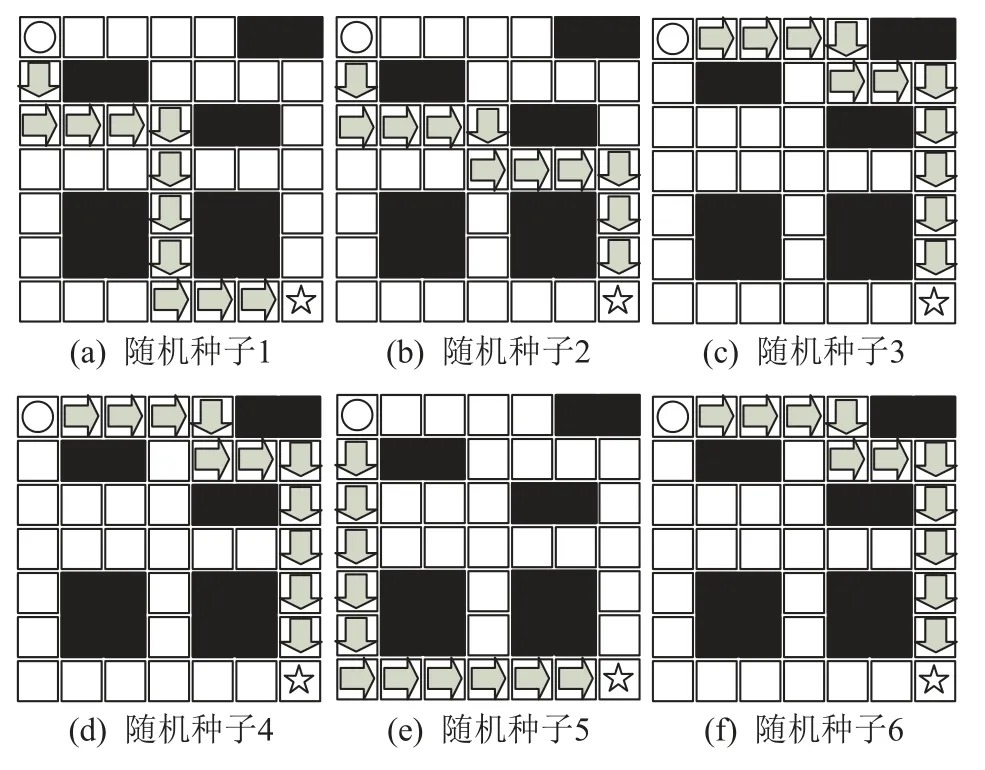
Fig.5 GAIL policy sampling state trajectory diagram图5 GAIL 的策略采样的状态轨迹图
2)CGAIL 策略采样的状态轨迹如图6 所示,CGAIL 将模态标签加入策略中,学习多种模态的专家策略.从图6 中可以看出,CGAIL 可以学习到大部分模态的专家策略.但与专家状态轨迹相比,CGAIL并没有学习到所有模态的专家策略.CGAIL 中5 个模态的策略采样状态轨迹与图4 中专家的状态轨迹相同.而模态4 的策略采样的状态轨迹为混合专家状态轨迹.由此可见,CGAIL 在解决具有多模态的模仿学习问题中仍有缺陷.
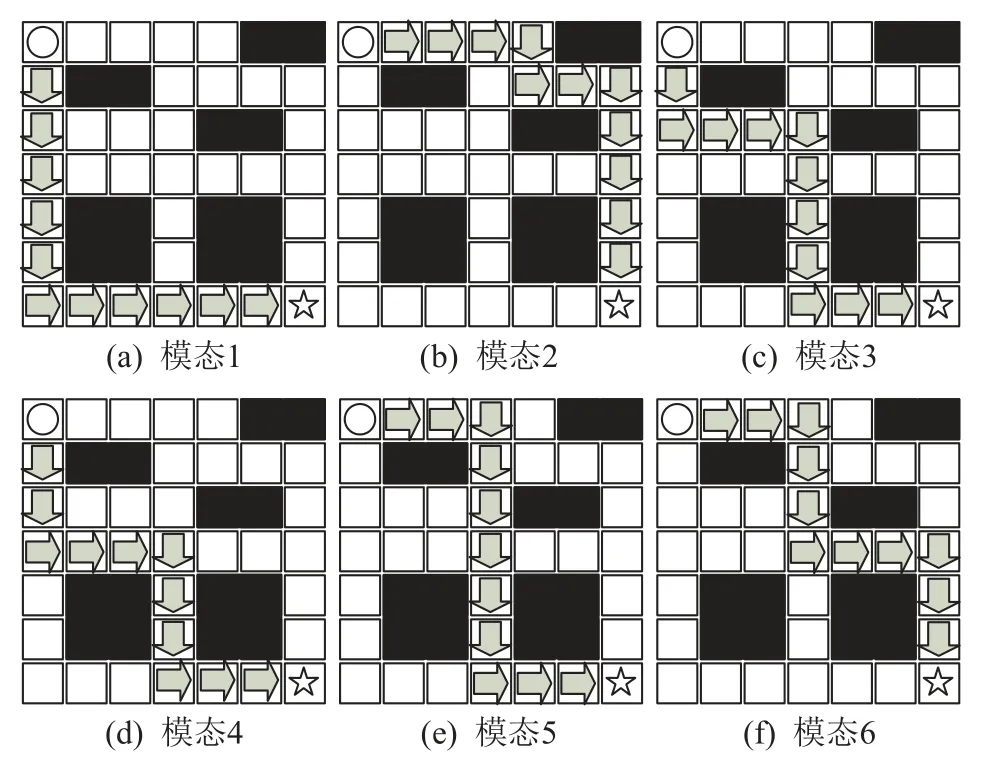
Fig.6 CGAIL policy sampling state trajectory diagram图6 CGAIL 的策略采样状态轨迹图
3)图7 为ACGAIL 的策略采样状态轨迹,ACGAIL虽然在CGAIL 的基础上增加了辅助分类器,将专家样本的模态特征加入模型训练,但是ACGAIL 的策略与鉴别器共享参数,导致在训练过程中神经网络的更新会相互影响.与CGAIL 相比,ACGAIL 虽然也只学习到5 种模态的专家策略,但是ACGAIL 学习到的重复的策略状态轨迹与专家模态6 的轨迹相同.
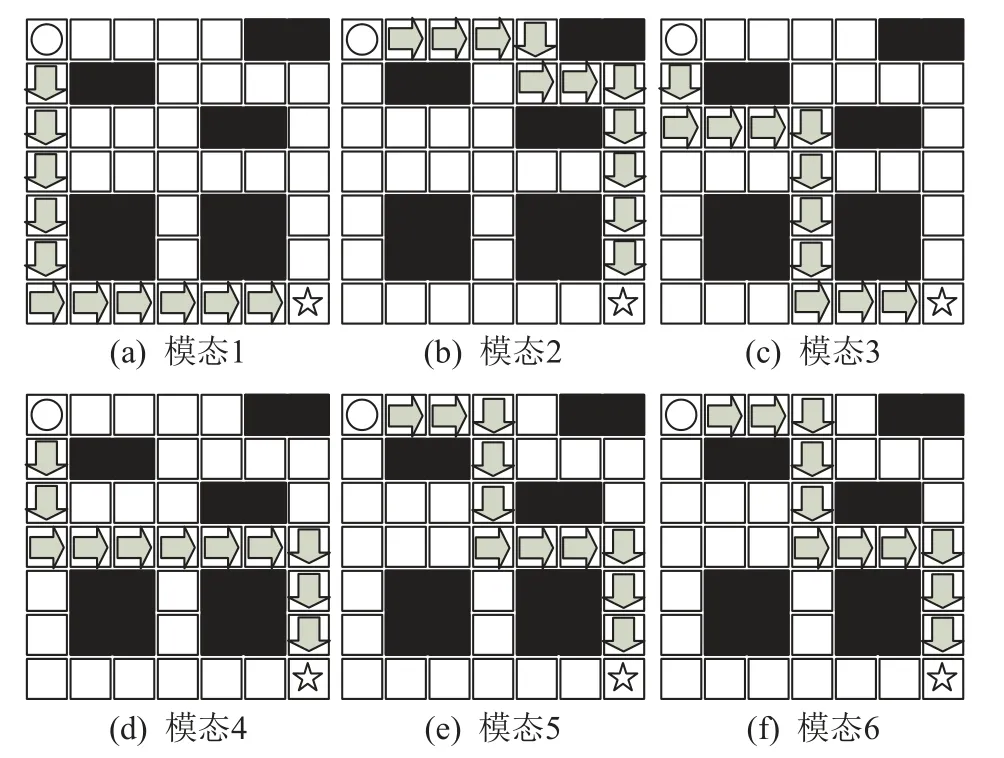
Fig.7 ACGAIL policy sampling state trajectory diagram图7 ACGAIL 的策略采样状态轨迹图
4)MCS-GAIL 在格子世界中的策略采样状态轨迹如图8 所示,MCS-GAIL 将各个模态特征向量间的余弦相似度关系加入模型训练后,各个模态策略的状态轨迹与专家的状态轨迹完全一致.由此可见,与其他3 种方法相比,MCS-GAIL 可以准确学习到所有模态的专家策略,很好地完成多模态模仿学习任务.

Fig.8 MCS-GAIL policy sampling state trajectory diagram图8 MCS-GAIL 策略采样状态轨迹图
3.2 MuJoCo 环境
Gym 是人工智能公司OpenAI 针对强化学习方法开发的仿真平台,涵盖了丰富的实验环境,例如经典控制游戏、Box2D 环境、Atari 游戏环境以及MuJoCo环境等.
3.2.1 实验环境
为了探究多模态模仿学习方法在复杂连续状态-动作空间环境中的性能,使用MuJoCo 环境中的3 个环境区分机器人速度的任务(Hopper-v2,HalfCheetahv2,Walker2d-v2).这3 个实验环境的状态空间和动作空间均为连续空间,其具体介绍如表2 所示.
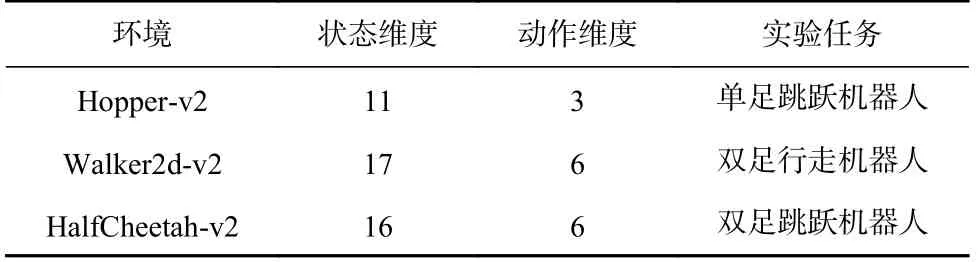
Table 2 Introduction for MuJoCo Experimental Environment表2 MuJoCo 实验环境介绍
CGAIL,ACGAIL,MCS-GAIL 在MuJoCo 环境训练过程中,对各个模态策略进行若干个情节的评估,得到平均每情节回报,简称平均回报.在训练结束后,将GAIL 加入评估,比较在MuJoCo 环境中4 种方法的回报误差率[25].
3.2.2 专家样本数据集
在MuJoCo 环境中,使用柔性行动者-评论家 (soft actor-critic,SAC)算法训练专家策略[26].为了区分不同模态,在每个实验环境下均训练2 个不同速度的专家策略,并使用训练后的专家策略对环境进行采样,得到专家样本数据集.每个数据集包含1 500 个状态-动作对序列,每个序列包含1 000 个状态-动作对.
在MuJoCo 环境中,智能体的速度与平均回报的大小成正比.速度较快的状态-动作对与速度较慢的状态-动作对相比,具有较大的奖赏,所以在进行模型评估时,速度较快的专家策略的平均回报也比速度较慢的专家策略的大.因此,可以将策略的平均回报作为模态的区分准则.在MuJoCo 各个环境的数据集中,不同模态专家样本的平均回报如表3 所示.
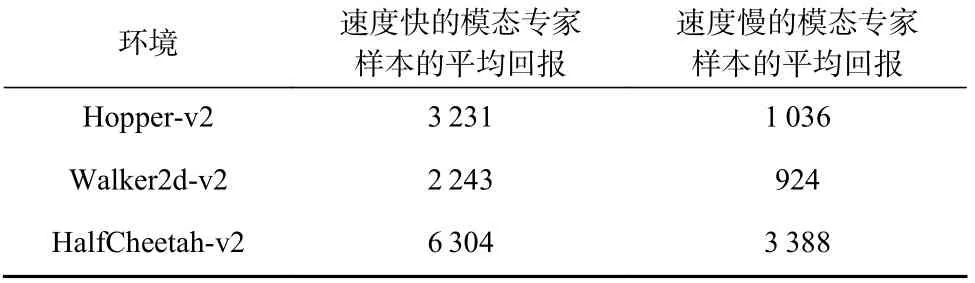
Table 3 Average Returns for Different Modals in the MuJoCo Expert Demonstrations表3 MuJoCo 专家样本中不同模态的平均回报
3.2.3 评价标准
在模仿学习方法中,一般通过比较专家策略平均回报与模仿学习方法策略平均回报之间的差异,衡量方法的性能.为了准确衡量不同方法的性能,首先计算策略与专家策略之间期望回报的误差,然后将该误差与专家策略期望回报之间的比率作为评价标准,称为回报误差率.回报误差率公式为
其中k为模态的数量,(c)表示模态标签为c的策略评估的平均回报,(c)表示模态c的专家样本的平均回报,p(c)表示模态c出现的概率分布.
3.2.4 实验结果
在策略的训练过程中,每次强化学习迭代后,将策略进行10 次评估的平均回报作为当前策略的回报.另外,在评价最终模型的回报误差率时,将GAIL加入对比,评估GAIL 中的模态丢失情况.
在MuJoCo 实验中,各个方法均使用深度神经网络对策略、鉴别器以及编码器进行建模.鉴别器、策略以及编码器均使用3 层全连接层和1 层输出层,全连接层由100 个神经元组成,并使用tanh 函数作为激活函数,同时使用RMSprop 优化算法更新策略模型,但是在更新编码器和鉴别器时使用Adam 优化算法;在强化学习过程中策略的更新均使用信赖域策略优化[27](trust region policy optimization,TRPO)算法.MuJoCo 环境中设置式(5)中 λ 和 μ参数的值均为0.8,另外表4 给出了MuJoCo 任务中3 个多模态方法的超参数.

Table 4 Hyperparameters of Methods in MuJoCo Task表4 MuJoCo 任务中方法的超参数
图9 给出了MCS-GAIL 与其他基线模型在3 个MuJoCo 实验环境训练过程中所获得的平均回报.其中实线表示在迭代过程中评估的平均回报,虚线表示专家样本的平均回报.为了区分不同的模态,使用不同颜色表示不同模态策略的平均回报.图9(a)~(c)为MCS-GAIL 在训练过程中的平均回报,图9(d)~(f)为CGAIL 在训练过程中的平均回报,图9(g)~(i)为ACGAIL 在训练过程中的平均回报.

Fig.9 Average returns during the training of each method in the MuJoCo environment图9 MuJoCo 环境中各个方法训练过程中的平均回报
根据图9 可以看出MCS-GAIL 在多模态任务中的表现明显优于CGAIL 和ACGAIL,具体分析有4 点.
1)MCS-GAIL 中2 个模态策略的分离程度远远大于基线方法,MCS-GAIL 中2 个模态策略的平均回报分离程度明显超越了CGAIL 和ACGAIL.这是因为余弦项对不同模态策略的约束,提高了不同模态策略的区分程度,避免策略学习其他模态的专家样本信息.
2)由于余弦项对同模态专家样本与当前采样样本的约束,在策略组的迭代过程中,MCS-GAIL 策略朝着对应模态专家策略的方向更新,增加了MCS-GAIL策略与对应专家模态策略的近似程度.从图9 中可以看出,MCS-GAIL 的策略与同模态专家策略的平均回报的趋近程度远远优于其余2 种方法.
3)在训练过程中,3 种方法平均回报的值都存在一定的波动,但是MCS-GAIL 的波动相对较小.平均回报产生波动的原因有2 个方面:1)强化学习训练过程中,策略参数的更新,即使策略参数变化很小,也会导致整个情节的状态-动作对产生很大的改变.2)生成对抗框架的不稳定性,这是由于训练最优鉴别器与最小化策略之间相互矛盾所致[28].MCS-GAIL 在余弦项的约束下,大大减小了在训练过程中平均回报的波动程度.
4)在强化学习过程中,随机种子不同的情况下,MCS-GAIL 策略的方差远小于其余2 种方法.可见,相比于其他2 种方法,MCS-GAIL 具有更好的鲁棒性.
综上所述,在MuJoCo 实验平台下,MCS-GAIL在训练过程中更加平稳、高效,充分表明了该方法在解决多模态模仿学习问题过程中的优越性.
图10 展示了在HalfCheetah-v2 环境的训练过程中,MCS-GAIL 采样样本与专家样本特征向量间的余弦损失.从图10(a)可以看出,MCS-GAIL 采样样本与同模态专家样本特征间的余弦损失随着迭代次数的增加而增大.当同模态策略越接近时,采样样本特征间向量的余弦损失越大.从图10(b)中可以看出MCSGAIL 的样本与不同模态专家样本间的特征值随着迭代次数的增加而减小.当不同模态策略分离程度越大时,采样样本间特征向量的余弦损失越小.综上所述,特征向量间的余弦损失可以准确地反映模态间关系,并以此为依据训练策略,使其更为接近专家策略.
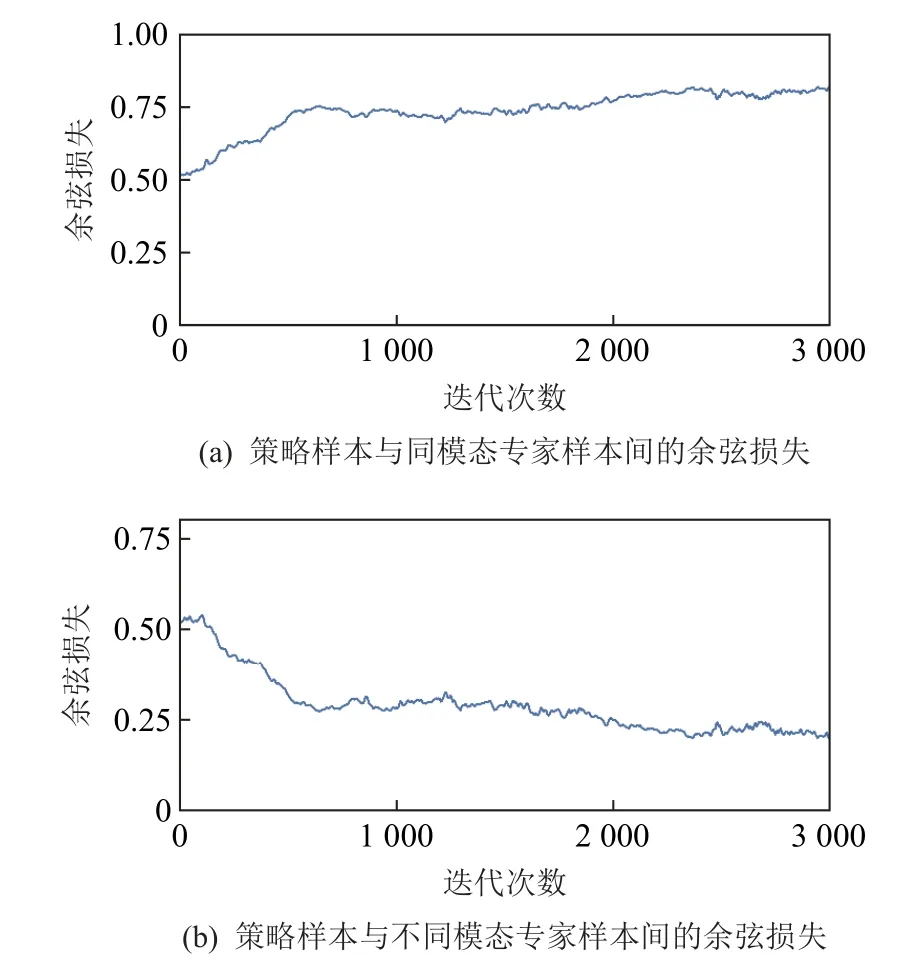
Fig.10 Cosine loss during training in the HalfCheetah-v2 environment图10 HalfCheetah-v2 环境中训练过程中的余弦损失
在MCS-GAIL 的训练初期,各个模态策略的样本分布与对应模态的专家样本分布相距较远,余弦项也不符合预期.在训练中期,利用式(11)的最终结果作为损失函数对策略组进行梯度下降,策略损失随着神经的更新而减小,同时余弦损失也在减小.在训练末期,各个模态策略的样本分布接近对应模态专家样本的分布,余弦项的值也逐渐接近最小值.在训练结束时,各个模态策略的样本分布与对应模态的专家样本分布完全重合,余弦项也取得最小值.
图11 展示了在HalfCheetah-v2 训练过程中,鉴别器对采样样本和专家样本的分类正确率.从图11 可以看出,在训练的开始阶段,鉴别器判别样本的正确率会急剧上升到1.0 附近.这是由于在训练的开始阶段,MCS-GAIL 的采样样本与专家样本差距较大,两者样本特征的差距同样很大,鉴别器很容易区分专家样本和MCS-GAIL 的样本.随着训练次数的逐渐增加,MCS-GAIL 策略逐渐逼近专家策略.此时MCSGAIL 的样本分布与专家样本分布的重合程度越来越高,鉴别器难以区分样本是来自于MCS-GAIL 还是专家样本.在训练的最后阶段,鉴别器已经完全无法区分样本是否为专家样本,即可以认为该策略的决策与专家行为一致.

Fig.11 Classification accuracy of discriminator during training in HalfCheetah-v2 environment图11 HalfCheetah-v2 环境训练中鉴别器的分类正确率
为了更全面地对多模态模仿学习方法进行比较,3 个多模态方法的时间成本如表5 所示.表5 中数据的单位为每运行10 000 个时间步所花费的秒数.从表5 中可知,由于CGAIL 仅仅使用模态标签对学习多模态数据进行指导,故其在3 个MuJoCo 环境中的时间成本均为最小.而ACGAIL 在CGAIL 的基础上增加了辅助分类器提取模态特征,因此时间成本有所增加.MCS-GAIL 相对ACGAIL 来说不仅增加了组件提取模态特征,而且增加了模态特征余弦关系的运算.因此与ACGAIL 相比,MCS-GAIL 在3 个MuJoCo环境中的时间成本有略微地提高.但MCS-GAIL 更侧重于提高多模态模仿学习方法的准确性,以微小的时间成本换取学习多模态专家策略的精度,这表明了MCS-GAIL 具有较高的应用价值.
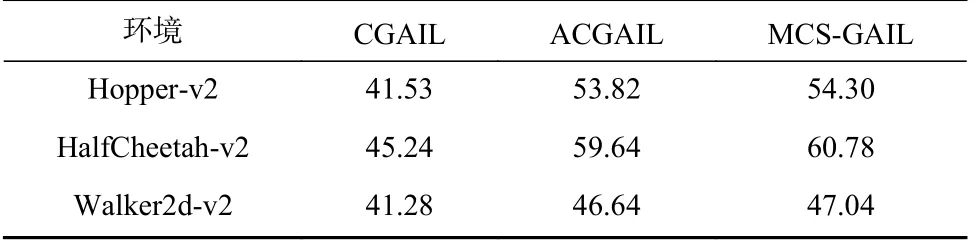
Table 5 Time Cost of Multi-Modal Methods表5 多模态方法的时间成本s
各种方法均使用5 个随机种子对MuJoCo 环境中的3 个任务进行采样,不同多模态模仿学习方法的回报误差率如表6 所示.从表6 中可以看出,在3个环境中,GAIL 在多模态生成对抗模仿学习任务中只能学习到单一模态的策略,导致训练完成后策略的回报误差率比较高;而CGAIL 和ACGAIL 利用专家样本模态信息优化策略,从而大大降低了回报误差率;MCS-GAIL 不仅利用模态信息优化策略,而且在策略的损失函数中加入余弦项,进一步缩小学习策略与专家策略间的差距,提高了学习策略与专家策略的拟合程度.从表6 可以看出,MCS-GAIL 的回报误差率远小于其他3 种方法,表明了MCS-GAIL 方法可以很好地解决模仿学习中的模态塌缩问题,准确地学习到专家策略.
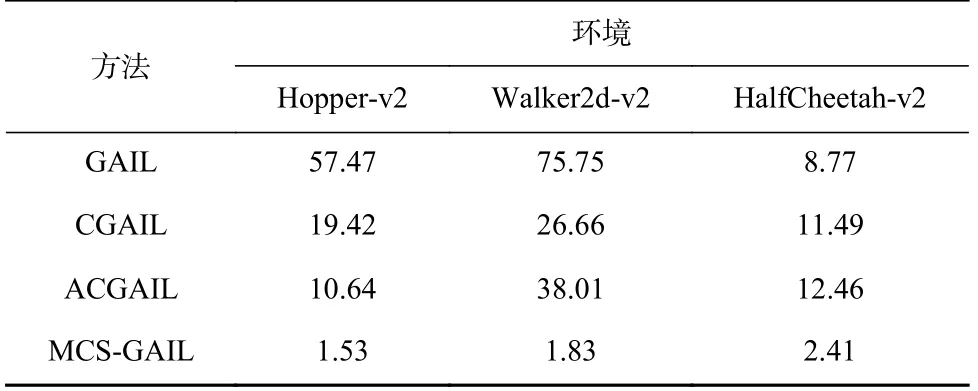
Table 6 Return Error Rates of Different Methods in MuJoCo Environment表6 MuJoCo 环境下不同方法的回报误差率%
4 结 论
本文提出了用于解决模式塌缩问题的多模态模仿学习方法MCS-GAIL.MCS-GAIL 首先在编码器提取专家样本特征向量的同时,对编码器进行预训练;然后将依据余弦关系构建的余弦项加入强化学习的策略损失中,更新策略组.现有的大部分多模态模仿学习方法仅使用模态标签,或者利用模态特征学习专家策略,而没有衡量所学策略与专家策略间的样本分布的趋近程度.与现有多模态对抗模仿学习方法相比,MCS-GAIL 在使用模态标签和模态特征的基础上,使用余弦相似度衡量策略与专家策略间样本分布的关系.策略组在余弦项的约束下模仿专家样本学习专家策略,使策略组可以更准确地学习专家策略.另外,通过理论分析证明了,在假设条件成立的情况下,MCS-GAIL 的收敛性.
在实验方面,MCS-GAIL 使用离散状态-动作空间的格子世界环境和连续状态-动作空间的MuJoCo平台对现有多模态模仿学习方法的性能进行评估.实验结果表明:在格子世界问题中,与现有模式塌缩问题的方法相比,MCS-GAIL 可以准确地学习到多个模态的专家策略.在MuJoCo 环境训练过程中,随着迭代次数的增加,相同模态采样样本的特征向量间的余弦值越来越大,不同模态采样样本的特征向量间的余弦值越来越小.这表明随着迭代次数的增加,训练的策略越来越接近相同模态的专家策略,而远离不同模态的专家策略.在MuJoCo 平台上对4 种多模态模仿学习方法的回报误差率进行比较,MCSGAIL 的回报误差率远远低于其他方法,充分证明了所提方法的可行性、稳定性以及优越性.
作者贡献声明:郝少璞提出整体研究思路、撰写与修改论文;刘全负责论文结构设计指导;徐平安负责方法的整理与部分章节内容的修订;张立华负责部分章节的内容设计和修订;黄志刚负责文章的格式修改、插图设计.

