探寻题根,以变促思
魏燕红


[摘 要]为了以变促思,现以人教版数学教材六年级下册《百分数(二)》单元的变式练习为例,通过“条件不变,问题改变”“变化条件,问题不变”“互换问题和条件”“题型变化,解法不变”“条件和问题不变,解法改变”等策略,设计相应的变式练习,使学生真正掌握百分数的知识,提高学生运用百分数知识解决生活实际问题的能力。
[关键词]变式练习;百分数;练习设计
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)09-0005-03
变式练习是指在其他教学条件不变的情况下,变化概念和规则的例证。数学教学中设计变式练习,不仅能减少大量的机械性练习,减轻学生的学习负担,还能让学生的作业体现时代气息,使学生真正理解与掌握所学的数学知识。虽然数学题目千变万化,但是基本概念、基本公式和基本例题这“三大基石”始终保持不变。变式练习能帮助学生在变与不变中迁移数学思想方法,实现举一反三的目标。
一、变式练习在数学教学中的意义
(一)能帮助学生灵活运用数学知识
数学课本中,每节课都有一定量的课后练习和单元练习,旨在让学生通过练习巩固本节课所学的知识和技能。变式练习基于数学课本的练习进行改编和再创造,既可以帮助学困生通过练习掌握数学知识和解题方法,有利于他们后续的数学学习,又能让学优生主动思考、归纳解题方法,达到做一题通一类的效果。
(二)能幫助学生掌握数学思想方法
数学课本中的练习通常都是呈现单一的知识点,不利于学生综合运用数学知识解决问题。因此,教师需要精心设计变式练习,将多个数学知识点融入同一个题组中,并渗透相应的数学思想方法,帮助学生感受到数学学习的价值。
(三)能提高学生的数学思维品质
思维品质是评价和衡量学生思维含金量的重要标志。学生通过完成变式练习,可以从不同的角度思考问题,培养思维的发散性和敏捷性;也可以对同一个题组中的题目进行一题多解,培养思维的深刻性和抽象性;还可以验证自己的解题过程和答案是否正确,培养思维的严谨性和批判性。
二、变式练习在数学教学中的应用
在作业中,教师大量使用与设计变式练习,能帮助学生更好地理解数学概念,掌握数学知识和技能,发展学生的数学核心素养。
(一)条件不变,问题改变
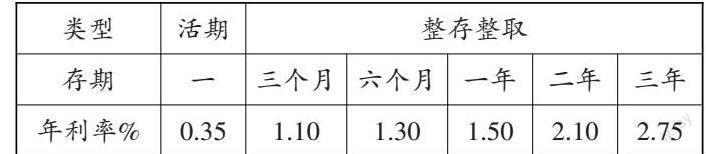
每一道数学题都是由情境、条件和问题组成的,有的题目还包括多个小问题,从不同角度将相关的多个知识点融合在一起,促使学生灵活地运用所学的数学知识解决问题。教师可以对数学课本中的例题和习题进行适当改编,促进学生对问题的深入思考。例如,教学人教版数学教材六年级上册第二单元“利率”中的例题时,教师保留例题中的条件,从不同角度改变例题的问题,促进学生了解储蓄的意义,理解本金、利息、利率的定义以及三者之间的数量关系。
王奶奶把5000元按整存整取存入银行,存二年定期,年利率为2.10%。
(1)到期时连本带息取出,王奶奶可以取出多少钱?
(2)存一年后连本带息取出,王奶奶可以取出多少钱?
(3)王奶奶存二年定期,约定转存,存三年后连本带息取出,王奶奶可以取出多少钱?
(4)王奶奶存二年定期,约定转存,存四年后连本带息取出,王奶奶可以取出多少钱?
储蓄中的利率是百分数在生活中的应用。这样设计变式练习,既能帮助学生养成勤俭节约的好习惯,又可以促进学生了解相关的金融知识,从小培养学生的理财意识。在解决利率问题时,学生需要理解利率的意义,了解银行储蓄的规则。只有这样,才能更好地利用百分数的知识解决储蓄问题,丰富学生的储蓄经验。
(二)变化条件,问题不变
设计变式练习时,可以适当改变题目中的条件,这样就会改变思考过程、解题过程和解题结果。例如,教学人教版数学教材六年级上册第二单元“促销问题”中的例题时,教师保留例题的问题不变,通过变化例题中的条件,促进学生对生活中不同的促销方式有更加深刻的认识。
[课本原题]
某品牌的裙子搞促销活动,在A商场打五五折促销,在B商场按“每满100元减50元”销售。妈妈要买一条该品牌标价230元的裙子。
(1)在A、B两个商场买,各应付多少钱?
(2)选择哪个商场购买更省钱?
[变式练习]
变式1:某品牌的裙子搞促销活动,在A商场打六五折促销,在B商场按“每满200元减50元”销售。妈妈要买一条该品牌标价230元的裙子。
(1)在A、B两个商场买,各应付多少钱?
(2)选择哪个商场购买更省钱?
变式2:某品牌的裙子搞促销活动,在A商场打五五折促销,在B商场按“每满100元减50元”销售。妈妈要买两条该品牌标价230元的裙子。
(1)在A、B两个商场买,各应付多少钱?
(2)选择哪个商场购买更省钱?
变式3:某品牌的裙子搞促销活动,在A商场打七折促销,VIP再享八折;在B商场按“满100元减50元”销售。妈妈办理了该品牌的VIP,要买两条该品牌标价230元的裙子。
(1)在A、B两个商场买,各应付多少钱?
(2)选择哪个商场购买更省钱?
在现实生活中,商场促销有很多不同的方式,如七折促销、现价优惠一成、原价九折、VIP再享八折、买五送二等。因此,在解决促销问题时,要先理解促销方式所表示的具体含义,再把生活中的促销问题转变成数学问题来解决。变式练习是课本原题的升级版,其中的促销方式更加多样化,学生可以通过计算应付的钱或者打了几折来比较在哪个商场购买更省钱,有效提高了学生解决问题的能力。
(三)互换问题和条件
在设计变式练习时,教师可以互换题目中的问题和条件,让学生深入思考。这样学生在解题过程中就要调整原来的思路,以得到正确的结果。教师也可以引导学生尝试互换题目中的问题和条件,这样不仅能让题目更加多样化,还能提高学生思维的敏捷性。例如,人教版数学教材六年级上册第二单元“折扣”中的“做一做”,教材从学生已有的知识经验出发,选择学生熟悉的生活素材,提取有关折扣的数学问题,以唤醒学生的生活经验,激发学生自主解决问题的欲望。
折扣是商品经济中经常使用的一个概念,是百分数问题在生活中的特殊应用。学生在解答有关折扣的问题时,要先弄清楚六五折、七折等折扣表示的含义,再把生活中的实际问题转变成百分数问题,最后根据“原价×折扣=现价”这一数量关系解决问题。课本中的原题是以图片方式呈现具体实物,出示原价和折扣,要求学生利用“原价×折扣=现价”这一数量关系计算现价;变式练习则以表格方式出示实物名称,要求学生利用原价、折扣和现价之间的关系计算出其中的一项,这就需要学生把原来的数量关系进行转化,即“现价÷折扣=原价”“现价÷原价=折扣”,以更加灵活地运用数量关系解决生活实际问题。
(四)题型变化,解法不变
设计变式练习时,教师可以改变题目的情境和内容,但是解题方法保持不变,让学生在不同的题目中找到相同的解题方法。例如,人教版数学教材六年级下册《百分数(二)》,这个单元安排学生解决有关折扣、税率、利率和促销等与百分数有关的生活实际问题,虽然这是百分数在不同领域的应用,但都涉及百分数的数量关系。
[课本原题]
(1)爸爸给小雨买了一辆自行车,原价280元,现在打八五折出售。买这辆自行车用了多少钱?
(2)一个电水壶原价160元,现在打九折出售,与原价相比,便宜了多少钱?
[变式练习]
变式1:
(1)一条裤子原价120元,现在打七五折,这条裤子现价多少元?
(2)王爷爷某月工资中应纳税的部分是3800元,需要按3%的税率缴纳工资薪金个人所得税。这个月他应缴纳工资薪金个人所得税多少元?
(3)张奶奶把8000元按整存整取存入银行,存三年定期,年利率是2.75%。到期后张奶奶可以拿到多少利息?
变式2:
(1)一条裤子原价120元,现在降价20%,这条裤子现价多少元?
(2)去年水稻总产量是1500吨,今年比去年增产一成,今年水稻总产量是多少吨?
(3)张奶奶把8000元按整存整取存入银行,存三年定期,年利率是2.75%。到期后连本带息去除,张奶奶可以取出多少钱?
变式1与课本原题中的第(1)题相似,属于“求A的几分之几是多少”的题型,对应的数量关系是“单位‘1×对应分率=比较量”;变式2与课本原题中的第(2)题相似,属于“已知比一个数多(少)百分之几的数是多少,求这个数”的题型,对应的数量关系是“单位‘1±单位‘1× n% =比较量”或“单位‘1×(单位‘1±n%)=比较量”。这里的变式1和变式2以题组的形式呈现,在学生解答这两组变式题时,教师可以引导学生先比较变式1中题目之间的联系和区别,让学生发现这些题目的数量关系都相同,只是百分数在不同的生活情境中应用;再引导学生比较变式1和变式2的联系与区别,让学生发现这两组变式题的数量关系虽然不同,但都是百分数在生活中的具体应用。
(五)条件和问题不变,解法改变
例如,人教版数学教材六年级下册《百分数(二)》中的一道变式拓展题。
一批笔记本,按50%的利润定价出售,当售出80%后,剩下的笔记本打折出售,结果获得的利润是预定的88%,剩下的笔记本出售时是按定价打了几折?
教师引导学生尝试用不同的方法分析思考,探究出多种解题思路。
[解法1]假设这批笔记本共100本,每本成本1元。
期望总利润:1×50%×100=50(元)
期望的总售价:1×100+50=150(元)
打折后少卖的钱数:50×(1-88%)=6(元)
若全部的笔记本都打折,则少卖的钱数:6÷(1-80%)=30(元)
折扣:1-30÷150=0.8=八折
[解法2]假设这批笔记本共有100本,每本成本是1元,打折部分的百分率是x。
100×(1+50%)×80%+100×(1+50%)×(1-80%)x=100+100×50%×88%
解得:x=80%
……
将题目中的条件和问题保持不变,让学生对同一道题目进行一题多解,利用不同的数量关系探究出不同的解题思路,这样不仅能帮助学生沟通不同方法之间的联系,还可以使学生对这类型的题目有更加深刻的思考和理解。
当然,无论是课本中的練习还是变式练习,都是基于课本中的数学知识,衍生出来的一系列数学问题。这些问题不仅能丰富数学练习资源,还能促进学生更加灵活地运用知识解决生活中的问题,实现学以致用的目的。
[ 参 考 文 献 ]
[1] 夏艳.高效数学课堂的催化剂:变式教学[J].小学教学参考,2020(32):46-47.
[2] 郁雯溪.多视角培养小学生数学解题能力的策略[J].基础教育研究,2021(7):66-67.
(责编 杜 华)

