轻型爬行制孔机器人调姿纠偏分析

曹玉文，刘 荣，张玉枫，徐 明，郝盛镔，刘苏阅

（1. 北京航空航天大学，北京 100191；2. 中车青岛四方车辆研究所有限公司，青岛 266000）

飞机是当今流行的交通工具，在国防军事和生产生活中扮演着重要的角色。飞机制造业对国家经济有着重大影响。为了满足国内自主制造飞机的需求，同时为了提高飞机生产的效率，自动化、数字化和柔性化的飞机生产已经成为主流趋势以及实际生产的需要[1]。飞机制孔是其中的关键环节，不仅影响加工效率[2]，还对飞机整体质量有重大影响[3]。国内飞机制孔自动化程度不高，无法满足未来国内飞机制造的要求，因此，研制自动制孔设备具有重大的战略意义[4]。

在国外，飞机自动制孔设备已有成熟的研究与发展，大型设备、机械臂式移动设备和柔性导轨设备均有投入实际生产的案例，但不同设备各有优劣[5–7]。大型制孔设备效率最高，但单独设备加工的部件单一，设备的研制成本高昂，不适合数字化快速生产的需要。移动机械臂式制孔设备运动灵活，制孔范围大，但由于机械臂结构特性，导致其对振动抑制的能力较弱，且加工效率较低。对于柔性导轨制孔设备来说，其结构质量较轻，加工效率比机械臂式设备高，但由于结构约束，对工作表面的曲率有严格要求，安装需要特殊工装。

爬行机器人式制孔设备整体质量轻，在加工时多处于并联刚性状态，可以较好地进行振动抑制，保证制孔质量，机器人安装不需要特殊工装，定位行走依靠机器人自身感知系统，可以保证较高的系统扩展开发能力，因此本研究选择爬行机器人进行制孔操作研究[8–9]。在运动及调姿时，由于机器人脚部吸附在工作表面不能移动，所以此时机器人的整体结构可以看作并联机构，为了能够完成所需的调姿、纠偏等运动，首先需要对机器人进行数学上的分析[10–14]。

1 机器人自由度分析

本研究所分析的机器人如图1 所示，是使用吸盘进行工作表面吸附并进行加工的自动化工业机器人。机器人的整体结构分为内框和外框，内框架为矩形结构，由4 个横梁相固结组成；外框架为单个横梁结构，分布在内框的两侧，两侧的外框可以分别和内框做相对直线运动。

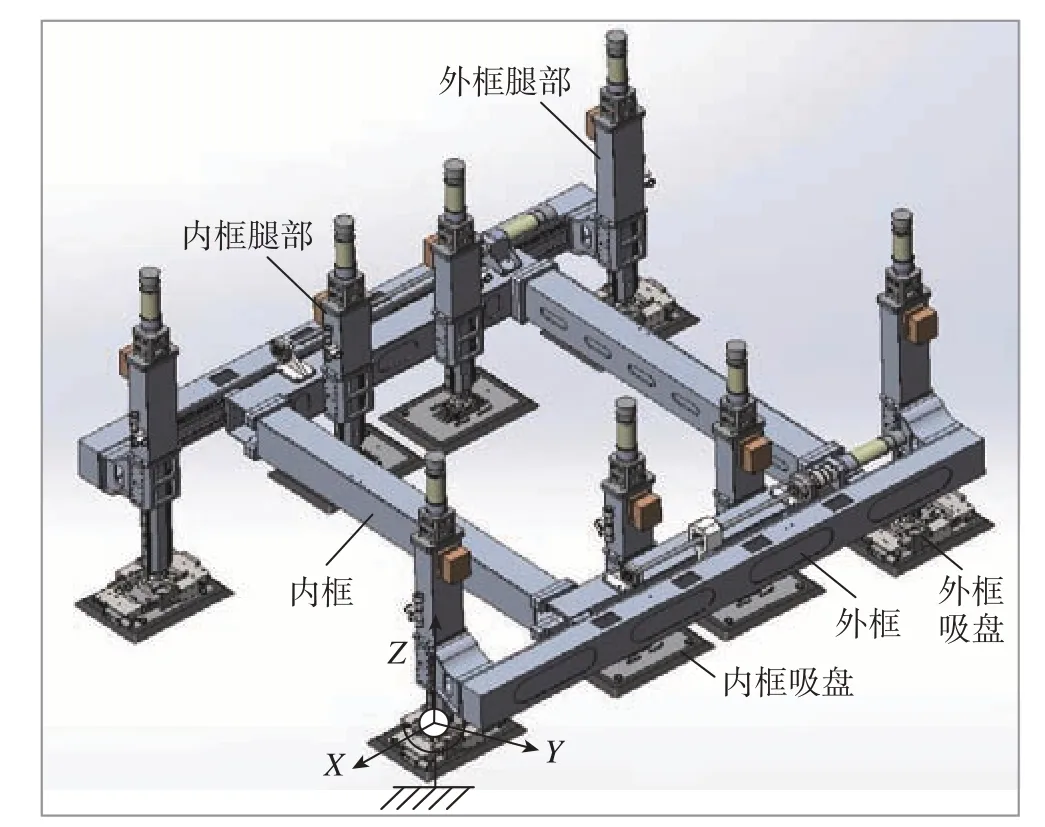
图1 机器人构型简图Fig.1 Robot configuration diagram

机器人依靠脚部的吸盘对工作表面进行吸附，内外框上每个吸盘上均有被动球铰用于吸盘自适应吸附，外框吸盘上有XY方向被动移动的直线导轨，可以单独用钳制器进行自由度限制。内框和外框通过导轨滑块机构相连接。内框上有矩形的末端执行器安装架，安装架具有X和Y方向的自由度，钻孔的钻头通过螺钉与安装架相连。

吸盘和腿部通过球铰相连接。球铰的柱头和腿部的移动件上面均加工有光孔，将光孔对齐后用螺柱和螺母固定。

机器人的8 个腿部仅能垂直于内框进行上下移动，外框可以相对于内框沿导轨进行水平方向移动，所有运动的驱动方式均为滚珠丝杠加配伺服电机。

为了简化计算并深入分析机器人的基本运动原理，本研究的计算都是针对工作面为平面的情况。后文将按照机器人自由度分析、调姿运动正逆解和纠偏运动正逆解的顺序对机器人进行计算和分析。由于外框4 条腿具有相同结构，为了便于计算分析，将选择左前腿（标为0 号）作为运动基准，其余腿的编号如图2 所示，并将此编号用于后续分析计算。

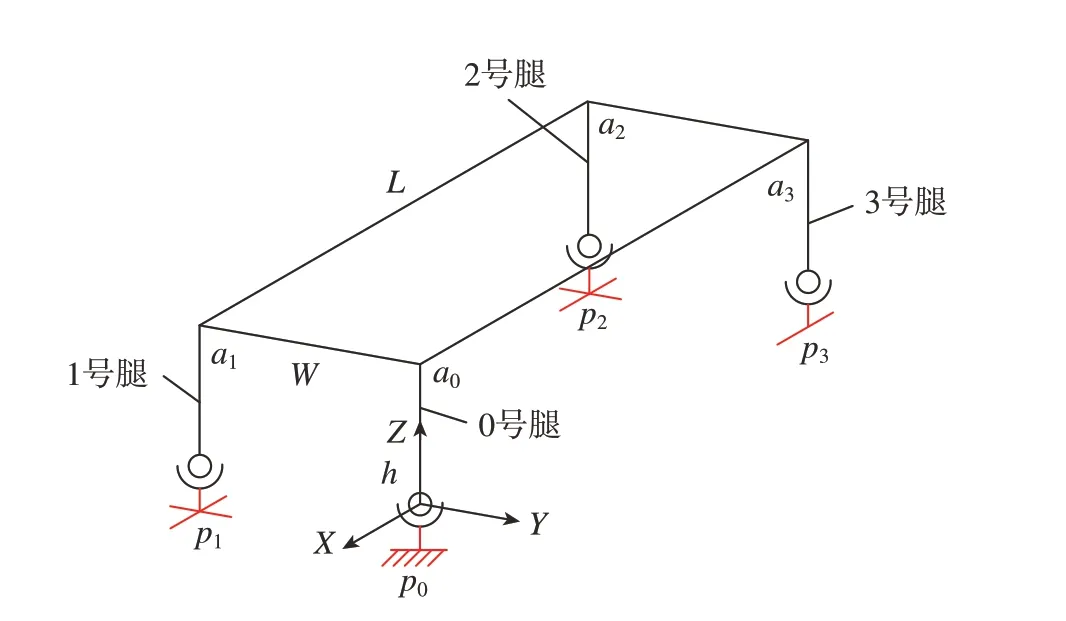
图2 调姿足部锁死方案Fig.2 Posture adjustment and foot lock program

对于调姿与纠偏的过程来说，机器人运动属于并联机器人运动，所以自由度分析应按照并联机器人自由度的分析方法进行。本节对机器人调姿与纠偏的自由度进行分析计算。机器人的4 条腿运动方向均垂直于机器人框架平面，可以看作虚约束。对去除虚约束进一步分析，得到实际情况下机器人的自由度1 为沿Z轴的上下运动。在这种状态下，机器人无法完成调姿或纠偏运动，额外的自由度是必需的。为了满足运动要求，引入吸盘的被动位移。在吸盘的被动位移没有任何限制的情况下，机器人的自由度为3。在不考虑腿部运动的情况下，由于脚部的被动自由度，机器人有沿XY轴位移和绕Z轴旋转的自由度，而在加入4 条腿的运动后，机器人将有6 个自由度。以上结构为机器人的调姿和纠偏运动提供了可能。但其驱动的自由度少于其运动的自由度，所以需要在运动之前对脚部的移动平台进行相应的锁定，限制其自由度，以实现机器人的可控性。

1.1 调姿自由度分析

由于机器人整体自由度多于需要的运动自由度，所以在进行调姿前，需要进行约束，减少机器人的自由度。在调姿的过程中，需要的自由度为绕X轴旋转和绕Y轴旋转的自由度。根据调姿的运动形式，设计机器人依靠4 条腿的伸长缩短，结合机器人脚部的钳制器锁死导轨来实现机器人的自由度约束和姿态调整。具体的锁死方式如图2 所示，0 号腿的X方向运动和Y方向运动锁死，1 号和2 号腿不进行锁死操作，3 号腿只锁死Y方向运动。在该锁死方案下，机器人身体将只进行4 条腿的伸长缩短运动，在此运动方式下，机器人可以进行先绕Y轴旋转，再绕X轴旋转的调姿运动。若需要进行先绕X轴旋转，再绕Y轴旋转的运动方式，需要将1 号腿的锁定状态与3 号腿的锁定状态交换。由此可以得到机器人的自由度dof 为3。其中，2 个自由度属于姿态调整，1 个自由度属于移动运动。

图2 中h为机器人基准高度；L为机器人长度；W为机器人宽度；p0～p3为调姿前腿部末端的位置坐标；a0～a3为调姿前腿部上端的位置坐标。

1.2 纠偏自由度分析

由于机器人整体自由度多于需要的运动自由度，所以在进行纠偏前，同样需要进行约束。根据纠偏运动的模式，设计机器人依靠外框相对运动和机器人足部锁死的方式来实现机器人的自由度约束和角度调整。如图3 所示，机器人0 号腿完全锁死，2 号和3 号腿不进行锁死，1 号腿锁死X方向运动。在纠偏过程中，机器人将只进行两侧外框的相对运动，在此情况下，对机器人整体自由度进行分析，可以得到机器人的自由度dof 为1。其中，该自由度属于绕Z轴旋转。

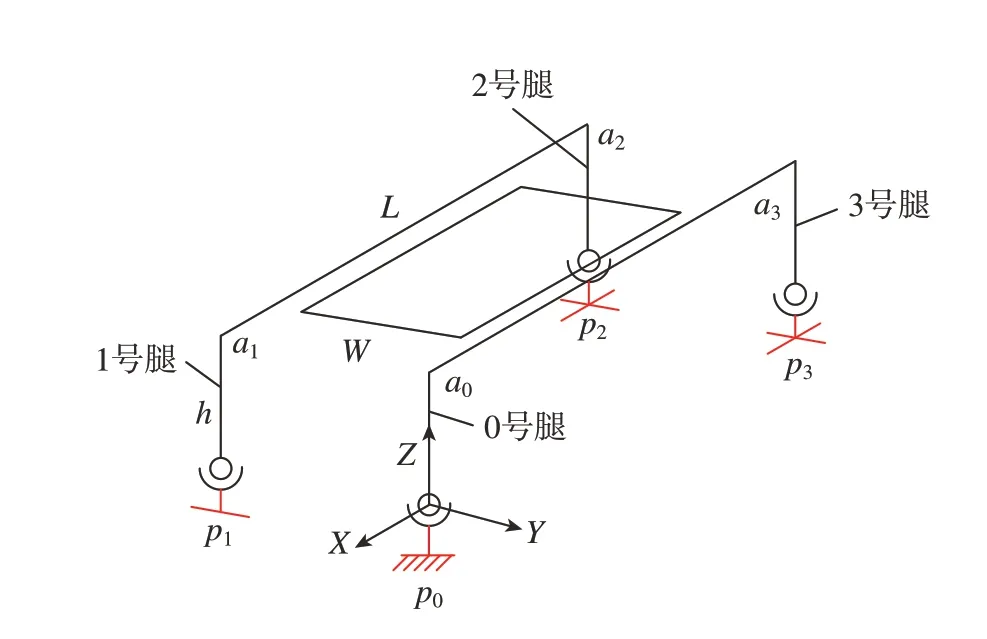
图3 纠偏足部锁死方案Fig.3 Corrective foot lock program

2 调姿运动计算分析

2.1 调姿逆解旋量方程解法

旋量方程法是利用不同腿部作为不同支链，构造从坐标系原点到机器人框架末端的旋量方程[15]，利用不同支链下末端的最终位置相同这一特点，结合机器人的结构特性进行约束，构造方程组，进行未知变量的求解，即可得到腿长和脚部位移等的实际解。实际求解计算可以由Matlab 完成。

该方法中建立的原点坐标系在未调姿机器人身体正下方的中心处，机器人调姿的结构简图如图4 所示。

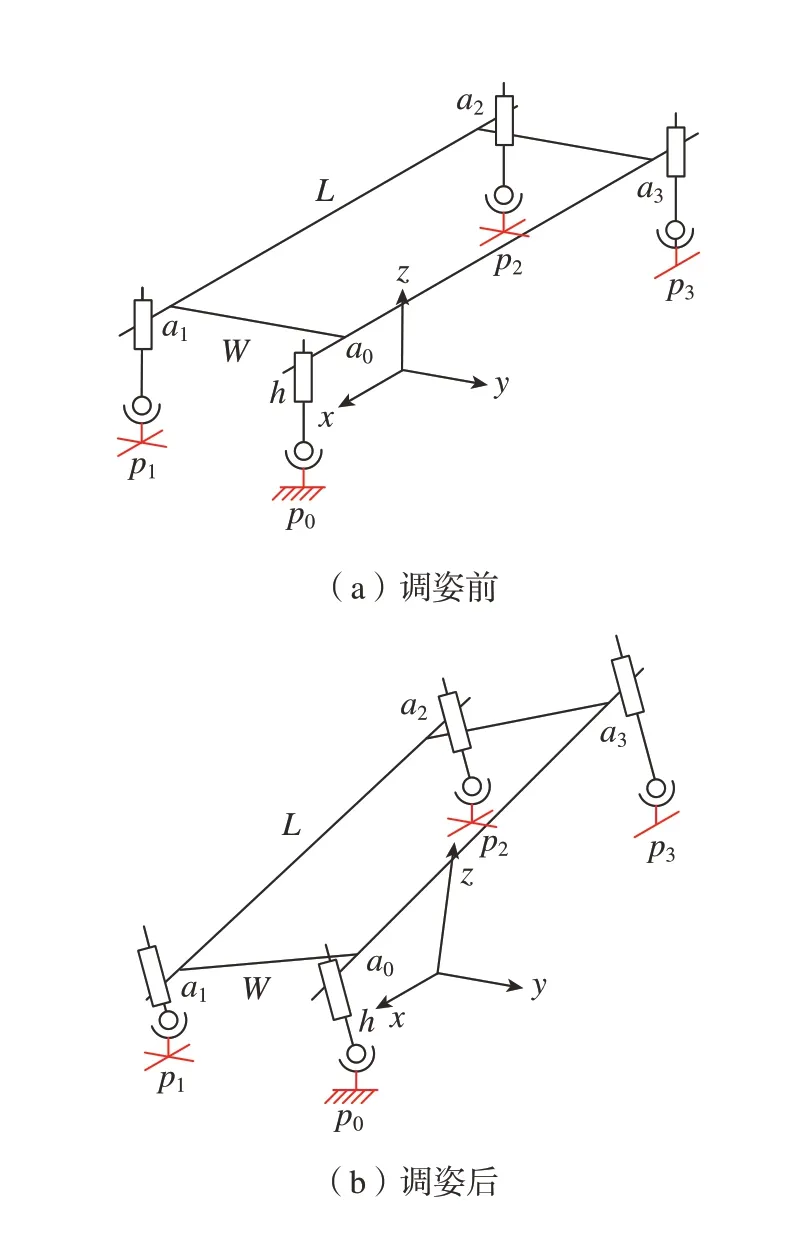
图4 旋量法调姿前后框架结构简图Fig.4 Sketch of the frame structure before and after posture adjustment using rotation method

分析为机器人先绕Y轴旋转后绕X轴旋转的旋转方式。由旋量法分析可得各个关节旋量为

式中，sij–yx为进行先Y后X调姿的第i个腿上第j个关节的旋量向量。其中，第0 个腿的第1 个关节为腿上球铰结构绕X轴的旋转关节，第0 个腿的第2 个关节为腿上球铰结构绕Y轴的旋转关节，第0 个腿的第3 个关节为腿上球铰结构绕Z轴的旋转关节；第1 个腿的第1 个关节为脚上沿X轴的平移关节，第1 个腿的第2 个关节为脚上沿Y轴的平移关节，第1 个腿的第3 个关节为腿上球铰结构绕X轴的旋转关节，第1 个腿的第4 个关节为腿上球铰结构绕Y轴的旋转关节，第1 个腿的第5 个关节为腿上球铰结构绕Z轴的旋转关节，第1 个腿的第6 个关节为腿上沿Z轴的平移关节；第2 个腿部关节与第1 个腿部关节相同；第3 个腿的第1 个关节为脚上沿X轴的平移关节，第3 个腿的第2 个关节为腿上球铰结构绕X轴的旋转关节，第3 个腿的第3 个关节为腿上球铰结构绕Y轴的旋转关节，第3 个腿的第4 个关节为腿上球铰结构绕Z轴的旋转关节，第3 个腿的第5 个关节为腿上沿Z轴的平移关节。进一步得到各个支链的初始矩阵为

式中，Miyx为进行先Y后X调姿的第i个腿的初始齐次变换矩阵，由此可得各个支链的旋量表达式为

式中，Tiyx为进行先Y后X调姿的第i个腿的齐次变换矩阵；θij为进行先Y后X调姿的第i个腿上第j个关节的运动量。其中，θ01、θ02、θ03、θ13、θ14、θ15、θ23、θ24、θ25、θ32、θ33、θ34为已知量，θ11、θ12、θ21、θ22、θ31、θ16、θ26、θ35为未知量。由此可构造方程组为

机器人4 条腿平行运动，且与机器人框架垂直，由此可以引入约束方程组

式中，t1为绕X轴旋转角度；t2为绕Y轴旋转角度；∆p1、∆p2、∆p3为调姿后腿部末端位置移动偏差。

式中，L1–yx、L2–yx、L3–yx为进行先X后Y调姿后各个腿长度。如此得到基准腿与其他3 条腿的长度表达式。

2.2 调姿正解计算

在已知基准腿和其余3 条腿的腿长后，也可以根据腿长反推框架绕X轴和Y轴的旋转角度。为了尽可能结合实际数据，使算法具有通用性，采用了拟合平面的方法。为计算简单，本次计算的坐标系将以机器人框架部位为基准，如图4 所示以a0为原点，向量为X轴正方向为Y轴正方向，计算拟合机器人脚部所在平面。根据上述的参数设置，并设4 条腿长分别为L1、L2、L3和L4。由此可得脚部的坐标为

可以得到3 个差值向量，用于计算工作平面的法向量，即

可以分别计算得到3 个法向量，即

由此可得到法向量的平均值为

归一化后可得

计算旋转矩阵的逆为

由旋转矩阵计算得到工作平面的法向量为

结合公式naver_norm的结果可得运动学正解为[2–3]

2.3 调姿分析

由于机器人调姿的旋转中心并不是身体中心，所以机器人的身体中心在调姿后将产生一定的位移，本节将对该位移大小进行定量的计算分析，阐述其对制造加工的影响。在运动前，框架中心的坐标为

在调姿后，框架中心的坐标为

由此可得，调姿过后，框架中心的位移为

其次，结合机器人的实际数据，设其实际的L=1100 mm，W= 900 mm，h= 100 mm，从当前x轴角度为1°，y轴角度为2°，分别调姿到5°和8°，将其代入式（13）进行计算，可以得到表1，对实际机器人的设计分析有一定的指导作用。

表1 调姿计算参数表Table 1 Pose adjustment calculation parameter table

在实际控制中，由姿态R1旋转到姿态R2，需要对旋转矩阵进行插值。传统的插值方法无法对旋转矩阵进行插值，同时为了保证运动流畅性，在此选择基于旋量的矩阵插值，计算公式为

通过设置α∈[0，1]，即可完成在两个矩阵之间进行插值，并可用于两个姿态下连续调姿的运动，对实际控制有一定指导意义。

3 纠偏运动计算分析

如图5（a）所示，在机器人运动过程中，由于摩擦、重力、内部作用力和振动等因素，机器人运动方向将不可避免地产生偏移，所以机器人需要纠偏的能力。在进行纠偏时，外框4 条腿都吸附在飞机蒙皮上，纠偏运动主要靠两侧外框的相对运动来实现。其中，红色部分表示该方向吸盘钳制器锁死，绿色代表该方向有自由度。当外框CD部分相对于内框有相对移动时，爬壁机器人本体方向会产生角度为θ的偏移，偏移后的位姿如图5（b）所示。

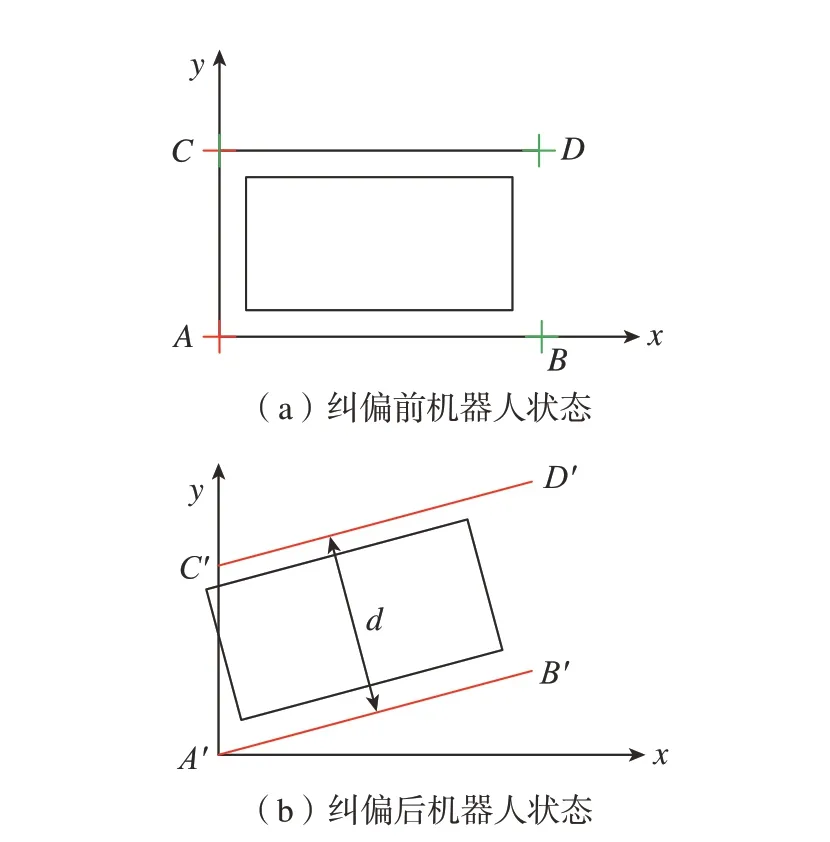
图5 纠偏过程机器人状态Fig.5 Robot status during deviation correction process

3.1 纠偏逆解计算

根据机器人配置将进行纠偏过程的逆解计算，设纠偏角度为θ，设直线A'B'的直线方程为

C'D'的直线方程为

则可以计算出两个外框之间的距离d为

从而计算得到b的值为

对于B、C、D点来说，其位移大小分别为

最后可以算得两个框架的相对位移为

由以上计算可以发现，通过使两个外框产生一个偏移量可以改变机器人整体的前进方向，从而完成纠偏工作。同时，如果锁住C点y方向钳制器可以防止在行进过程中整体结构绕Z轴旋转。由于纠偏的方向不固定，所以4 个吸盘都选择相同的结构（即两个方向都有自由度），方便在实际使用时进行控制。

3.2 纠偏偏解计算

由于纠偏过程的运动较为简单，其正解也容易求解。从式（31）可得运动学正解，即

3.3 纠偏分析

在调姿的运动过程中，机器人中心会产生偏移，而在纠偏的运动中，也有类似的现象。相对基准脚旋转后，会有机器人中心的偏置位移。本节将对该偏置位移进行定量分析。在纠偏前，框架中心的坐标为

在纠偏后，框架中心的坐标为

同时，与调姿过程一样，代入实际数据后可以计算纠偏角度与脚部位移的关系（表2），以此来指导机器人设计。

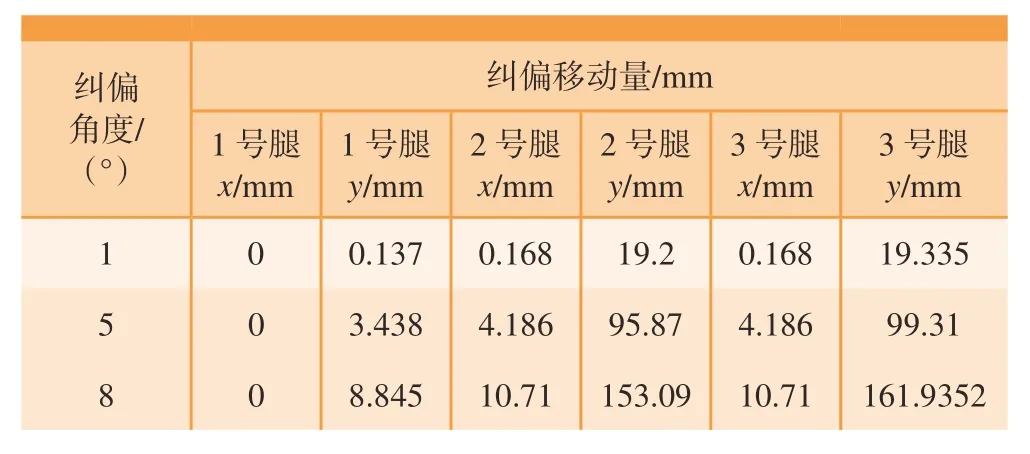
表2 纠偏计算参数表Table 2 Correction calculation parameter table

4 试验验证

本研究研制的爬壁制孔机器人样机主要用于验证机器人的行走与调姿的运动方案，所以取消了最后制孔末端的部件，如图6 所示，主要结构包括机器人的内外框架、腿部结构以及变自由度吸盘。安装惯性传感器检测试验结果，机器人具体参数如表3 所示。

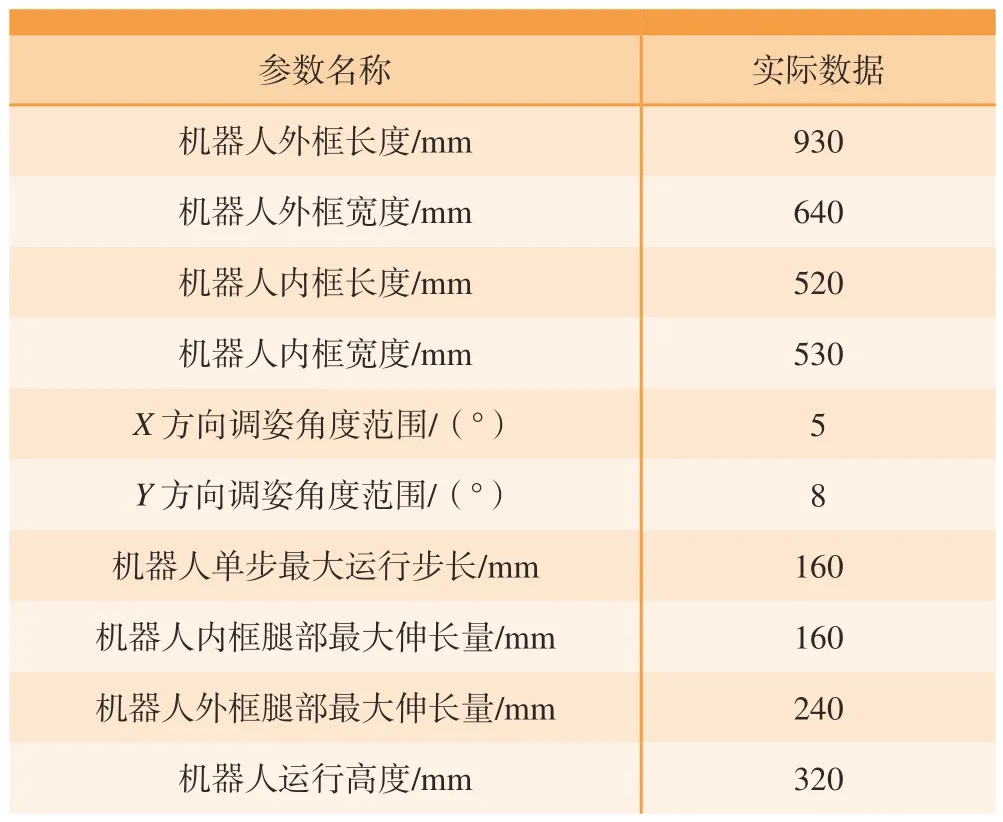
表3 机器人参数Table 3 Robot parameters

图6 爬壁机器人样机Fig.6 Wall-climbing robot prototype

在试验中，机器人的电机编号如图7 所示，一共有10 个电机，1 号、4 号、5 号、8 号4 个电机属于外框腿部运动，2 号、3 号、6 号、7 号4 个电机属于内框腿部运动，9 号和10 号两个电机属于内外框相对运动。惯性传感器的row、pitch、yaw 角分别对应机器人绕Y轴、X轴和Z轴的旋转，在试验中仅用到row 角和pitch 角，yaw 角与试验无关，后续不会出现在数据中。

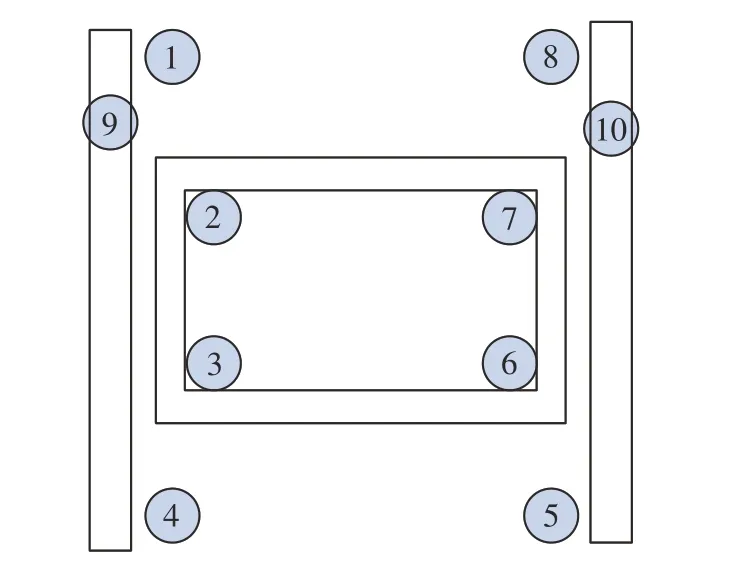
图7 电机编号图Fig.7 Motor numbering diagram

试验主要用于验证机器人XY轴联合调姿的能力，验证运动学分析中XY轴调姿运动相互独立的推论。设计试验中XY轴分别进行3°的调姿运动，运动后再复位，试验数据如表4、图8和9所示，由惯性传感器数据可得，XY两轴的角度变化是独立进行的，互不干扰，与试验预期相符，验证了运动学理论分析的正确性与机器人控制的可行性。

表4 XY 轴调姿与复位惯性传感器数据Table 4 XY axis attitude adjustment and reset inertial sensor data

5 结论

（1）对机器人的调姿以及纠偏运动进行自由度分析，并给出了每个足部相应的XY方向的锁死放开方案，使得机器人自由度变为1，进而使得机器人在运动调姿过程中运动可控。

（2）研究了机器人调姿以及纠偏的运动学，并根据旋量法利用不同腿部作为不同支链，构造从坐标系原点到机器人框架末端的旋量方程，利用不同支链下末端的最终位置相同这一特点，结合机器人的结构特性进行约束，构造方程组，进行未知变量的求解，得到腿长和脚部位移等的实际解。并制作出样机进行实际解试验，验证了试验结果的正确性。

以上结论可以用于指导机器人设计及控制，具有一定的实际意义。