打印方向对SLM 增材制造点阵结构力学性能的影响分析

王晓阳，孙 辽，胡全栋，韩永志，朱小军

（1. 航空工业第一飞机设计研究院，西安 710089；2. 中国航空制造技术研究院，北京 100024）

自然界中的轻质结构 （如植物根茎、鸟骨、竹子等）在细观层面上均展现出“疏松多孔”的特性，这种多孔结构赋予了结构轻质及多功能的特性[1]。受此启发，周期性桁架状的点阵结构越来越被航空航天、汽车制造及医疗行业关注。这类结构拥有良好的可设计性及物理、力学性能，例如较高的比强度、比刚度，以及隔热和降噪功能等。近些年增材制造技术的高速发展，尤其是选区激光熔化 （Selective laser melting，SLM）技术的不断成熟，为高性能金属点阵结构的制造和应用提供了极大的便利，提高了设计自由度[2]。

点阵结构力学性能分析方法包括解析法、数值仿真法和试验法[3]。在点阵结构打印过程中不可避免地出现各种缺陷，包括支杆弯曲、直径分布不均及支杆空心等，这些缺陷导致点阵结构力学性能理论值与试验值存在较大误差[4]。朱健峰等[5]针对4 种不同构型点阵单胞的力学性能进行了理论、试验及有限元分析，结果表明，仿真结果与试验的误差接近30%。通过CT 扫描，重构点阵结构实际模型并对含缺陷的有限元模型进行分析，可得到更加接近试验结果的仿真解[6]。增材制造的质量与打印过程中零件的悬垂角密切相关，由于点阵结构中各支杆的空间角度呈周期性分布，不同角度支杆的缺陷呈现出不同特征，从而影响最终的点阵结构力学性能[7–8]。本文以面心立方 （PC）点阵结构为研究对象，研究打印方向对该类结构力学性能的影响。主要研究分为两步： （1）基于均匀化方法得到点阵单胞理论的等效力学性能； （2）针对不同打印方向制造的点阵结构进行单轴正压试验，通过对不同打印方向试样的试验结果对比，得到增材制造打印方向对点阵结构力学性能的影响。

1 点阵结构等效力学性能计算

基于均匀化方法，对点阵结构代表体元 （RVE）进行分析，通过对RVE 施加周期性边界条件，采用应变能等效的原则即可求解点阵结构等效性能[9]。图1 展示了尺寸为L0的立方体RVE 在受到1 方向单轴拉伸及1– 2 平面内纯剪切应变尺寸变化图 （L1、L2和L3分别为RVE 在单轴拉伸应变作用下单元尺寸变化；h为单元受到纯剪切应变时2 方向最大位移）。在点阵单胞线弹性小变形的假设下，其1 方向等效杨氏模量由式（1）计算，其中为施加在RVE 上1 方向的单位应变；为单元1 方向的等效平均应力，该应力可通过有限元中提取参考节点1 方向的支反力F1计算。等效泊松比和由式（2）和（3）得到。与求解等效杨氏模量方法类似，通过提取RVE1–2 平面内纯剪切应变时的支反力F12，由式（4）可计算出点阵结构的剪切模量。

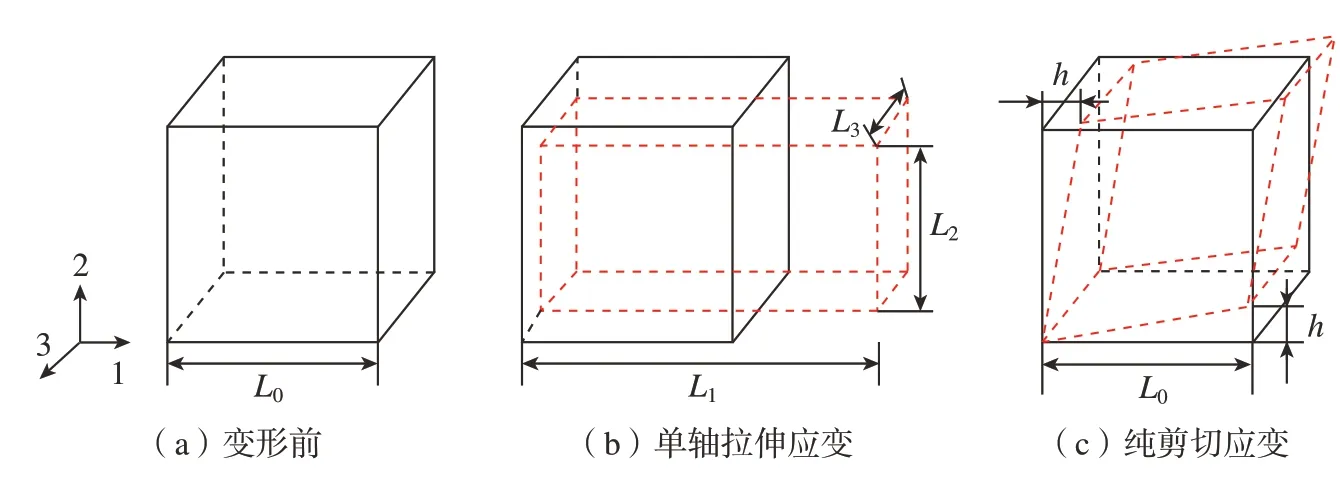
图1 周期性RVE 均匀化方法边界条件示意图Fig.1 Schematic diagram of boundary conditions for the periodic RVE homogenization method

PC 点阵RVE 元均具有3 个正交的对称平面，并考虑到同一个点阵单胞内支杆半径均相同，这种点阵结构可等效为准各向同性的点阵结构，因此其杨氏模量、剪切模量及泊松比满足式 （5）～（7）。

基于均匀化理论，利用文献[9]中的方法对Abaqus 进行二次开发，可实现对点阵RVE 快速施加周期性边界条件。通过对单胞进行单轴拉伸、纯剪切数值仿真试验，利用式（1）～（4）求解出点阵结构等效杨氏模量、等效剪切模量及泊松比。点阵结构母材Ti–6Al–4V 杨氏模量E0=110 MPa，泊松比μ0=0.34，最终得到PC 点阵结构相对等效模量及泊松比，如图2 所示。

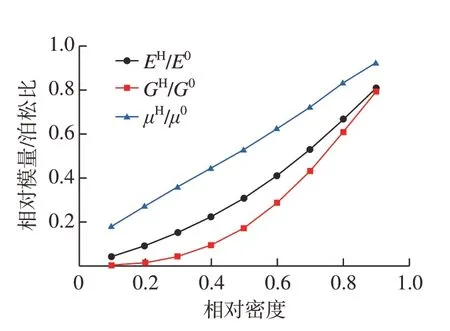
图2 PC 点阵结构等效模量/泊松比曲线Fig.2 Effective modulus and Poisson’s ratio curves of PC lattice

2 PC 点阵准静态压缩试验

2.1 样件制备

点阵试样采用Gd5 等级的Ti–6Al–4V 粉末制造，粉末粒径15～53 μm、层厚0.04 mm。激光功率320 W、光斑直径100 μm、扫描间距0.14 mm、扫描速度1200 mm/s。采用电火花线切割工艺将试样从打印平台取下，并在800 ℃下保温4 h 进行热处理。图3（a）为点阵试样示意图，试样为30 mm×30 mm×30 mm 的立方体结构，由10 层10×10 的PC 点阵单胞组成。点阵单胞如图3（b）所示,单胞尺寸L0为3 mm。点阵单胞的相对密度由式 （8）确定。

图3 PC 点阵试样SLM 制备示意图Fig.3 Schematic diagram of the SLM fabricated PC lattice specimens

式中，ρH及ρs分别为点阵单胞及母材密度。

点阵试样按0.1、0.3、0.5、0.7 4类不同的相对密度设计。图3（c）为试样在制造中采取不同的打印悬垂角β示意图，底面A为试样最终放置在试验机平台上的平面，β为试样承载支杆（在单轴压缩试验中平行于加载方向的支杆）与打印平台的夹角，β取0°、30°、45°、60° 4 组值用于表征不同的打印方向，每组3件。点阵试样制造过程如图3（d）所示，最终试样实物及编号如图3（e）所示。点阵试样实际相对密度按式（9）计算。

式中，m*和L分别为点阵试样实测质量及立方体点阵尺寸。

点阵试样相对密度设计值与实测值见表1。由于在激光选区熔化成形过程中，金属点阵结构表面粘有部分未熔化的合金粉末，导致实测值相对密度相较设计值偏大。

表1 点阵试样相对密度设计值与实测相对密度平均值对比Table 1 Designed values of relative density and the averaged values of the measured relative density of the PC lattice specimens

2.2 形貌分析

采用光学显微镜对上述PC 点阵试样的微观形貌进行观察。图4展示了各组PC 点阵试样在不同打印方向下支杆的典型微观形貌图，4组试样均未出现明显的支杆弯曲，可忽略增材制造产生的支杆弯曲对后续正压试验的影响。其中红色箭头为打印方向，承载支杆竖直放置，承载支杆上标记的短红线表示材料层的堆叠，每个显微照片中央标记的角度表示承载支杆的悬垂角β。

图4 点阵试样支杆微观形貌Fig.4 Optical micrographic demonstration of the details of the PC lattice specimens

从图4（a）可以看出，在相对密度ρ-*= 0.1138、β=0 时承载支杆表现出较严重的制造缺陷，如黄色椭圆区域中的球状物黏附，以及黄色梯形区域内的支杆几何不规则性。随着β的增大，上述制造缺陷减少，当β=90°时，承载支杆达到了最佳的几何精度。这种球状挂渣及几何不规则的形成原因为：当β=0 时，承载支杆的悬垂角过小，在打印过程中会出现由于粉末融化凝固造成下陷，或由于激光束功率偏高、成形速率过快，合金粉末颗粒度较细导致局部过热引起的粘粉或存在未熔融颗粒[10]。随着点阵结构相对密度的增加，不同β角的承载支杆的制造缺陷差异减小。当相对密度增加到ρ-*= 0.5168时，承载支杆的颗粒黏附效应和几何不规则性明显降低。这是由于随着支柱直径的增加，两个支杆节点之间的支柱悬垂部分的长度减小，较短的悬垂支柱有助于减少上述几何制造缺陷出现。

2.3 试验过程

采用MTS E64 电子万能试验机进行点阵结构单轴压缩试验，试验在室温下进行，位移加载速度为1.5 mm/min。压缩试验按照ISO 13314：2011 标准执行，试验如图5 所示。试验中，确保承载支柱沿加载方向，将PC 晶格试样放置在上、下压台之间，压台与试样之间的接触面使用二硫化钼润滑剂润滑，以减少压缩过程中试样垂直于加载方向膨胀时接触界面之间的摩擦力。试验中采用固定在两个压板上的位移引伸计测量试样沿加载方向的位移。分别选用50 t级及150 t 级的试验机对相对密度0.1、0.3 和0.5、0.7 的点阵试样进行加载，以保证测量精度；同时对与压板接触的试样表面进行线切割精加工，保证两个接触面的平面度及平行度不大于0.3。

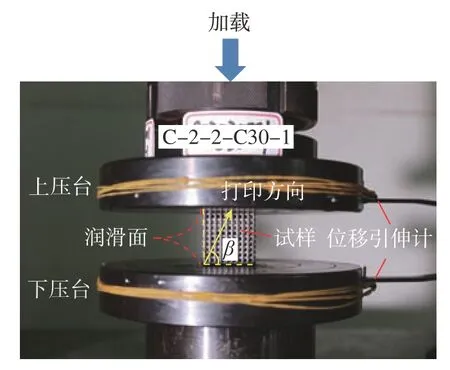
图5 试验示意图Fig.5 Schematic diagram of the test

2.4 试验结果

点阵试样的等效应力及等效应变按式（10）和（11）计算。

式中，F为加载载荷；∆L为试样的压缩量。

最终得到图6 所示的不同打印方向下试样的等效应力–应变曲线，可以看出所有试样在等轴压缩的初始阶段等效应力–应变均呈线性关系，直至发生屈服。对于较低相对密度的点阵结构 （= 0.1138 及= 0.3177），在压缩破坏过程中呈现“多波峰”现象，即等效应力超过第1个波峰发生破坏后，可继续承载，后相继出现多个应力峰值，但等效应力峰值随应变的增加而减小。这种“多波峰”的破坏现象是由于较低相对密度点阵结构逐层坍塌破坏引起的，如图7 所示。在试验中这种逐层坍塌无特定规律，主要原因是低密度点阵结构的制造缺陷相对较多，且对打印方向比较敏感，在制造过程中，这些缺陷随机分布，造成局部“薄弱层”。在压缩过程中，薄弱层过早破坏，其他层未完全破坏，还具有承载能力，所以这类相对密度较低的点阵结构呈现出“多波峰”破坏模式。相对密度较大的点阵结构 （= 0.5168及= 0.7076），呈现出较为相似的破坏模式，如图7 所示，均为沿对角剪切的一次性破坏，类似于实心块等轴压缩试验。这是由于随着相对密度的增大，点阵结构的缺陷减少并对打印方向不敏感，从而造成相同破坏模式。可以看出，随着相对密度的增加，点阵试样的变形行为呈现出向实心块状试件发展的趋势，其他相关文献研究中亦可以找到类似的破坏模式[11]。

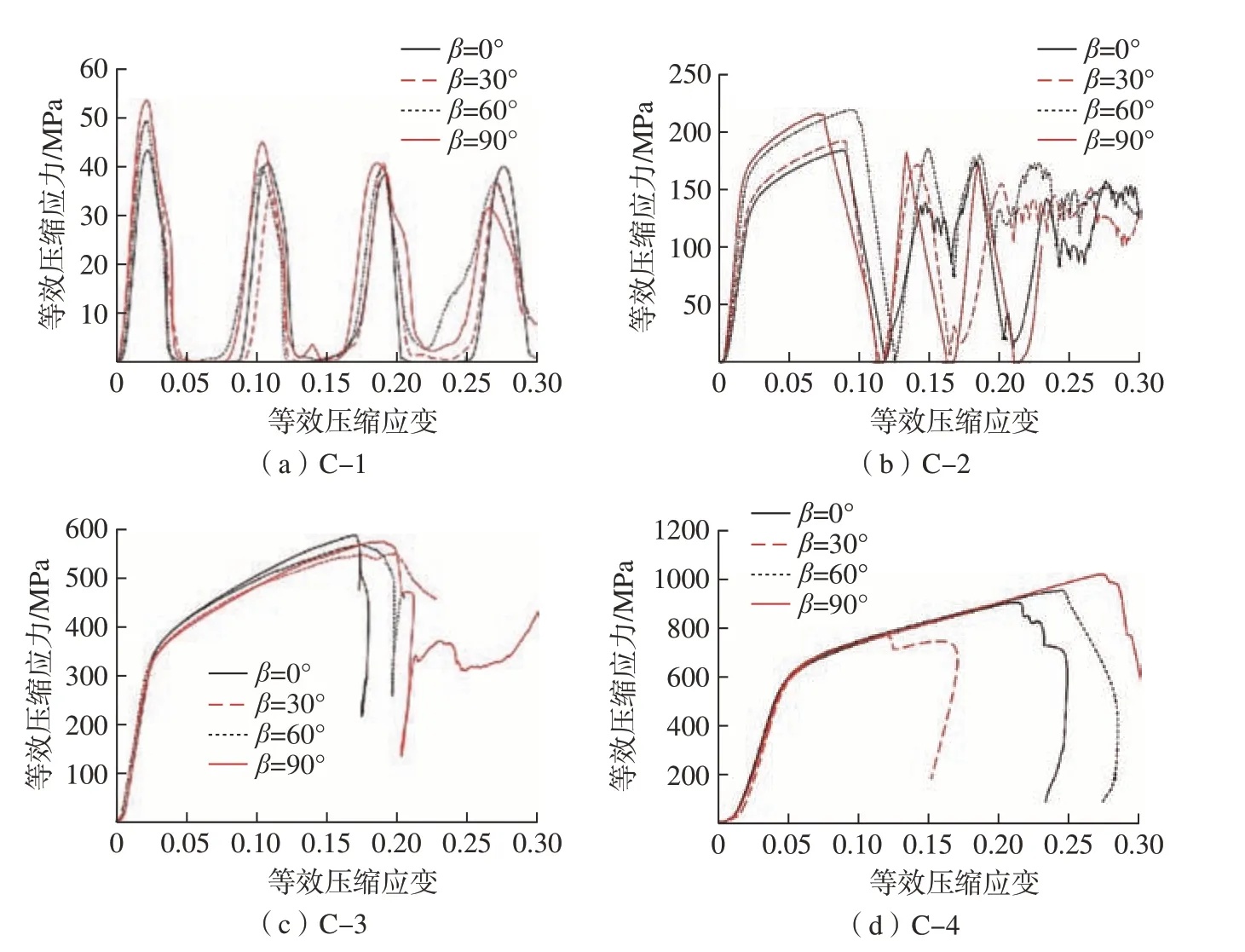
图6 点阵试样等效应力–应变曲线Fig.6 Stress – strain curves of the PC lattice specimens

图7 PC 点阵试样破坏模式示意图Fig.7 Schematic diagram of the failure modes of the PC lattice specimens

为直观揭示各组试验结果及仿真结果的差异，将同一相对密度下点阵结构的等效杨氏模量进行归一化处理，图8 列出了各组试样归一化等效杨氏模量的仿真结果及试验值。由于忽略了增材制造缺陷，基于均匀化方法的有限元仿真结果相较试验结果偏高，同时随着点阵结构相对密___度增大，在SLM 成形过程中，致密的点阵结构造成过高的温度梯度，制件内部存在较高的残余应力，影响试件最终承载能力，导致随着相对密度的增加，仿真结果的精度下降[12]。

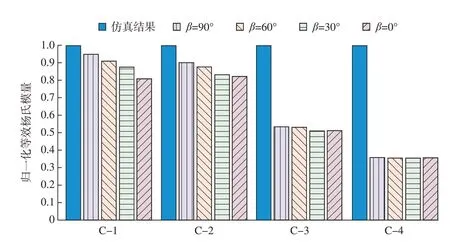
图8 打印方向对PC 点阵试样等效杨氏模量的影响Fig.8 Effects of building direction on the equivalent Young’s modulus of the PC lattice specimens

在同一相对密度下，打印悬垂角β增加使试样等效杨氏模量增加，在β=0°时等效杨氏模量最低。相对密度为0.1138 时，β=0°比β=90°的试样等效杨氏模量降低14.6%，此结果符合图4 中微观形貌结果，随着β角的增大，试样的缺陷不断减小，从而等效杨氏模量不断提高。此外，图8 还表明，随着相对密度增大，打印方向对等效杨氏模量的影响不断降低，当相对密度增加到0.7076 时，不同打印方向试件的等效杨氏模量十分接近。

3 结论

（1）试样微观形貌结果表明，点阵单胞支杆增材制造缺陷随支杆悬垂角增加而减小，同时低密度点阵结构支杆缺陷对打印方向更加敏感。

（2）准静态轴压测试结果表明，试样的等效杨氏模量在不同悬垂方向上存在一定的各向异性，数值随着支杆悬垂角度差异的增加而变大，随着点阵单胞相对密度的增加而减小。在相对密度为0.1138 时，最大差异达14.6%。

（3）由于基于均匀化方法数值仿真计算忽略了增材制造引起的缺陷，导致点阵结构力学性能仿真结果相较试验测试偏高，且随着点阵结构相对密度的增大，仿真结果精度下降，在相对密度为0.1138 时，仿真结果与试样平均值差异为11.3%，在相对密度为0.7076 时，差异达到65%。