弹道双区截装置弹丸瞬时速度测试方法研究

李 海，郑晨皓，赵平伟，倪晋平，武志超

（1.西安工业大学 光电工程学院，陕西 西安 710021；2.西安机电信息技术研究所，陕西 西安 710065）

引言

现代兵器在枪、炮、弹、药的研制和生产中，测量的主要参数包括弹丸飞行速度、飞行姿态、射击密集度、飞行时间等，其中弹丸飞行速度是评价装备性能的关键参数。在采用光幕阵列测量射击密集度[1-3]和炸点位置时，速度测量精度还影响测量参数的测量精度。目前兵器试验场应用较多的非接触式区截测速装置有线圈靶、光幕靶、天幕靶等，上述装置测试原理简单，可靠性高。采用上述装置构建的区截测速系统中，测量结果是弹道上两个区截装置间的弹丸飞行平均速度，亦为两个装置中点处的瞬时速度。但如果以该速度为基准推算测量区域附近任意位置的瞬时速度，会造成较大的测量误差[4-6]。例如，在近炸引信的研制试验和生产校验任务中，检验引信合格与否的一个重要标准是测量装有该引信的脱靶量。使用六光幕阵列天幕立靶进行弹丸空间炸点脱靶量参数测试，首先通过六光幕阵列测得空间弹道和弹丸速度，再利用炸点火焰探测器获得炸点爆炸时间，即可得到炸点在空间的三维坐标。该方法假设弹道为匀速直线，并未考虑弹丸在飞行过程中空气阻力对速度造成的影响。天幕立靶测得的速度值近似等效为两靶布放位置连线中心的瞬时速度，该中心点为天幕立靶测速点。实际测试中测速点和炸点通常相距较远，约20 m 左右，使用天幕立靶测速点的瞬时速度等效炸点位置处的瞬时速度，将引起较大的脱靶量测试误差[7-9]。同样，弹丸出炮口初速度通常使用天幕靶等区截测速装置测量，将测量结果修正后得到。沿弹道方向依次布设两台测速天幕靶，通过精确测量弹丸穿过天幕靶光幕的时间，再测量两靶间距后，计算得到两靶布放位置连线中心的弹丸瞬时速度，该中心点即为天幕靶测速点。然后再测量测速点到炮口的距离，通过对应的弹形系数、温湿度、西亚切常量、弹丸质量等多种参数计算弹丸的炮口初速度[10-13]。修正算法中存在大量需要人工测量、查表近似的参数，不仅操作繁琐，而且会引入一定的误差[14-16]。

本文考虑弹丸非匀速运动下，由于空气阻力造成弹丸速度衰减，于是提出采用两套区截测速装置精确测量一段弹道任意位置处的瞬时速度，期望达到减小瞬时速度测量误差的目的。

1 基于区截测速的弹丸瞬时速度测试原理

为了简化，限定弹丸形状为球形或者是旋转对称体，不涉及带尾翼的弹丸，或飞行过程中有脱离破片及形状为非对称的其他弹丸。弹丸在飞行过程中受空气阻力、重力等各种因素的影响，当弹道近似水平，俯仰角在正负5°以内时，可以忽略重力对弹丸速度的影响。当弹丸为标准球体或其迎风角度近似为零度时，仅存在空气阻力对弹丸速度的影响。此时由于目标的对称关系，法向力、俯仰力矩均为零，只有轴向力作用于弹体，则弹丸受到的空气阻力和瞬时速度的关系可表示为

式中：F为弹丸受到的空气阻力；m为弹丸质量；a为加速度；ρ为空气密度；S为弹丸圆柱部分最大横截面积；Cx为迎风角度为零时的弹丸阻力系数；Ma为马赫数，表示速度和音速的比值；v为弹丸速度。某型标准弹丸阻力系数和马赫数的函数关系如图1 所示，该曲线数据通常通过风洞实验获得。

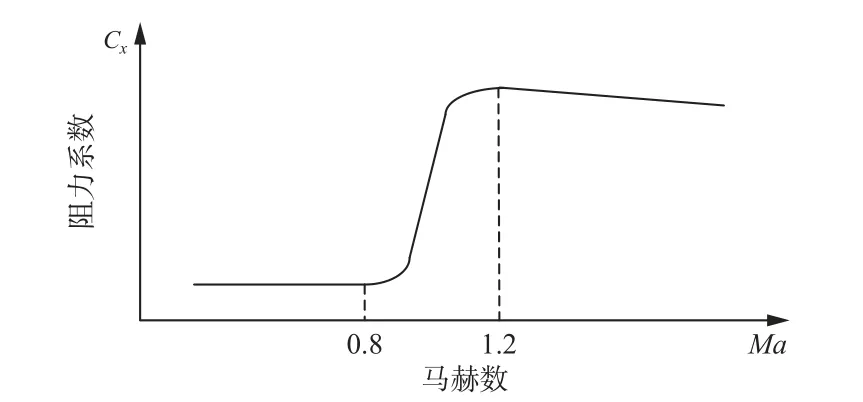
图1 阻力系数与马赫数的关系Fig.1 Relationship between resistance coefficient and mach number

由图1 可知，当速度小于0.8 倍音速时，阻力系数曲线为水平直线段，阻力系数近似于常数；而当速度大于0.8 倍音速时，阻力系数可以表示为分段比例函数。本文首先研究速度小于0.8 倍音速时的速度变化规律，此时弹丸在空气中飞行时受到的阻力即弹丸飞行的加速度和弹丸速度的平方成正比。而当弹丸速度高于1.2 倍音速时，阻力系数曲线可以近似为斜率较小的直线。当测试区域不大时，弹丸速度变化较小，造成的阻力系数变化也很小，可以等效为常数。因此，本文研究的算法在弹丸速度高于1.2 倍音速时依然适用，实验通过步枪弹的数据也验证了这一点。

因为在每次射击实验中，弹丸飞越测试区域的时间通常为几个到几十个微秒，在这段时间内空气密度、弹丸圆柱部分最大横截面积、弹丸质量、弹丸阻力系数等参数几乎不变，可以等效为常数B，即，代入式（1）得，通过解方程可得：

通过式（2）～式（6），就可以完成弹道某点瞬时速度测量，该测速点称为解算测速点。如图2 所示，采用两套区截测速装置，依次沿弹道线布放，两套区截测速装置的测速点相距为s0。第一套测量速度为v0，近似为测速点处的瞬时速度，称该测速点为第一测速点；第二套测量速度为v1，称其为第二测速点处的瞬时速度。t为弹丸从第一测速点飞行到解算测速点的时间，S为第一测速点与解算测速点的间距，v为弹丸飞越解算测速点时的瞬时速度。

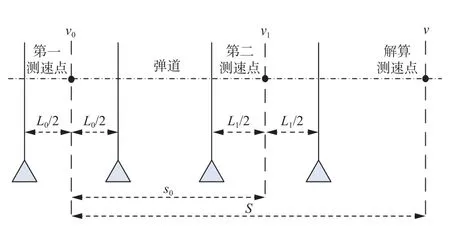
图2 双区截测速示意图Fig.2 Schematic diagram of double zone-block velocity measurement

首先，通过式（2）计算出参数B，B包含了阻力系数、空气密度、弹丸圆柱部分最大横截面积、弹丸质量等信息；然后，通过式（3），在确定参数B并已知第一测速点速度v0的条件下，可以计算弹丸通过第一测速点t时间后的瞬时速度v；通过式（4），在确定参数B并已知第一测速点速度v0的条件下，可以计算第一测速点与解算测速点间的距离S，即弹丸通过第一测速点后t时间的实时位置，该公式可以用于精确测量空间炸点脱靶量参数；通过式（5），在确定参数B并已知第一测速点速度v0的条件下，可以计算弹丸通过第一测速点后沿弹道线方向的距离S处弹丸的瞬时速度v，该公式可以测量弹丸的炮口初速度，和现有方法进行比较，不需查表确认参数，简化了测量过程，并且提高了测量速度和精度；最后通过式（6），在确定参数B并已知第一测速点速度v0的条件下，可以计算弹丸从第一测速点开始沿弹道方向到距离S处的时间t。

2 单套区截装置测量瞬时速度误差分析

对速度衰减公式在区截测速原理中的应用进行误差分析。

1）预设弹道垂直入射，第一个区截幕面位置固定，第二个区截幕面位置连续变化，测速点位置在第一和第二区截幕面之间连续变化，验证区截测速点的瞬时速度和平均速度的误差变化规律。

设弹道某一点为第一测速点，该位置的弹丸瞬时速度为v0，沿弹道方向距离第一测速点2 m 处为区截第一幕面位置，区截第二幕面和第一测速点的距离变化区间为2 m～20 m。解算测速点和第一测速点的距离变化区间为2 m～10 m，设弹丸速度衰减系数B为0.001，v0为100 m/s。应用式（6）分别计算弹丸通过区截第一、二幕面的时间，通过过幕时间和两个幕面的距离可以计算两个幕面间的平均速度，又通过式（5）可以计算测速点处的瞬时速度。仿真结果如图3 所示，速度误差为平均速度和瞬时速度之差的绝对值。

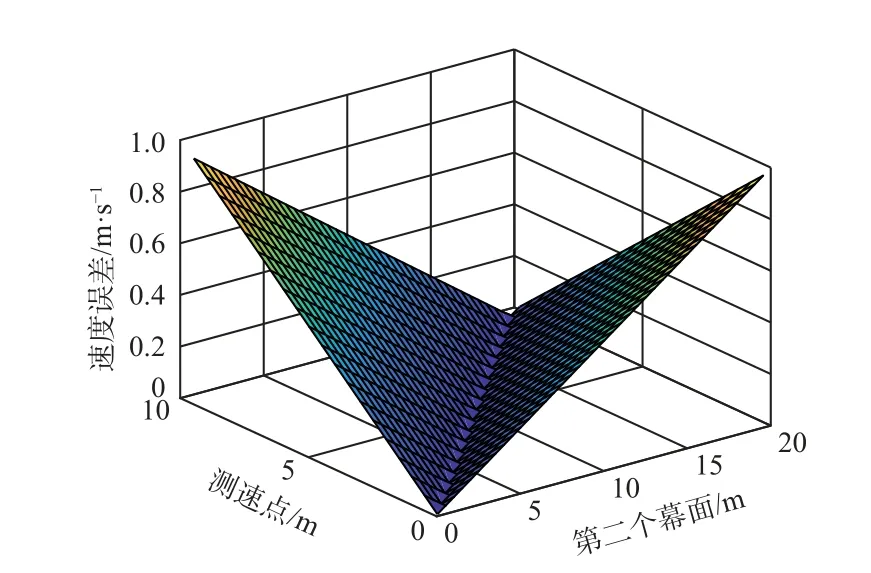
图3 测速点位置对误差的影响Fig.3 Influence of velocity measuring point position on errors

表1 为图3 中的误差数据列表，第二幕面位置变化的步进值为0.2 m，测速点位置变化的步进值为0.1 m。可以看出误差随距离为线性变化，并且在区截中心时出现最小值，该最小误差会随着区截间距增加而变大，当间距为4 m 时误差为0.03×10-4m/s，当间距为8 m 时误差为0.01×10-3m/s。

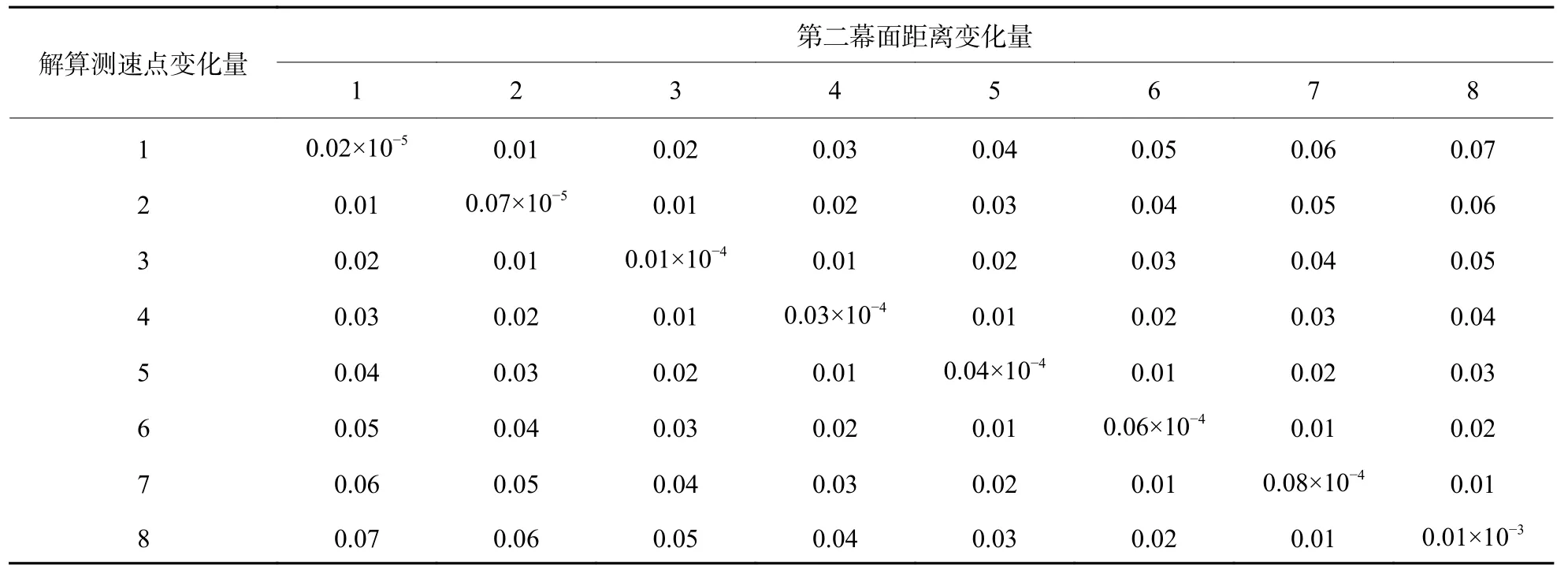
表1 测速点误差数据Table 1 Error data of velocity measuring points m/s

2）设区截测速幕面间距发生变化，解算测速点位置在第一和第二区截幕面的中心位置处，验证区截幕面间的平均速度和中心位置瞬时速度的误差随区截幕面间距变化的规律。

图4 是区截幕面间距变化时速度误差的变化，表明区截幕面间的平均速度和中心位置瞬时速度的误差随区截距离的减小而减小。

图4 区截幕面间距对误差的影响Fig.4 Influence of interception plane spacing on errors

3）设第一个区截幕面位置和第二个区截幕面位置均固定，测速点位置在第一和第二区截幕面的中心位置处，验证区截幕面间的平均速度和中心位置瞬时速度的误差随速度衰减系数B和第一测速点速度v0变化的规律。

图5 为当衰减系数B在0.001～0.02 区间变化且v0在50～200 m/s 区间变化时产生的测量误差，误差值随B的增大或v0的增大而增大。图6 为该过程的相对误差，该误差仅随B的增大而增大。表明区截幕面间的平均速度和中心位置瞬时速度的相对误差与弹丸速度大小无关，但B值越小该误差越小，表明B值不仅和速度衰减速度有关，而且和速度衰减后产生的误差有关。

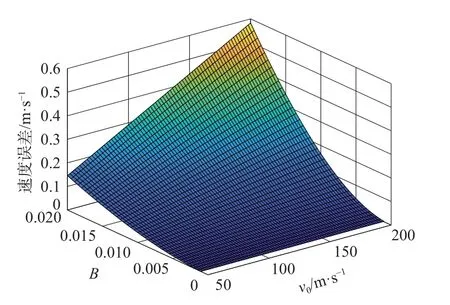
图5 衰减系数B 的误差Fig.5 Error of attenuation coefficient B

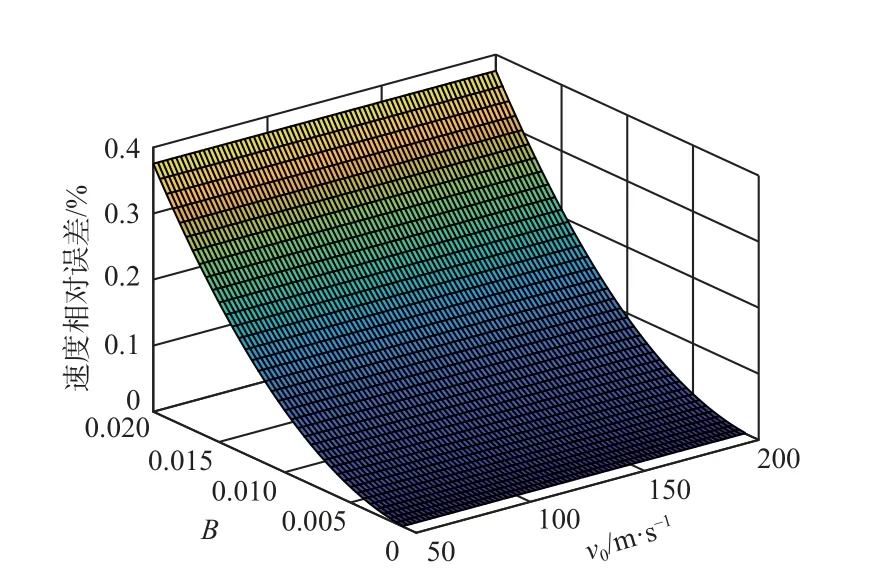
图6 衰减系数B 的相对误差Fig.6 Relative error of attenuation coefficient B

仿真结果表明，在B值不大、区截间距也不大的情况下，采用区截装置和本文建立的测试模型对测试区域某位置的瞬时速度进行测量是可行的，其精度可以接受。

3 双套区截装置测量瞬时速度误差分析

本节主要研究本文提出的双区截测试瞬时速度方法的测量误差。

1）通过v0和B的变化观察误差的变化规律。仿真条件：s0=3.0 m，S=4.0 m，v0变化区间50 m/s～200 m/s，v0最大误差0.001 m/s，距离测量最大误差0.001 m，B变化区间0.001～0.02。

图7、图8 分别是v0和B变化时的速度误差和速度相对误差。图7 表明误差随B和v0的增大而增大，图8 表明相对误差随B的增大而增大，随v0的增大而减小。相对误差和B的变化规律近似线性，v0在0～100 m/s 间相对误差变化较大，在100 m/s～200 m/s间的变化较小且近似线性，最大相对误差小于0.004 5%。

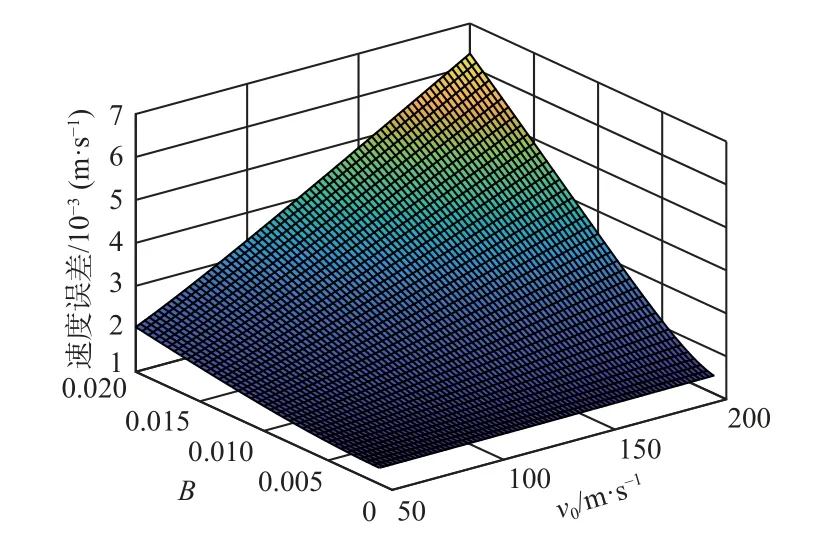
图7 速度误差Fig.7 Velocity error

图8 速度相对误差Fig.8 Velocity relative error

2）通过v0和S的变化观察误差的变化规律。仿真条件：s0=3.0 m，B=0.01，v0变化区间50 m/s～200 m/s，S变化区间-2 m～10 m。

图9、图10 分别是v0和S变化时的速度误差和速度相对误差。图9 表明，速度的误差随着S和v0的增大而增大；图10 表明，速度的相对误差随着S的增大、v0的减小而增大。误差在1 m 附近存在最小值，最大相对误差不超过0.01%。

图9 速度误差Fig.9 Velocity error

图10 速度相对误差Fig.10 Velocity relative error

上述误差仿真表明，在速度小于0.8 倍音速时，最大相对误差小于0.01%，满足测试精度要求，并说明了影响误差的各个因素及其方式和规律。

4 实弹试验验证

采用弹弓、气枪、步枪分组进行实弹射击实验。实验采用原像反射式激光光幕靶，形成区截光幕速度测试装置，使用专用数据采集设备进行信号采集和分析处理，得到弹丸过幕的精确时间。弹弓和气枪实验使用4 个光幕，任意2 个光幕均可构成一套区截测速装置。本实验采用光幕1、2 形成第一套区截装置，光幕1、3 形成第二套区截装置，第一测速点到第二测速点间距s0为375 mm，解算测速点设置为2、3 光幕的中心位置，到第一测速点距离S为750 mm，光幕布放如图11 所示。

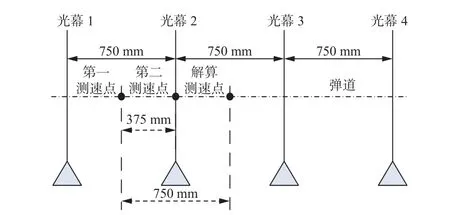
图11 光幕布放示意图Fig.11 Schematic diagram of light curtain arrangement

图12 为实验现场照片，图13 为弹丸过幕时间采集软件界面。通过弹丸过幕时间采集软件，能采集有效弹丸信号，从而获得过幕时间。

图12 实验现场图Fig.12 Experimental site

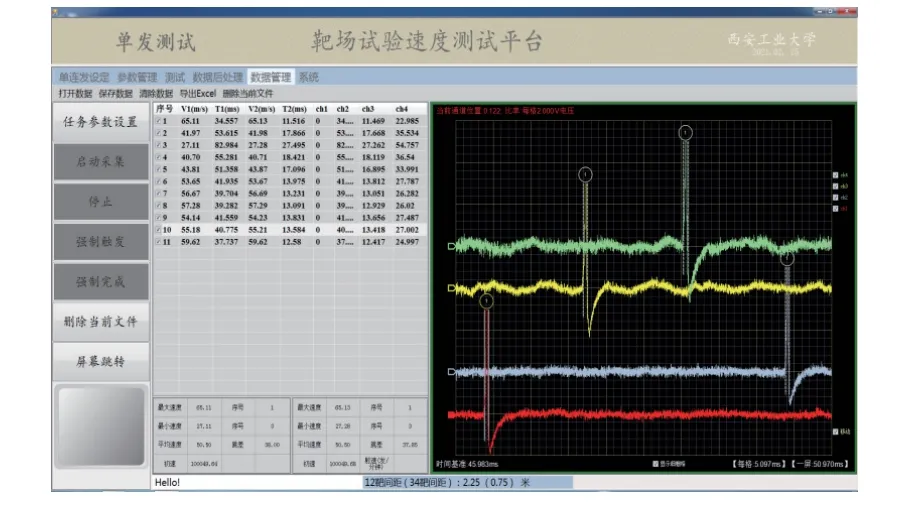
图13 弹丸过幕时间采集软件界面Fig.13 Acquisition software interface of projectile passing time

应用式（2）和式（5），分别计算衰减系数B和弹丸速度v，软件界面如图14 所示。

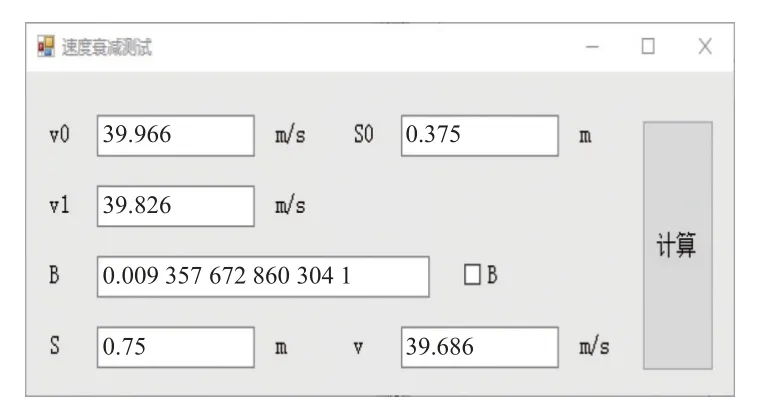
图14 计算衰减系数和弹丸速度的软件界面Fig.14 Software interface for calculating attenuation coefficient and projectile velocity

填入v0、v1和S0计算可得B值，再填入S计算得到v。将v和同一测试点处单套区截装置测试得到的v进行比较，得到测试误差数据如表2～表5所示。表2～表5 分别给出了弹弓发射6 mm 钢珠、弹弓发射10 mm 泥丸、气枪发射6 mm 钢珠、弹道枪发射7.62 mm 弹丸四种试验条件下所得测试数据。

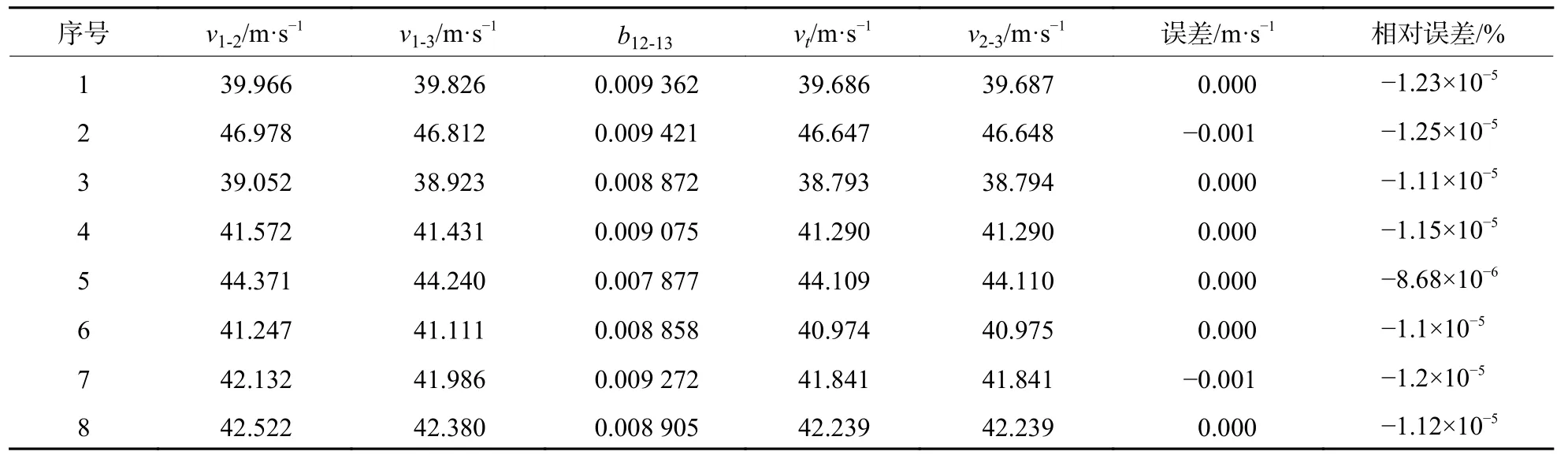
表2 弹弓发射6 mm 钢珠测试数据Table 2 Test data of slingshot shooting 6 mm steel ball

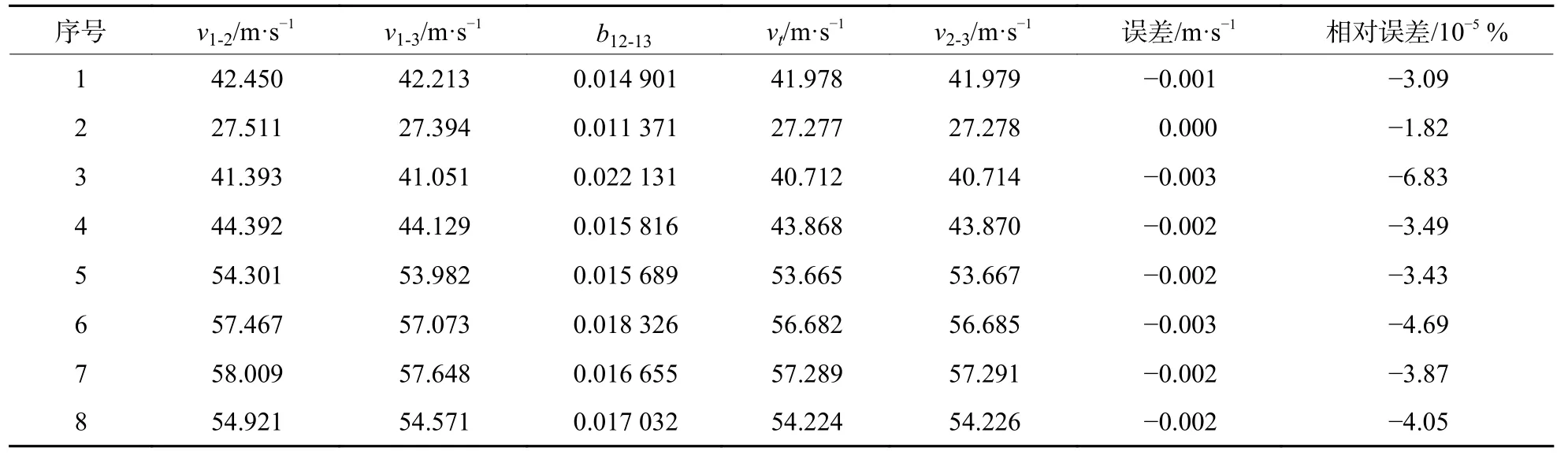
表3 弹弓发射10 mm 泥丸测试数据Table 3 Test data of slingshot shooting 10 mm mud pellet

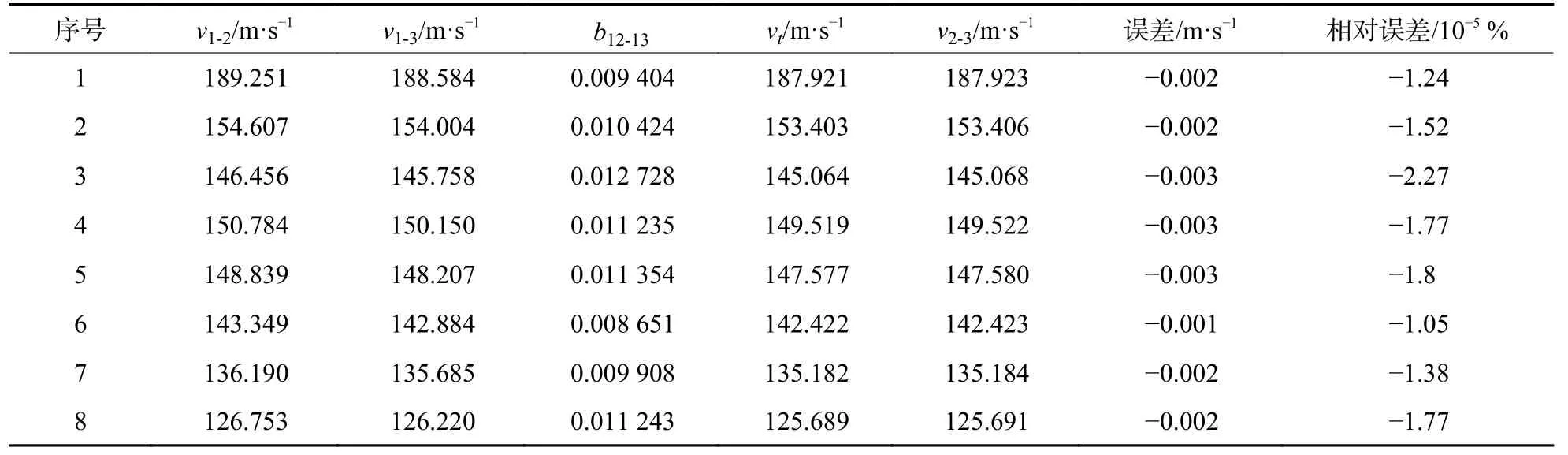
表4 气枪发射6 mm 钢珠测试数据Table 4 Test data of air gun shooting 6 mm steel ball

v1-2、v1-3、v2-3分别表示光幕1、2 之间、光幕1、3 之间以及光幕2、3 之间测速点的实测速度；b12-13表示通过v1-2、v1-3计算所得的参数B值；vt为使用v1-2和B值经过式（5）计算得到的v2-3测速点位置的瞬时速度；误差项为实测速度值v2-3与计算得到的同一位置的瞬时速度vt值之差；相对误差项为误差项除以v2-3的比值。

步枪试验测试时，4 个光幕的布放如图15 所示。将4 次实验中的B值和相对误差进行统计分析，如表6 所示。

表6 测试统计数据Table 6 Test statistics

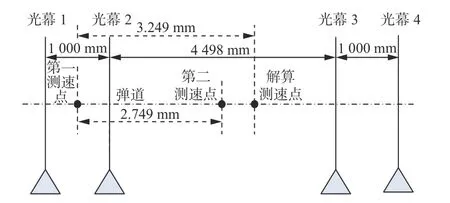
图15 步枪实验光幕布放示意图Fig.15 Schematic diagram of light curtain arrangement of rifle experiment

实弹实验均采用精度为0.1%的区截测速装置测量，而实验数据中速度相对误差均远小于0.1%，表明该模型的测试精度不低于所采用的区截测速装置的0.1%精度。在同一组实验中（同类的弹丸、同样的发射条件）B值标准差较小，而在不同组间B值均值差异较大。弹弓和气枪测试速度在0.8 倍音速以内，步枪的测试速度在1.2 倍音速以上，数据表明测试精度均高于0.1%，因此本文所提方法在速度低于0.8 倍音速和高于1.2 倍音速时均能够满足常规弹丸速度测试需求。

5 结论

提出了一种弹丸瞬时速度测量方法。通过采用双区截测速装置，得到2 个测速点速度，依据该速度值计算得到包含空气密度、弹丸最大横截面积、弹丸质量、弹丸阻力系数等参数信息的弹丸速度衰减系数B，使用B计算沿弹道方向距离第一测速点S处的弹丸瞬时速度，从而实现区截测试区域附近任意位置瞬时弹速高精度测量。通过理论仿真及对弹弓、气枪、步枪实弹实验，验证该方法具有较高的测量精度。该方法仅适用于速度在0.8倍音速以下或者1.2 倍音速以上的飞行弹丸，当弹丸速度在音速附近时由于速度衰减系数变化过快且成非线性，无法等效为常数，因此不适用于本文模型。另外，应用该方法能够改良炮口初始速度的测试方法，并且能有效提高测试精度。同时，使用B值能够计算得到飞行弹丸经过测试点后t时间的空间位置，从而实现弹丸空间坐标的高精度测量，提高使用六光幕阵列天幕立靶测量空间炸点坐标的测试精度。研究结论适用于不考虑重力，且弹丸为理想球形，或其迎风角度近似为零度的情况。