滞变阻尼对周期轨道结构垂向振动带隙特性影响

洪显 郭文杰 戴承欣

摘要：为探究滞变阻尼对周期轨道结构带隙的影响，以我国有砟轨道为例，基于能量泛函变分原理分析其带隙特征。通过将滞变阻尼效应引入钢轨、扣件和道床中，研究了周期性有砟轨道的频散特性随阻尼的变化情况。进一步地，研究了阻尼作用下轨道结构的振动传输特性。结果表明：无阻尼轨道结构的带隙范围与振动响应的衰减范围一致;钢轨阻尼很小且对轨道结构带隙几乎没有影响，在计算和预测振动时可以忽略;扣件的阻尼会略微增加轨道结构带隙，对带隙整体影响不大，但对于振动响应，扣件阻尼的耗散作用会增加150～500 Hz内振动衰减范围;道床阻尼增大会增加第一阶带隙范围，但会减小第二阶带隙范围，在振动响应中，增大道床阻尼能够使260 Hz内的钢轨振动均发生衰减。

关键词：滞变阻尼;周期结构;有砟轨道;带隙;传输特性

中图分类号：U213.2 文献标志码：A

本文引用格式：洪显，郭文杰，戴承欣. 滞变阻尼对周期轨道结构垂向振动带隙特性影响[J]. 华东交通大学学报，2023，40（1）：82-91.

Effect of Hysteresis Damping on Vertical Vibration Band Gap

Characteristics of Periodic Track Structure

Hong Xian，Guo Wenjie，Dai Chengxin

（School of Transportation Engineering， East China Jiaotong University， Nanchang 330013， China）

Abstract：In order to explore the effect of hysteresis damping on the band gap of periodic track structure， the ballasted track of was taken as an example， and the band gap characteristics were analyzed based on the energy functional variational principle. By introducing hysteretic damping effect into rails， fasteners and track bed， the variation of dispersion characteristics with damping of periodic ballasted track was studied. Furthermore， the vibration transmission characteristics of the track structure under the effect of damping were explored. The results show that the band gap range of the undamped track structure is consistent with the attenuation range of the vibration response; the rail damping is very small and has little effect on the band gap of the track structure， which can be ignored when calculating and predicting vibration; the damping of the fasteners slightly increases the track structural band gap and has little effect on the overall band gap， but for the vibration response， the dissipation effect of the fastener damping increases the vibration attenuation range within 150～500 Hz; the increase of the ballast bed damping increases the first-order band gap range， but it decreases the second-order bandgap range， in the vibration response， increasing the damping of the track bed can dampen the vibration of the rail within 260 Hz.

Key words： hysteresis damping; periodic structure; ballast track; band gap; transmission characteristics

Citation format：HONG X，GOU W J，DAI C X. Effect of hysteresis damping on vertical vibration band gap characteristics of periodic track structure[J]. Journal of East China Jiaotong University，2023，40（1）：82-91.

現代铁路大多都采用大型机械进行模块化施工，轨枕间距稳定，因而具有较强的周期性特征。以有砟轨道为例，周期性结构具有带隙特性，在禁带的频率范围内的弹性波无法沿结构传播，从而使该结构振动衰减[1-2]。研究周期轨道的带隙特性，掌握其内弹性波的传播机理，对实现轨道结构振动的精准控制具有重要的工程意义。

对于周期性结构的研究，Sheng[3-4]提出了一种基于傅里叶变换，计算周期轨道结构在移动或静止简谐荷载作用下的响应计算方法。Wang等[5-7]基于传递矩阵法和Bloch理论求出了周期轨道结构的带隙，发现Bragg带隙和局部共振带隙在周期轨道结构中共存。易强等[8]结合传递矩阵法与Bloch定理计算出了有砟轨道的带隙，同时运用波叠加和功率流法分析了轨道结构的动力响应及轨道内弹性波的传播特性。

在上述关于周期轨道结构的带隙研究中，很少考虑阻尼效应，但在实际的铁路结构中，由于施工和材料本身的因素，无阻尼情况是不存在的。并且，在一些研究中可以了解到，阻尼对铁路结构各项特性都有一定影响。

谷爱军等[9]通过对北京地铁钢轨异常波磨的研究，发现扣件阻尼能够影响钢轨的波磨形成。张迅等[10]基于车-线-桥耦合振动理论和声学边界元，分析了扣件阻尼对铁路简支箱梁结构声辐射特性的影响规律。方锐等[11]通过建立轨道结构的有限元模型，研究了钢轨、轨下垫层和道床的阻尼损耗因子的变化对钢轨和轨枕振动特性有着不同范围和不同程度的影响。Iqbal等[12]研究了刚性轨枕支撑的周期性轨道的横向和竖向弯曲波传播，并研究了钢轨和谐振器的阻尼对带隙特性的影响。

为探究阻尼变化对轨道结构带隙特性的影响，本文以有砟轨道为研究对象，基于能量泛函变分法[13]，引入滞变阻尼效应，研究其带隙特征。滞变阻尼又称为复阻尼，通常是通过材料试验得出的，比较符合实际工程状况[14]，而且滞变阻尼是通过阻尼损耗因子将阻尼复化到刚度中，十分契合能量法的求解。本文首先计算无阻尼的周期性有砟轨道带隙，并与文献和有限元模型进行对比，证明该方法的正确性。之后分别设置钢轨、扣件和道床滞变阻尼，对比分析阻尼变化对结构带隙的影响。为进一步验证阻尼对周期轨道结构的带隙特性影响，本文结合有限长轨道结构的振动传输特性来分析阻尼影响。

1 频散特性分析

如图1所示，取轨道结构的一个特征周期建立垂向振动分析模型：钢轨考虑为Timoshenko梁单元，轨枕考虑为质量块，扣件系统和碎石道床视为弹簧-阻尼单元。在特征周期中以钢轨最左端建立笛卡尔坐标系xRORzR， 其中zR和zS分别为钢轨和轨枕的垂向位移;特征周期长度为轨枕间距，即l;扣件的垂向刚度为kF，阻尼为cF;道床的垂向刚度为kB，阻尼为cB。传统有砟轨道结构参数[4，8，15]见表1。

1.1 带隙计算理论

1.1.1 钢轨的能量泛函

钢轨的能量包括应变能和动能。基于Bloch理论和平面波级数，可构造满足周期边界条件的钢轨位移场函数

zR（xR）=eikxR

zj expi

θR（xR）=eikxR

θj expi

（1）

式中：zR和θR分别为钢轨的垂向位移和截面转角;i为虚数单位;k为Bloch波数;xR为沿钢轨轴向的坐标;zj和θj为未知系数。

基于Timoshenko梁理论，可得钢轨的应变能和动能

UR=

2dxR+θR

-2dxR（2）

VR=ρRΑR zR2dxR+ρRIR θR2dxR（3）

式中：UR和VR分别为钢轨的应变能和动能;ER，IR，kR，GR，AR和ρR分别为钢轨的弹性模量，截面惯性矩，剪切系数，剪切模量，横截面积和质量密度;ω为结构固有圆频率。由于考虑了滞变阻尼的效应，故此处的钢轨弹性模量为：ER=ER0（1+iηR），ER0為初始弹性模量，ηR为钢轨的阻尼损耗因子，取值见表1。

1.1.2 扣件的能量泛函

扣件的能量为其弹性势能，其表达式为

UF=kF[zR（xR=l/2）-zS]2（4）

式中：zR（xR=l/2）表示钢轨在扣件处的垂向位移;kF为考虑阻尼后的扣件刚度：kF=kF0（1+iηF）， kF0为初始扣件刚度，ηF为扣件的阻尼损耗因子，取值见表1。

1.1.3 轨枕的能量泛函

由于轨枕被考虑为质量块，其能量应为动能，即

VS=mSzS2（5）

式中：mS为轨枕的质量。

1.1.4 道床的能量泛函

道床的能量为其弹性势能，其表达式为

UB=kB zB2（6）

式中：kB为考虑阻尼后的道床刚度：kB=kB0（1+iηB），

kB0为初始扣件刚度，ηB为扣件的阻尼损耗因子，取值见表1。

1.1.5 系统的总能量泛函与特征方程

系统的总能量泛函Π为总应变能与总动能之差，即

Π=UR+UF+UB-VR-VS（7）

基于Hamilton原理对总能量泛函变分（对Π中未知量zj，θj和zS求极值），可得到周期有砟轨道中弯曲波传播的特征方程

（Ktot-ω2Mtot）Q=O（8）

式中：Ktot和Mtot分别为总刚度矩阵和总质量矩阵;Q为未知系数向量;O为0距阵。在第一 Brillouin区内对上式求解，可到的周期有砟轨道中弯曲波的带隙特性。

1.2 带隙的准确性验证

1.2.1 无阻尼带隙

为验证能量法求解带隙的准确性，将轨道结构的阻尼损耗因子ηR，ηF和ηB设为0，可得到无阻尼带隙特性，再与文献[8]的结果进行对比，见图2和表2。根据文献[16]，轨道结构中的弯曲波可分为两类，即近场波（文献[16]中第1类弯曲波）和弥散波（文献[16]中第2类弯曲波）。由于近场波波数虚部始终不为0，故其在全频段范围内均是带隙，而弥散波既能传播又能衰减（如图2（b）所示，0～1 500 Hz范围内存在3条带隙）。显然，轨道结构中弯曲波的带隙特性取决于弥散波;因此，本文主要研究的是弥散波的带隙特性。

由图2和表2可知，基于能量法所求得的周期性有砟轨道中弯曲波的带隙范围及频散曲线与文献[8]结果基本一致，这可以证明了能量法求解带隙特性的准确性。

1.2.2 有阻尼带隙

考虑轨道结构的损耗因子ηR=0.01、ηF=0.25和ηB=1.0，可得到有阻尼带隙特性，再与有限元结果进行对比验证，见表3。

从表3中可以看到两种方法的频率的实部与虚部基本相同，由此可证用能量法求解含滞变阻尼的带隙也是可行的。

1.3 阻尼对带隙的影响分析

1.3.1 钢轨阻尼

60 kg/m钢轨是中国铁路的主轨型，也是铺设最广的钢轨。其结构形式和材料属性固定，因此其阻尼损耗因子ηR一般也是定值（通常取ηR=0.01）。为研究钢轨滞变阻尼的影响，这里设置ηB=ηF= 0，ηR从0变化到0.02，有砟轨道带隙变化如图3。

由图4可以明显看出，在1 500 Hz内的3条带隙中，阻尼的增加几乎不会影响带隙宽度。这与钢轨本身的阻尼很小有关;因此在计算时，可以不设置有砟轨道的阻尼。从表4中看出含有滞变阻尼钢轨的带隙的虚数部分（阻尼衰减项）与阻尼损耗因子呈线性变化。

1.3.2 扣件阻尼

扣件的种类很多，不同的扣件的刚度和阻尼也不一样，而在。因而探究清楚扣件阻尼对周期带隙的影响，才能确定扣件阻尼的取舍。设置ηR=ηB=0，ηF从0变化到0.25，有砟轨道带隙变化如图4和表5。

扣件阻尼仅对有砟轨道的第1阶与第2阶带隙有轻微影响，随着阻尼的增加，第1阶带隙和第2阶带隙的起始频率和截止频率在略微增大。阻尼损耗因子从0增加到0.25，第1阶带隙宽度增大0.5 Hz，第2阶带隙宽度增大1.2 Hz且带隙频率位置略微上移。总体上，扣件阻尼的变化对周期有砟轨道的带隙特性影响不大，在带隙计算中扣件阻尼损耗因子可不予考虑。而且随阻尼损耗因子增加n倍，虚部的值也大致呈n倍增加。由此可以看出扣件阻尼的衰减作用是和扣件阻尼损耗因子大小是有线性关系的。

1.3.3 道床阻尼

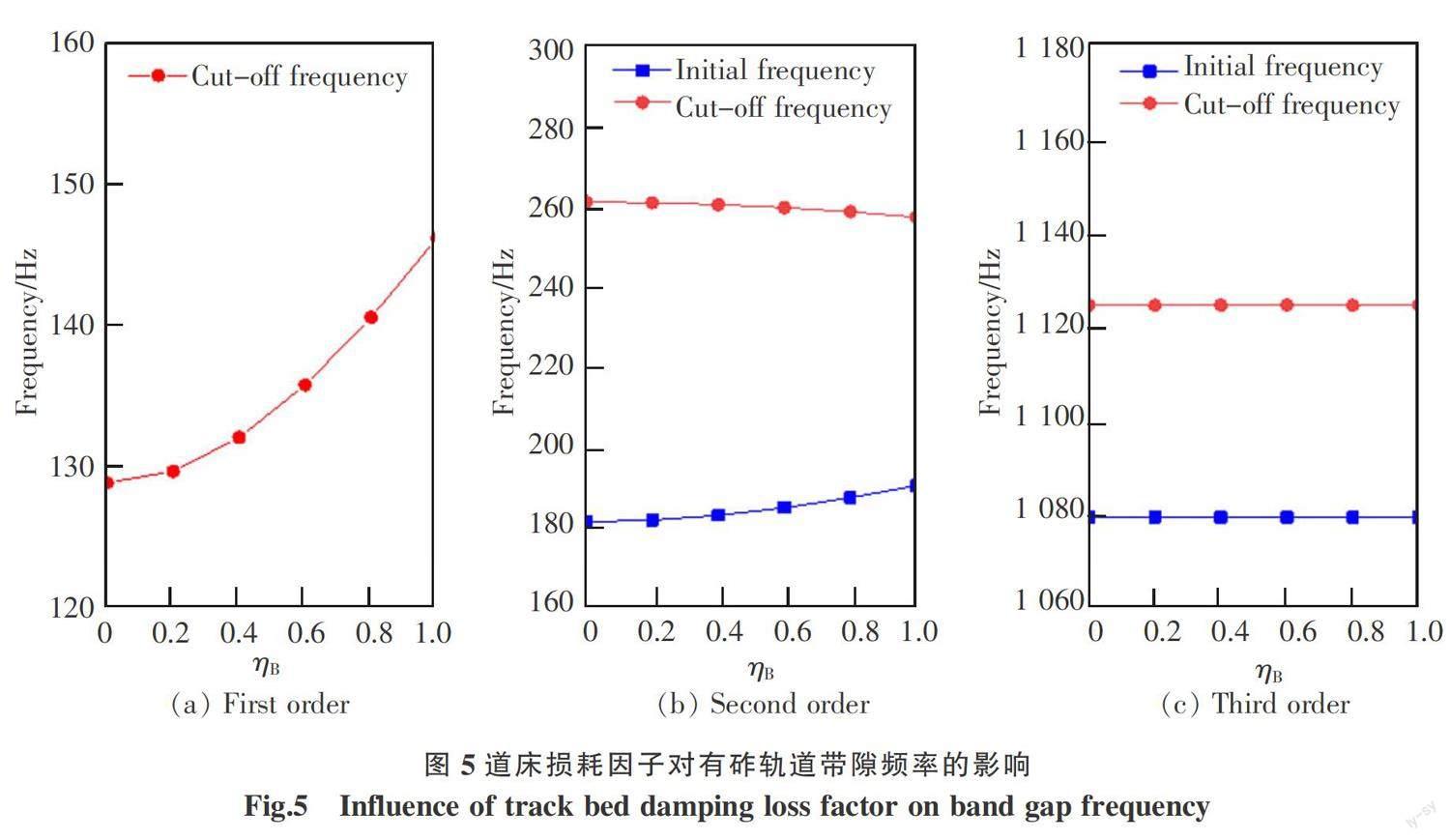
有砟轨道的道床阻尼受道砟的压实度，级配类型等影响[17]，并且对于经过城市有砟轨道，有一定的降低环境振动的需求，需要增加道床的阻尼。再者聚氨酯固化道床[18]也在被研究，具有一定的发展前景与应用，其阻尼相较一般道床更大。故而道床阻尼有较大变化幅度的;设置ηR=ηF= 0，ηB从0变化到1.0，有砟轨道带隙变化如图5和表6。

道床阻尼对有砟轨道的第1阶与第2阶带隙有明显影响，对第3阶带隙几乎无影响。道床阻尼损耗因子从0增加到1，第1阶带隙宽度增加了17.5 Hz，且随着阻尼的增加，宽度增加的幅度也在增加，第2阶带隙起始频率增大，截止频率降低，带隙宽度减小12.8 Hz。总体上，道床阻尼的取值对周期有砟轨道的中低频带隙特性影响显著，因此在带隙计算中道床阻尼损耗因子应予以考虑。

2 传输特性分析

周期结构的带隙特性表征方法除无限周期结构的能带之外，主要还有有限周期结构的传输特性[19]。为进一步理解周期轨道结构的带隙特性，本节拟结合有限长轨道结构的振动传输特性来对带隙特性进行解释。结构的振动传输特性是指不同频率的入射弹性波在该结构中的传播能力，通常是用激励端的频响函数和响应端的频响函数的比值来表征。

2.1 计算原理

2.1.1 计算模型

振动传输特性的求解思路与上文中的帶隙求解理论基本相似，但需要引入外荷载（本文为点荷载）并将其转化为外力做功，再结合功能关系求解结构的振动响应。有限长周期轨道结构在固定点谐荷载作用下的振动传输特性计算模型见图6。如图6所示，加载端位于模型的首端（周期1的首端）;响应端位于模型的尾端（周期n的尾端）;固定点谐荷载为F（t）F（，t）=F0 eit;F0为荷载幅值，取1 N;为激振频率），作用于周期1中的钢轨起点，方向垂直向下。

2.1.2 理论推导

下面将介绍基于能量泛函变分原理求解有砟轨道结构的振动响应，有砟轨道的响应求解可依此推导出。

1） 钢轨能量泛函。

由于图7中模型为有限长结构，故选用改进Fourier级数构造钢轨的位移场函数

zB（xB）=

zj λj（xB）eit=eitλ（xB）H1

θB（xB）=

θj  λj（xB）eit=eitλ（xB）H2（9）

式中：λ（xB）是梁的位移形函数行向量，形函数采用改进Fourier级数，见式（1）;xB取值为[0，l]，l0为轨道结构长度;N1形函数项数;H1和H2为未知系数列向量。

一般情况下，结构在点谐荷载的作用下做受迫振动，其角频率与激振力的角频率相同，而其中各点位移的振幅和它与激振力间的相位差只决定于系统本身特性和力的性质，与运动初始条件无关。因此，只需求解得到位移幅值和相位差即可得到结构在受迫振动位移的稳态解。在本文方法中，只需求得各未知系数列向量即可得到每个点处的位移。为了方便后续的理论公式推导，简化推导过程，在之后的公式中都略去而仅保留位移展开式中的时间项eit。

将式（9）代入式（2）、式（3），可得到受迫振动下梁的应变能和动能

UB=

dxB+θB

-dxB

=HTMBH（10）

VB=ρBΑB zB2dxB+ρBIB θB2dxB

=HTMBH（11）

2） 扣件弹性势能。

UF1=kF zB xB=

+n-1l0-zS，n（12）

式中：N为选取的周期数，在本文中取N=50。

3） 轨枕动能。

VS=mSzS，n2（13）

4） 道床弹性势能。

UD=kDzS，n2（14）

5） 总能量泛函。

系统的能量泛函为

Π=UB+UF1+UD-（VB-VS）

UB+UF2+UP+UP，B+UCA-（VB+VP）（15）

外力做功为

W=F0 eit·zB（xB=0）dt

=F0 ·λ（xB=0）Η11=Η（1，10）=F（16）

总能量泛函为

Ψ=Π-W（17）

6） 振动响应计算。

对总能量泛函Ψ未知系数求一阶偏导，可得振动控制方程：

Η（1，10）=（K-2M）-1F（18）

将式（18）代入式（9）即可得到在某一任意频率的点荷载F作用下，激励点处的位移幅值（频响函数）和响应点的位移幅值

zB1（xB=0）=λ（xB=0）·H11

zB10（xB=l0）=λ（xB=l0）·H110（19）

进一步地，可得有砟轨道结构的振动位移传递率rT

rT=20log10

dB（20）

2.2 振动传递率分析

计算振动响应的各个参数取值见表1，首先取鋼轨、扣件和道床的阻尼损耗因子均为0，并将得到结果与之前计算的带隙结果进行对比，见图7和表7。

由图8和表4的对比结果可以看出位移传递率为负的频率带是和轨道带隙是大致是重合的，由此可见在周期有砟轨道的带隙范围内，弹性波会产生衰减，而这部分的衰减全是由带隙造成的。同时，这也证明了2.1中的振动响应的理论计算的正确性。

2.3 阻尼对传递率的影响分析

2.3.1 钢轨阻尼

其他参数不变，ηR从0变化到0.02，有砟轨道振动响应变化如图8。

在图8中，不同阻尼损耗因子的传递率变化曲线几乎是重合的。在数值上，如在第一段衰减区，钢轨损耗因子从0到0.01，0.02;衰减的最大频率从129 Hz到130，131 Hz。钢轨损耗因子的变化对钢轨传递率几乎是没有影响的，即设不设置钢轨滞变阻尼，对结构整体几乎没有影响。这与前面带隙所得出的结论一致。

2.3.2 扣件阻尼

其他参数不变，ηF从0变化到0.25，有砟轨道振动响应变化如图9。

在第1段的衰减频率范围内，扣件阻尼的从0到0.15再到0.25，衰减的范围从129 Hz到136 Hz再到139 Hz，相对来说变化不大。在第2段衰减频率范围内（158～500 Hz），无阻尼的扣件振动会剧烈衰减，并在260 Hz之后就不再衰减，增大阻尼后，衰减幅度下降，衰减的起始频率会下降同时衰减的频率范围会增大。扣件滞变阻尼从0增加到0.25，衰减的最大频率从260 Hz，增加到500 Hz仍有少量衰减。而在前文中，扣件在第2阶的带隙增加仅有1.2 Hz，故造成衰减扩大的主要原因是阻尼本身导致的能量耗散。而在pinned-pinned频率（1 080 Hz）附近，扣件的阻尼对振动响应没太大影响。可以看出，扣件阻尼主要对该模型的第2阶传递率有较大影响。

2.3.3 道床阻尼

其他参数不变，ηB从0变化到1.0，有砟轨道振动响应变化如图10。

无道床阻尼时，结构在129～181 Hz内会有一段不衰减的频率，而随着阻尼损耗因子的增加，这段不衰减的频段会逐渐消失，在这频段的振动衰减幅度也会增加，而这个“峰值”会随着阻尼损耗因子的增加，频率也会向略微后移。在表5中可以看到道床的阻尼损耗因子从0增加到1，其带隙宽度从128.74 Hz增加到146.25 Hz。在181～260 Hz频率范围内，道床阻尼的增加会使得衰减的幅度降低，但会略微的增加衰减的范围，相比扣件阻尼导致的衰减范围要小很多，这说明该部分的衰减与第2阶带隙的宽度变小有关。

3 结论

1） 钢轨滞变阻尼很小且稳定，而且从带隙和振动响应的计算结果也可以看出钢轨的滞变阻尼对结构整体几乎没有影响，故而在计算和预测中可以不考虑。

2） 扣件阻尼对第1段带隙和第3段带隙的影响可以忽略不计。扣件阻尼的增加会略微增加第2阶带隙宽度，阻尼损耗因子为0.25的扣件比无阻尼扣件增加1.2 Hz且带隙频率位置略微上移。而阻尼本身的能量耗散作用会让振动响应的第2段衰减范围大幅度增加。

3） 有砟轨道道床的阻尼对第1阶带隙的影响较大，随着道床阻尼的增加，第1阶带隙宽度也会增加。道床阻尼损耗因子从0增加到0.25时，第1阶带隙宽度增加了17.5 Hz，第2阶带隙宽度减小12.8 Hz。而且因为第1阶带隙宽度的增大，并在阻尼的在振动响应表现为低频的振动都会发生衰减。因而在计算和预测中应该考虑道床的滞变阻尼影响。

4） 不论钢轨阻尼、扣件阻尼和道床阻尼，对结构的pinned-pinned处的带隙几乎没有影响，在该处的振动响应的衰减范围也没有影响，其衰减的幅度也没有太大变化。

参考文献：

[1] ESVELD C. Modern railway track[M]. Zaltbommel：MRT Productions，2001.

[2] 冯青松，梁玉雄，陆建飞. 基于声子晶体理论的轨道交通减振降噪研究综述[J]. 华东交通大学学报，2021，38（4）：54-63.

FENG Q S，LIANG Y X，LU J F. Review on railway vibration and noise reduction based on phononic crystal theory[J]. Journal of East China Jiaotong University，2021，38（4）：54-63.

[3] SHENG X. Generalization of the Fourier transform-based method for calculating the response of a periodic railway track subject to a moving harmonic load[J]. Journal of Modern Transportation，2015，23（1）：12-29.

[4] SHENG X，JONES C J C，THOMPSON D J. Responses of infinite periodic structures to moving or stationary harmonic loads[J]. Journal of Sound and Vibration，2005，282（1/2）：125-149.

[5] 王平，易强，赵才友，等. 基于局域共振机理的周期性轨道结构弹性波控制[J]. 中南大学学报，2018，25（12）：3062-3074.

WANG P，YI Q，ZHAO C，et al. Wave propagation control in periodic track structure through local resonance mechanism[J]. Journal of Central South University，2018，25（12）：3062-3074.

[6] WANG P，YI Q，ZHAO C Y，et al. Wave propagation in periodic track structures：band-gap behaviours and formation mechanisms[J]. Archive of Applied Mechanics，2017，87（3）：503-519.

[7] WANG P，YI Q，ZHAO C Y，et al. Elastic wave propagation characteristics of periodic track structure in high-speed

railway[J]. Journal of Vibration and Control，2019，25（3）：517-528.

[8] 易強，王平，赵才友，等. 有砟轨道结构弹性波传播特性研究[J]. 铁道学报，2019，41（6）：137-145.

YI Q，WANG P，ZHAO C Y，et al. Study on elastic wave propagation properties of ballast track structure[J]. Journal of the China Railway Society，2019，41（6）：137-145.

[9] 谷爱军，刘维宁，张厚贵，等. 地铁扣件刚度和阻尼对钢轨异常波磨的影响[J]. 都市快轨交通，2011，24（3）：17-21.

GU A J，ZHANG W N，ZHANG G H，et al. Impact of rail fastenings′ stiffness and damping on abnormal rail corrugation[J]. Urban Rapid Rail Transit，2011，24（3）：17-21.

[10] 张迅，苏斌，李小珍. 扣件刚度与阻尼对铁路箱梁车致振动噪声的影响研究[J]. 振动与冲击，2015，34（15）：150-155.

ZHANG X，SU B，LI X Z. Effects of fastener stiffness and damping on structure-borne noise of railway box-girders[J]. Journal of Vibration and Shock，2015，34（15）：150-155.

[11] 冯青松，杨舟，郭文杰，等. 周期离散支承钢轨垂向振动带隙特性分析[J].中国科学：技术科学，2020，50（12）：1563-1576.

FENG Q S，YANG Z，GUO W J，et al. Analysis of vertical vibration band gap characteristics of periodic discrete support rail[J]. Science Sin Technoloty（in Chinese），2020，50（12）：1563-1576.

[12] IQBAL M，KUMAR A，MURUGAN J M，et al. Flexural band gaps and vibration control of a periodic railway track[J]. Scientific Reports，2021，11（1）：1-13.

[13] 郭文杰. 任意形状Mindlin板的弯曲自振特性分析[J]. 华东交通大学学报，2019，36（5）：22-32.

GUO W J. Free vibration analysis of mindlin plates with arbitrary shapes[J]. Journal of East China Jiaotong University，2019，36（5）：22-32.

[14] 田坤，李鹏，王元丰. 结构等效复阻尼模型对钢梁及钢框架结构动力响应影响分析[J]. 振动与冲击，2008，27（7）：118-121.

TIAN K，LI P，WANG Y F. Analysis of dynamic response of steel beam and steel frame structures with structural equivalent complex damping model[J]. Journal of Vibration and Shock，2008，27（7）：118-121.

[15] 汪瑋. 基于振动理论的铁路无缝线路温度力检测方式研究[D]. 南昌：华东交通大学，2017.

WANG W. Study on vibration characteristics of CWR track structure with axial temperature force[D]. Nanchang：East

China Jiaotong University，2017.

[16] CREMER L，HECKI M，PETERSSON B A T. Structure-borne sound[M]. Berlin，Heidelberg：Springer，2005.

[17] 刘卫星，王午生. 铁路碎石道床动刚度与阻尼的试验研究[J]. 铁道学报，2002，24（6）：99-104.

LIU W X，WANG W S. Study on dynamic stiffness and damp measurement of railway crushed stone ballast[J]. Journal of the China Railway Society，2002，24（6）：99-104.

[18] 冯仲伟，许良善，郄录朝，等. 大西高速铁路聚氨酯固化道床技术应用[J]. 中国铁路，2021（6）：16-20.

FENG Z W，XU L S，QIE L C，et al. Application of polyurethane solidified ballast bed technology in Datong-Xi′an HSR[J]. China Railway，2021（6）：16-20.

[19] 温激鸿，郁殿龙，赵宏刚，等. 人工周期结构中弹性波的传播：振动与声学特性[M]. 北京：科学出版社，2015.

WEN J H，YU D L，ZHAO H G，et al. Propagation of elastic waves in artificial periodic structures：vibration and acoustic characteristics[M]. Beijing：The Science Publishing Company，2015.